培养学生规范数学答题的途径分析①

孙居国

(南京师范大学附属中学 210003)

不少一线的高中数学老师，总是抱怨学生的解题不规范.学生自己也很苦恼，很多明明会做的题目在考试中总是做不对或做不全对，特别是在每年的高考后，绝大部分学生的实际数学得分比自己估分少了不少，也就是说高中数学解题不规范的现象普通存在.针对这一现象，本文谈谈培养学生规范数学答题的途径.

1 理解答题的教育价值，树立学生规范数学答题的观念

能够用精确、简约的数学语言去表达自己的想法和思考过程是数学素养的特征之一.而高中数学答题的本质也正是如此.而在解答题的过程中，往往大部分学生重视的是“对数学题的想法和思考”，这是片面的，而答题的核心教育价值是“能够用精确、简约的数学语言去表达的过程”.

从这一教育价值出发，要答好题，须要对“想法和思考”进行再加工，因此答题是一个比解题更加全面的过程.要求学生的规范解题，也就是提升学生的数学综合能力和素养的过程.

解数学题是要遵循严格的规则，从确定的条件出发，得出正确的结论.解答数学题是一个创作的过程，创作的一个重要特征是“构思”，不光有正确的思想，还要有完整的结构，通俗易懂.因此，要答好题，在思想上要重视，在方法上要引导，在实践中要严格，通过长时间的坚持从而形成规范的答题习惯.

规范答题要求逻辑推理严密完整，三段论中“大前提，小前提，结论”缺一不可，在体现数学思维的关键处给出充分的关注，要保证解题和答题的过程中科学性与艺术性的统一，体现出专业化的水平.例在很多情况下，我们寻找解题思路用的是分析法，而书写答题过程则用的是综合法，要提高规范的意识，目标明确，反复实践，形成习惯，反思总结，螺旋上升，达到自动化的水平.通过适量的解题实践积累解答题的经验，形成规范答题的感觉和相对成熟的模式.

要让学生充分认识到答题过程是对“想法和思考”的再加工，答题是需要学生明白为什么这样答题的，是要老师示范、引导、鞭策、激励的，不是全靠学生自然形成的，也就是说答题规范还要需要通过教学活动来达成的，要运用这一价值观念作为答题教学的重要依据.

2 提升数学的认知水平，培养学生规范数学答题的能力

一个数学题目总是承载着数学的知识和方法，体现着数学的本质和思想.通过解题加深对高中数学中的理解，也就是理解数学的概念、知识、方法.从而提升数学认知水平.如果学生的数学知识不完善，概念定理规则不准确，则解题就不可能规范.因此通过提升数学认知水平，是培养学生规范数学答题的能力的重要途径之一.

例如，一次高三复习课上遇到这样问题：

已知圆C：(x-1)2+(y-2)2=9，直线l：y=kx+5.若直线l与圆C交于A，B两点，求△ABC面积的最大值.

解法一：设∠ACB=θ，

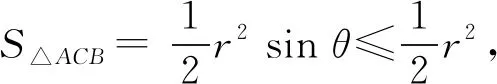
解法二：设圆心C到直线l的距离为d，

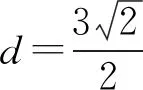
解法三：设圆心C到直线l的距离为d，

因为直线与圆有两个交点，

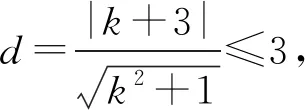
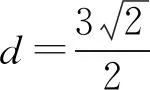
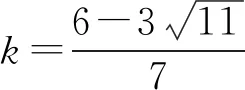
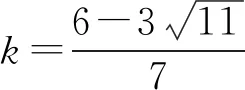
从表面上看，这几种解法答案是一样的，好像全是正确的，前2种解法比较简单，解法三特别麻烦，那么怎样评价这几种解法呢？问题的焦点是：是不是一定要说“当k为何值时”，△ABC面积的最大值为多少？作为教师我们怎么评判？不妨问一下：什么叫最大值？它的定义是什么？

回到问题的本源，获得解决问题的依据，提升学生的数学认知水平，从而提高学生的规范数学答题的能力.

苏教版必修一中如是说：

一般地，设y=f(x)的定义域为A. 如果存在x0∈A，使得对于任意的x∈A，都有f(x)≤f(x0)，那么称f(x0)为y=f(x)的最大值，记为ymax=f(x0)；如果存在x0∈A，使得对于任意的x∈A，都有f(x)≥f(x0)，那么称f(x0)为y=f(x)的最小值，记为ymin=f(x0) .

接着课本例题是求下列函数的最小值：

(1)y=x2-2x；

解：(1)因为y=x2-2x=(x-1)2-1≥-1，且当x=1时y=-1，所以函数取得最小值-1，即ymin=-1.

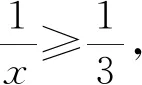
有不少教师认为，函数的最大值和最小值，不像函数单调性、奇偶性定义那样抽象，需要分析过程，详细讲解，反思练习，而只要从字面理解即可，而对于此例题，则是更简单，只要学生口答一下结果就行了，有的甚至“滑过”不讲，直接讲解高难度的例题.其实这种做法是对数学理解不够，更谈不上提高学生的数学认识水平.

此例题是在定义了函数最大(小)值的定义后给出的，目的不是要结果，而是通过此题，加深对概念定义准确、全面的理解，而不是直观字面上的理解，也是学生要用数学的定义等规则去规范逻辑化的解题，也说是说一个新的数学对象出现后，通常通过特殊化的例子达到对概念的理解.定义中最大值或最小值为f(x0)，也就是要完整说清楚：当x=x0，函数f(x)取得最大值或最小值为f(x0)，不但定义中是这样的，并且例题中也是给出了示范.

因此必须写 “当k为何值时”，△ABC面积的最大值为多少.这是数学定义的要求.高中数学概念是有限的，而数学题目是无限的，我们可以减少一点题目而多重视一点概念，使得学生对数学概念定义掌握得更加深刻、精确、全面，重视课本中的概念定义和例题、习题.让学生自觉地用定义去思考问题，从而提升了学生的数学认知水平，并成为以后解题的范例，也提高了学生的规范数学答题的能力.

3 揭示解题的思维过程，优化学生规范数学答题的结构

一个数学题的解答过程，要有良好的规范的答题结构.从其形态来看是一种外显的、静态的、物化了的东西，而背后隐藏了知识联系的动态思维过程.在解题教学过程中，要不断再现隐藏在题目背后的知识的内在的联系，在此基础上建构合理的解题结构.如果解题教学脱离学生实际，忽视过程，被告知获得只是灌输加记忆，没有思维价值可言，更不能形成规范的答题能力.

解题不能脱离学生的思维起点，不能置学生的心理、思维过程于不顾，强制学生按照教师提出的方法、途径去思考和解决问题，而是要充分暴露学生解题的思维过程.学生经历了曲折的思维过程，才能获得过程的体验，这种获得与那种被告知结果的获得有本质的不同，这种获得是思维建构的过程，学生的思维获得了发展，解答题的结构自然得到优化.

例如，一个关于向量命题的证明的教学过程如下：

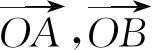
求证：A，B，C三点共线的充要条件是λ+μ=1．

学生的解答如下：

先证充分性.若λ+μ=1，

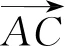
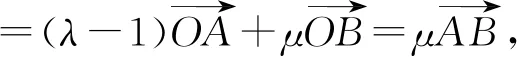
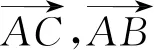
再证必要性．若A，B，C三点共线，

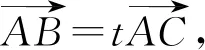
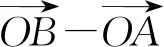
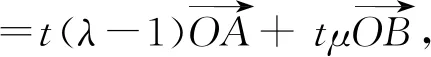
所以t(λ-1) =1，tμ= -1，

所以t(λ-1+μ) = 0，所以λ+μ=1.

所以A，B，C三点共线的充要条件是λ+μ=1.

从表象上来看，这一证明很规范，该生在测试中获得满分，估计是老师在批阅试题时，忽视了过程，仅看了结果，没有深入了解学生解题的思维过程，特别是其中的一些细节，以致许多答题不规范的现象被掩盖了.

不妨将解题过程在黑板上或电子屏幕上呈现出来，让学生反复观察，认真体会每一步过程，师生共同探讨如下：

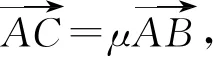
这一步是不精确的.

向量共线定理：如果有一个实数λ，使得b=λa(a≠0)，那么b与a是共线向量；反之，b与a(a≠0)是共线向量，那么有且仅有一个实数λ，使b=λa．

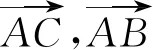
向量共线包括线段平行与共线，与三点共线是不一样的，因此须加条件线段AC，AB共端点.

所以t(λ-1) =1，tμ= -1

为什么？

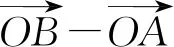
通过上述的过程分析，说明学生由于对向量基本定理和向量共线定理的掌握不完整，因而解题不规范，通过师生的共同探讨过程，学生加深了对向量共线定理，平面向量基本定理等内容的认识，使得解题的结构获得优化.然后师生再共同讨论：本题的解题结构是怎样的？先证充分性还是必要性？有哪此关键步骤？每一步要注意什么问题？

教师在课堂上往往是解题方法、解题过程三言两语一带而过，不给学生理解的时间和表达自己理解的机会，也不组织学生讨论，而是让学生花费大量的时间进行重复性的强化训练，学生就失去了大量的提升规范答题的机会.上述师生答题过程的展示，反省解题的过程和答题的规范，可以使学生对自己的错误观念进行深刻的理性认识，在剖析产生错误的前因后果的基础上，产生正确的认识，从而实现认识上的知其然又知其所以然.

4 呈现丰富的示范例证，启迪学生规范数学答题的智慧

对学生解答题的呈现是课堂教学的重要资源，是书本上所没有的，是第一手的资料，是丰富的宝藏.因为教学内容是来源于学生的思考成果，更接近学生实际，更容易被学生接受.这样，学生解题的视野更宽广，思维会更加深刻，得到的结论更为丰富而严谨.因此，学生获得的不只是一个公式、一种方法、一个结论，而是一种主动学习、深入研究的能力，一种多向思维、合作交流的能力，一种敢于质疑、勇于创新的科学研究精神，从中启迪学生规范数学答题的智慧.

例如在一次练习中，同学对如下问题的三种解法展示如下：

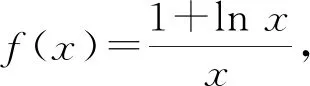
当00，

当x>1时，f′(x)<0，

所以f(x)在(0，1)上单调递增，

在(1，+∞)上单调递减，

当x=1时，f(x)取得极大值1.

令g(x)=x2-2x+k，

则g(x)的最小值为g(1)=k-1.

要使f(x)=g(x)有实数解，则k-1≤1，即k≤2，

所以实数k的取值范围为(-∞，2] .

解法二：

由f(x)=x2-2x+k，

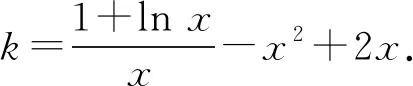
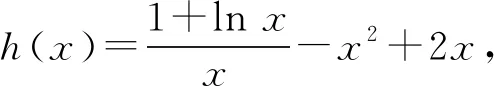
当00，

当x>1时，h′(x)<0，

所以h(x)在(0，1)上单调递增，

在(1，+∞)上单调递减，

当x=1时，h(x)取得极大值2，

所以实数k的取值范围为(-∞，2] .

当00，

当x>1时，g′(x)<0，

所以g(x)在(0，1)上单调递增，

在(1，+∞)上单调递减，

当x=1时，g(1)取得极大值2-k.

当k>2时，最大值g(1)<0，

函数g(x)的不存在零点，不符合条件；

当k=2时，1是函数g(x)的一个零点，符合条件；

当k<2时，g(1)=2-k>0，

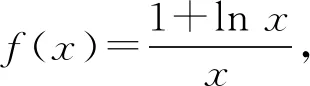
当00，

当x>1时，f′(x)<0，

所以f(x)在(0，1)上单调递增，

在(1，+∞)上单调递减，

当x=1时，f(x)取得极大值1，

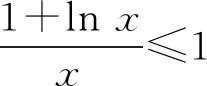
≤1-x2+2x-k=-(x-1)2+2-k，

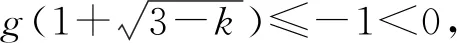
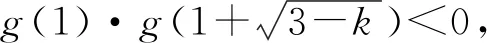
又因为函数g(x)在(0，+∞)的图像是不间断的，

所以函数g(x)在(0，+∞)存在零点，符合条件.

综上，实数k的取值范围为(-∞，2] .

上述不同解法体现了同一数学问题可以从不同方面加以表征，有的重视言语化，有的重视视角化；有的重视模式，相互既有联系又有区别.

让学生仔细观察三种方法，比较解答过程，说出各种解法的优势和不足.

解法一借助图形的直观性，根据两个函数图像的交点，从而得到关于k的取值范围，优点直观简洁，充分体现了数形结合的思想.可以作为填空或选择题的解法，但作为解答题的答题过程，则是以图形的直观性取代了推理的过程，是不准确不完善的.

解法二是通过构造函数，将动态函数问题转化为静态函数问题，从而通过求函数的值域获得k的取值范围.这种解法是函数的值域来的突然，要有正确的推理过程，k的取值范围是函数的值域与方程f(x)=x2-2x+k有实数解还不一致，还缺少一步论证过程，因此严谨性还不够.

解法三则是比较长，但规范严谨，每步都有依据，把方程解的问题转化为函数零点问题.根据零点存在定理，从而得出k的取值范围.这一种解法体现了方程解的问题转化为函数零点问题的这一基本思想，反映了数学的本质.这种解法体现了题目与重要的数学概念和性质相关，解题方法自然，具有发展性，表述流畅且好懂等特点.从解题的方法来讲，具有自然多样，还具有发展性，是规范解题的示范.

通过上述比较分析，可以帮助学生克服一些先入为主的观念，只有通过不断的反思和比较，从不同的解法中引出深刻的思想和全面的认识.根据题目的具体需要给出规范的答题过程.

总之，培养学生规范数学答题的途径不是一招一式就能成就的，要师生共同持之以恒，反复实践.教师要讲好标准，以课本为依据，以高考考试说明中的解答为示范，规范解好每一题.学生要正确认识解题的价值，相互学习，借鉴比较，不断的对自已的答题过程进行反思和总结，从而使自己规范答题的能力得到提升.做到能够用精确、简约的数学语言去表达自己对数学的想法和思考的过程.