余弦级数的敛散性

杜先云 任秋道

(1.四川省成都信息工程学院数学学院 610225;2.四川省绵阳师范学院数理学院 621000)

一、引入

目前《高等数学》与《数学分析》教材中，对任意项级数收敛的内容涉及少，而大量级数的敛散需要确定.我们通过数列收敛方法来判定级数收敛.从新的角度去认识收敛数列的渐进性：当n无限增大时，可以认为收敛数列{yn}相邻两项的差所构成的数列{yn-yn-1}(n>2)，无限接近一个公差为0的等差数列，从而给出了利用yn-yn-1趋于0来判断数列收敛的方法.这说明了收敛数列各项变化的微小性.本文给出了任意项级数收敛的一个判定定理，讨论了一些余弦级数的敛散性.

二、任意项级数收敛的判定

引理设{yn}为一个有界数列.∀ε>0，∃N∈Z+，当n>N时，不等式|yn-yn-1|<ε恒成立，则数列{yn}收敛.

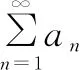
一个收敛级数任意加括号后所成级数仍然收敛，其逆命题不成立.但是有下面的定理：

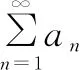
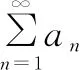
(a1+a2+…+an1)+(an1+1+an1+2+…+an2)+…+(ank+1+ank+2+…+ank+1)+…,

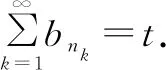
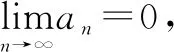
|Sn|=|bn1+bn2+…+bnk0+(ank0+1+ank0+2+…+an)|

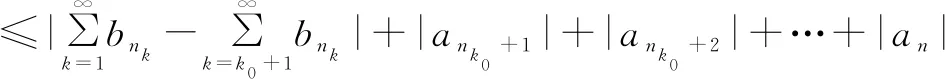
从而该级数有界.利用引理的推论可得结论.证毕.

这个定理推广了交错级数收敛的莱布尼兹定理，可以说给出了判定级数的一个简便方法.

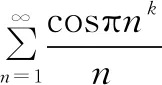
证明当k=1时，容易知道结论成立.设Z[0]={2i|i∈Z},Z[1]={2i+1|i∈Z}.当k=2s,s≥1时，根据二项式定理可得

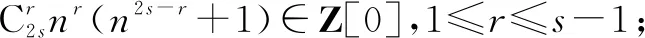
(n+1)2s-n2s-1∈Z[0]，[nk+(n+1)k]∈Z[1].

同理可得[nk-(n+1)k]∈Z[1].当k=2s+1,s≥1时，有同样的结论.因此，