提高高中数学教学质量的有效策略

石 滢

(江苏省盐城中学 224000)

当下高中数学教学中存在一个误区，就是在学生思维的培养上通常对知识传递产生依赖性，却不是采用专门的思维训练方式，使得学生解决问题的能力没有明显提升，学生的应试能力依然是衡量学生学习质量的重要标准.这就意味着学生数学综合素质停留在理论层面，没有落实到具体的教学工作中.所以，教师要着力提高课堂教学质量.

一、高中数学教学中塑造翻转课堂促进师生交互

翻转课堂与传统课堂的重要区别就是不按照教师讲课、学生听课的教学过程展开，而是学生自主学习，教师根据学生的知识需求展开教学.教师要注意引导学生，让学生对课堂教学内容有深刻的印象，并留存在大脑中，对学生更好地理解数学知识起到一定的促进作用.从翻转课堂教学形式来看，其是基于计算机技术展开的，教师将主要的教学内容制作为课件传递到指定的教学平台上，学生只要能上网，就可以登陆平台观看课件，达到课前预习的效果.在进行课堂教学的时候，教师在讲课之前用三五分钟的时间播放课件，让学生提出不懂之处，教师以帮助学生展开思维的方式实施指导性教学，而不是将教材内容托盘而出.当然，学生遇到难以理解的问题的时候，教师鼓励学生利用互联网查阅资料自行解决.互联网是教师与学生沟通的桥梁，可以确保教师对学生的学习情况全面了解，学生也可以与教师共同探讨问题，从而拉近了师生之间的距离，为提高教学质量创造条件.

比如：在直线与平面的位置关系教学中，如果设定一条直线a与一个平面之间没有公共点，就可以明确直线a与平面之间是处于平行状态的.可是，当直线a与平面之间只有一个公共点的时候，就可以明确直线a与平面之间是相交的;当直线a与平面之间有两个公共点的时候，就可以证明直线是在平面之内的.

让学生观看课件.课件所表达的内容是直线与平面之间的各种关系，用三维立体图象表达.直线是无限延伸的，平面也是如此.当平面与直线没有交点的时候，必然是处于平行状态的.教师操作课件让学生观看，也可以让学生操作课件，进行各种尝试，认识到，直面与平面平行，无论如何都不会有交点.

当学生对这个定理产生直观印象之后，教师就可以与学生讨论如何推导证明的问题.

已知：l∥α，l∥β，α∩β=m，求证：l∥m.

具体的证明过程如下：

取A∈α，由A、l确定平面γ，记γ∩α=a.由l∥α知l∥a.同理取B∈β,由B、l确定平面δ，记δ∩β=b，则l∥b.因而a∥b，则a∥β.又α∩β=m，则a∥m.但l∥a,所以l∥m.

证明完成后，教师要引导学生反思，了解判定定理的实质性内容，三个判定条件都是不可缺的.在定理的证明过程中，主要是找出与已知直线平行的直线.

二、高中数学教学中采用矛盾分析法指导学生分析问题

在高中数学教学中，教师要认识到数学知识本身就是一个矛盾体，在教学中要充分利用数学知识的这一点，引导学生用正确的方法学习数学知识并思考问题.矛盾问题属于哲学范畴.学生在思考问题的时候利用哲学思维，繁琐的数学逻辑就会变得清晰了.数学与哲学有关系吗？说到这里也许很多人不理解.世界上一些著名的数学家同时也是哲学家，比如伽利略，迪卡尔等等，他们在分析数学问题的时候会运用哲学的思维方式.哲学是抽象的，其要解决的是最基本的问题，也就是说，运用哲学思维可以寻求问题的本源.比如，数学中公理是如何形成的，就要对数学发展历史进行追溯，这其中就涉及到哲学问题.莱布尼兹是计算机二进制的发明者，他提出，如果哲学语言像数学中的符号那样精确的时候，一切都将成为必然，不会存在模糊的中间状态，或者是对的，或者是错的.计算机的运行模式就是间接模拟人的思维.可见，数学家在思考问题的时候，也会运用哲学思维模式.基于此，在高中数学教学中，数学教师不妨将哲学思维合理运用，对学生进行指导教学，让学生运用哲学逻辑解决数学问题，不仅学习效率提高了，而且对学生数学思维品质的培养非常有效.高中数学教学中，需要直接面对的问题就是教和学的问题，这就是一对矛盾体.运用哲学中矛盾论的观点对这个问题进行分析、研究，认识到教学中存在矛盾是必然的，数学教学尤其如此.数学知识中，各个部分之间同样存在矛盾，在各个知识环节以及每个知识点中都能够体现出来.教学内容不同，就要采用相应的的教学方法，所获得的数学结论也是不同的.

在教学中用矛盾分析法，用矛盾转化的规律对数学问题予以解决.

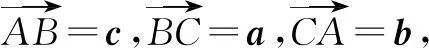
在这道题的证明中，需要观察条件，通过对条件进行推理就可以猜想出结果，之后将特殊值选择出来代入，进行验证，就可以明确结论.在证明的过程中，采用矛盾分析法将条件与结论之间存在差异找出来，同时将内在联系找出来，采用各种方法将双方的差异消除.由此可见，矛盾分析法属于是化归的思想，是按照思维规律进行操作的结果.