螺栓连接振动特性的仿真与试验研究

高飞，张澍，梁国利

（航空工业新乡航空工业（集团）有限公司,新乡 473000）

引言

螺栓连接方式在机械结构中应用十分广泛，被连接的结构件在预紧力和工况载荷作用下可产生复杂的力学效应，如微小滑移、宏观滑移、粘合等现象，在外载严酷时甚至会发生大幅度分离现象。含有非线性连接结构的模态无法采用有限元方法进行计算，必须将非线性连接结构理想简化为线性结构。通常采用的简化方式有：一是忽略摩擦对接触面的影响，将通过螺栓相互连接起来的零件直接固定在一起，固有频率的仿真结果大于试验数据结果，人为增加了结构的刚度，会给结构设计带来风险；二是局部约束法，只对零件的螺栓孔附近区域进行约束，忽略了结构接触面积改变带来的刚度变化影响，一定程度上降低了结构固有频率；三是采用杆单元等模拟螺栓连接，该法忽略了接触刚度对结构的影响[1-3]。

航空产品的振动工况考核是必要的一个环节，为了缩短研发周期，防止返工情况发生，产品在方案阶段往往需要借助仿真手段对结构振动强度进行评估，由于模态分析是振动分析的基础，模态的精度对振动分析的结果至关重要，因此对于装配体，对仿真分析中螺栓连接处理方式的研究很有必要。本文对不同形式螺栓连接的工装进行了模态试验研究和仿真分析，通过对仿真结果对比、修正分析，为机械结构中采用螺栓连接的简化提供了相应的参考方法，具有实际应用价值。

1 螺栓连接刚度理论

通常螺栓连接受力如图1所示,其中F0为螺栓初始预紧力，Fb为螺栓的拉力，Fm为连接件间的压力，Fe为所受外力载荷。这种连接结构可简化图1中(c)所示的模型，这里Kb、Km分别为螺栓和被连接件的轴向刚度[4]。

根据以上刚度模型，螺栓和被连接件受力分别为：

外载荷为：

则等效轴向刚度为：

1.1 螺栓的刚度计算

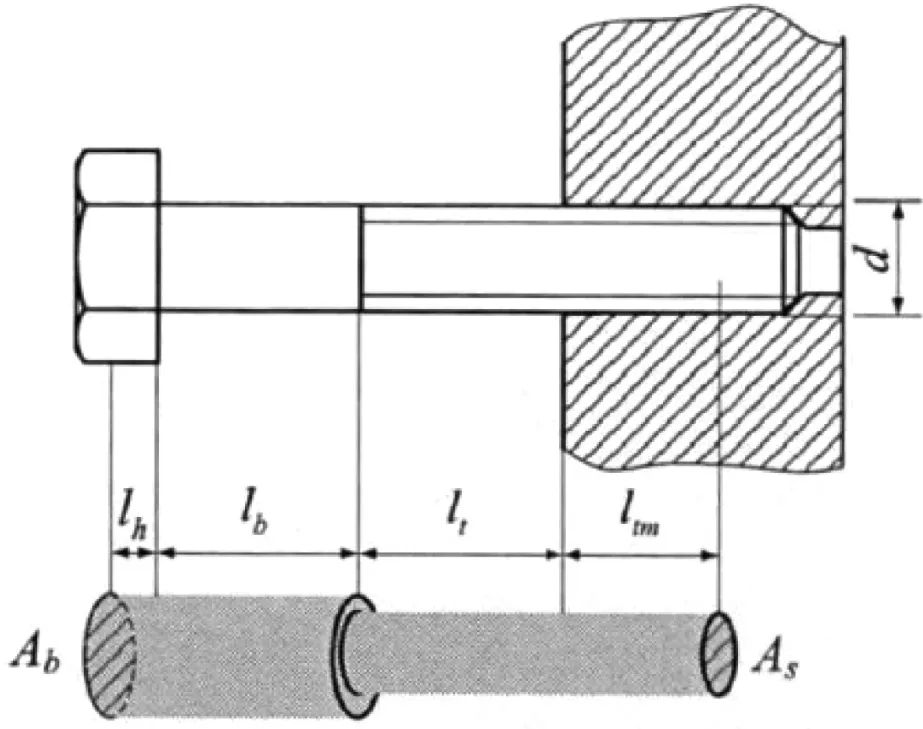
图2 螺栓尺寸示意图

根据德国的螺栓校核规范VDI2230，计算螺栓刚度时可简化为阶梯轴结构。如图2所示，Ab为螺栓的光杆横截面积，As为有螺纹部位的等效横截面积，lh、lb、ll、ltm分别为螺栓头、光杆、螺杆、收尾螺纹部分的等效长度，d为螺栓的公称直径，P为螺距。则有

则螺栓刚度为：

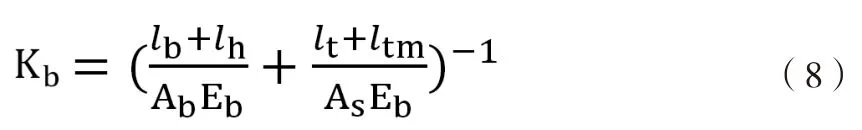
1.2 被连接件的刚度

被连接件在螺栓预紧力作用时假设只有螺栓孔附近的区域受压，则受压区域可认为是被连接件的等效实体（如图3所示），因此被连接件的连接刚度可等效为在受压区域的刚度。该区域的应力分布较为复杂，很难求出解析解，一般将被连接件受压区域简化为圆柱体、球体或圆锥体等三种形式，其中圆锥模型相对具有较好的精度，应用也最为广泛。

当两被连接件的材料和厚度相同时，连接刚度件的总刚度为：

采用螺栓连接的总刚度应为螺栓刚度和被连接件的刚度之和，公式中没有考虑结合面平面度、粗糙度等因素，刚度值具有一定的误差，另外计算过程繁琐，工程应用中效率较低，难以满足工程节点需求，因此研究一种在仿真过程中应用的螺栓连接刚度简化方法十分有必要。

2 模态仿真计算中螺栓连接刚度等效的分析

振动工装对产品的振动试验产品起到固定和支撑的作用，工装的振动特性对试验的结果有一定的影响，本节通过对螺接工装的模态特性分析，研究不同刚度等效方法对振动特性的影响。有限元分析过程中螺栓常用的处理方法有实体螺栓、梁单元、弹簧单元等，本分析采用实体螺栓和梁单元简化方法进行分析。

2.1 有限元模型的建立

所研究工装根据实际工装测绘，采用三维制图工具建模，工装由两个零件组成，通过7个M8螺栓连接，如图4所示。

模型各零件材料属性如表1所示。

模型单元采用SOLID186/187单元，单元数量为93 842，节点数量为216 943，单元的平均质量为0.8，符合网格质量要求。

2.2 螺栓连接刚度不同简化方式

为了得到快捷、准确的连接刚度等效方式，本节内容采用不同的连接方式对模型进行分析。

1）实体螺栓绑定约束

该种方式采用实体螺栓模型，螺栓与相连接的两个零件间进行绑定约束，如图5所示。

2）实体螺栓预应力

该种方法采用实体螺栓模型，同时施加螺栓预紧力，立板与底板接触面设置为摩擦接触，采用预应力模态进行分析，如图6所示。

3）采用压力角方式

该种方法中忽略螺栓，对螺栓压紧区域近似为一个锥形区域，根据尺寸计算压力锥半角约为15 °，将相连两个面分割出相应面积，施加绑定约束，如图7所示。

图3 被连接件锥形受压区域假设

图4 螺栓连接工装模型

4）采用梁单元简化

该方法将螺栓简化为梁单元，同时将相邻的两个面施加不分离约束，如图8所示。

5）弹簧单元简化方式

通过螺栓连接的两个体实质上为结合面上三个方向的刚度产生的作用，这里将每个螺栓连接处沿X、Y、Z三个方向分别定义三个弹簧，以模拟结合面上产生的连接刚度，如图9所示。

采用弹簧单元简化方法时，将每个弹簧刚度定义为输入变量，以模型的前两阶固有频率值为输出变量。首先对输入变量做参数优化分析，选取一个最优设计点，均衡前两阶固有频率，帕累托前沿图如图10所示。

2.3 计算结果及分析

通过对上述方法进行求解，模态结果如表2所示。

图5 工装螺栓连接约束

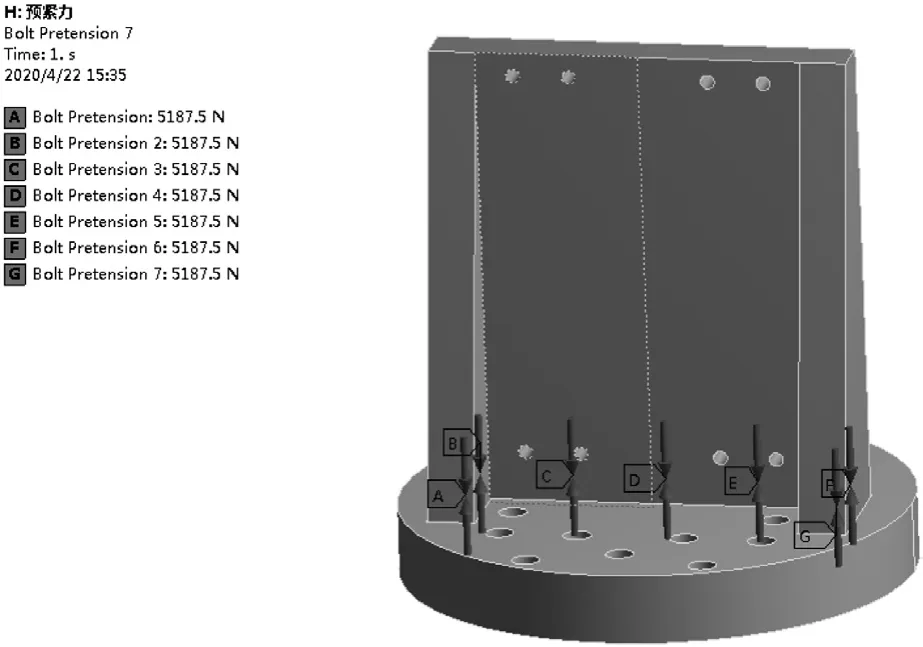
图6 螺栓施加预紧力模型

可以看出，不同简化方式所计算得到的固有频率基本一致，存在一定的偏差，但振型相同，如图11所示。

图7 压力角方式等效模型

图8 梁单元等效仿真模型

图9 弹簧等效刚度示意图

图10 帕累托前沿

从振型可以看出，第一阶振型为立板的扭转，第二阶振型为立板的摆动，第三阶振型为立板和底板的弯曲。

通过预应力模态分析可以监测到当工装预紧后整个模型的接触状态，施加预紧力后，可以看到立板和底板的接触状态为黏着状态，即绑定在一起，见图12。计算模态时将该状态带入动力学矩阵方程，进而进行模态分析。

3 螺栓连接工装的模态试验研究

上一章采用有限元建模方法对含有螺栓结合部的工装结构进行了有限元模态分析，得到了不同简化连接刚度方法的固有频率和模态振型。为了对这些建模方法的精度和有效性进行评估，需对结构进行模态测试，确定较优的螺栓连接刚度等效方法。

3.1 模态测试模型搭建

针对上面分析的工装，采用东华测试公司的DHDAS动态信号采集分析软件进行模态测试。

该结构可视为悬臂结构，主要振型为立板的摆动或扭转，因此在模态测试建模时可以只建立立板部分，立板的平面尺寸为180×200 mm，由于底部力锤无法敲击，因此建模时200 mm高度取上面180 mm。建立XY方向的平面模型，平面是X方向180 mm，Y方向为180 mm，将Z向作为激励和响应振动方向。一般要求测点数目多于所要求的阶数，这样得出的高阶模态结果才可信。测点过多会使测试工作量增加很多，过少可能会漏掉某阶模态，这里将模型的每个边三等分，得到16个节点，选择所有的节点，点击自动生成测点，此时会自动生成16个测点，如图13所示。

模态实验方法中的单点拾振法，使用一把力锤和一个加速度传感器来完成模态实验，选取拾振点时要尽量避免使拾振点在模态振型的节点上。本次测试模态为自由模态，因此需要将工装采用具有弹性的橡皮绳吊起来进行测试，如图14所示。

系统连接如图15所示，把力锤（已安装力传感器）输出线接到数据采集仪1-1通道，加速度传感器安放在工装的第13测点，输出信号接到1-2通道。

表2 不同等效模型固有频率结果

图11 前三阶模态振型

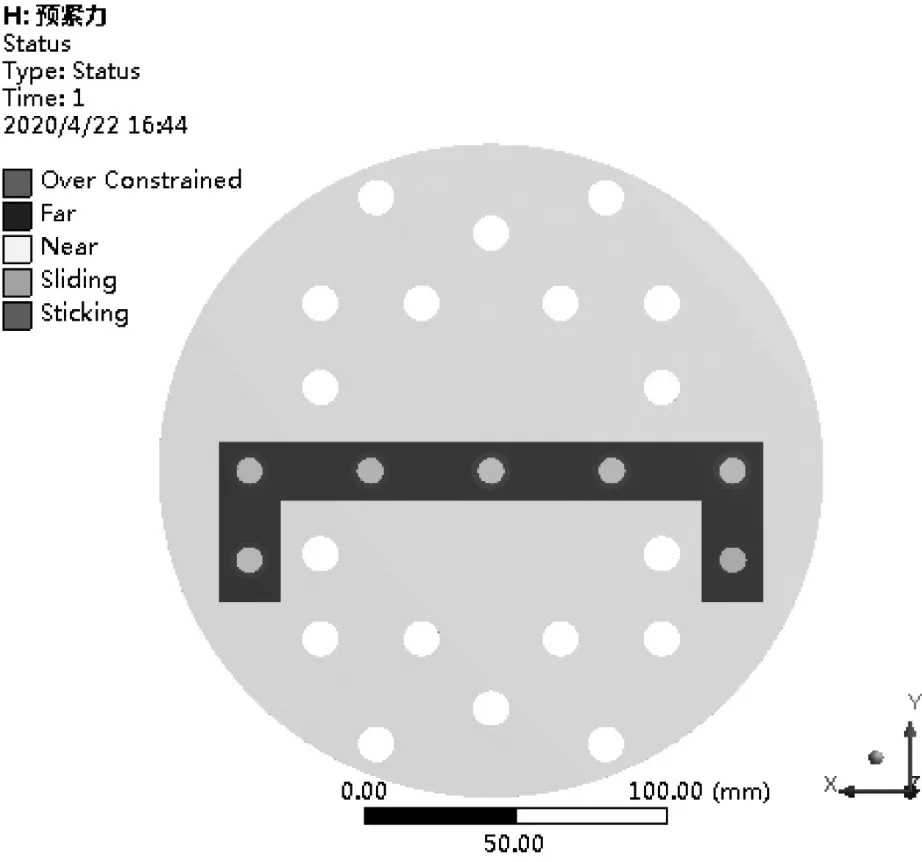
图12 预紧力模型中连接件接触状态

图13 工装结构示意图和测点分布示意图

3.2 模态参数提取

采用模态测试仪中的模态参数识别软件，对测得模态参数进行识别，将噪声点过滤掉，识别频响曲线中峰值，出现红点标记，由于产品工作频率均在2 000 Hz以下，因此模态试验时主要提取2 000 Hz以内固有频率，如图16所示。

通过频响曲线可以看出，前2 000 Hz内有两阶固有频率，分别为1 214 Hz和1 270 Hz，振型如图17所示。

图14 测试工装固定图

图15 测试系统连接图

图16 频响曲线图

图17 前2阶模态振型

3.3 模态结果验证

采用模态置信准则对实验结果的可靠性进行验证，模态置信准则是检查两阶模态一致性和独立性的重要指标，实验模态置信准则柱状图如图18所示。

图18 模态置信度

模态置信度采用MAC值评判，MAC值接近1，表示两者线性相关，相关度越高的两个模态向量对应的模态振型越相似；MAC值接近0，则表示线性无关，即模态振型不相似。图8中非对角线上表示不同阶次的模态振型之间MAC值低于0.05，表明前2阶振型向量相互之间满足正交性，不存在振型混淆现象，说明了实验结果的可靠性。

3.4 试验与仿真结果对比

利用模态测试结果对有限元分析的四种螺栓连接刚度等效方法进行验证，包括固有频率及振型，根据试验结果，选取前两阶模态进行对比，固有频率对比如表3所示。振型对比如图19、20所示。

采用有限元方法获得结构的前2阶固有频率与试验固有频率误差均在5.1 %以内，其中，采用压力角方式和预应力方式等效螺栓连接刚度误差较小，均在3 %以内，采用梁单元简化方式误差最大，第二阶固有频率误差为5.1 %。因此，采用压力角方式和预应力方式可以准确等效螺栓连接刚度，具有较好的精度，且可以简化计算模型，提升计算效率，对于大装配体效果较为明显。

4 结论

对螺栓连接的产品进行有限元分析时，可采用连接刚度等效方法对模型进行简化处理，不仅简化了仿真模型，而且还能保证结果的精度。通过将实体螺栓模型、预应力模态、压力角方式、梁单元等四种连接刚度等效方法的仿真结果和模态试验结果对比分析发现，预应力模态和压力角简化方式的精度最好，可以作为仿真分析中螺栓等效连接刚度的可靠方法，对实际工程的有限元仿真具有参考和应用价值。

图19 模态仿真与测试第一阶振型对比

图20 模态仿真与测试第二阶振型对比