基于惯性权重和学习因子动态调整的粒子群算法

2021-01-13吴永红曾志高

湖南工业大学学报 2021年1期

关键词：惯性全局种群

吴永红，曾志高，邓彬

（湖南工业大学计算机学院，湖南株洲 412007）

0 引言

粒子群算法是一种经典的元启发式算法[1]，该算法由C.Reynolds 于1987 年对鸟类觅食行为进行模拟研究时得出，他提出如下模拟鸟群个体简单行为的3个规则：

1）防止鸟群发生碰撞，即减少与其他粒子产生碰撞；

2）鸟群个体保持速度相近，即速度与邻近粒子尽可能相近；

3）鸟群个体朝中心靠拢，即朝粒子群中心尽可能聚拢。

其后，J.Kennedy 等基于C.Reynolds 的研究结论，在1995 年经过进一步研究提出了一种粒子群优化（particle swarm optimization，PSO）算法。该算法对之前的算法进行了参数简化，算法原理更为简单，易于实现[2]，因此得到许多研究人员的关注，并且被应用于处理各种优化问题。例如：张鑫等[3]提出了一种自适应简化粒子群优化算法，按照一定规律引入分布的锁定因子，从而粒子位置的惯性权重可以通过锁定因子自适应配置，导致算法收敛速度得到了有效提高，但是仍然存在鲁棒性较弱、收敛精度较低等缺陷；王永贵等[4]为了增加种群的多样性，在算法中引入了动态分裂算子，以此避免陷入局部最优解，然后通过采用指数衰减的惯性权重，平衡粒子的局部以及全局的搜索；杜美君等[5]提出了一种基于相似度动态调整惯性权重的方法，它将更小的惯性权重值赋予靠近目前最优粒子的个体，但是算法收敛速度较慢，当处理复杂函数问题时，耗时较长。PSO 算法也存在很多的局限，在迭代时粒子群体多样性不断降低，导致算法容易陷入局部最优解、收敛速度后期变慢或者出现早熟收敛等问题。上述研究者的改进算法对增强种群多样性有很大帮助，同时有助于平衡算法局部搜索能力与全局搜索能力，在一定程度上提高了PSO 算法的寻优精度，也加快了算法的收敛速度。

以上各算法主要针对粒子群算法在迭代过程中种群多样性降低、收敛速度较慢和寻优精度较低等问题[6-10]而提出改进方案，但是没有对算法的惯性权重和学习因子进行动态调整，有可能导致算法出现早熟收敛现象。针对这一问题，本文提出一种自适应的调整惯性权重和学习因子的粒子群算法，利用惯性权重和学习因子的动态改进调整，以期提高算法的性能。对比实验结果显示，改进算法具有较强的寻优能力和收敛性。

1 基本粒子群算法

在粒子群优化算法中，所有粒子组成一个种群，每个个体可以被看作一个具有位置和速度的粒子，待求解问题的候选解用粒子位置表示。种群开始初始化，且各粒子被随机给予一个位置和速度，不同个体分别代表不同的随机解，在不断迭代后最终得到粒子最优解。随着粒子位置与速度的不断更新，局部最优解和全局最优解随之更新。在迭代期间，各个粒子用跟踪个体极值与全局极值的方式完成更新。pbest(i, t)表示到第i 个粒子第t 次迭代期间所发现的粒子最优位置，pbest则表示群体迄今为止所发现的最优位置，分别用式（1）与式（2）来表示粒子更新后的速度和位置。

基本粒子群算法的速度和位置更新公式如下：

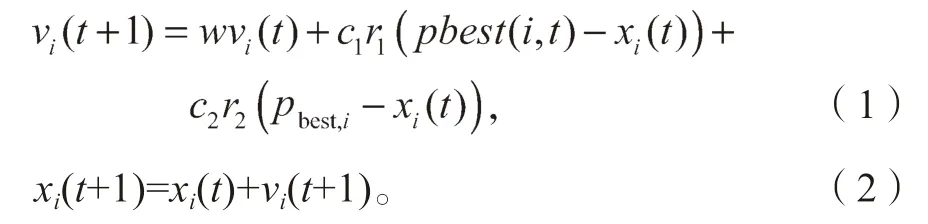
式中：w 表示惯性权重；

vi(t+1)代表第i 个粒子当前迭代速度；

xi(t)为第i 个粒子的位置；

r1、r2为介于[0, 1]区间内的随机数；

c1、c2为非负的学习因子。

惯性权重是重要的进化参数，它决定的是粒子先前飞行速度对当前飞行速度的影响程度。当惯性权重较小时，整体的局部搜索能力较强，全局搜索能力较弱；惯性权重较大时，整体的局部搜索能力较弱，全局搜索能力较强。因而，为优化算法寻优能力与算法性能，并平衡粒子的局部搜索与全局搜索能力，采用调整惯性权重值的方式来完成。算法在搜索速度与搜索精度上能否适当平衡，取决于能否找到适当的惯性权重值，这也成为业内学者们的一个重要研究方向。

基本粒子群算法仍然有很多缺陷，如算法经常产生早熟收敛现象，环境的变化会影响算法性能，经常会受到全局极值和个体极值的影响而陷入局部最优等。针对以上问题，本文对算法的惯性权重和学习因子进行了动态改进调整，以提升算法的寻优能力和收敛性。

2 改进的粒子群算法

粒子群算法的速度迭代公式中有如下3 个重要参数：惯性权重w 和学习因子c1、c2。惯性权重w 影响着粒子先前的飞行速度对于当前的飞行速度的影响程度，惯性权重的选取对于平衡算法的全局搜索能力和局部搜索能力有着重要意义。在迭代过程中，要考虑算法的全局性和局部性，要采取合适的惯性权重来进行搜索。本文利用改进后的幂指函数算子，将其加入到惯性权重中，以总的迭代次数为基础，在搜索时让每个粒子扩大搜索空间，以此增大种群多样性。因此，本文采用改进惯性权重值的策略。对比实验结果表明，动态调整后的惯性权重能提高算法搜索性能，有效改善收敛状况，随着算法不断迭代，惯性权重值动态改变，表达式为

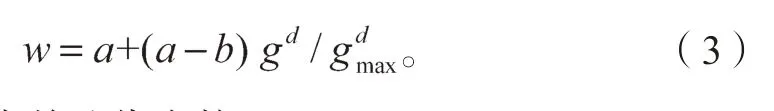
式中：g 为当前迭代次数；

a、b、d 为参数；

gmax为迭代次数的最大值。

作为算法运行中的重要式子，c1是粒子具有自我学习总结能力的体现，代表的是个体自我认知；学习因子c2是粒子具有向表现更好的粒子学习的本领体现，代表的是粒子的社会认知。需要设置恰当的c1、c2以便于粒子进行搜寻。初期要关注个体自我认识的能力，后期则应注重个体获取社会信息的能力。本文设置如下学习因子：

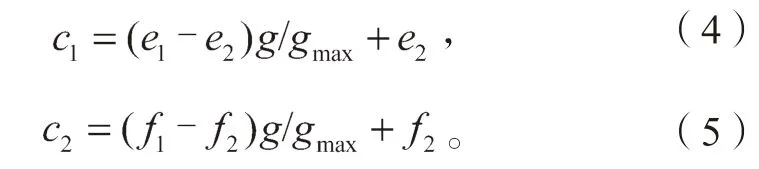
式（4）（5）中e1、e2、f1、f2为参数。

改进后新的粒子速度和位置迭代公式跟原始算法相同。

与基本粒子群算法相比较，对基于惯性权重和学习因子动态调整的粒子群算法的速度公式作出调整时，实现了算法随着迭代次数变化而动态变化，其全局搜索能力有效提高，粒子的收敛性也得到了加强。然而，当遇到一些复杂的多峰值函数曲线的寻优问题时，基于惯性权重和学习因子动态调整的粒子群算法，依然存在许多问题，收敛速度以及精度仍达不到要求等。如当受到局部阴影的作用时，光伏阵列的输出曲线将会变得错综变幻，由于多峰值的产生，大大增加了整体寻优的难度，也可能使基本粒子群算法和改进粒子群算法显示早熟迹象，而导致产生局部极值。

2.1 改进的粒子群算法流程

基于惯性权重和学习因子动态调整的粒子群算法的步骤具体描述如下：

Step 1 对粒子群初始化，产生各个粒子的位置和速度，并进行子种群划分，最大迭代次数gmax，种群规模Spop等。

Step 2 设置模型，初始化后存放粒子的速度、位置和适应度值，然后在种群中挑选出具有最佳适应度值以及对应最佳位置的粒子。

Step 3 更新惯性权重w 与学习因子c1、c2。

Step 4 对各个粒子分别评价，并更新粒子的位置、速度。

Step 5 随着粒子位置不断更新，分别计算粒子的适应度值，找出每个粒子所能得到的个体最优值pbest，当每找到一个新的pbest 时，再与之前的最优值进行比较，将更优值更新为全局最优值pbest，经过粒子的不断更新迭代，最终更新得到全局最优解pbest。

Step 6 判断算法能否达到终止标准，若达到，则输出最优值；若没达到，则返回步骤3。

2.2 流程图

根据上述改进粒子群算法的流程，绘制如图1 所示流程图。

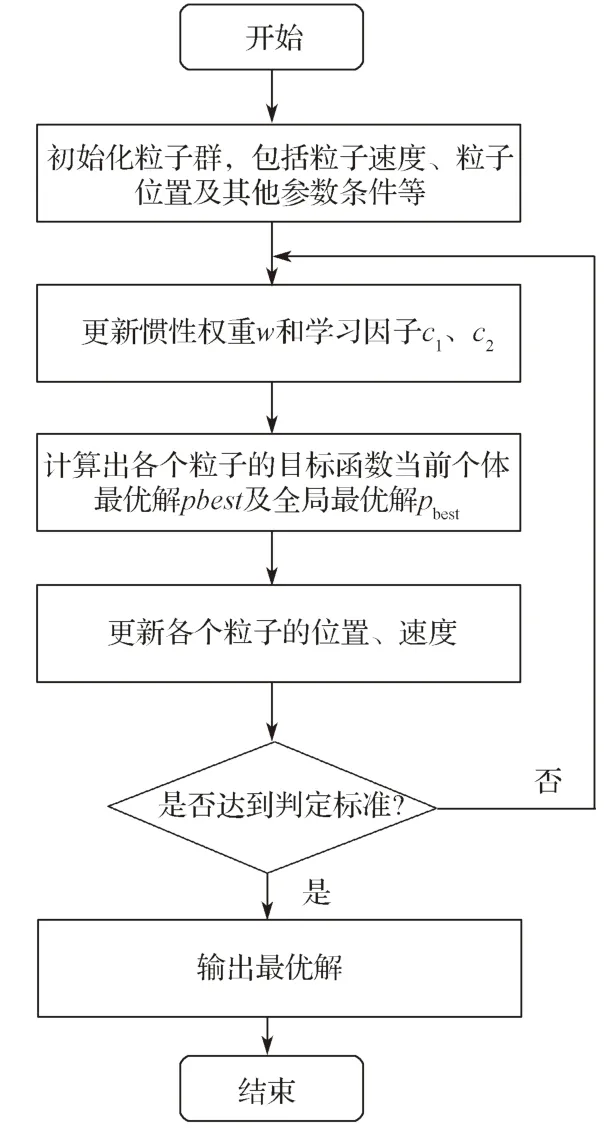
图1 改进粒子群算法的流程图Fig.1 Flow chart of the improved particle swarm optimization

3 实验和分析

为了验证本研究中所提出的改进的粒子群算法是否有效可行，实验组使用了6 个典型测试函数来进行测试，并且与基本粒子群算法进行比较。仿真实验的运行环境为Matlab2016a， 64 位 Windows10的操作系统，硬件参数为 Intel(R) Core(TM) i5-4300U CPU @ 1.09GHz 处理器、内存是为 GB。定义6 个测试函数如下：

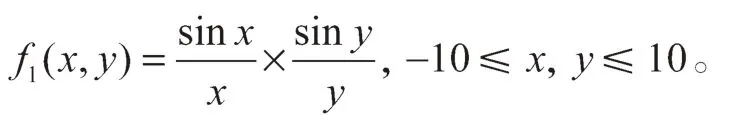
函数在（0, 0）处存在唯一极大值，且在周围分布着许多局部极值。

函数在（0, 0）处取得极大值0。

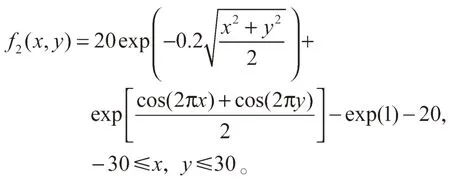
函数在（0, 0）处取得极小值0。

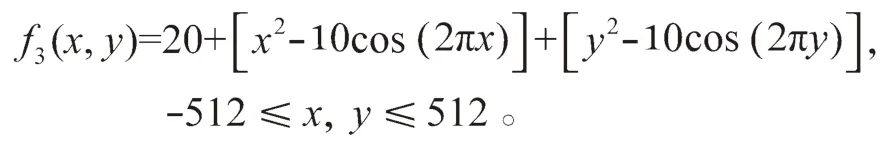
函数在（0, 0）处存在最小值 0。

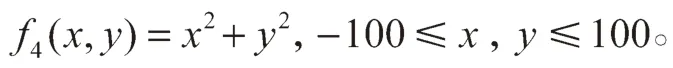
函数在（1, 3）处取得极小值0。

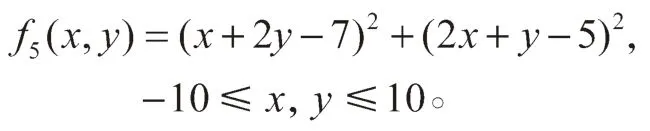
函数在（0, 0）处有极小值0。

设置基本粒子群算法的运行参数如下：c1取值为1.5，c2取值为1.7，种群规模Spop取值为20，种群维数为10，实验共运行20 次，每次运行迭代500 次，求其平均值。设置的改进粒子群算法的参数基本粒子群算法的相同。

4 实验结果及分析

4.1 测试结果

为了对改进的粒子群算法的寻优效果进行测试，对基本粒子群算法和改进粒子群算法各运行20 次，得到各自的平均值，所得测试结果如表1 所示，表中IPSO 代表改进的粒子群算法。其中，最优值是得到的所有解值集合中最好的值，最差值是得到的所有解值集合中最差的值，最优点为20 次最优值位置的平均值。由表1 可知，除了函数f5以外，IPSO 均找到了最优值；所有测试值中，改进粒子群算法的标准差更小，优化结果比基本算法更优。

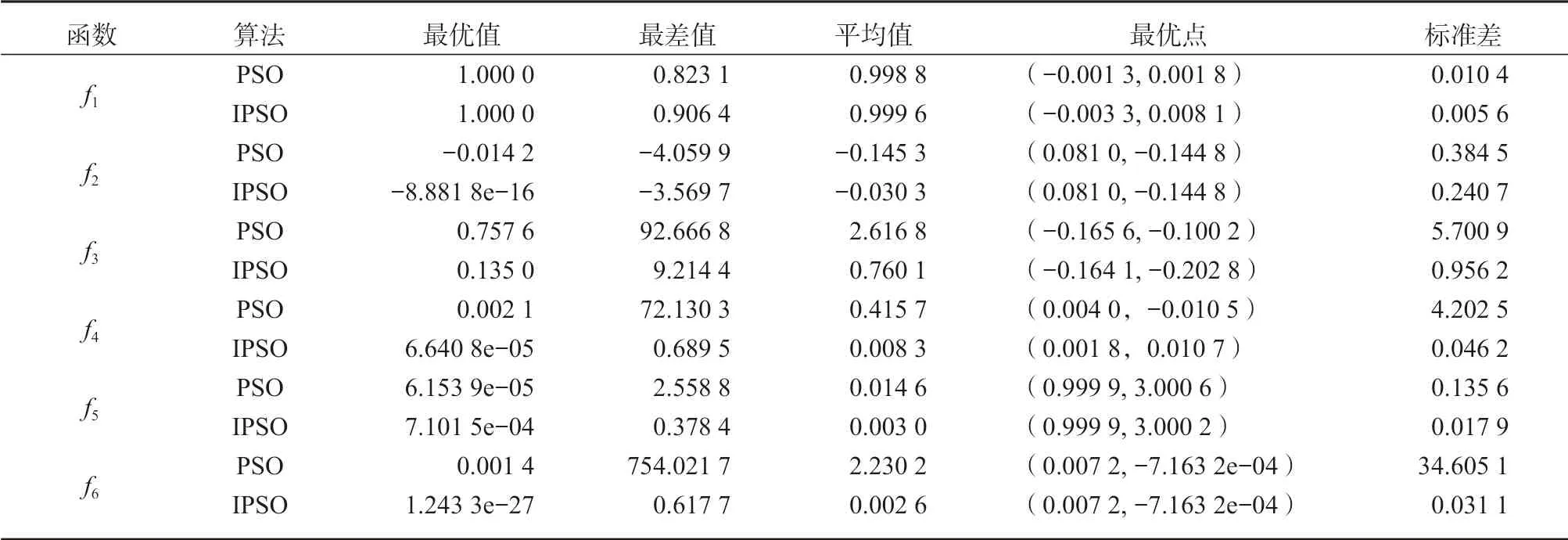
表1 两种算法的结果比较Table 1 Comparison of the results of the two algorithms

4.2 函数的收敛曲线

基本算法和改进算法的收敛曲线如图2 所示。

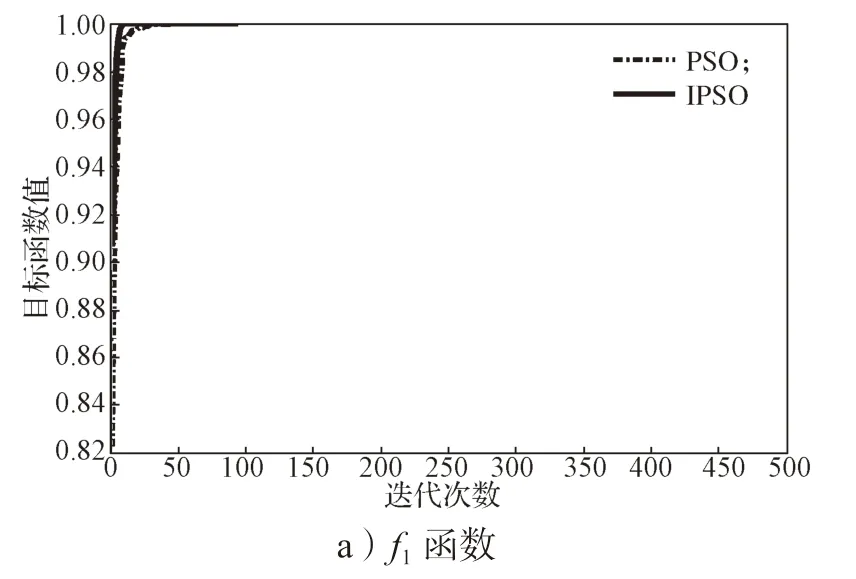
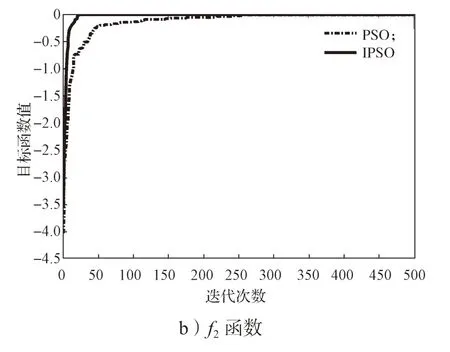
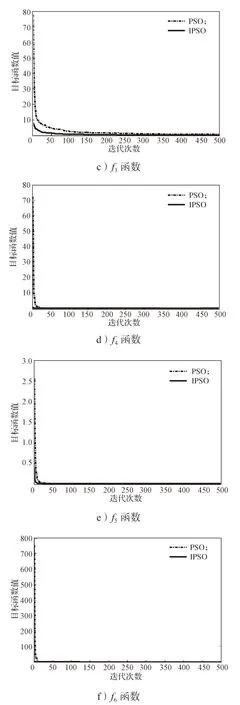
图2 基本粒子群算法与改进粒子群算法在不同函数下的收敛曲线Fig.2 Comparison of convergence curves between the standard and improved particle swarm optimization algorithms under different functions

由图2 中各个函数的收敛曲线可以得知，随着迭代次数的增加，粒子群逐渐向最优值聚集，改进算法得到的收敛曲线比基本算法得到的收敛曲线更快接近水平方向，说明改进的算法收敛速度增强，改进的PSO 算法的收敛性更好。