迁移与联结：小学数学规定性知识的教学探析

李一婷

【摘 要】在小学数学教学中，规定性知识的教学存在着机械刻板、不够深入的现象。本文以苏教版数学一年级下册“认识元角分”为例，通过分析教科书相关内容编排情况及学生学习情况，提出迁移关联知识、突破认知瓶颈的具体对策：巧借“计数器”，理解新关系;利用整数竖式，创造新算法;联系学生实际，调整学习内容。在规定性数学知识的教学中，教师不仅要善于转变观念，变“教”为“学”，更要做到瞻“前”顾“后”，促使有效迁移和联结。

【关键词】规定性知识 联结 迁移

一、一次听课引起的思考

笔者在一次教研活动中听取了一节公开课——苏教版数学一年级下册“认识元、角、分”。在教学元、角、分的关系时，一个教学小片段引发了笔者的深思。其教学实录如下：

师：同学们，一本练习本1元，我付10角可以吗？

生：可以，10角就是1元。

师：对了，我们一起来数一数：1角、2角、3角、4角……9角、10角。10角就是1元，1元等于10角。那你们知道1角等于几分吗？

生：我知道，1角等于10分。

师：你是怎么知道的呢？

生：我妈妈告诉我的，1角就是10分。

师：真棒！那我们再来数一数：1分、2分、3分、4分……9分、10分。1角等于10分。这就是元、角、分之间的关系。

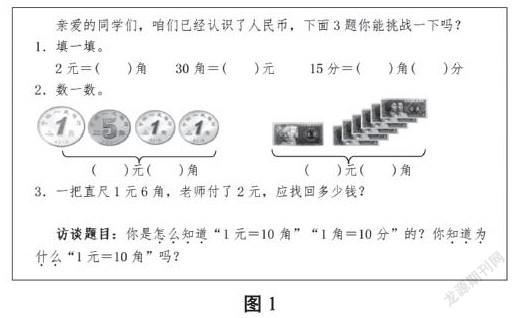
翻阅义务教育教科书，笔者发现教材编排与上述教学过程相同：①通过购物情境告知学生“10角就是1元”;②通过数数感受“1元=10角”“1角=10分”。一切看上去畅通无阻、水到渠成，但似乎又有些说不清楚、道不明白的遗憾。从知识类型角度来说，元、角、分之间的关系是数学中的一种规定性知识，对于规定性知识的教学，教师往往无从下手，似乎只要简单告知学生就能完成教学，那学生对这些知识到底掌握得如何呢？课后，笔者对这个班的学生做了一个测试和访谈（见图1）。

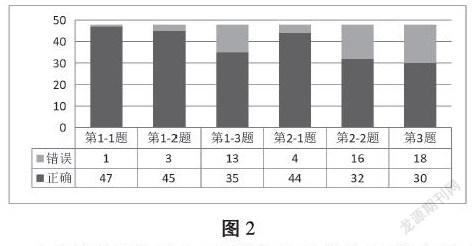
测试完成后情况统计如图2。第1-1题、第1-2题和第2-1题学生完成情况较好，正确率均达到了90%以上，而第1-3题、第2-2题及第3题完成情况一般，正确率分别为72.9%、66.7%和62.5%。正确率较低的这三题均涉及了元角分之间的间接转换，而不是像“2元=（ ）角”这样的直接转换。在访谈中，学生对于“怎么知道‘1元=10角’”这个问题的回答均为“老师教的”“家长说的”“看书的”三种情况中的一种，至于“为什么‘1元=10角’”则鲜有学生能回答。从测试和访谈的结果来看，通过上述教学，学生对于元、角、分关系的认识浮于表面，因此也只能完成较为简单的、低水平的习题，并未真正理解三者之间的关系，故而对于稍复杂的、中高水平的习题完成效果较差。

在小学数学教学中，像这样“人为规定”“约定俗成”的知识并不少见，在教学时也无不存在着机械刻板、不够深入的现象，学生往往掌握效果极其一般。如何让学生理解规定背后的原因，体会规定的合理性和必然性，让“规定性的知识”的学习变得有意义、有意思呢？这都是值得我们深入思考和躬身实践，寻求解决办法的问题。

二、迁移关联知识，突破“元、角、分”认知瓶颈

德国数学家康托说过：“数学的本质在于它的自由。”任何数学规定性知识在其“被规定”“被浓缩”之前，并不是无中生有的，也不是枯燥乏味的，而是有着其背后深刻的“故事”和“原理”。那么，元、角、分关系背后的“原理”又是什么呢？如何让学生深刻理解它们三者之间的关系呢？笔者做了以下一些思考和尝试。

（一）巧借“计数器”，理解新关系

“认识元、角、分”是一年级下册第五单元的内容，此前，学生已经通过计数器认识了“个位”“十位”和“百位”，感知了“10个一是1个十”和“10个十是一百”。整数的三个数位与人民币的三种单位似乎可以对应，而“满十进一”的规则也同样适用于元、角、分之间的换算。因此，笔者灵机一动，能不能借助计数器来认识新的关系呢？

师：同学们，为了便于计算，我们规定了元、角、分之间的关系与百位、十位和个位之间的关系类似。我们可以在计数器上来拨一拨、数一数。

（出示贴好“元”“角”“分”的计数器）

师：老师拨，大家一起来数。1角、2角……

生：1角、2角、3角……9角、10角（1元）。

师：对，10个1角就是1元，所以我们说，1元=10角。

师：那你们知道1角等于多少分吗？

生：可以在计数器上拨一拨、数一数。

师：那你来拨一拨，我们一起数一数。

生：1分、2分、3分……9分、10分（1角）。

师：那你知道了什么？

生：10个1分是1角，所以1角=10分。

师：看来，计数器的作用真大，不仅可以帮助我们数数，还可以帮助我们数“钱”。（学生开心地笑了起来）那从这个“计钱器”上，你还能知道些什么知识呢？

生：我想到了“元”和“分”之间的关系。因为“10个十是一百”，那“10个1角是1元”“10个1角就是100个1分”，所以“1元等于100个1分”。

師：哇，你真是个会思考、会推理的孩子。掌声送给你！

在这个过程中，改编原有的学具——“计数器”，制作新学具——“计钱器”，让学生在熟悉的数数的情境中迁移已有的知识，从而内化新知识，达到了轻松而高效的学习效果。荷兰数学教育家弗赖登塔尔认为：数学教育方法的核心是学生的“再创造”。作为教师，我们不必将各种固定性的知识灌输给学生，这样的学习对学生来说是不加判断的机械记忆，是一种零散的浅层学习。教师应该创造合适的条件，引发学生的深度学习，让学生充分联系自己的已有知识经验，主动地理解、联系、迁移和建构知识，这样，统一的规则、法则和定律在课堂中自然就会呼之欲出，学生自然也掌握得更牢固，记忆也更深刻。

（二）利用整数竖式，创造新算法

通过初步尝试，笔者感受到了利用计数器来认识人民币的相关知识对学生大有益处。那么整数计算的方法是否同样可以适用于人民币的计算呢？笔者开始了第二次尝试。

通常情况下，学生在计算诸如“5角和8角合起来一共是多少钱”的问题时，普遍采用三种方法——①学具操作：先摆出5张1角，再摆出8张1角，数一数一共有多少个1角，再说一说是几元几角。②先计算后换算：5角+8角=13角，10角=1元，1元+3角=1元3角。③分与合推想：把8角分成5角和3角，先算5角+5角=10角，10角=1元，再算1元+3角=1元3角。这三种方法思路虽然都比较清晰，但都有各自的弊端：方法①需要借助学具摆一摆，再想一想、算一算，这种侧重依赖于具体形象的方法往往过于烦琐，不够简便;方法②与方法③则需要学生经过三步思考才能逐步推导出答案，完全脱离了具体的实物，这种方法对于一年级的学生来说过于抽象，学生难以在头脑中直接有条理地进行思考和计算。

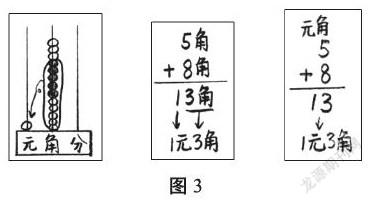
在教学中，笔者鼓励学生继续借助计数器，并尝试列竖式进行计算，学生积极思考，想出了多种方法（如图3）：

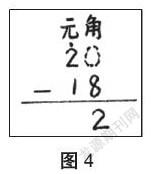
而后，又利用“元、角、分竖式”计算了“2元-1元8角”（如图4），学生纷纷表示：用竖式来计算人民币的加减法太方便了！

小学生思维发展经历着从具体形象思维为主向抽象逻辑思维过渡的阶段，纯粹的具体形象（摆学具）或纯粹的抽象（推理）都不利于学生的数学学习。因此，我们要迁移整数竖式计算的方法，架起具体与抽象之间的桥梁，帮助学生掌握数学知识，发展思维能力。纵观小学阶段的数学学习，像这样利用计数器或竖式进行计算的方法同样适用于“每相邻两个单位之间的进率是10”的长度单位“米”“分米”“厘米”“毫米”之间的换算和计算。

（三）联系学生实际，调整学习内容

苏教版数学一年级下册第五单元“元、角、分”的学习内容一共安排了3个课时，分别是“认识1元及1元以下的人民币”“认识大于1元的人民币”，以及“练习十”。但在实际教学中，3个课时是远远不够的，并且学习的内容跨度较大，因此应根据学生的实际情况，适当地进行调整。

可以调整章节学习内容的顺序。如，在教学第五单元“元、角、分”时，练习中经常会出现超过20的退位减法及两位数加两位数的进位加法，而这部分学习内容被安排在第六单元，显得有些滞后。因此，在教学中，教师可以根据自己的教学情况，合理调整单元教学内容的顺序，这样更有助于学生学习计算人民币。

可以适当增加变式练习内容。在苏教版教学教材中，“元、角、分”这一单元的练习十第一题直接出示了元、角、分的换算，但在前面的两节新授课中并未对人民币的换算和计算加以强化，由此导致大部分学生不会换算和计算。人教版的一年级教材编排了“简单的计算”这一课时，将人民币的单位换算和加减法计算作为例题进行教学，进而拓展到解决实际问题，这样有梯度的习题安排有助于学生深入掌握。因此，在教学时，我们可以适当增加课时和练习内容。

三、迁移与联结：数学深度学习的关键

在小学数学的学习内容中，有大量的规定性知识，主要是一些数学概念、名称、术语、表示方法等，这一类知识往往比较抽象，学生不易理解和掌握。在教学中，我们要努力做到以下几点：

（一）转变观念，变“教”为“学”

史宁中教授说：“数学素养的培养，特别是创新人才的培养，是‘悟’出来的而不是‘教’出来的。”在教学中，我们要关注规定性知识的教学，转变教学的方式方法，根据学生已有的知识经验，设计或提供可探索的情境，让学生在探索的过程中迁移、运用所学知识，“悟”出解决问题的方法，从而更好地理解数学，实现深度学习。

（二）瞻“前”顾“后”，促使有效迁移和联结

作为一名小學数学教师，要熟悉学生的已有知识经验，更要十分熟悉学生将要学习的知识，要掌握整个小学阶段的数学内容及其体系，要了解规定性知识的“来龙去脉”，进一步展现“浓缩”背后的精华，这样才能全面而准确地对规定性知识展开教学。

一次小小的尝试，仅仅只是规定性知识教学探索的一个开端，规定性知识创新教学方法的研究任重而道远。了解规定性知识的主观特征和产生背景，理解规定背后存在的合理性，带领学生经历知识产生的过程，才能形成规定性知识有效学习的路径。