把握度量本质理解分数的意义

陈瑛

【摘要】本文以《分数的意义》教学为例，论述把握度量的本质以理解分数意义的策略，通过不同教材的对比分析，理解教材之“意”;通过学情调查，了解学生对多个物体的整体概念薄弱;通过凸显单位、单位累加、砌“墙”延伸等方式，探寻有效的教学策略。

【关键词】《分数的意义》 理解分数 度量

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2021）37-0086-03

“分数的意义”是小学数学教学的一个难点，由于学生认知的阶段性及对分数度量的经验存在局限，他们无法真正理解“分”与“数”，对分数意义的认识不够深入。而巧用度量能有效地帮助学生理解分数实际是一个“数”，可以通过数分数单位的数量得出这个“数”，它是分数单位的累加。为此，笔者尝试利用“单位”降低学生对分数的认知难度，帮助学生完整地构建分数意义的概念体系。

一、理解教材之“意”

数学教育家张奠宙教授指出，分数一般有四种定义：份数定义、商定义、比定义、公理化定义。笔者查阅了苏教版、人教版、北师大版和浙教版小学数学教材中的相关内容，得出四个版本教材均有“份数定义”;各版本教材中度量的角度含量各不相同，北师大版度量的角度呈现更丰富;浙教版从“商定义”入手;人教版研究分数的产生是从度量开始;北师大版的“剩下的不足一段绳子怎么记？”同样是测量，要解决的是“不够测量怎么办”的问题，同时给出了方法：先用纸条的一半去测量，发现不行的时候用纸条的[14]去测量。各版本教材的立足点虽不一样，但都紧扣分数的本质。因此，从“份数定义”到“商定义”，是数系的一次扩充，更是一次跨越与升华。

由此，“分数的意义”是小学数学教材对“认识分数”的第三次呈现，对分数意义的理解，不仅是内涵的深入及外延的扩展，而且是深层次的认识和理解，也是一个逐步完善、逐渐系统化认识分数的进程。

二、深挖学生之“困”

五年级的分数教学要深入知识本质，了解知识的脉络及前后联系、厘清难点。为此，笔者在课堂上对学生进行了教学前测。

1.出示问题1：用至少两种方法表示[14]，并说明理由。

班级里有93.5%的学生用2种或3种方法表示[14]，但并未出现3种以上的方法。这些方法中是以画图为主要方式，并且集中在把一个长方形或正方形、圆平均分成4份，涂色表示其中的一份;仅有4.3%的学生用线段图表示。（如图1～图5）

由此可见，学生对分数的认识停留在一个图形、一个物体的平均分，具有一定的局限性。而仅有13%的学生把一些物体组成的整体平均分表征出[14]，集中表现在下面三种情况。（如图6～图8）

由上述案例可知，学生在三年级时，已经从平均分一个具象整体（一个物体、一个图形或一个计量单位等）的几分之一和几分之几，逐步过渡到认识一个抽象整体（一些物体组成的一个整体）的几分之一和几分之几。但到了五年级再学分数时，由于时隔一年半，学生遗忘率高，不难看出，他们对“将一个具象整体平均分”的印象深刻，这也与学生的认识水平有关。

2.出示问题2：下图中的三角形表示[14]，请你在方框里用三角形表示出“1”，并阐述理由。（如图9）

这道题中学生的答案相似，几乎都将图9右边的方框理解为一个图形，其中[14]就是左邊的三角形，于是通过画图补齐这个图形，主要画法如图10～图12（见下页）。

此外，全班还有13%的学生不会做题，8.7%的学生并未按原来的大小来画，而是将整个长方形框平均分成了4份;但几乎没有人想到可以在图框中画4个独立的三角形。

由此可知，学生对多个物体组成的整体概念很淡薄，这是因为题目存在难度，还是学生形成了思维定式？为此，笔者不由得思考：五年级下册的分数再认识和三年级的两次分数学习区别在哪里，联结点又在哪里，在后续的学习中又将起到怎样的作用？数学若是从分数意义的字面定义来突破，过于表层化，学生的学习不应只是表面习得，还应突破知识的本质去获取。由此，学生对一个图形或者一个物体的概念是明确的，对一个整体是模糊的，也就是对“1”的理解是薄弱的，要改变这一现状，就必须从转换“1”的视角开始。

三、探寻教学之“策”

针对以上学生对知识的理解和出现的困惑，笔者在分数意义的教学中努力改变教学着力点，通过转换视角、聚焦单位，从度量的角度将分数理解为“分数是单位的累加”，得出新的思维路径，将为后续的分数学习打下坚实的基础。

（一）凸显单位，深入理解“1”的内涵

课前和学生玩用“1”说一句话的游戏，如8条鱼可以表达为1缸鱼、10根香蕉可以说成1把香蕉等。学生在游戏中发现了很多物体的数量都可以用“1”来表示，自然而然地改变了对“1个”的固有认知。

师：3个苹果能看作“1”吗？怎么看？

生1：把3个苹果圈起来。

师：3个苹果可以看作“1”，6个苹果用多少表示？为什么？

生2：可以用“2”表示，因为有2个“1”。

师：9个苹果呢？

生3：用“3”表示。

上述教学引导学生把3个苹果看作一个整体，并用“1”表示，就是1个单位;6个苹果有2个“1”;9个苹果有3个“1”等。通过转换视角，学生逐渐理解“1”这个单位的内涵。随即可以利用“1个月饼”这一单位，延伸认识几个物体就是几个“1”，再把“1”平均分成4份，其中的1份用[14]表示。

这一视角转换有效打破了学生对“1”的思维定式，充分唤醒了学生对一个整体的已有认知，对“1”的认识不再停留在一个物体和一个图形上，而是从多个角度丰富了“1”的内容。

（二）多元表征，深度挖掘分数的意义

在理解分数概念的过程中，教师要适时引导，让学生自主借助形象、直观的图形或语言来表示分数的概念，并能灵活处理分数概念，巧用对比、精准提炼，促进深度理解。

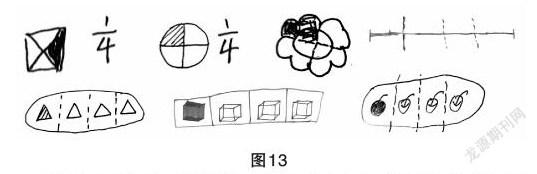
在分月饼的案例中，[14]表示把1个月饼平均分，每份是[14]，学生还用画图或语言描述等方式多元表征，建构[14]这一分数模型。部分学生作品如图13。

从学生的作品及前测的对比中可以看出，转换“1”的视角是有效的，通过不同表征系统的自由切换，同时对这些作品进行对比分析，学生对[14]的理解逐步加强，此时再来提炼单位“1”，进一步丰富了对[14]意义的建构。从[14]延伸到四分之几，再到几分之几，分数的内涵不断深化，学生对分数意义的理解更加深刻。

单位“1”的内涵非常丰富，即一个（一个物体、一个图形、一个计量单位等）、多个（许多物体）、多组（渗透部分与整体、部分与部分的关系），都可以把它们看作一个整体，用自然数“1”表示，通常叫做单位“1”。此外，也要适当扩展它的外延，有不满单位“1”的量，也有几个单位“1”的量，都需要进行区分。

（三）单位累加，深层运用度量去释义

学生常常误解分数总是小于1（比一个蛋糕小、比一个长方形小……），对分蛋糕、分大饼等直观方式，学生容易出现思维僵化。而从字面上看，分数单位是表示其中一份的数。给出一个分数，学生也能说出分数单位是多少，但他们是否真正理解其内涵了呢？

笔者从单位角度出发，借助数轴以[14]为一个度量单位，用[14]依次数出[24]，[34]，[44]，此时的[14]就是一个用来数分数的单位，2个[14]是[24]，3个[14]是[34]，以此类推，不仅数出了真分数，还数出了假分数。[44]是1，再加一个[14]，有5个[14]，就是[54]，这是教学难点，突破了“1”的局限。学生只有跨过了这道“鸿沟”，对分数的理解才更加深入。在数的过程中体会到四分之幾，就是将这样的几个[14]累加而成，有几个[14]就是四分之几。

要度量就要确定度量单位，其核心要素是单位及单位个数。通过数轴对分数作几何解释，这是一个半抽象的模型，也是数学素养的重要组成部分。利用数轴，学生找到[14]这个分数单位，还能依次数出相对应的分数。分数就是通过这样的几个分数单位累加而成，分数的度量意义进一步得到深化，分数的化聚也充分得到了内化，学生从数轴上还能感受真正的分数是密密麻麻地分布在[0，1]区间上，从1开始就是假分数的呈现等。

（四）砌“墙”延伸，深化提升数学素养

特级教师许卫兵说：“思维是数学能力之‘核’，思维也是数学素养之‘魂’。”在以往的教学中不难发现，教师通常一句话就把分数单位概括出来了，但学生对分数单位的理解更多地浮于表面。为了让学生对分数单位、分数的意义有更加深刻的理解，笔者借助分数墙去突破。分数墙就是用长短不一的积木搭成的一堵墙。假设其中最长的积木长度为1，那么其他较短的积木的长度都表示分数单位。用来数分数的单位不是只有[14]，此时把单位“1”依次平均分成2份、3份等，分别找到了[12]，[13]，[14]等单位，分数墙自然而然“砌”成了。学生在对比中发现，这些用来数分数的单位，都是把单位“1”平均分成若干份，并取其一表示某一份。

利用分数墙，学生体会到单位“1”平均分的份数越多，它的每一份就（即几分之一）越少。同时理解了把一张纸条平均分成几份，1份就是这张纸条的几分之一（分数单位），如平均分成6份，1份就是这张纸条的[16]，这张纸条共有6个[16]。在分数墙上能找到一些大小相等的分数，还能发现[22]=[33]=[44]=…=1，等等。这样教学，学生在观察、比较、交流中再次回顾分数单位的产生、感悟单位累加的过程，从中感受到了度量的价值，为后续学习做铺垫，在思维延伸中深化数学核心素养。

总之，在分数意义的教学中，教师要充分理解教材的编写意图，遵循学生的认知规律，转换视角、聚焦单位，巧用度量释义，理解了分数是单位的累加。笔者对分数意义教学的尝试，紧扣内涵本质，降低学生的认知难度，在深度和广度上进行提升，实现对分数意义的理解，在深化数学素养中促进学生的长足发展。

【参考文献】

[1]张奠宙，孔凡哲，黄建弘，等.小学数学研究[M].北京：高等教育出版社，2009.

[2]许卫兵.以思维为核心的数学素养导向[J].小学教学（数学版），2017（1）.

【作者简介】陈 瑛（1985— ），女，江苏南通人，大学本科学历，一级教师，研究方向为小学数学教学。

（责编 杨 春）