小学数学数形结合教学模式的应用研究

曹爽

【摘要】数形结合是小学数学中的重要思想，教师要帮助学生通过观察、推测、合作、探究，获得学习的乐趣，提高数学素养。

【关键词】小学数学;数形结合;策略

一、指导观察，获得启迪

所谓观察就是仔细察看（事物或者现象），它与一般的看有程度上的差别，是对事物或者现象的各个方面、细节进行仔仔细细地看，从而通过表面的、细小的发现，得到一定的启发或者领悟。观察是认识事物、获取知识最基本的手段。学会观察，是学生自主获得知识、培养能力的必由之路。教师要以学生为主体，培养他们观察的良好习惯以及善于观察的能力，从而为他们的终身学习打下坚实基础。

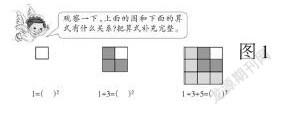
观察的方法很重要，教师要指导学生从图形的数量、颜色、顺序以及图形和算式的对应关系等方面进行观察，从而让学生顺利地掌握观察的方法，获得思维的启迪。如从图1可以观察到以下信息：图形从左向右，由1个小方块变成了4个再增加到了9个;从颜色上观察，白色小方块的位置始终没有改变;而第二个图形中在白色小方块的左下方多了深色的三个同样大小的小方块;第三个图是在第二个图的基础上又多了5个同样大小的浅色小方块。

在观察中，教师可以进行必要提示，如1+3等于4，4是数字几的平方呢？1+3+5等于9，9又是数字几的平方呢？数字2和3与上面对应的图有什么关系呢？这样的引导可帮助学生深入观察数形之间的关系，从而启发学生：算式之和正好是大正方形的面积，是构成大正方形的小正方形的面积之和，也是正方形每行（列）个数的平方，还是这个算式中连续奇数个数的平方。

二、大胆推测，发展想象

教学中，教师还要引导学生进行大胆推测，培养学生合理的想象能力，获得数学学习的乐趣。推测与胡思乱想有着本质的区别，胡思乱想是没有根据的空想，而推测是根据已知来猜想未知。在学生已经发现了数形之间的联系后，可引导学生通过想象，获得一般性的规律。

例如____=92这一算式，根据所学，对应的图形应该怎么画？横线上的算式又该怎么填？学生经过刚才的观察，明白了要在面积为9的正方形的右侧和下侧继续添加小正方形，即分别添加7、9、11、13、15、17个，构成边长为17的大正方形。横线上应该填1+3+5+7+9+11+13+15+17。通过这样一种推测，学生的思维被引向了更加广阔的空间，学生的想象能力得到了发展。许多教师并不喜欢引导学生进行推测，而是简单地让学生通过数数填寫，脱离了对图形的想象，学生获得的直观感受受到限制，数形结合的思维没有得到有效发展。

三、合作学习，集思广益

数形结合的题目，有时靠一己之力不能很好地解决，这时就要发挥集体的力量，通过小组合作探究让数学课堂生机勃发、趣味无穷。

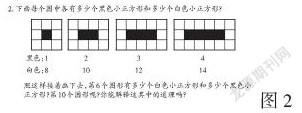
例如，教材第108页的这道题（如图2），题干中呈现了四幅图，图下面分别罗列出黑色、白色正方形对应的个数，求“照这样接着画下去，第6个图形有多少个白色小正方形和多少个黑色小正方形？第10个图形呢？你能解释其中的道理吗？”。看上去这道题也可以通过继续画的方法解答，但是要画到第10个图形显然不太容易，而且题目要求解释其中的道理。课堂上，要充分发挥学生的学习能动性，让学生通过小组合作进行充分讨论。小组成员各司其职，组长负责分配任务，讨论员积极讨论，记录员认真记录讨论过程和结果，汇报员踊跃发言，辩论员补充发言。经过小组讨论发现，每幅图中黑色方块每增加1块，白色方块就增加2块，可是又很难用一个算式来表示。

教师一方面要肯定学生善于观察，另一方面继续引导学生：还有没有其他的发现？这时候学生讨论的热情更加高涨。有小组通过讨论发现四幅图画不变的地方就是，不管黑色小方块如何增加，两边共6个白色小方块的个数始终没有变化;还有小组讨论发现，变化的只是每一幅图中上下白色小方块的个数，而且发现该个数正好是黑色方块的2倍。教师继续引导：如果把黑色小方块的个数标作n，那么每幅图的白色小方块的个数就可以怎么表示？这时候，学生就懂得用“n×2+6”来表示了。

在整个学习过程中，教师充分尊重学生的学习主体地位，让他们通过观察、思考、讨论，形成探究性学习;教师发挥组织、引导作用，引导学生不断“探骊”，最后“得珠”。学生从图形出发，思考黑白两种图形个数之间的联系，通过探究不断提炼两者的数量关系，最后找出了图形中隐藏的规律，发展了数形结合思维。

四、深入探究，其乐无穷

数形结合，或通过数（算式）找出对应的图形，或探究出图形中隐藏的数学规律，可使学生从中发现数学学习的趣味，获得成功感。而数形结合不应满足于一种、一式，形式变化无穷，其乐亦无穷。在具体的教学过程中，教师应提供各种类型的数形结合题，帮助学生由此及彼，由浅入深，探寻无穷无尽的数学乐趣。

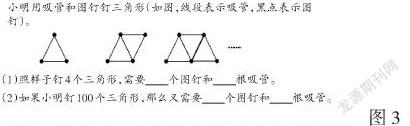
例如，探究图3中的题目时，学生发现每增加一个三角形，图钉就增加一个，而吸管却增加了2根;增加的图钉是新三角形的顶点，增加的吸管是新三角形的两条边。探究到了这里，教师相机引导，让学生把这些内容以表格的形式呈现出来，然后继续探究，看看还有什么发现。

学生比较“三角形的个数”“线段的条数”“三角形顶点的个数”三个变量之间的关系，假设三角形的个数为n，线段的条数除以三角形个数是2余1，三角形顶点的个数比三角形的个数多2，这样就可以用2n+1、n+2来分别表示线段的条数和顶点的个数了。学生探究到这样的结果后，就会产生强烈的满足感和成功感。

总之，“教学思有路，遵路识斯真。”在数学教学过程中，教师要尊重学生认知的一般规律，激发学生学习的积极性，引导学生通过观察、推测、合作和探究，提升由浅入深、循序渐进的能力，从而有效提高学生的数学素养。