优化概念教学促进深度学习

张莉莉

[摘 要]结合教学实践，从导入、操作、变式、应用四个方面探讨数学概念教学中促进学生深度学习的基本策略，使深度学习理念在数学课堂上“落地生根”。

[关键词]概念教学;深度学习;引入;操作

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）02-0041-02

目前，小学数学概念教学存在诸多问题，如重视结论、轻视探索，重视课本、轻视实践。教师在教学中往往直接把结论告知学生，没有让学生逐步探索，导致学生对概念认识不深刻，缺乏求知、探知的欲望。如果教师在课堂上对概念进行呈现、讲解后，止步于理论，不能把概念与现实生活联系起来，还会导致概念教学脱离实际生活，变得枯燥乏味，难以吊起学生的“胃口”。如何使概念教学摆脱单调低效的窘境呢？深度学习理论为我们开启了一扇新窗。深度学习理论侧重于学生对知识的理解、探索、融合和应用，是一种理论与实践并重、过程与结果齐进的学习理念。基于此，笔者主要从导入、操作、变式、应用四个方面探讨数学概念教学中促进学生深度学习的基本策略，使深度学习理念在数学课堂上“落地生根”。

一、情境导入，让数学概念不再“冷冰冰”

在概念教学中，生动的情境能够充分提高学生探索问题的主动性，激发学生的创造性思维。教师在创设情境时，要融入生活气息，拉近数学概念与现实生活的距离，使学生产生亲近感，进而为深度学习奠定基础。

【教学片段1】 分数的意义

师：星期天，淘气、笑笑和乐乐去蛋糕店买蛋糕，一个蛋糕需要10元钱，可是淘气只带了5元钱，笑笑只带了3元钱，乐乐只带了2元钱。他们各自带的钱都不够，那怎么办呢？

生1：他们的钱加起来刚好可以买一块蛋糕，他们可以合买一块啊！

师：你真聪明。他们三人拿出自己带的钱合买了一块蛋糕。但是，他们应该如何分这块蛋糕才公平呢？

生2：把蛋糕切成3块，一人1块。

生3：这样不行，淘气拿的钱最多，这样对淘气不公平。

生2：那应该按照拿钱的多少来分蛋糕。

师：对。按照拿钱的多少来分蛋糕最公平，要做到这一点，就需要用到分数。现在，就让我们一起走进奇妙的分数王国吧！

数学概念具有很强的抽象性，因此，在概念教学中要实现学生的深度学习，把抽象的数学概念融入生动的现实情境尤为重要。在教学中，教师把“分数的意义”蕴藏于“分蛋糕”的故事情境之中，极大地拉近了抽象概念与现实生活的距离，使学生认识到数学概念并非仅存在于课本上，更是解决实际问题的现实需要，从而使学生产生“一探究竟”的欲望。

二、数学操作，让抽象概念“外显于行”

數学概念的形成是一个从直观到表象，最后再上升为抽象的过程。教学中，教师可借助直观操作把抽象的数学概念生动地展示出来，引导学生在操作的过程深刻理解抽象的数学概念，培养学生的实践操作能力和逻辑思维能力，达到“外显于行，内化于心”的效果，最终实现深度学习。

【教学片段2】长方形的面积

师：这是一个长4厘米、宽3厘米的长方形，如何求得它的面积呢？

生1：可采用摆小方块的办法。

（学生操作，教师巡视指导）

生2：我用纸剪出了长和宽都为1厘米的小正方形，它的面积是1平方厘米（展示测量工具）。我把小正方形平铺在长方形中，发现每一行可以放置4个小正方形，一共放置了3行，所以一共是4×3=12（个）小正方形，因此，长方形的面积是12平方厘米。

生3：这个方法不错，可以准确地测量出长方形的面积。但是需要12个小正方形，比较麻烦。我也是用了平铺的办法，但是我只用了一个小正方形就测量出了长方形的面积。我先用一个小正方形横着比对，发现每一行需要4个小正方形，再用这个小正方形竖着比对，发现每一列需要3个小正方形。由此我得知，要铺满整个长方形，需要4×3=12（个）小正方形，长方形的面积是12平方厘米。

师：这两位同学都用了平铺法。但是，哪个办法更简便些呢？

生4：生3的办法更简便，这样就不用剪出那么多的小正方形了。

师：这两位同学的操作过程虽有差别，但是最后都得出4×3=12（个），这个“4”和“3”各代表什么呢？

生5：长方形的长是4厘米，所以它的每一行就需要4个小正方形才能铺满;长方形的宽是3厘米，所以它的每一列就需要3个小正方形才能铺满，这样就需要4×3=12（个）小正方形。

师：看来，“4”指的就是长方形的长，“3”指的就是长方形的宽。那么，我们就可以得出长方形的面积等于长乘以宽。

上述教学中，学生在直观操作中实现了对概念的深度理解，这主要得益于两个方面：一是操作过程的优化;二是在操作中理解。学生尽管通过平铺法已经测出了长方形的面积，但是对知识的认识不能止步于此，学生在分析操作中得出“4”和“3”分别代表什么含义，就能把直观操作上升为抽象概括，实现学生对知识的深度理解，最终得出长方形的面积公式。

三、巧用变式，让数学概念更“精准稳固”

为了适应小学生的认知水平，教材在定义一个数学概念时往往简单地表述为“像……具有……的……，叫作……”，不可否认，这种相对直接的表述方式对于学生理解概念有很大帮助，但是也不可避免地造成学生对概念认知的固化和模式化，从而形成思维定式。因此，在概念教学中，恰当运用变式材料，能够丰富学生认知，打破学生的思维定式，进而实现学生对概念的深度理解。

【教学片段3】 梯形的定义

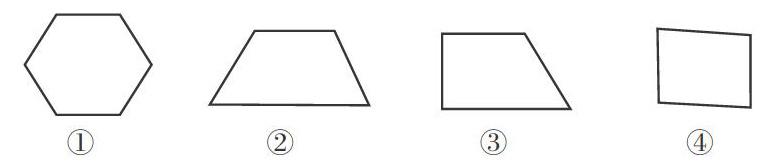
师：下面的图形，哪个是梯形，哪个不是梯形。

师：在判断之前，我们先来说说什么是梯形。

生1：只有一组对边平行的四边形是梯形。

生2：①不是梯形，它是个六边形，不是四边形。

生3：②不是梯形，它的确有一组对边平行，但是另外的两边是相等的。

生4：不对，②也是梯形。它满足梯形的定义——只有一组对边平行的四边形。

师：对，②是梯形。两腰是不是相等并不是梯形的本质属性，不会影响对梯形的判定。

生5：③是梯形，它满足梯形的定义。

生6：但是它有两个角是直角，这也是梯形吗？

师：③也是梯形，只要满足只有一组对边平行的四边形这个条件，就是梯形，是不是有两个直角不会影响对梯形的判定。

生7：④不是梯形，它两组对边都平行，不符合梯形的定义。

上述教学中，学生之所以会对梯形的判定产生疑问和分歧，主要是无法排除梯形非本质属性的干扰。教师应引导学生把握梯形的本质属性，即只有一组对边平行的四边形，并且排除非本质属性的干扰，比如两条腰的长短，是不是有两个直角等，这些并非梯形的本质属性，并不会影响对梯形的判定。巧用变式打破了学生的定式思维，开阔了学生的思路，促进了学生对梯形概念的深度认知，使学生对梯形的本质认识更加精准稳固。

四、重视应用，让概念在现实中“活起来”

深度学习是一种理论与实践并重的学习理念，它的目的是要通过知识学习构建一种解决实际问题的方法，因此，实现对概念的深度学习就不能忽略概念的实际应用环节。只有实现了数学概念的活学活用，才是从根本上落实了深度学习理念。基于上述认识，教师引导学生从直观、表象到抽象理解概念的同时，也要引导学生从抽象转向现实，实现概念的灵活运用，从而加深知识理解，树立应用意识。

【教学片段4】比例尺

师：新民广场有一个巨大的正方形花池，笑笑把这个花池画在一张图纸上（比例尺为1∶500），从图上量得正方形花池的边长是4厘米，那么，花池的实际周长是多少米？

生1：根据“图上距离÷实际距离=比例尺”可以得知，实际距离=图上距离÷比例尺，那么，实际距离=4÷[1500]=2000（厘米），2000厘米=20米，所以正方形花池的周长=20×4=80（米）。

生2：我是这样做的。1∶500说明图上1厘米表示实际距离500厘米，那么由图上距离4厘米可得实际距离就是4×500=2000（厘米），2000厘米=20米，所以正方形花池的周长=20×4=80（米）。

生3：生2这个方法的运算思路更清楚，理解起来也更简单。

生4：看来比例尺在生活中很有用呢。

师：对，比例尺的应用非常广泛，尤其在绘图中，掌握比例尺的运算更是一项必不可少的技能。

上述教学中，教师紧密联系實际生活设计题目，使学生体验到利用比例尺的知识解决实际问题的优势，在实际应用中进一步内化相关知识，把课本理论知识与现实生活中的问题紧密结合起来，进一步深化了学生对知识的理解。

总之，从导入、操作、变式、应用等视角优化概念教学，是实现深度学习的有效途径。值得一提的是，教师在应用这些方法优化概念教学时，要结合数学概念的内容，或重操作，或重变式，或重归纳，或重应用，只有灵活运用这些方法，才能达到优化教学过程、促进深度学习的目的。

（责编 黄春香）