基于重力异常特征点的等轴状场源中心埋深自动化估计算法

张 攀，杜劲松,2，邱 峰

(1.中国地质大学 地球物理与空间信息学院 地球内部多尺度成像湖北省重点实验室，湖北 武汉 430074；2.中国地质大学 地质过程与矿产资源国家重点实验室，湖北 武汉 430074)

1 引 言

在重力勘探中，特征点法是根据重力异常曲线上的一些特征点(如极大值点、1/n极值点、零点、拐点等)(其中n>1)的重力异常值以及它的相对坐标位置求取场源的几何参数和物性参数的一种方法[1,2]。

当地质体的最大与最小延伸尺度之差ΔL与最小埋藏深度D满足ΔL<0.2ΔD时，可将场源近似为球体。在实际应用中，盐丘、矿囊、岩体等近似等轴状的地质体均可以等效为球体进行处理。本文根据特征点法的特点，设计自动化算法，当输入是一个二维的重力数据时，首先自动找出异常极值点，其次判断其是否为等轴状，然后对反演可用的1/n极值点范围进行搜索，挑取多个1/n极值点进行特征点法深度反演，最后对反演结果进行分析，确定最终结果。随后，将该算法分别应用于模型数据中，得到了比较精确的结果，在加噪声的模型数据和实测数据中也得到了良好的结果[3-8]。

2 自动化反演方法

2.1 特征点反演方法

对于一个各向同性的均匀球体来言，其引起的重力异常与同质量的点源引起的重力异常是完全相同的[10-14]。将球心在地面的投影处记为O点，由于球体具有对称性，只需研究通过O点的任意一个方向的剖面重力异常即可，离O点的距离为x的一点处的重力异常Δg，单位 m/s2，计算表达式为

(1)

式中，D为球体中心的埋藏深度，单位 m；ΔM为球体的剩余质量，单位t；x为测点离球心在地面的投影O点之间的距离，单位 m；G为万有引力常数(6.672×10-11N·m2/kg2)。

在异常曲线上任意取出两个点，设它们的坐标为x1和x2，相应的异常值为Δg1和Δg2，则根据式(1)可得

(2-1)

(2-2)

将上式求比值以消去G和ΔM，将其比值记为w，则

(3)

进而，可以推导得到中心埋深D的显示表达式为

(4)

对式(4)进行简化，令x1=0，在此处异常具有极大值，即Δgx1=Δgmax，设x2为1/n极值，则有

(5)

(6)

式(5)和式(6)即为球体中心埋藏深度的反演计算通式。

在得到球体中心埋藏深度之后，若已知剩余密度Δσ，单位 g/cm3；进而可以得到球体的剩余质量ΔM、半径R、上顶埋深hu、下底埋深hl分别为

2.2 自动化算法

2.2.1 极值点搜索

平面重力数据为一个二维的数组，在寻找极大值时，先预分配两个大小与原始数组相同的零矩阵[15-18]，记其为A1和A2。首先沿着数组的每一行进行极大值的搜索，如果当前位置的值为极大值，则将A1中相同的位置标记为1，之后沿着数组的每一列进行极大值的搜索，如果当前位置的值为极大值，则将A2中相应的位置标记为1，最后将A1和A2进行点乘，其结果记为A。在A矩阵中，1出现的地方即为平面数据中极大值点的位置。

但是，在数据含有一定的噪声时，这种标定方法会将所有噪声造成的小突或凹点均标定出来。为了解决这个问题，本算法在标定极值的过程中引入了三种判定准则。

1)当标定的极值的绝对值小于一定的阈值之后，则舍去这个标定出的极值；

2)以极值为中心取一个滑动窗口，如果该极值的绝对值不是当前窗口中的最大值时，则舍弃不采用，滑动窗口的大小视具体情况而定；

3)重力异常主体如果一部分在边界之外，则不适合进行特征点法反演，则对离边界很近的一些极值点不进行标定。

通过这三种准则的约束，即使重力异常数据存在一定的噪音，也能对数据中的极大值点进行准确的标定。

2.2.2 判断异常是否为(似)等轴状

以标定出的极大值点为中心，沿N个方向获取N条剖面，在这N个方位通过线性插值寻找1/n极值点，在正常情况下，将会搜索到2N个1/n极值点，在本算法中，引入两种评价标准用于判断异常是否能近似为等轴状。

1)对这2N个1/n极值点的位置进行椭圆拟合[3]，求出它们组成的椭圆的离心率，若离心率过大，则证明该异常不能近似为等轴状；

2)根据2N个1/n极值点距离极值点的距离，求出距离的极差，由于重力异常有大有小，极差不能进行比较，则将极差与距离的最大值进行比值计算，将其定义为相对极差，若相对极差较大，则证明该异常不能近似为等轴状。

如果异常比较特殊，沿某一个方向没有搜索到1/n极值点，则直接将异常认定为非等轴状异常。这一步可以选择一个1/n极值点或者多个1/n极值点进行综合评价。经过这一步，数据中的非等轴状异常则会被排除，而不参与后面的反演计算。

2.2.3 确定反演的1/n极值点

在这个环节，需要挑选多个1/n极值点共同反演，最后的结果挑选比较可靠的一部分进行均值计算。设起始搜索的1/n极值为1/n_start 极值，截止搜索的1/n极值为1/n_end 极值。

n_start的选取准则为：极值与1/n_start 极值之间的距离不能小于测点平均点距。令n从n_start开始，步长为dn，不断地增大n，并且求出当前搜索到的1/n极值拟合椭圆的离心率和相对极差。本算法引入四种判断准则来确定n_end，如下：

1)如果没有搜索到当前的1/n极值，则在前一个步长停止；

2)如果当前搜索到的1/n极值拟合椭圆的离心率过大，则证明异常当前的形态已经不符合等轴状的特征，则在前一个步长停止；

3)如果当前搜索到的1/n极值的相对极差过大，则证明异常当前的形态已经不符合等轴状的特征，则在前一个步长停止；

4)如果当前搜索到的1/n极值小于3倍的观测数据误差标准差，则在前一个步长停止。

2.2.4 在n_start 到n_end范围内进行特征点法深度反演

将n_start到n_end范围中每条剖面取出M个1/n极值点进行特征点法深度反演，得到N×M个深度点，同时求出当前1/n极值搜索到的1/n极值点的拟合椭圆的离心率和距离的相对极差作为结果是否准确的评判标准。

沿每条测线得出的深度值可能不同，若直接将结果进行平均计算，则一些由噪声引起的“奇异值”会影响结果的准确性。为了解决这个问题，本算法在这一步引入了离散系数Vs作为评判准则，离散系数的定义为：

(8)

3 模型试验

3.1 简单模型试验

设计点源质量为3×1011kg，中心点埋深为1 000 m。数据共201条测线，每条测线上面具有201个采样点，数据的点距和线距均为100 m，正演得到地面上的重力异常，如图1所示。

将模拟数据输入算法，先后经过极值点的搜索、异常是否为等轴状的判断、反演范围的搜索以及反演。在计算过程中，总共沿四个方向均匀的拉出四条剖面，将n_start到n_end范围中均匀取出30个1/n极值点进行特征点法深度反演，n_end的截止最大值为6，计算结果如图2所示。

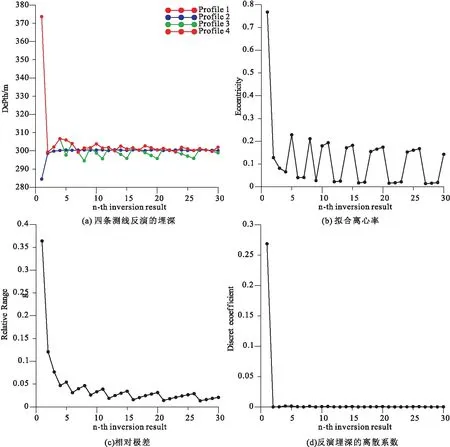
图2 反演结果Fig.2 Inversion results

将所有的反演结果直接进行平均，得到的深度反演结果为1 004.4 m，相对误差为0.44 %。根据式(5)可见，若n值较小，可能引起埋深偏大。因此，根据离散系数，将第一个反演深度数据舍去之后再求平均，得到的深度反演结果为1 001.2 m，相对误差降为0.12 %，结果也更为准确。

3.1.1 噪声的影响分析

对于实际数据，其不可避免地会含有噪声干扰。为了更好地符合实际情况，将上述重力数据中加入一定量的噪声再进行计算，用于检验算法的稳定性。由表1所示，由于每次加入的随机噪声幅度不同，计算结果也存在差异。可以发现，随着噪声的增大，结果的相对误差总体上呈现出增大的趋势，而且计算结果的离散系数也呈现出增大的趋势。虽然算法显示具有比较稳定的性能，但是在实际应用之前，还是建议预先对实测数据进行适当的去噪处理。

表1 添加不同幅度噪声情况之下的反演结果

3.1.2 背景场的影响分析

特征点法具有其应用条件，该方法是基于单个异常体的重力异常表达式推导得出的，而实测异常是多个异常体叠加而成的，一般也含有背景场，致使极值和1/n极值点之间的相对关系就会发生变化，故运用特征点法之前必须去除背景场。但是，在实际应用中，目前的位场分离技术并不能完美地将局部场和背景场分离，或多或少还是会存在一定的剩余。因此，为了更好地符合实际情况，将上述重力数据中加入背景场进行计算，用于分析背景场对特征点算法的影响。

在前述模拟的重力异常数据中加入不同的常值作为背景场，计算结果如表2所示。如果加入背景场的数据为正值，则随着1/n极值中n的增大，反演的深度会越来越大；如果加入的背景场的数值为负值，则随着1/n极值中n的增大，反演的深度将会越来越小。当背景场幅度为局部异常幅值的10 %时，反演埋深的相对误差可达18 %左右。因此，背景场对于反演深度结果的影响非常大，建议在实际应用之前，采用不同位场分离技术，进行综合判断。

表2 不同背景场下的反演结果

表3 不同非等轴状场源的反演结果

3.1.3 场源非等轴状的影响

在实测重力异常数据中，很少能够找到完美的等轴状异常。为了更好地符合实际情况，将非等轴状场源正演得到的重力异常数据输入算法进行测试，用于分析场源非等轴状的影响。

采用宽与高分别为1 000 m与1 000 m，剩余密度为0.4 g/cm3，埋深为2 000 m的直立棱柱体作为场源，不断改变棱柱体的长，最后得到的反演深度结果如表3所示。可以看出，场源非等轴状对反演深度造成的影响很大，当长宽比超过2∶1之后，反演深度的相对误差会超过7 %。因此，在实际数据反演时，必须结合离心率和相对极差评判结果的可靠性。

3.2 组合模型实验

对于实测重力异常数据，往往包含多个异常。因此，设计组合模型实验，采用两个点源模型模拟等轴状异常，采用一个棱柱模型模拟非等轴状异常。第一个点源质量为3×1011kg，中心埋深为2 000 m；第二个点源质量为1.2×1011kg，中心埋深为700 m；采用的棱柱模型的长宽高分别为5 000 m、200 m、40 m，中心埋深为700 m；三个模型的剩余密度均为0.4 g/cm3。模拟得到的重力异常如图3所示。

图3 组合模型模拟的重力异常Fig.3 Synthetic gravity anomaly by combined density models

首先进行重力异常极大值点的标定，接着在极大值附近搜索1/5极值的位置用于椭圆拟合和相对极差的计算。经过计算，左上角非等轴状异常的拟合离心率为0.894 7，右上角等轴状异常的拟合离心率为0.191 4，下方等轴状异常的拟合离心率为0.127 8；左上角非等轴状异常的相对极差为0.566 9，右上角等轴状异常的相对极差为0.041 8，下方等轴状异常的相对极差为0.016 3。可见，左上角的重力异常的离心率和相对极差均较大，因此舍去该异常不对其进行后续反演。

之后，对标定出的异常进行反演范围的搜索和深度反演，得到下方相对宽缓的等轴状异常的深度为2 011.0 m，相对误差为0.55 %，根据离散系数将一些不稳定结果剔除之后，得到的反演深度为2 007.0 m，相对误差为0.35 %；右上角相对尖锐的异常的深度为704.2 m，相对误差为0.60 %，同样根据离散系数将一些不稳定结果进行剔除，最后得到的反演深度为702.8 m，相对误差降为0.40 %。

组合模型试验表明，对于拥有多个等轴状和非等轴状异常的数据，算法可以挑选出等轴状的异常并且进行反演，反演结果也较为准确，从而证明了本文算法的可行性。

4 实际应用

将上述算法应用于位于美国路易斯安那州的Vinton盐丘，测区位于路易斯安那州与德克萨斯州交界处，测区以南即为著名地石油产地墨西哥湾。测区多为沉积岩，底部发育盐丘构造，盐丘区经常形成油气圈闭，因此对盐丘进行研究具有实际意义[4，5]。

图4 Vinton盐丘重力异常Fig.4 Gravity anomaly of Vinton salt dome

文中使用的数据为航空重力测量数据，总测线长度为1 087.5 km，测区面积为192.6 km2，数据的点距和线距均为30 m，地形改正密度值为1.8 g/cm3。本文截取面积为61 69 m×6 169 m的具有目标重力异常的区域(图4)，使用本文算法进行埋深估计，进而与前人计算结果进行对比。

由模型试验可知，噪声以及背景场对反演计算均会产生一定的影响。因此，首先采用递归滤波方法，截断波长设置为294.19 m，补偿系数为1，对Vinton盐丘重力异常数据进行了去噪处理，结果如图5所示；然后，采用匹配滤波法，分频点波长设置为5 589.68 m，对去噪之后的重力异常数据进行局部场和趋势场分离，结果如图6所示。

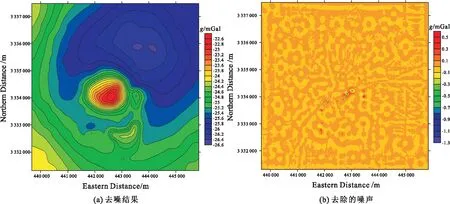
图5 Vinton盐丘重力异常去噪处理Fig.5 Noise reduction for gravity anomaly of Vinton salt dome

图6 Vinton盐丘重力异常位场分离结果Fig.6 Potential field separation for gravity anomaly of Vinton salt dome

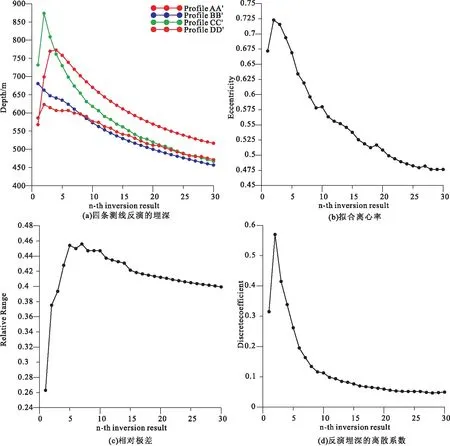
图7 反演结果Fig.7 Inversion results

表4 本文与前人反演的Vinton盐丘几何参数

计算得到的结果如图7所示。设盐丘的密度[6,10]为2.7 g/cm3，选取离散系数小于0.1的计算结果。表4对比了本文与前人反演的Vinton盐丘的几何参数，对比显示本文所得中心与上顶埋深与前人计算结果一致，但是下底埋深大于前人结果。邱峰等(2020)[17]认为该盐丘的构造指数为1.198，其形态比较接近于柱体状而非球状(球体的构造指数为3)，重力异常由盐丘高密度、扁平的盖层引起而非盐丘本身。场源的非等轴状导致本文计算所得的下底埋深偏大。

5 结 论

本文将重力勘探中的特征点反演方法进行了计算机自动化处理，使其能够识别重力异常平面数据中的(似)等轴状异常，进而进行场源中心埋深反演与误差统计，并且输出拟合离心率、相对极差和离散系数作为评价结果准确性的参数。

理论模型试验表明，数据包含的噪声对反演结果存在一定的影响，但是影响较弱，而背景场对反演结果影响较大。因此，建议在实际反演之前，对实测数据进行适当的去噪与分场处理。此外，理论模型试验显示，本文算法可以准确地找出数据中的(似)等轴状异常，并且比较准确地计算得出异常体的中心埋深。将本文算法应用于美国路易斯安那州的Vinton盐丘的航空重力数据，得到了较好的结果，与前人计算埋深一致。理论模型试验和实际应用均证明了本文算法的可行性与实用性。

致谢

感谢美国Bell Geospace公司提供Vinton dome地区的重力异常数据！