考虑渗透系数各向异性的盾构隧道开挖面稳定性数值极限分析
2021-01-08冯德旺
袁 帅,冯德旺
(长安大学公路学院,陕西西安710064)
随着社会的发展,城市人口增加,许多城市开始大规模兴建地下轨道交通来缓解交通拥堵问题。目前,城市地铁隧道普遍采用盾构法施工,盾构掘进过程中密封舱支护力不足会引起开挖面的坍塌,支护力过大则会引起地面隆起,因此,开挖面支护力的合理确定对保证盾构隧道安全施工非常关键。城市隧道围岩失稳大都与水有关,隧道开挖改变周围地层水力环境,引发地下水渗流,使得围岩力学性质弱化,增加盾构隧道开挖面失稳的风险。因而,开展复杂水力环境下盾构隧道开挖面稳定性研究具有重要的理论及实际意义。
近年来,各种方法如理论分析、模型试验和数值模拟等在盾构隧道开挖面稳定性分析中取得了非常广泛的应用。在这其中,极限分析方法得到了大量的应用,在这其中又以上限法居多。Leca等[1]构造了砂土地层隧道开挖面三维锥形体破坏模式。Soubra[2]在锥体之间进行过渡圆滑,对锥形体破坏模式进行了改进。Subrin[3]提出了一种“牛角状”破坏模式,并通过数值及实验方法进行了验证。Mollon等[4]构造了三维平动多块体集,研究了盾构隧道开挖面稳定性问题。宋春霞等[5]考虑土层的非匀质性,构造了平面应变隧道刚体平动破坏模式,应用多块体上限法进行研究。数值极限分析方法的应用则相对较少,Sloan等[6]利用有限元上下限分析方法分别研究了浅埋隧道围岩及开挖面稳定性,考虑了地层土体不排水抗剪强度随深度的线性变化。杨峰等[7]应用上限有限元法分析了平面应变条件下隧道开挖面稳定性,并与多块体上限法进行了对比。
隧道开挖会导致开挖面附近孔压场发生改变,引起地下水渗流,因此有必要在极限分析中考虑孔压的影响,使用有效应力强度参数。基于Leca[1]提出的三维破坏机制,Lee和Nam[8]在上限计算中考虑了地下水渗流的影响,将极限支护力分为两部分:有效应力部分和渗透压力部分,并且指出,渗透压力的部分会远远大于有效应力部分。在后续工作中,Lee和Nam[9]研究了隧道开挖速率对开挖面稳定性的影响。黄阜等[10]研究了地下水渗流对浅埋隧道开挖面安全系数的影响。Liu等[11]分析了成层土中渗透力对开挖面稳定性的影响。吕玺琳等[12]研究了水位变化对盾构隧道开挖面孔压分布特性。郑佳艳等[13]分析了高水压条件下盾构隧道开挖面稳定性。宋曙光[14]研究了复合地层盾构施工开挖面失稳机理和渗流作用下开挖面失稳破坏演化特性。汤军旅[15]研究了稳态渗流饱和砂性土地层盾构开挖面稳定性问题。
然而,现有工作大都将开挖面周围土体的渗透特性视为各向同性以简化计算。众所周知,土在沉积的过程中由于各种因素的影响会产生各向异性,即土体的应力及渗透特性与所选取的方向有关。土体渗透系数的各向异性已经被广泛证实,学者们也逐渐认识到渗透系数对岩土工程结构力学特性的重要影响。梁燕等[16]研究了原状黄土的渗透系数各向异性特征及其机制。杨林德等[17]在考虑地下水渗透各向异性和土体内Biot有效应力分布的各向异性的条件下,推导出一个地下水渗流耦合作用的有限元计算公式。何秉顺等[18]基于有限元法和条分法分析了土坝在各向异性渗流场下的稳定性。关于渗透系数各向异性对隧道开挖面稳定性的影响分析则非常有限,值得进一步的深入研究。本文结合渗流分析和数值极限分析方法,研究渗透系数各向异性对盾构隧道开挖渗流场及开挖面极限支护力的影响,分析渗透力所导致开挖面破坏机制的变化,为盾构隧道安全施工提供重要的参考。
1 数值极限分析方法
1.1 上限分析理论
假定一刚性理想塑性体Ω受到体力λg及面力λT的作用,其中g和T为事先给定的分布,λ为所要优化的载荷乘子。在给定速度边界Γu上指定速度的大小。上限理论可以表述为:如果可以找到满足运动和塑性许可的速度场,该速度场满足变形协调关系、速度边界条件和塑性流动法则,则极限荷载的上限可以通过外力功和内力功相等来得到。上限分析定理的数学描述为

式中:Wint为内功率,Wext为外力功率;D(ε˙)为塑性耗散函数;u˙和 ε˙分别为速度场和应变率。在实际问题中经常采用上限定理的对偶形式或称为基于应力的上限定理,则maximize λ
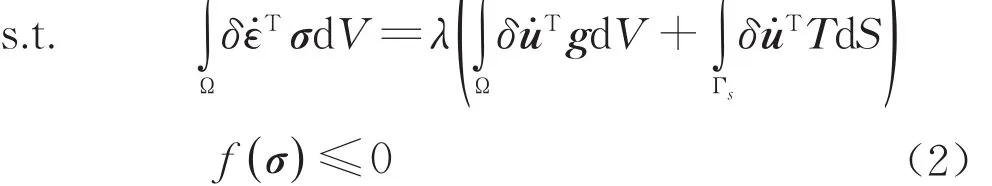
式中:σ为应力;f(σ)为屈服函数。对偶形式所需的优化变量更少而且不容易出现线性相关等式约束。因此,本文基于上限定理的对偶形式建立相应的数值方法。
上述上限定理形式中没有考虑孔隙水压的影响,为了研究渗流作用下土工结构的稳定性,引入有效应力原理即

式中:σ′为有效应力;uw为孔隙水压力。将式(3)代入式(2)后可得
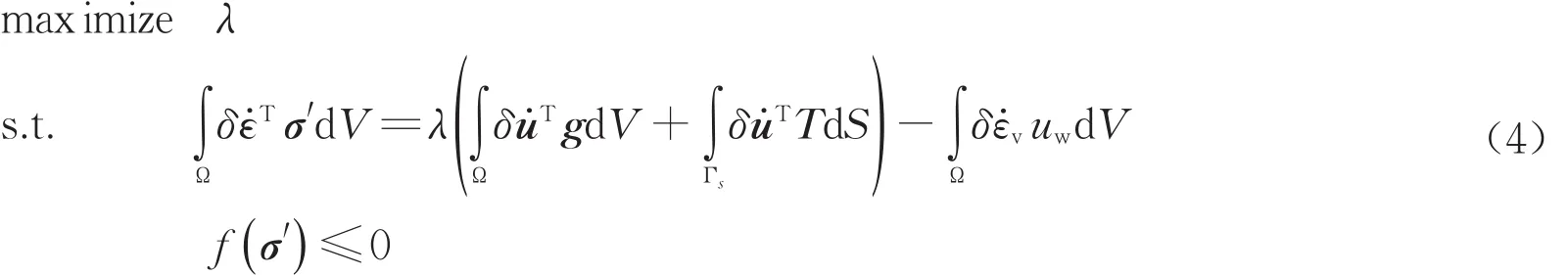
1.2 空间离散
为了克服体积闭锁问题并且提高现有单元的计算效率,Makrodimopoulos 和Martin[19]提出了一种线性应变单元,只要单元的所有边都是直边就能保证所得到的结果是严格的上限解。正如图1所示,速度结点位于四面体的顶点和各边的中点,而应力结点只位于四面体的顶点。速度结点由相邻单元共享,而应力结点则只属于某个特定的单元。单元内的速度场可以表示为


式中:Li为角点所对应的体积坐标;Nε为包含应变型函数的系数矩阵;ε˙e为单元应变矢量。相应地,四面体内的应力矢量可以表示为
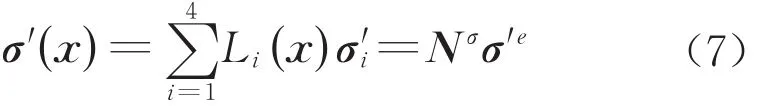
式中:Nσ为包含应力形函数的系数矩阵;σ′e为单元应力矢量。将式(6)代入式(5)后可得

式中:B 为应变矩阵。将式(8)代入到式(4),简化后得

图1 上限分析线性应变单元Fig.1 Linear strain element in upper bound analysis

式中:σ′g为整体有效应力矢量;q为整体载荷矢量;q0为整体给定力矢量;qw为整体孔隙水压力矢量;Ne为单元个数。
1.3 半正定锥规划
假定土体满足摩尔-库伦强度准则,以主应力表示为

式中:σ′1和σ′3为大、小主应力,c′和φ′分别为有效黏聚力和有效内摩擦角。三维条件下摩尔-库伦模型则可以转化为半正定锥的形式,采用半正定锥规划对非线性优化问题进行求解。半正定锥定义为
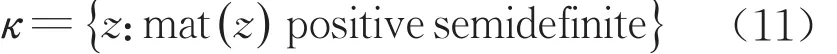
式中:“mat”为一矩阵算子,mat(z)表示将矢量z转换为对称二阶矩阵。这里引入符号Z,即

Z定义为

另外定义

表示Z为一个半正定对称矩阵。引入符号

摩尔-库伦强度准则可以表示为半正定锥的形式[20]

式中:β为引入的辅助变量;I为单位矩阵;a和k由下式可得

最终的数学规划问题为

式中:m=[1 1 1 0 0 0]T为单位辅助向量。
式(18)将通过Mosek的Matlab工具箱进行求解。
2 开挖面稳定性分析
2.1 问题描述
盾构隧道开挖示意图见图2,隧道截面为圆形,直径为D,埋深为C,地表水位为Hw,假定开挖面上施加均匀的支护力,当支护力小于某个极限值plim时,开挖面附近土体会发生失稳,该极限值称为极限支护力。由于隧道开挖改变了周围岩土体的水力环境,导致周围孔隙水流入隧道,由于渗透力的存在,开挖面所需支护力大大增加。计算中所用到的典型计算模型及网格划分如图2b所示,计算模型取足够大以减小边界条件对计算结果的影响。为了简化计算,假定渗流达到稳态,开挖面为完全排水边界,孔隙水压力为零,给定地表孔隙水压力,且不随开挖扰动而发生变化,其他边界均不排水。由于问题的对称性,取计算模型的一半进行分析,约束模型底部、左右边界以及远离对称面一侧边界的所有位移。隧道衬砌部分的位移假定为零。为了提高计算效率,在开挖面附近使用更加精细的网格。

图2 隧道开挖模型及有限元网格划分Fig.2 Diagram of the shield tunnel and the used mesh
2.2 算法验证
首先对所建立的计算方法及简化模型进行验证,为了与文献中的结果进行对比,假定隧道直径为10m,隧道埋深为10m,地表孔隙水压力为零,土体的有效黏聚力和内摩擦角分别为5kPa和30°,土体天然重度为17kN·m-3,饱和重度为21kN·m-3。考虑三种计算条件,条件一为考虑渗流影响,条件二为不考虑渗流影响且采用天然重度,条件三为不考虑渗流影响且采用饱和重度。三种条件下计算得到的极限支护力如图3中水平虚直线所示,并与文献[13]结果进行了对比。从图中可以看到,本文结果与文献结果非常接近,验证了本文计算方法及计算模型的正确性。

图3 计算结果验证Fig.3 Verification of the present formulation
2.3 渗流场分析
渗透系数各向异性最直观的影响体现在开挖面周围孔隙水压力及渗透速度分布上。假定渗透系数为正交各向异性,水平方向上渗透系数相等。以下分析中所考虑的计算工况如表1所示,分别研究不同水位高度、隧道埋深和土体强度下渗透系数各向异性对开挖面稳定性的影响,参考工程经验,假定渗透系数比值在0.1~4之间变化。图4所示为C/D=2,Hw=10m时,大致均匀选取4个渗透系数比值所对应的隧道开挖引起开挖面附近孔隙水压力分布。从图中可以看出,当渗透系数比大于1时,隧道开挖对孔隙水的扰动范围在竖直方向较大,水平向较小;反之,当渗透系数比小于1时,孔隙水扰动范围在水平向较大,竖直向较小。kv/kh=0.1时,隧道上部地层孔压场几乎没有变化,而开挖面水平方向上出现较大范围低值孔压区。

图4 渗透系数各向异性条件下开挖面附近孔隙水压力分布Fig.4 Pore pressure contours considering the anisotropy of the permeability
图5 所示为开挖面竖直中心线上渗透速度分量的分布,坐标以竖直向上为正。从图中可以看出,不同工况下开挖面上渗透速度在两侧较大,中间位置较小,也比较平缓。随着渗透系数比kv/kh的减小,渗透速度各个分量均不断减小,尤其是渗透速度的竖直分量。图中给出了开挖面上渗透速度矢量的示意图,当渗透系数比较大时,孔隙水的流动倾斜向下,而当渗透系数比较小时,孔隙水则呈水平向流动。由动水力的定义可知

式中:GD为动水力;iw为水头梯度。
由达西定律可知

式中:k为渗透系数矩阵。将式(20)代入到式(19)后得

可见,动水力的大小和渗透系数规则化后的渗透速度有关,为了反映渗透系数各向异性对开挖面稳定性的影响,计算了开挖面渗透速度的绝对值以及规则化渗透速度绝对值如图6所示。随着渗透系数比kv/kh的增大,开挖面渗透速度绝对值逐渐增大,这说明开挖面附近的渗透力随着渗透系数比的增大而增大。究其原因,当渗透系数比较大时,开挖面上方的孔隙水受扰动较大,在孔压梯度的作用下流入开挖面。需要说明的是,上述结论在稳态渗流的假设下得到,在瞬态渗流条件下结果可能会有所不同。

表1 计算参数Tab.1 Parameters used for stability analysis

图5 渗透系数各向异性条件下开挖面渗透速度分布Fig.5 Seepage rate along the excavation face considering the anisotropy of the permeability

图6 开挖面渗透速度对比Fig.6 Comparison of seepage rates on the excavation face
2.4 极限支护力分析
由上述讨论可知,渗透系数各向异性对开挖面附近孔压场及动水力有较大的影响,因而,盾构隧道开挖面极限支护力也会较各向同性条件有很大不同。本节采用数值极限分析方法,对各种工况下开挖面所需极限支护力及破坏机制进行探讨。图6中所对应的四种渗透系数比条件下,开挖面速度场分布如图7所示,云图黑色区域代表了破坏时土体速度场分布绝对值的大小。可以看出,随着渗透系数比的减小,破坏区域的水平范围逐渐增大;破坏区域的竖向范围未见有明显的影响。另外,破坏面整体形状也不随渗透系数比值发生变化。

图7 渗透系数各向异性对开挖面破坏机制的影响Fig.7 Effect of permeability anisotropy on the collapse mechanism
图8 所示为埋深10m时,不同水位条件下开挖面极限支护力随渗透系数比值的变化,其中piso指的是各向同性条件下所对应的极限支护力。由图可见,开挖面极限支护力随渗透系数比值的增加而不断增加,这和上节中得到的结论是吻合的。极限支护力的增加速率随渗透系数比值的增加逐渐减小,最终趋于一个稳定值。渗透系数比小于1时,渗透系数各向异性影响较大,渗透系数比大于1时,渗透系数各向异性影响较小。因而,可以将1作为渗透系数比的影响阈值,也就是说,当竖向渗透系数小于水平向渗透系数时,渗透系数各向异性所表现出的特征才更为显著。与各向同性极限支护力的比值则不随地表水位而变化,具有完全相同的变化规律。图9所示为不同埋深条件下开挖面极限支护力的变化,从图中可以看出,随着埋深的减小,开挖面极限支护力逐渐增大,极限支护力随渗透系数比的变化规律则是相似的。从规则化后的极限支护力变化规律可以发现,渗透系数各向异性的影响随着埋深的增加而增大,这主要是由于当埋深较大时,各向异性的岩土体区域随之增大。埋深和水位均为10m时,不同内摩擦角条件下,渗透系数各向异性对开挖面极限支护力的影响如图10所示。从图中可以看到,不同内摩擦角条件下极限支护力的变化规律相似,渗透系数比的影响随着摩擦系数的增加而增大。原因在于极限支护力随着内摩擦角的增大而迅速减小,当内摩擦角较大时,极限支护力中的渗透力部分较大,从而导致渗透系数各向异性的影响更加明显。同时,从图8~图10中可以发现,不同工况下,渗透系数比的影响阈值变化不大。
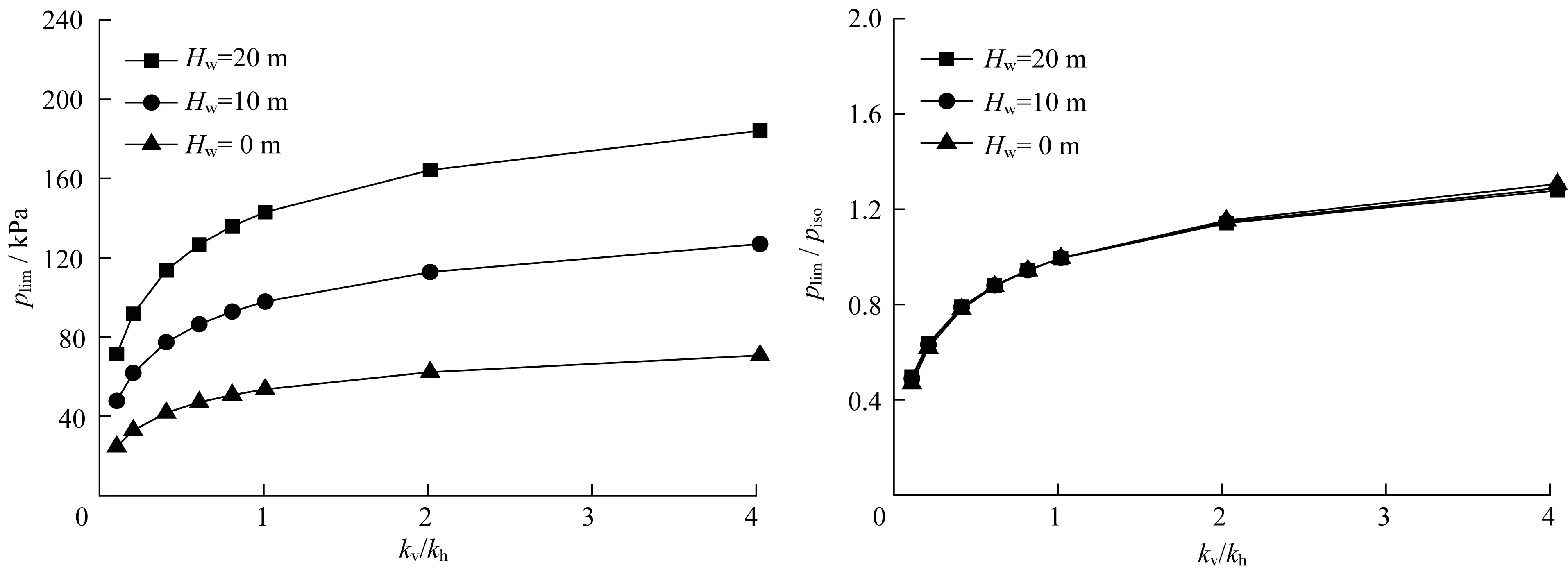
图8 不同水位条件下渗透系数各向异性对开挖面极限支护力的影响Fig.8 Effect of permeability anisotropy on limit supporting pressure for different water levels

图9 不同埋深条件下渗透系数各向异性对开挖面极限支护力的影响Fig.9 Effect of permeability anisotropy on limit supporting pressure for different buried depths

图10 不同内摩擦角条件下渗透系数各向异性对开挖面极限支护力的影响Fig.10 Effect of permeability anisotropy on limit supporting pressure with respect to different friction angles
3 结论
本文基于极限分析理论,结合有限元四面体单元和半正定锥规划,建立了三维数值极限分析方法。在此基础上,结合渗流分析,研究渗透系数各向异性条件下盾构隧道开挖面附近渗流场及开挖面极限支护力的变化规律,分析渗透系数比对开挖面破坏模式的影响,为盾构隧道安全施工提供重要的参考。主要结论如下:
(1)随着竖向与水平向渗透系数比的增大,开挖面渗透速度绝对值逐渐增大,这说明开挖面附近的渗透力随着渗透系数比的增大而增大。原因在于,当竖直向渗透系数较大时,开挖面上方的孔隙水受扰动较大,在孔压梯度的作用下流入开挖面。
(2)随着竖向与水平向渗透系数比的减小,开挖面破坏区域的水平范围逐渐增大,破坏区域的竖向范围未见有明显影响。破坏面形状不随渗透系数比值发生变化。
(3)不同工况下,开挖面极限支护力随着竖向与水平向渗透系数比增加不断增大,增加速率逐渐减小,极限支护力最终趋于一个稳定值。渗透系数比值对极限支护力的影响随着隧道埋深和内摩擦角的增加而增大,不受地表水位的影响。
