含水合物地层井壁力学状态的弹塑性解析分析

2021-01-08王华宁郭振宇蒋明镜

同济大学学报（自然科学版） 2020年12期

王华宁，郭振宇，高翔，蒋明镜

（1.同济大学航空航天与力学学院，上海200092；2.同济大学土木工程防灾国家重点实验室，上海200092；3.天津大学建筑工程学院，天津300350）

天然气水合物是一种分布范围广、储量丰富的新型清洁能源，目前发现的天然气水合物超过90%存在于海底沉积物中［1］。包括中国在内的多个国家已提出水合物开采计划并进行了开采试验。由于钻井和开采过程中环境和边界条件改变造成的水合物分解和井周土体力学性能劣化，在多国试采中均出现过生产井周土层的垮塌失稳等事故［2-3］。井壁垮塌、破裂、缩径等现象称为井壁失稳，是水合物开采所面临的主要问题之一［2-4］。水合物分解造成土体力学特性劣化是影响井壁稳定的关键因素，该过程涉及温度场、渗流场等多个物理场与力场的相互作用。目前，针对水合物地层井壁稳定问题的研究多采用数值模拟的方法。Li等［5］利用数值方法研究了水合物储层的深度、分解范围和分解后的力学性能对井壁纵向沉降的影响。宁伏龙等［6］考虑了钻井液特性对其侵入地层的影响，通过一维数值模型研究过压钻井条件下的井壁安全问题。Sun等［7］建立了数值模型研究钻井液特性、储层的渗透率及饱和度对井壁力学状态的影响，并基于Mohr-Coulomb（MC）准则考虑了地层的屈服。相比之下，将关键因素抽象简化后得到的解析解答能够高效地进行参数分析，并可分析参数在解答中的作用，进行力学机理的探究。本文将建立解析模型，研究深海含水合物地层中井壁稳定问题。

传统井壁、隧道/巷道力学分析的解析研究多针对弹/黏弹性［8-9］、弹塑性问题展开［10-16］。目前针对弹塑性模型的研究，一般考虑各向等压圆形孔洞的受力问题（轴对称问题）［10］。弹塑性问题的解答通常基于 M-C［11］、Hoek-Brown［12］屈服准则和统一强度理论［13］等，以及理想塑［14］、弹脆塑［15］和考虑非线性软化［16］等本构关系得到力场的解析或半解析解答。上述研究主要针对孔洞周边为单一岩土材料，部分解答中考虑渗流场对力场的影响。水合物井壁稳定问题的特殊性和复杂性主要在于①由于水合物对环境温度和压力的改变非常敏感，在钻井过程中水合物可能发生分解，而分解造成微观结构的变化（例如孔隙率变大）也影响温压分布；②水合物分解对土体力学特性影响显著，导致井壁承载能力下降，必须在计算物理场和力场时区分对待分解和未分解域；③温度和渗流场对力场存在多种影响。在冻结法施工［17］中冻结壁分析、支护隧道分析［18］［19］等属于多域问题，但并未涉及温度和渗流的共同作用，或是基于弹性本构的计算，且结构本身的尺度和特性与水合物地层中井壁问题有很大区别。Wang等［20］考虑上述多场关系，建立了水合物地层井壁稳定的弹性模型，并通过屈服准则进行井壁稳定的初步分析。

本文对实际问题进行合理简化，考虑水合物分解对地层渗透、导热和力学特性的影响，以及渗流场对力场的作用，基于M-C准则和理想弹塑性模型，推导了水合物地层中井周应力和位移的弹塑性解答，并利用解析模型对井壁的稳定性进行分析。

1 力学模型

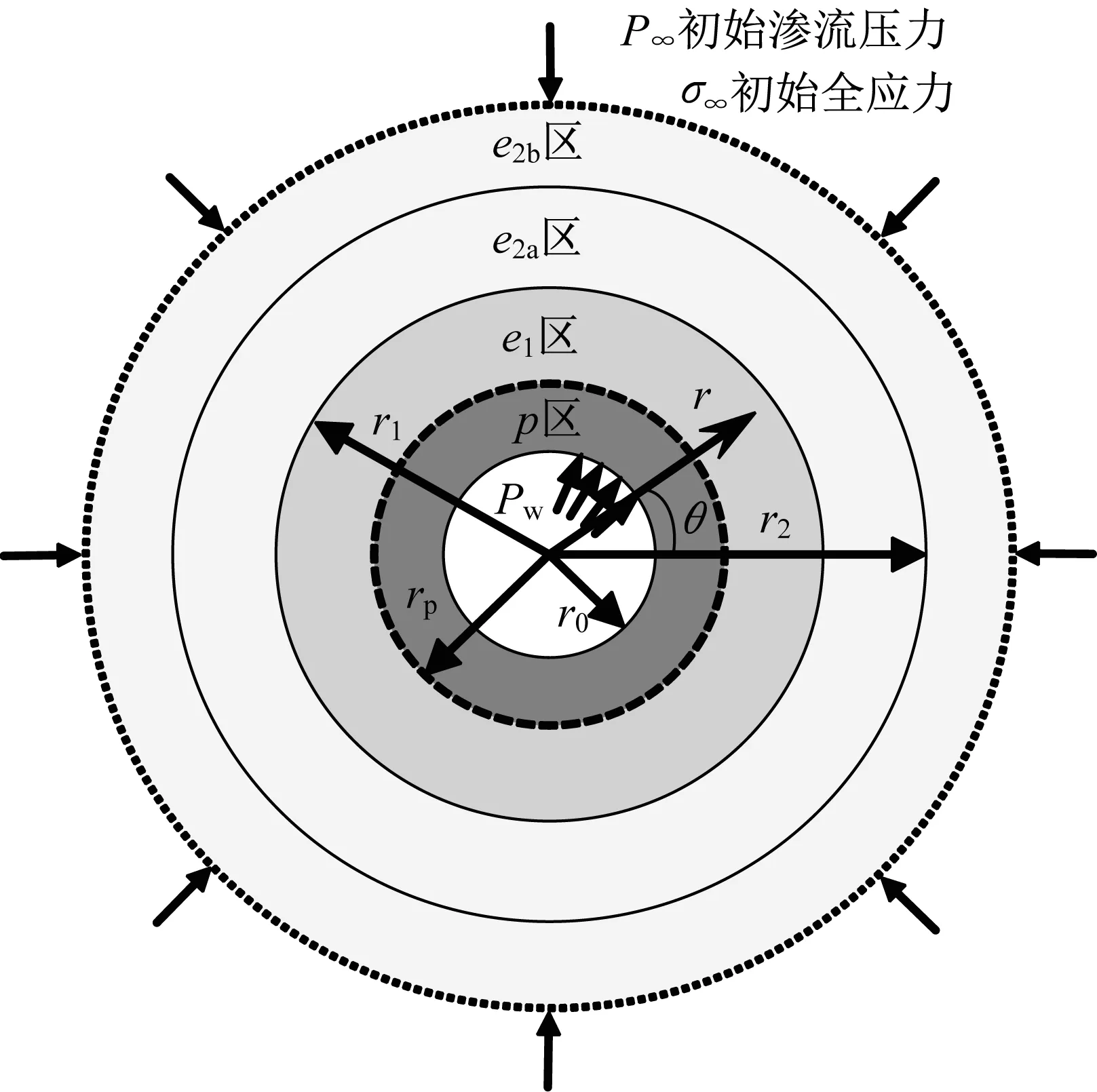
图1 水合物地层中井壁稳定力学模型Fig.1 Mechanicalmodelforwellboredrillingin methane hydrate-bearing sediments

本文主要研究含水合物地层钻井过程中，在井口横截面内由于过大的应力/位移而导致的井壁失稳问题，未涉及井壁纵向失稳和开采过程中出砂淤堵等其他失稳方式。由于井轴向尺寸远大于井口半径，且储层所处地应力较大，可忽略竖向重力梯度影响，因此简化为水平截面内平面应变问题。有研究显示，面内两方向初始应力可认为近似相等［21］；上下有不透水层，假定温度和渗流场也仅与径向位置相关，为轴对称问题。与传统问题不同的是，钻井引起的井周温度和渗流压力的改变导致一定区域内水合物分解，从而引起分解域土体参数改变，因此水合物井壁为多域问题。本文关注时间较大时刻的稳态问题，此时对应的力场最危险。根据以上简化，几何模型和受力情况见图1，由内到外依次为：p区（r0≤r≤rp）：分解域塑性区；e1区（rp＜r≤r1）：分解域弹性区；e2a区（r1＜r≤r2）：未分解域弹性区（有温压变化）；e2b区（r＞r2）：无穷域（温压保持原始值）。在p区和e1区将考虑水合物分解对热量和压力传递参量以及力学参数（弹性模量和黏聚力）的影响。根据试采和数值分析结果［6］发现钻井引发的温度和压力的改变仅在井壁有限范围内，因此设置e2a区，其中r2为温压影响的最大半径。而最外侧的e2b区内的温度和压力未受到钻井影响，均为原始值。图中Pw为钻井液压力，总应力σ∞作用在无穷远处。推导中多场相互影响关系见图2。考虑渗流压力对储层有效应力的影响，未考虑应力场对渗流场和温度场的影响；地层假定为满足M-C准则的理想弹塑性模型。由于钻井过程分解域较小，为简化求解，忽略分解域和未分解域之间过渡区域的影响，并且仅考虑塑性区在分解域内的最常见情况（rp＜r1）。

2 温度场/渗流压力场解答

图2 力场、渗流场和温度场的耦合关系Fig.2 Coupling relationship between mechanics,seepage and temperature field

钻井引发井周温度和孔隙压力变化，导致一定范围内水合物发生分解，并使地层导热和渗透系数变化，引起渗流场和力场的进一步改变。由于该阶段分解域较小，且考虑时间足够长的稳态问题，因此忽略水合物分解产生的水气及热量变化的影响。本节给出温度场和渗流压力场的解析表达式，并确定分解域范围。

2.1 温度场

根据假定，本问题为稳态轴对称温度分布。考虑热传导的热量传递方式，存在的热对流形式通过增大分解域内的导热系数近似考虑［22］。稳态热传导问题的控制方程和定解条件为（轴对称）：

式中，Tw表示钻井液温度，T∞表示储层初始温度，λ1和λ2分别表示分解域和未分解域的热传导系数。无穷域内（r≥r2）温度保持在初始值。求解式（1）得到含有待定系数的通解，得

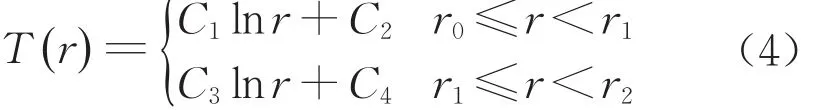
将式（4）代入式（2）～式（3）中可确定待定系数C1～C4，最终得到温度场

2.2 渗流压力场

认为孔隙中流体流动满足达西定律，稳态渗流场的控制方程和定解条件为

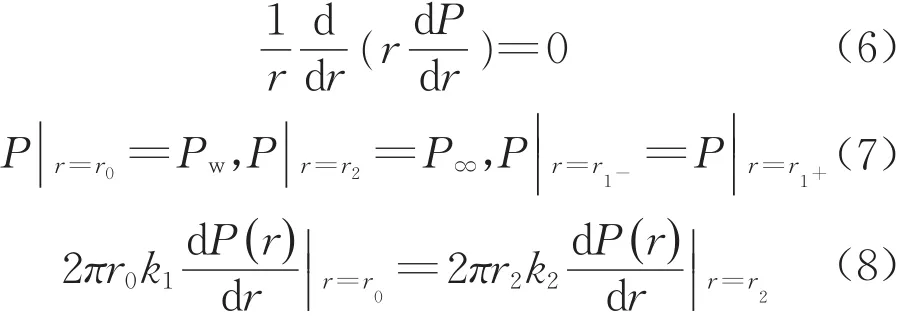
式中，k1和k2分别表示分解域和未分解域的渗透系数。与温度场的数学求解过程相似，由式（6）～（8）可确定孔隙压力分布规律为

与未考虑分解域的单域问题不同，上式中温度/压力场均与分解域的相对热传导系数（λ1/λ2）和相对渗透系数（k1/k2）相关。

2.3 分解域的确定

水合物的相平衡方程可通过海水中纯水合物的相平衡试验数据［23］拟合得

式中：P的单位为kPa；T的单位为oC。在r=r1处温度与压力应恰好满足上述关系，在分解域内，实际渗流压力小于上式的计算值。将T(r1)和P(r1)代入式（10）可求解分解域半径r1。

3 应力和位移场解答

当钻井液压力在一定范围内时，井壁全域处于弹性阶段，当钻压过小或者过大时，井壁将进入塑性［20］。本节将推导弹性阶段和塑性阶段应力及位移场的解析表达式。规定压应力为正，位移朝向井眼为正。

3.1 力学模型与基本方程

试验结果显示，在较高的围压下含水合物土体进入塑性阶段后，没有出现明显的应变软化或硬化［24］，因此本文采用理想弹塑性模型模拟水合物地层。井壁附近水合物的分解引起分解域弹性模量和黏聚力发生变化，即

式中：E1和c1表示分解域的弹性模量和黏聚力；E2和c2表示水合物地层的原始弹性模量和黏聚力，均为常数。水合物分解对储层泊松比（ν）和内摩擦角（φ）影响很小，可以忽略［25］。

极坐标系下的平衡方程为

式中：σri和σθi表示径向和环向正应力（有效应力），α为有效应力系数。几何方程为

式中：εri和 εθi表示径向和环向应变；ui表示径向位移。上标i=p，e1，e2a，e2b分别表示塑性区以及三个弹性区中的变量。

弹性区有效应力与应变关系满足胡克定律：

式中：i=e1，e2a，e2b，弹性模量满足认为地层满足Mohr-Coulomb屈服准则，用主应力表示的屈服准则为

塑性应变满足非关联的流动法则为

式中：εrpa和εθpa表示塑性区的径向和环向塑性应变，当径向应力为第一主应力时，β=(1-sinψ)/(1+sinψ)，当环向应力为第一主应力时，β=(1+sinψ)/(1-sinψ)，ψ表示剪胀角。

以上是本文解析模型涉及的基本方程。此外，模型需要满足边界条件和连续性条件。井壁和无穷远处的边界条件（有效应力）为

对于弹性问题j=e1，对于弹塑性问题j=p。相邻区域在交界面处的应力和位移协调条件包括：

井壁稳定问题关注的是全部有效应力（初始应力和钻井引发的增量应力之和）和钻井引起的增量位移。图3a为增量问题的计算模型，可通过图3b给出的全量模型减去图3c模型得到。其中σef1=σ∞-αP∞为无穷远处初始有效应力；σef2=Pw(1-α)为井周钻井液压力提供的有效应力。根据上述模型的关系，应力有如下叠加关系，即

式中：i=p，e1，e2a，e2b。和表示增量应力（图3a）；σri和 σθi表示全量应力（图3b）；σr0i和σθ0i表示图3c所示弹性模型的应力。三个模型弹性区的应力和位移都各自满足式（12）～式（15）的基本方程，图3b塑性区有效应力满足屈服准则。

3.2 弹性阶段应力/位移

首先求解图3c所示模型的应力与位移。由于钻井前地层孔隙压力为常数（P∞），e2a和e2b区可以合并为一个e2区。此时全域处于弹性阶段，将式（13）代入式（14）～（15），得到应力与位移的关系式，再将应力表达式代入式（12）得到关于位移的微分方程为

图3 应力与增量位移计算Fig.3 Models for stress and incremental displacement calculation

此时dP(r)/dr=0，求解该微分方程可得到i区（i=e1，e2）的位移表达式，再代回到式（14）～式（15），可得到相应的应力表达式，结果如下所示：

下面求解弹性阶段井壁的全量应力及增量位移，共有三个分区（e1、e2a、e2b）。与推导式（26）～式（28）的过程相似，通过联立式（12）～式（15），可得各分区位移的微分方程，求解后得到含有待定系数的表达式。

当i=e1，e2a时，dP(r)/dr≠0，应力及位移表达式为

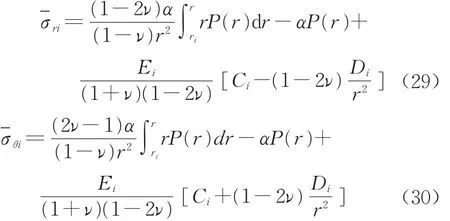
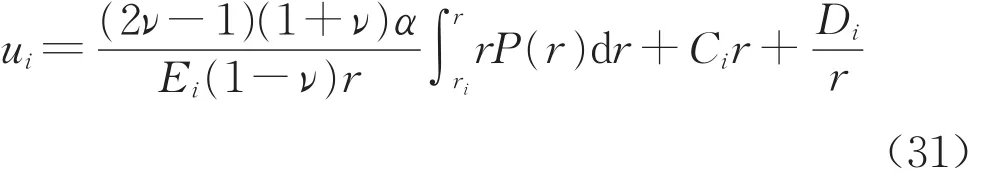
式中：Ci，Di为待定系数，积分下限re1=rp，re2a=r1。

无穷域（i=e2b）内的孔压为常数，因此应力和位移的表达式在形式上与式（26）～式（28）相同，即

对于弹性问题，将已求解待定系数的表达式（26）和还未求解含有待定系数的表达式（29）、（32）代入式（23）得到径向全应力σri，再将σri与增量位移表达式（31）、（34）代入弹性问题的定解条件（18）、（19）、（21）、（22），求解待定系数Ci，Di（i=e1，e2a，e2b），可得到弹性问题应力和位移的解析表达式。限于篇幅，文中未列参数具体表达式。

3.3 弹塑性阶段应力/位移

平面应变条件下，塑性区的轴向应力σz为中间主应力［26］，而径、环向应力的大小关系可通过井壁弹性解答中井口处的径向应力和环向应力大小进行判断。确定主应力顺序后，联立式（12）和式（16），并将渗流场表达式（9）代入，求解关于塑性区应力的微分方程，得到塑性区主应力的表达式。当环向应力为第一主应力时，微分方程为

求得塑性区应力表达式为

当径向应力为第一主应力时，微分方程为

求得塑性区应力表达式为

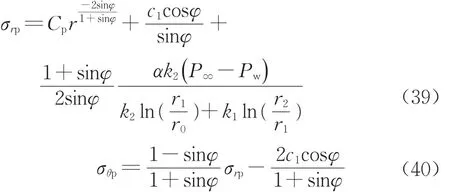
式中：Cp为待定系数，通过式（18）的边界条件确定。可以看出塑性区应力与塑性区半径没有直接关联。

下面求解增量位移。认为塑性区的总应变为塑性应变和弹性应变之和，可表示为

式中：εrpb和εθpb为塑性区的径向和环向弹性应变。联立式（17）和式（41）可得εrp+βεθp=εrpb+βεθpb，将式（13）代入该式左端后得到塑性区位移需满足的微分方程如下：

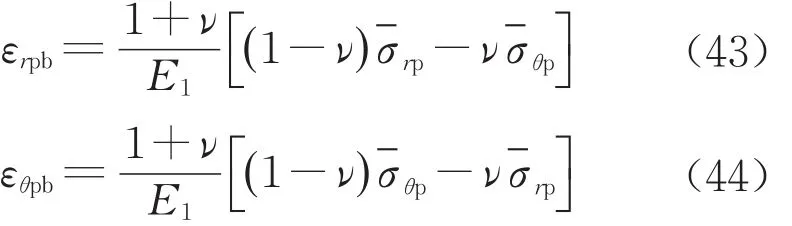
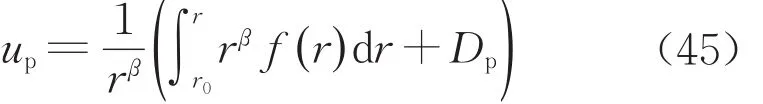
式中：Dp为待定系数。

在弹塑性阶段，三个弹性区的应力和位移的控制方程与4.2节一致，将已求解待定系数的塑性区应力表达式（36）、（37）（或（39）、（40））和含待定系数的弹性区应力、位移表达式（29）～式（32）、（34），塑性区位移表达式（45）代入定解条件式（19）～式（22），得到关于待定系数Dp以及Ci、Di（i=e1，e2a，e2b）和塑性区半径rp的方程组，待定系数可直接求解或写成关于rp的表达式，最终可得到关于rp的超越方程，用数值方法求解rp后可确定各个待定系数的值，得到弹塑性问题的应力及位移解答。限于篇幅，此处未给出具体方程和结果。

3.4 模型验证

为了验证推导过程的正确性和模型的适用性，本节将数值模型的结果与本文解答进行比对。

利用ABAQUS软件建立同等假设下的有限元模型进行比对验证，如图4所示。有限元模型选择轴对称的建模方式，分区从内到外依次为分解域、未分解域和无穷域。分解域大小需根据3.3节计算得到。首先给模型施加初始地应力和渗流压力，并进行地应力平衡，第二步改变r=r0处的应力和渗场边界条件，得到最终的应力和位移分布。参数设置如下：孔径r0=0.2m，未分解域半径r2=3m，弹性模量E1=40MPa，E2=100MPa，泊松比ν=0.3，黏聚力c1=0.5MPa，c2=2MPa，内摩擦角φ=23°，剪胀角 ψ=0°，渗透系数 k1/k2=4，热传导系数λ1/λ2=4，无穷远处的应力、渗流压力和温度分别为σ∞=15.6MPa，P∞=12MPa，T∞=8°C，有效应力系数α=0.7。分解域半径r1按第3节的推导过程计算，另取r3=150r0作为有限元模型的外边界。在本文分析的参数范围内，计算发现欠压条件下环向应力为第一主应力，过压条件下径向应力为第一主应力。图5a、图5b分别给出欠压模型（Pw=8MPa，Tw=18°C，r1=8.2r0）和过压模型（Pw=21MPa，Tw=23°C，r1=4r0）的比对情况。在r=r1处由于分解域弹模劣化引起环向应力突变。结果表明解析解与有限元模型的应力、位移曲线及塑性区半径均吻合较好。

图4 轴对称有限元模型Fig.4 Axisymmetric model in finite element method

图5 解析解与有限元结果比对Fig.5 Comparison between analytical solution and finite element results

由于目前缺乏含水合物地层井壁稳定的实验和工程测量数据，本文通过与数值模型进行比对，验证解析解答的适用性。图6为本文应力解答与文献［6］中基于复杂数值模型力场部分的结果比对。该数值模型基于南海神狐海域含水合物地区的测井数据，考虑了气液两相流，以及水合物分解和二次生成引起的热量变化，求解了非稳态的渗流、温度等物理场影响下的地层应力。选取t=24h的时刻，结果表明本文提出的解析解与数值解的径向应力吻合较好，解析解的环向应力在近井壁处的塑性区内（A、B点）与数值解误差较小，在距离井壁较远的弹性区内（C点）略低于数值解，总体上应力沿径向的变化趋势与数值解一致，且塑性区半径的结果相近。

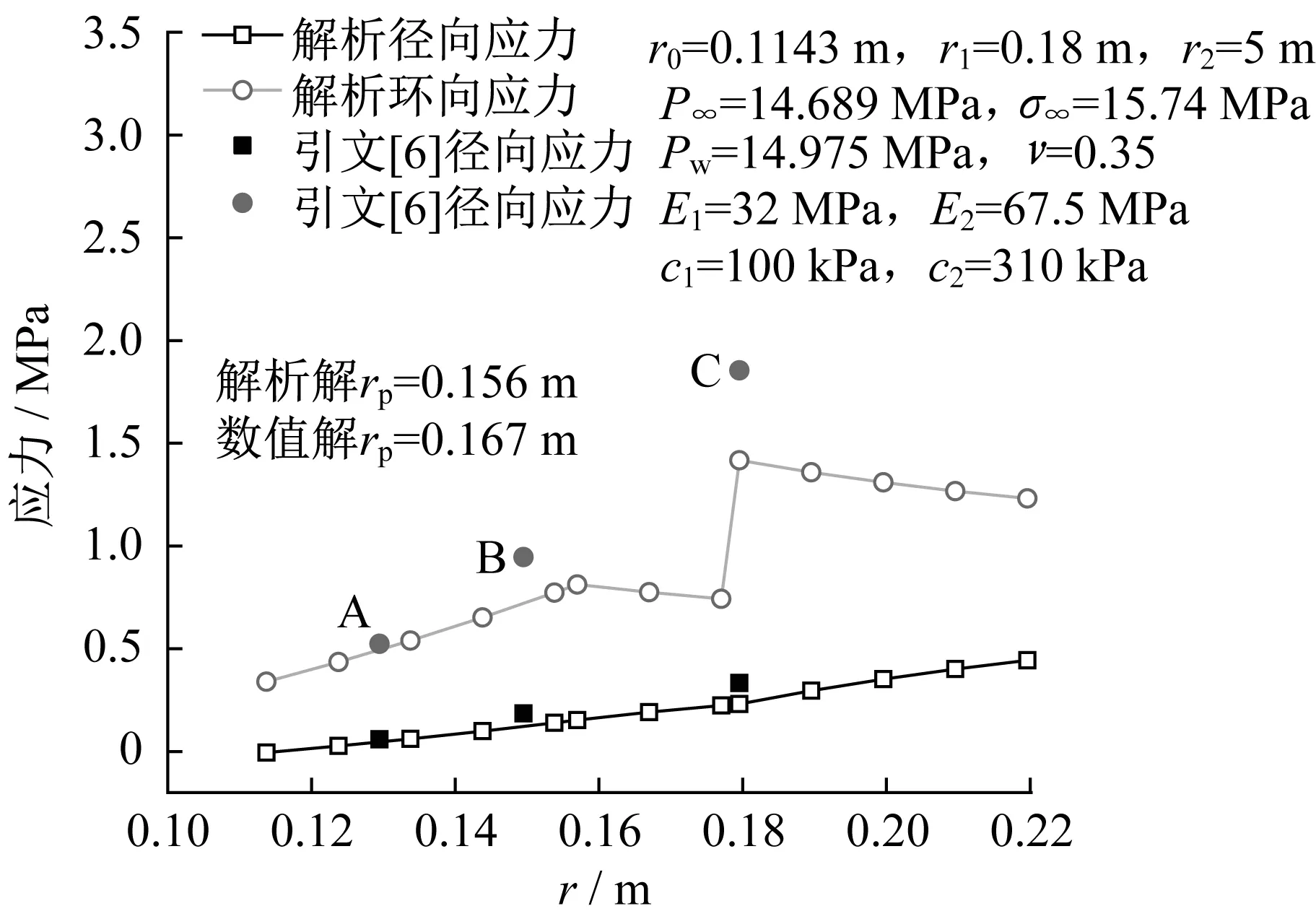
图6 解析解与复杂模型数值结果比对Fig.6 Comparison between analytical solution and numerical solution under complex conditions

4 参数分析

储层进入塑性或发生较大的位移会增大井壁失稳的风险，本文将用塑性区的大小和储层的径向位移反映井壁的稳定性。本节利用解析模型分析钻井液压力Pw、分解域大小r1、弹性模量劣化程度E1/E2以及黏聚力劣化程度c1/c2等因素对含水合物地层井壁稳定性的影响。取E2=100MPa，c2=2MPa，φ=18°，其它参数与4.4节相同。位移均采用量纲为一形式u/u0，其中u0=σ∞r0/2G2为无渗流、无钻井液压力、无水合物分解情况下井壁处位移，G2=E2/(1+2ν)为未分解域的剪切模量。

4.1 钻井液压力对力场的影响

钻井液压力对保持井壁稳定非常重要，过大或过小均会引起井壁失稳。为仅凸显钻井液压力的影响，通过调节温度Tw使分解域半径均为r1=4r0。图7～图8分别给出欠压和过压钻井情况不同钻井液压力下位移和应力随位置的变化。不同情况的Pw和Tw已在图中给出。可以看出钻井液压力对径向应力影响较小，对环向应力的影响较为明显。由位移变化可知，欠压钻井时，井眼附近塑性变形较为严重，随着与井壁距离的增大位移逐渐减小；当钻井液压力增大时，井壁的径向位移和塑性区半径逐渐减小。过压钻井时，由于井壁附近孔隙压力较高，水合物不易分解，井壁不易进入塑性。只有当钻井液温度和压力值非常高时才会出现明显的分解域和塑性区。由图8b可知，过压条件下最大径向位移不一定出现在井壁边缘（r=r0），当钻井液压力较小时可能出现在未分解域（r1＜r≤r2）中，且塑性区位移相比于欠压钻井时更小；塑性区位移对钻压的变化较为敏感，随着钻井液压力增大，井壁的径向位移和塑性区半径逐渐增大。

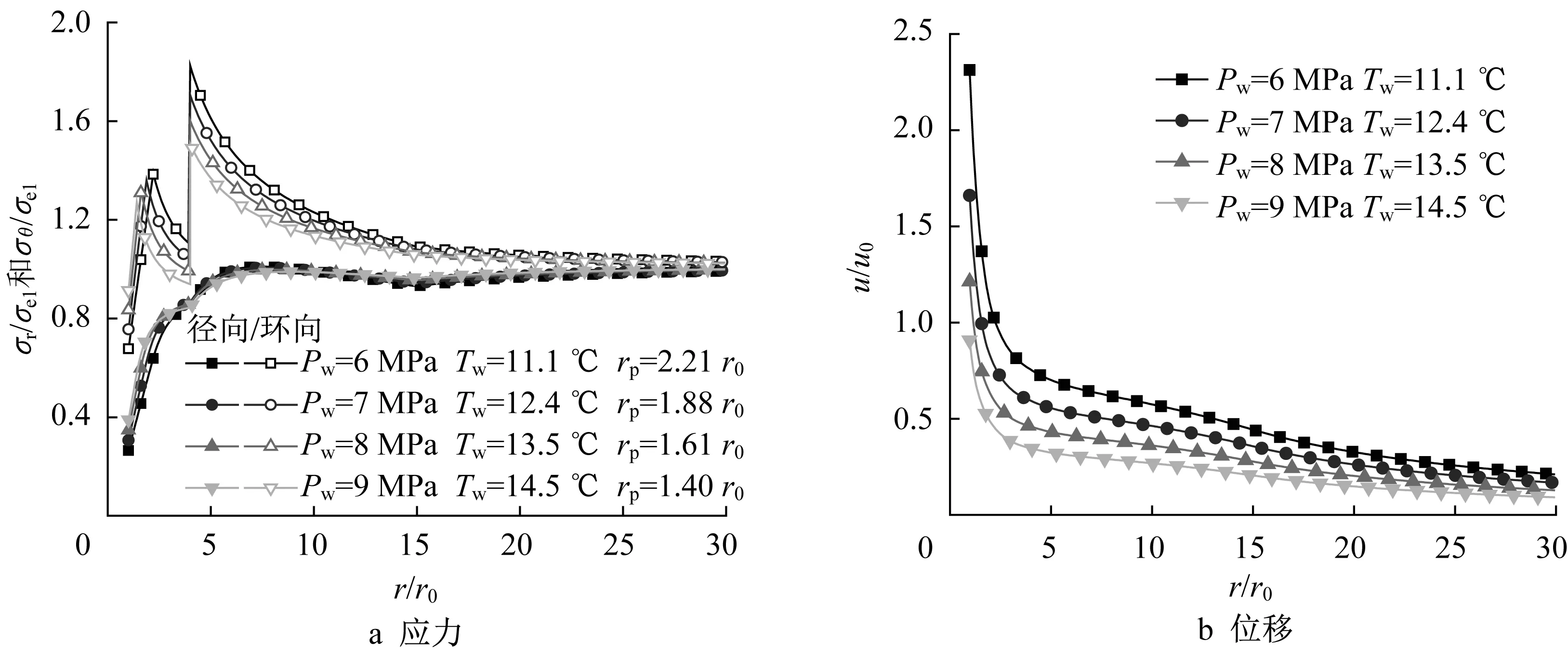
图7 欠压钻井时钻井液压力对应力和位移的影响Fig.7 Influence of drilling fluid pressure on stress and displacement under underbalanced drilling condition

图8 过压钻井时钻井液压力对应力和位移的影响Fig.8 Influence of drilling fluid pressure on stress and displacement under overbalanced drilling condition

4.2 分解域半径对塑性区范围的影响

当分解域变大时，塑性区变大的程度是水合物地层钻井时关注的重要问题。保持钻井液压力不变，通过调节Tw改变分解域范围，图9给出欠压和过压钻井下塑性半径（rp）随分解域半径的变化，其中分解域的黏聚力和弹性模量分别为c1=0.25c2，E1=0.5E2。当r1/r0=1时表示水合物未分解，由图可见，随着分解域范围的扩大，塑性区先是急剧增大，然后增大趋势逐渐变缓，且始终没有超出分解域，与本文的假设一致。对比两组数据可以发现，随着分解域的扩大，过压钻井模型的塑性区比欠压钻井模型增长更快。

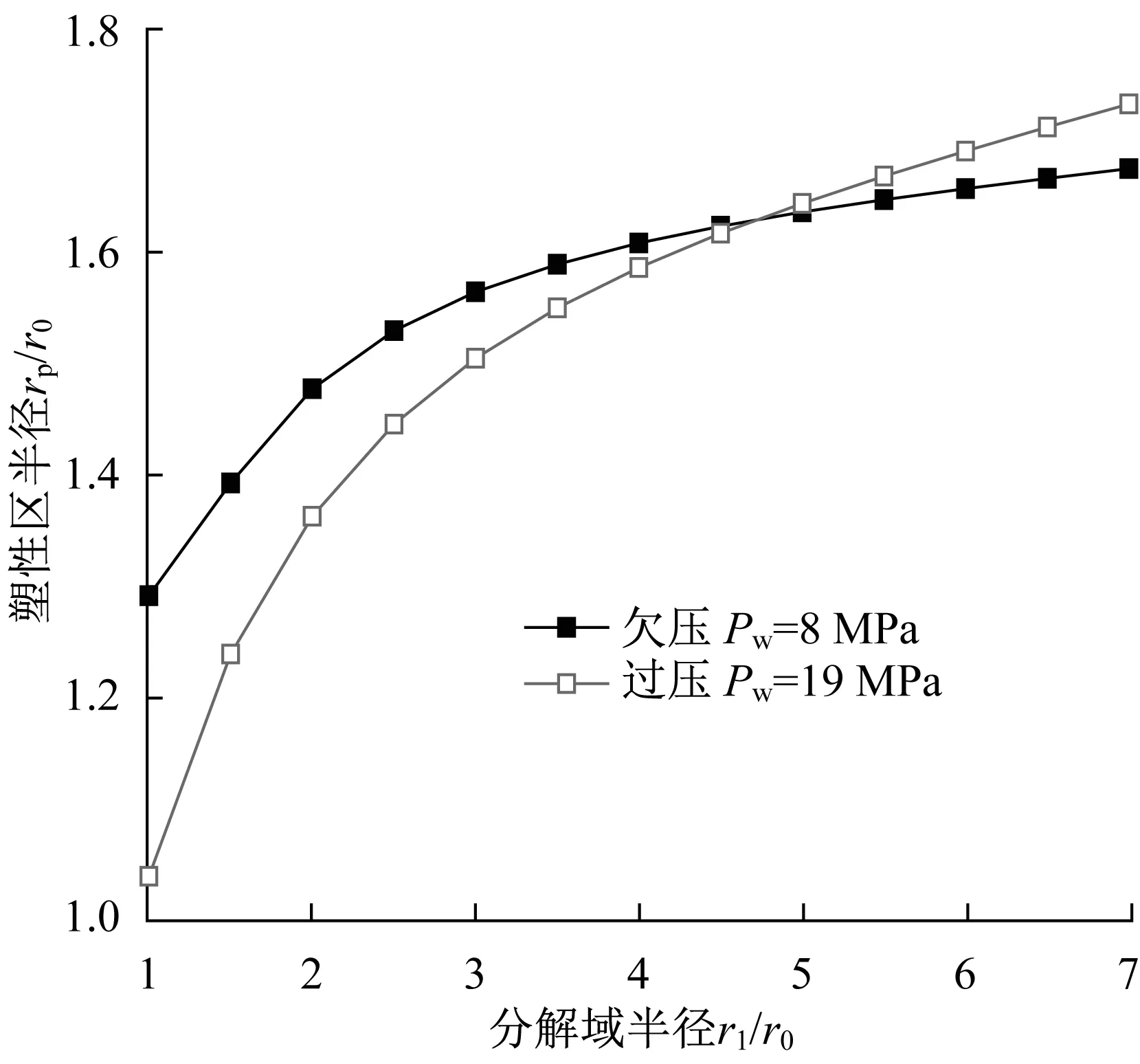
图9 分解域大小对塑性区半径的影响Fig.9 Influence of the size of dissociation region on the radius of plastic zone

4.3 弹性模量/黏聚力劣化程度对力场的影响

图10 欠压钻井时弹性模量劣化程度对应力和位移的影响Fig.10 Influence of the reduction of elastic modulus on stress and displacement under underbalanced drilling condition

图11 过压钻井时弹性模量劣化程度对应力和位移的影响Fig.11 Influence of the reduction of elastic modulus on stress and displacement under overbalanced drilling condition

考虑到实际情况由于水合物分解所引起的弹模劣化程度有限，仅在一定范围内对参数进行讨论。保持分解域半径一致（r1=4.7r0），取c1=0.25c2，图10～图11给出欠压和过压钻井时不同弹模劣化程度下的应力和位移分布。可见弹模变化对塑性区应力值无影响，但对塑性区大小有影响。欠压钻井时，随着弹性模量劣化程度的提高，塑性区逐渐减小；过压钻井时，随着劣化程度的提高塑性区逐渐增大。两种情况下，随着弹模劣化程度提高，径向应力在全域内逐渐减小，而环向应力在分解域内逐渐减小，在未分解域内逐渐增大。位移方面，随着弹模劣化程度的提高，地层的径向位移有小幅增长，对欠压情况的影响更为明显。黏聚力劣化程度对塑性区的影响如图12所示，保持分解域半径一致（r1=4.7r0），取E1=0.5E2。可以看出，欠压和过压钻井下分解域内黏聚力劣化越严重，塑性区半径rp越大，且呈现近似线性的关系。水合物有多种赋存类型，其中胶结型水合物的分解对储层的黏聚力影响最大，因此分解引起的塑性区增长相比于其它类型的水合物储层将更为显著。