混合梁刚构桥受力计算方法与合理结构体系研究

2021-01-08曾明根许桂修林志平陈德宝苏庆田

同济大学学报（自然科学版） 2020年12期

曾明根，许桂修，林志平，陈德宝，苏庆田

（1.同济大学土木工程学院，上海200092；2.福建省高速公路集团有限公司，福建福州350001）

随着交通事业快速发展，我国建成了大量预应力混凝土连续刚构桥，但是当其跨径超过200m时，混凝土主梁的自重将严重限制其跨越能力的继续发展，且以跨中梁体开裂与过大下挠为典型代表的耐久性问题也成为其一大弊病［1-2］。为此，有学者提出在混凝土刚构桥的主跨中部位置上用部分钢梁来代替混凝土梁，从而形成钢--混凝土混合梁刚构桥，能很好地解决传统混凝土刚构桥在主跨跨中由于混凝土材料带来的问题，同时也避免了采用全钢主梁所产生的高昂造价［3］。此外相比混凝土连续刚构桥，钢-混凝土混合梁刚构桥的受力性能更加优异。主跨跨中部分使用钢梁使结构自重降低，边跨混凝土梁则提供了压重的作用，相比混凝土刚构桥，混合梁刚构桥的控制截面弯矩大幅降低［4］。选取一座跨径布置为84m+200m+84m的预应力混凝土连续刚构桥，自重作用下，不考虑预应力时混凝土刚构桥墩顶负弯矩 Md1为 1.9×106kN·m，跨中正弯矩 M1为1.9×105kN·m；而若在跨中选用80m的钢梁代替混凝土梁，则墩顶负弯矩Md2为1.1×106kN·m，跨中正弯矩M2为1.3×104kN·m，分别减少了43.9%与93.2%。因此钢--混凝土混合梁刚构桥不仅缓解了混凝土刚构桥长期性能问题，也实现了梁桥在跨度上的突破。

混合梁刚构桥是一种具有显着竞争力的新桥型，但目前国内外关于混合梁刚构桥的工程建设经验相对较少，建成的工程有重庆石板坡长江大桥复线桥、温州瓯江大桥、中山小榄水道大桥、舟山鱼山大桥等。邓文中等讨论了重庆石板坡长江大桥复线桥总体设计中采取的结构形式、钢-混结合段位置、预应力钢束布置情况、桥墩类型等［5］。依托于瓯江大桥，左智君建立了混合梁刚构桥中钢箱梁为等截面的数值解析模型，进行了关于内力分布和跨中挠度两个方向的优化评价［6］；谢燕梅优化了混合梁刚构桥的梁底抛物线曲线、钢箱梁与主跨长度比例、高跨比及体外束线形等［7］；苏庆田等研究了跨中钢箱梁整体提升安装的施工技术［8］。李磊等在鱼山大桥设计中探究了适用于预制悬臂拼装工艺的钢-混结合部构造设计及正交异性钢桥面板与桥面铺装的耐久性［9］。陈群等介绍了中山小榄水道混合梁刚构桥的建设条件、分跨布置、结构形式以及结合段等关键构造的设计思路［10］。此外，贺君等针对混合梁的钢-混结合段所用的PBL连接件进行了试验和理论研究［11］。

以上研究主要以中跨钢梁为等截面的混合梁刚构桥为对象，分析混合梁连续刚构桥在成桥及运营阶段的力学性能，而对于全桥采用变截面的混合梁刚构桥没有涉及到，同时对施工阶段的受力分析也鲜有考虑，但变截面钢梁的力学性能更符合混合梁刚构桥的受力需求。此外，以往的研究多借助于有限元方法开展，对于在桥梁初步设计阶段有限元方法显得有些繁琐，通过公式进行参数拟定更为方便快捷。基于此，本文依托福建泉州安海湾大桥这一中跨整体均为变截面梁的混合梁刚构桥，开展了此类桥受力计算方法与合理结构体系研究。

1 工程概述

安海湾大桥上部结构为三跨混合梁刚构桥，总体布置如图1所示，跨径布置为135m+300m+135m，总长570m。跨中钢箱梁吊装段长度为103m，钢箱梁两端通过5m长的钢混结合段与混凝土箱梁连接，目前是世界第二大跨度的混合梁刚构桥。主梁按双幅布置，全宽33.5m，上、下行分幅布置。主梁高度4.5m～15m，其中钢箱梁梁高范围4.535m～5.869m。墩顶梁高15m，高跨比为1：20，跨中梁高4.5m，高跨比为1：66.152。混凝土主梁、钢混结合段及钢主梁三部分梁高均按2次抛物线规律变化。主墩采用双薄壁等截面墩，墩高22.89m。

图1 安海湾大桥总体布置（单位：m）Fig.1 General layout of Anhaiwan Bridge(Unit:m)

2 受力性能计算方法

2.1 基本假定

为了简化理论模型，做如下假定：①结构仅受自重作用，自重集度变化规律与梁高变化规律相同；②主梁截面惯性矩可以使用近似函数模拟；③钢箱梁顶、底板及腹板厚度不变，仅考虑梁高变化；④施工过程简化为4个阶段：第1阶段为浇筑主墩；第2阶段为对称平衡悬臂浇筑混凝土箱梁；第3阶段为现浇边跨其余混凝土箱梁并合龙边跨；第4阶段为吊装钢箱梁、实现中跨合龙。

2.2 简化模型

结构简化计算模型如图2所示，图中L0为主跨跨径；L1为边跨跨径；L2为边跨现浇段长度；Lc为悬臂浇筑的混凝土梁长度；Ls为钢梁长度；H为主墩高度；EcIc为混凝土主梁抗弯惯性矩；EsIs为钢梁抗弯惯性矩；EdId为主墩抗弯惯性矩；α为混合梁梁底抛物线变化次数；A截面为边支点截面；B截面为边跨合龙处截面；C截面为墩顶截面；D截面为钢-混结合面；E截面为跨中截面；F截面为墩底截面；q1，q2，q3，q4和q5分别为A截面，B截面，C截面，D截面（钢梁）和E截面的梁自重荷载集度；xc，xs和x1分别以C截面，E截面和B截面为起点。

图2 简化模型Fig.2 Simplified model

在混合梁刚构桥的边跨与中跨的长度之比（λ=L1/L0）和主跨钢梁长度与中跨长度比（μ=Ls/L0）是影响其受力性能的两个重要因素。

由于混合梁梁高呈α次变化，基于基本假定可知边跨现浇段混凝土梁自重荷载分布为

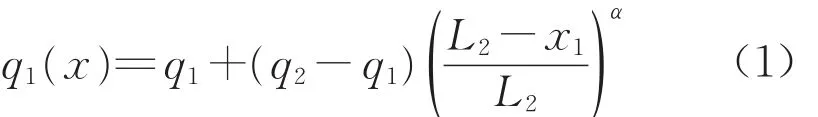
悬臂浇筑的混凝土梁段自重荷载分布为

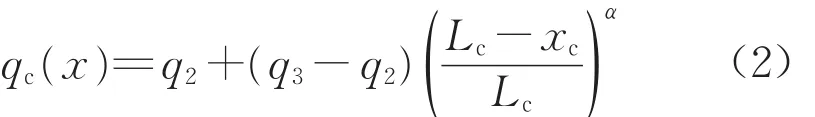
主跨钢梁自重荷载分布为

2.3 计算分析方法

根据基本假设中桥梁施工过程要经历的4个主要阶段，对桥梁结构选取如下三个基本状态进行分析：①最大双悬臂混凝土梁施工状态；②边跨混凝土现浇段合龙状态；③主跨钢梁安装完成的成桥状态。

（1）最大双悬臂状态

混合梁刚构桥的混凝土采用从墩顶处对称悬臂施工，当混凝土梁的悬臂浇筑部分施工完成后，此时结构可简化为如图3所示的最大双悬臂状态，结构整体为静定结构体系，此时自重荷载作用下的梁段墩顶弯矩为

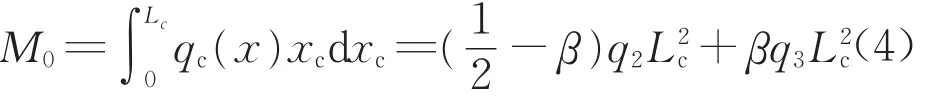
式中：β为梁底曲线等效系数，则

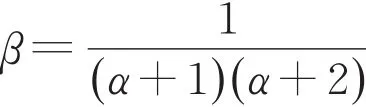
图3 最大悬臂状态Fig.3 Maximum cantilever state

（2）单悬臂状态

当边跨混凝土梁的现浇部分施工完成，并进行边跨合龙后，此时结构可简化为如图4a所示的单悬臂状态，结构整体为一次超静定结构，仅考虑边跨现浇段的自重荷载，采用力法建立简化模型如图4b所示，设边跨支座反力为X。

因此，力法基本方程为

由结构力学知识求得

把图4a中的荷载作用在图4b结构上，得到x1=0处截面的弯矩m表达式如下：

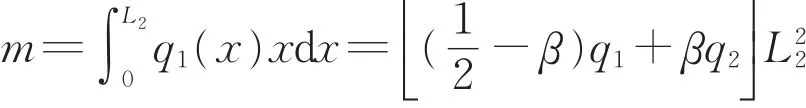
进一步求得

图4 单悬臂状态结构Fig.4 Single cantilever state

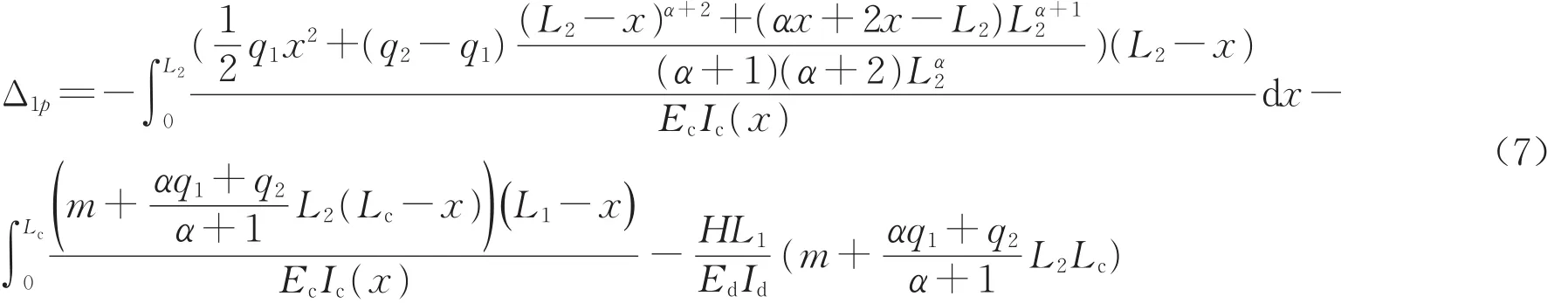
（3）成桥状态

当吊装钢梁完成中跨合龙后，主体结构施工完成，结构可简化为如图5a所示的三次超静定结构，仅考虑钢梁段的自重荷载，采用力法建立简化模型为如图5b所示，设边跨支座反力为X1，跨中水平力为X2，跨中弯矩为X3。

图5 成桥状态结构Fig.5 Bridge in completion state

力法基本方程为

由结构力学知识求得

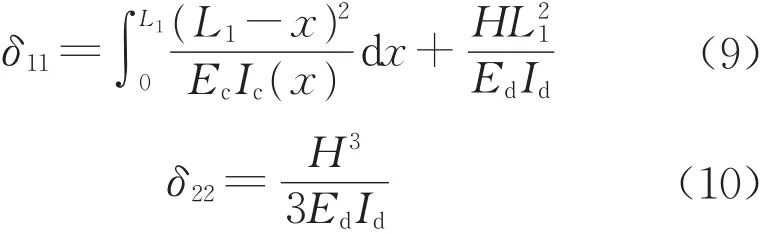
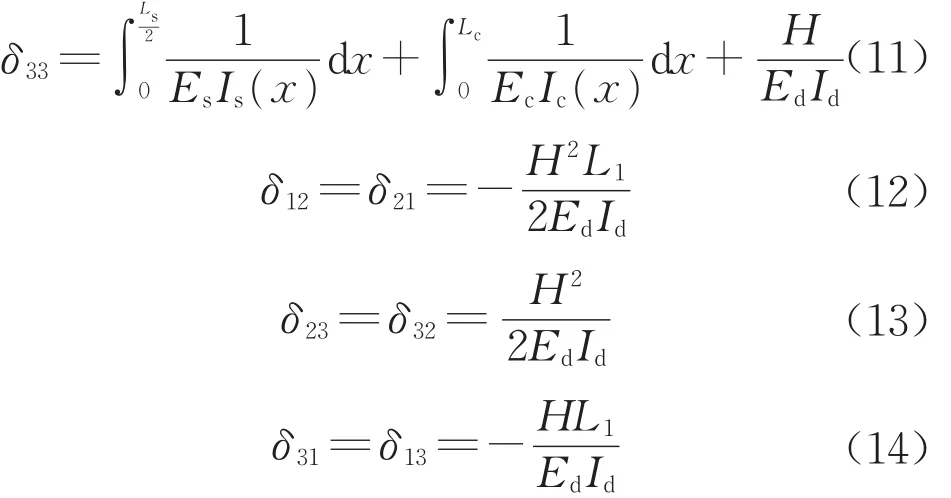
把图5a中的荷载作用在图5b结构上，得到xs=Ls/2处截面的弯矩n表达式如下：

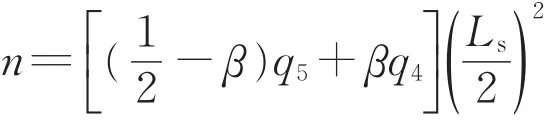
进一步求得

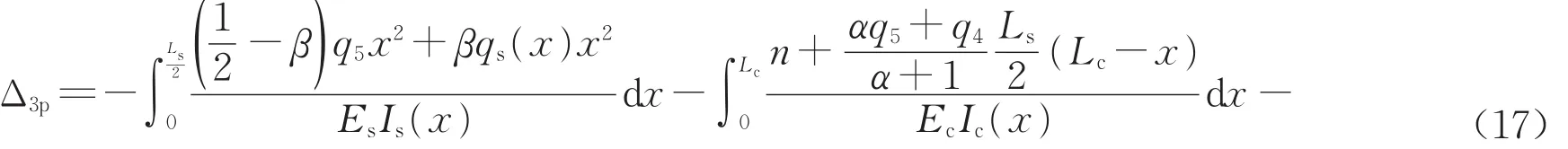
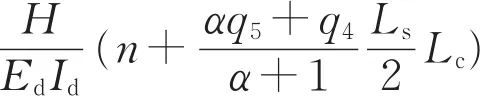
从而得到控制截面的内力最终表达式即

边跨支座反力

B截面弯矩

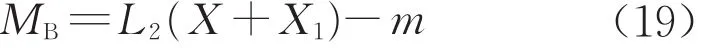
C右截面弯矩

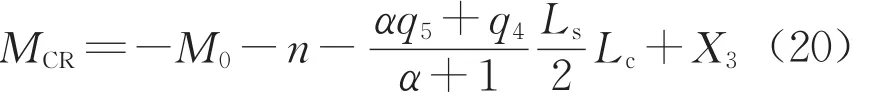
C左截面弯矩

D截面弯矩

E截面弯矩

2.4 简化方法的校验

（1）有限元模型检验

为了校核简化计算方法的计算精度，通过Midas Civil建立了混凝土刚构桥的有限元模型，如图6所示。由于安海湾大桥设计边中跨比λ=135/300=0.45，钢梁长度与中跨长度比μ=108/300=0.36，将这组数据带入理论有限元模型，同时建立单梁有限元模型，详细模拟其施工步骤，但仅施加自重荷载。

图6 桥梁整体有限元模型Fig.6 Overall finite element model of the bridge

依据简化计算模型与有限元模型计算得到的各控制截面弯矩值对比结果如表1所示。可以发现，理论值与有限元值的差异基本在10%以内，二者吻合较好，说明本文推导的简化计算方法具有较高的精度，可以用于桥梁的初步设计阶段的结构内力计算。其中，B截面、C左截面和C右截面误差相对较大的原因可能是在有限元建模的过程中，依据实际设计使顶、底板及腹板的板厚变化较多，而假设中混凝土梁自重集度分布仅与梁高变化相关，二者出现了一定的误差，而钢梁部分自重集度分布的拟合则更符合实际情况。

（2）荷载试验检验

根据《A3标泉厦漳安海湾特大桥主桥荷载试验报告》［13］，安海湾大桥的静力荷载试验主要可分为三类工况，检测边跨最大正弯矩下的边跨合龙处截面、中跨最大正弯矩下的跨中截面以及负弯矩作用下的墩顶1#号块截面的顶板或底板以及腹板的受力，加载方式如图7所示。

图7 荷载试验主要工况加载方式（单位：m）Fig.7 Main load modes of the load test（Unit:m）

荷载试验与简化理论模型的结果对比如表2所示，由于实际测点布置有限，因此仅选取了部分有代表性的测点。可以发现，二者结果十分相近，理论值均比实测值更大，可能由于实桥材料弹性模量与计算模型的有偏差造成的。

表2 荷载试验与简化理论模型计算结果对比Tab.2 Results comparison between load test and simplified theory model με

3 合理钢混结合段位置与边中跨比研究

钢-混凝土混合梁连续刚构桥与传统预应力混凝土刚构桥的最大区别在于中跨中间区域以更加轻质的钢箱梁代替了混凝土梁，钢箱梁与混凝土箱梁通过钢混结合段进行连接，因此在桥梁总体设计中确定钢混结合段的合理位置以及边中跨比对于充分发挥混合梁刚构桥受力性能的优势至关重要。只有最大限度地利用钢梁与混凝土梁各自的优点，方能兼顾结构体系受力合理性和经济节约，同时便于施工操作。

3.1 λ与μ的取值

基于推导的简化分析方法，对比λ、μ不同取值下的控制截面（中跨跨中、墩顶两侧、钢混结合面、边跨合龙处）内力变化规律，从而得到最优λ、μ值。

根据以往的工程经验，国内外大跨径预应力混凝土刚构桥的常用边中跨比为0.50～0.60［14］。由于混合梁连续刚构桥跨中采用了钢箱段，因此边跨混凝土的压重作用不需要太强，从而在混凝土刚构桥的基础上进行一定的折减，取λ范围为0.30～0.60，同时取μ的范围为0.30～0.60，选取增量为0.05进行计算分析。

在λ与μ的变化过程中，要保证能够在悬臂施工结束后，进行边跨合龙及钢箱梁吊装。从而在数学上要满足，使边跨长度不小于0，即

3.2 控制截面弯矩

当λ=0.30，μ=0.40～0.60时，各个控制截面弯矩如图8所示。随着μ的增大，跨中弯矩及边跨合龙处弯矩为正，跨中弯矩变化不明显，但边跨合龙处弯矩呈现显著的增大趋势，钢-混结合处弯矩为负，均逐渐增大。墩顶两侧弯矩为负，随着μ的增大弯矩绝对值在逐渐减少且二者的差值基本恒定。

图8 λ=0.30时控制截面弯矩随μ的变化图（单位：kN·m）Fig.8 Variation of bending moment of key section with μ when λ =0.30(Unit:kN·m)

由于混合梁刚构桥中主梁弯矩最大值发生在墩顶处，而且该位置的数值远远大于边跨合龙处和钢混结合段处的弯矩。因此图9仅给出在不同边中跨比下墩顶附近主梁弯矩随μ的变化图。由图8看出在同一种边中跨比λ下，在墩顶附近的梁截面弯矩绝对值均是随着μ的增大而减少，这是由于钢梁段的增大使得主跨结构的自重减少所产生的。另外在桥梁主跨长度不变的情况下，增加λ值（即增加边跨长度）会使得主梁在墩顶边跨侧的弯矩快速增大，而主梁在墩顶主跨侧的弯矩保持不变，进而导致主梁在墩顶处两侧的弯矩差值也逐渐增大，而且这个差值随μ的增大而增大。由刚构桥的结构形式知，主梁在墩顶处两侧的弯矩差值实际是桥墩受到的弯矩，也就是随着λ值的增加墩顶弯矩的作用方向发生改变并且墩顶承受的弯矩也在增加。

3.3 优化原则

大跨度桥梁中恒载所占的比例要远大于活载对于桥梁结构的布置优化，主要研究恒载作用下结构的内力分布是否合理［14］。因此，本文的主要控制原则为：①边跨支座不出现负反力；②主梁墩顶两侧弯矩平衡或相差不大，提高对称截面的材料使用效率；③满足以上两个条件的基础上，使各个位置的弯矩都相对较小。④满足以上条件后，考虑一定的经济性与可施工性。

3.4 优化过程

通过计算可知，一般情况下边支点反力恒为正，仅在边跨现浇段长度为零这种实际工程中不会发生的工况下，才会为负值。采用墩顶两侧弯矩平衡的原则，由于常用的工程误差精度为5%，而且连续刚构桥中桥墩可以承担一定的弯矩，因此将墩顶两侧弯矩差值比例小于5%作为二者是否接近平衡的评判标准，结果如表3所示。

根据表3中混合梁刚构桥在不同的λ下的μ合理取值范围，以安海湾大桥为例，计算不同λ下使墩顶两侧弯矩平衡的桥跨布置所对应的各截面弯矩值如表3所示。

进一步考虑其余优化控制原则，即各部分弯矩都相对较小，结构弯矩分布均匀，且具有经济性与可施工性。从表4看出λ=0.35时墩顶弯矩明显小于其他两组，主要是在该边中跨比下的跨中钢箱梁长度要明显大于其他两种情况。尽管大节段钢箱梁的整体吊装已有成果的案例［15-17］，但随着钢箱长度增大，吊装设备、施工难度、工程费用及施工风险等也逐渐增大，特别是在混合梁刚构桥中当边中跨比λ较少时，会存在跨中车辆超重时导致边支座脱空的风险。因此λ=0.35时，虽然墩顶负弯矩较小，需要慎重考虑采用该组桥跨布置，以降低桥梁施工和使用中的风险。

图9 不同λ下墩顶附近梁截面弯矩随μ的变化（单位：kN·m）Fig.9 Variation of bending moment of beam near pier top with μ under different λ(Unit:kN·m)

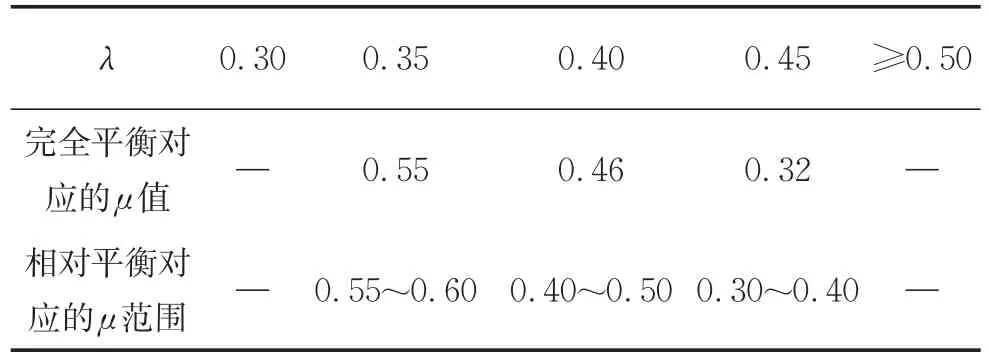
表3 主梁在墩顶两侧弯矩平衡时的λ与μ值Tab.3 λ and μ values for balancing the bending moments of the beam on both sides of the pier top

表4 不同λ的桥跨布置所对应的各截面弯矩值Tab.4 Moments of cross sections by varying λ kN·m

对比λ=0.40与λ=0.45桥跨布置，前者墩顶弯矩仅为后者的76.7%，减小较多。而桥梁其他部位的弯矩均远远少于墩顶处的弯矩，因此推荐采用边中跨比λ取0.40，跨中钢梁与主跨之比μ取0.40～0.50作为混合梁刚构桥的优选方案。该推荐方案结构布置合理、受力性能优越、经济性能适中、施工和运营中的风险小。