超短波多径信号相关干涉仪测向算法

高婕， 牛刚,， 杜太行， 雷正伟

(1.河北工业大学 人工智能与数据科学学院， 天津 300401； 2.32181部队， 河北 石家庄 050000)

收稿日期：2019-12-19

基金项目：国家自然科学基金项目(61601496)

作者简介：高婕(1986—)， 女， 博士研究生。 E-mail: gaojie2011@hebut.edu.cn

通信作者：牛刚(1981—)， 男， 高级工程师。 E-mail: 18032058600@163.com

0 引言

无线电测向是无线电管理、射电天文、电子对抗等领域的常用任务之一，其基本含义是利用无线电测向设备接收空间中的辐射源辐射的电磁信号，并利用模拟或者数字的方法进行信号处理，确定辐射源的方位[1-4]。无线电测向主要以电磁学、天线技术、接收机技术、数字信号处理技术、计算机程序设计等多个方向的理论、方法与技术为基础，同时还需考虑应用场景、架设环境、实现成本等多种因素，是一种实践性强的工程技术。应用场景按照频段进行划分，主要分为短波测向、超短波测向、微波测向等；架设环境主要分为大型固定场地架设、小型固定场地架设、车载(舰载/机载)架设等。实现成本主要受到性能指标、体积质量、架设环境、应用场景等多种因素限制，需要综合考虑。

超短波频段(30～3 000 MHz)是日常中最为常用的无线电频段，例如航空通信、调频广播、对讲机、移动通信等等都在超短波频段范围之中。 对于超短波频段的测向，通常采用干涉仪的方法，主要包括相位干涉仪[5]和相关干涉仪[6-7]，其中，相关干涉仪引入相关处理，有助于克服设备有关的误差，因而得到了最为广泛地应用。相关干涉仪通常分为固定式和车载式两种形式，其中，固定式主要安装于建筑物楼顶、高塔等位置，而车载式则安装在车辆顶部。 受到城市高大建筑物密集的影响，相关干涉仪(尤其是车载式相关干涉仪)在城市环境中受到多径传播[8]的影响较大。 当非直达径与直达径的信号功率相差较小时，相关干涉仪将不能正常工作[1]。

本文着力于在不改变相关干涉仪测向设备软件和硬件技术体制的情况下，利用信号处理算法来克服多径传播的影响，将多径条件下的测向问题转换成为联合稀疏表示数学问题进行求解。

1 超短波相关干涉仪测向设备原理

相关干涉仪测向设备主要用于超短波频段的测向，其主要部件有超短波天线阵列、双通道测向接收机(最为常用)等。

1.1 设备组成

超短波天线阵列通常为圆阵[9-10]，如图1所示，其中1, 2, …,M为M个均匀分布的天线阵元，与阵列中心的距离均为R，超短波信号的入射方向(来波与y轴负轴的夹角)为θ. 天线阵列中内置了开关矩阵，用于天线频段的选择和阵元的选择。

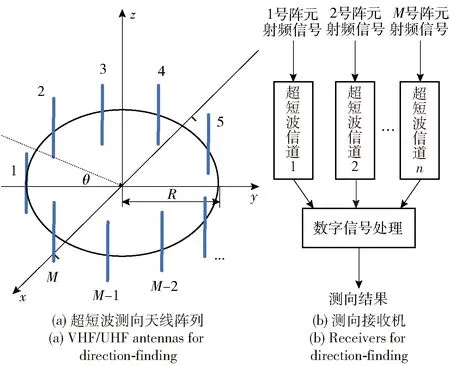
图1 超短波测向天线阵列及接收机示意图Fig.1 Schematic diagram of VHF/UHF antenna array and receivers for direction-finding

双通道测向接收机[11]由两路同步接收通道模块、校准源模块、本振模块、数字处理板卡、单板计算机等模块组成，其中，两路接收通道分别用于接收选通阵元信号(依次选通)和参考阵元信号。

1.2 基本测向算法原理

假设测向天线阵列由M个天线组成，超短波信号的入射方向为θ，那么在理想情况下，第m个天线的电压值分别为

(1)

式中：s(t)为信号时域波形；kλ为波数，kλ=2π/λ，λ为波长。 假设1号天线为参考阵元，其他天线为选通阵元，则选通阵元与参考阵元的复值相位差为

(2)

式中：ψm为第m个选通阵元与参考阵元的相位差。

(2)式中的M-1个方程进行联立，可以实现测向，该方法被称为相位干涉仪。

实际工程应用中，由于非理想天线和设备、布设环境等因素，超短波相位干涉仪的测向效果有待提升[1]。通常采用相关干涉仪的方法来降低这些因素的影响。其基本原理如下：

1)厂内校准。架设发射天线和信号源，将测向设备放置在转台上。记录超短波频段范围内的每一个频点和方向对应的M-1个相位差ejψm，数据库大小与频率点个数和方向个数成比例。

2)正常工作。首先进行测频，读取相应频率的数据库。将测量到的相位差数据矢量与数据库中的每一个矢量进行匹配，最为匹配者为信号方向。通常采用的匹配方式为矢量相关运算，故称为相关干涉仪。

2 多径信号相关干涉仪测向算法

在存在多径传播的超短波信号情况下，只有当直达径的信号功率高于非直达径6 dB以上时，采用矢量相关匹配运算的相关干涉仪才可以正确测出直达径的方向[1]。 本文将提出一种基于稀疏表示(SR)[12]的相关干涉仪测向方法，实现如下两个功能：

1) 测向不受6 dB的直达径与非直达径功率差限制；

2) 同时给出直达径和非直达径的方向。

首先做出如下假设，信号采集模块的IQ信号已经过频域数字滤波，使得输入到测向算法模块的IQ信号中只包含有一个超短波信号及其多径信号。建立多径条件下的超短波信号模型，共有K条路径θ1,…,θK，其中每条路径的复值幅度为p(θk)，那么参考阵元和选通阵元的电压值分别可以表述为

(3)

式中：vm(θk)为第m个选通阵元与参考阵元的天线响应幅度比；nm(t)为噪声。

记幅度比与复相位差的乘积为

cm(θk)=ejψm(θk)vm(θk),

(4)

并记：

(5)

于是，

(6)

假设将整个空域划分成了Q个栅格{φq,q=1,2,…,Q}，栅格密度足够大，并为此栅格建立了幅度比与复相位差的乘积的数据库为

{cm(φq),q=1,2,…,Q}，

(7)

超短波信号的多条路径对应的栅格集合为Ω，于是上述模型可以转化为

(8)

由于信号与噪声之间相互独立，各个阵元的噪声也相互独立，于是选通阵元与参考阵元的测量电压值的互相关为

(9)

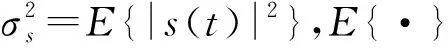
dm=[cm(φ1),cm(φ2),…,cm(φQ)]，

(10)

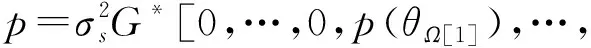
(11)

式中：(·)T表示(·)转置；Ω[k]表示集合Ω的第k个元素。 于是有

(12)

接下来将M-1互相关值组成一个列矢量，

(13)

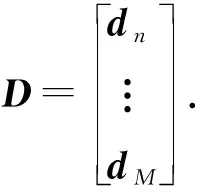
对于移动通信而言，p矢量是时变的，同样，测量到的互相关矢量y也是时变的。对于连续N包数据获得的N个y矢量，有

(14)

对于数目较小的N而言，由于相位干涉仪和辐射源之间几乎保持相对静止，可以认为N个pn矢量(n=1,2,…,N)的非零元素的位置不变。此时，无线电测向问题已经转换为带约束的欠定问题：

已知(M-1)×Q维的矩阵D和N个M-1维的矢量y1,y2,…,yN，求解N个Q维矢量p1,p2,…,pN的联合谱，满足：

1)yn=Dpn；

2)pn为稀疏矢量；

3)pn中非零元素的位置是相同的。

该问题可以利用多个稀疏矢量的联合SR[13-14]的方式进行求解，即

(15)

式中：‖·‖1表示l1范数；ε为预设的门限值。联合谱可以采用下式计算：

(16)

式中：diag(·)代表取出矩阵的对角线元素并构成列矢量；‖·‖F表示Frobenius范数。

3 计算机仿真

假设超短波测向天线阵列半径为0.5 m，阵元个数为9个；数据库的角度步进为1°；接收机通道个数为两个；每次天线开关切换后，用来计算互相关的采样点个数为4 096；入射信号频率为600 MHz；仿真中每一个IQ数据包中的非直达径与直达径信号的相位差为随机相位；本文算法利用16组相邻的数据包进行计算，传统干涉仪方法则使用的是16组的平均相关曲线；本文算法中(15)式的求解采用了通用凸优化数学工具CVX[15-16].

图2给出了本文方法与传统方法的谱图对比，仿真条件是信号只有一条路径，即来自150°方位，功率为20 dBm. 由图2可以看出，本文方法与传统方法均可以正确测向。

图3的仿真条件是存在两个路径：直达径来自150°方位，信噪比为20 dB；非直达径来自180°方位，信噪比为14 dB；二者功率相差6 dB. 由图3可以看出，本文方法与传统方法均可以给出直达径的方向，区别在于传统方法的谱图中无法判定非直达径的方向。传统方法虽然在30°和180°方向都形成了较高的谱峰，但是都比主瓣低了10%以上，应判定为旁瓣，只能保留主瓣的测向结果。

图4的仿真条件是存在两个路径且二者功率相等，直达径来自150°方位，非直达径来自180°方位，图4(a)和图4(b)的信噪比(SNR)为20 dB，图4(c)和图4(d)的SNR为6 dB. 由图4可以看出，传统方法已经失效，而本文方法仍可以正确指示两条路径的方向。

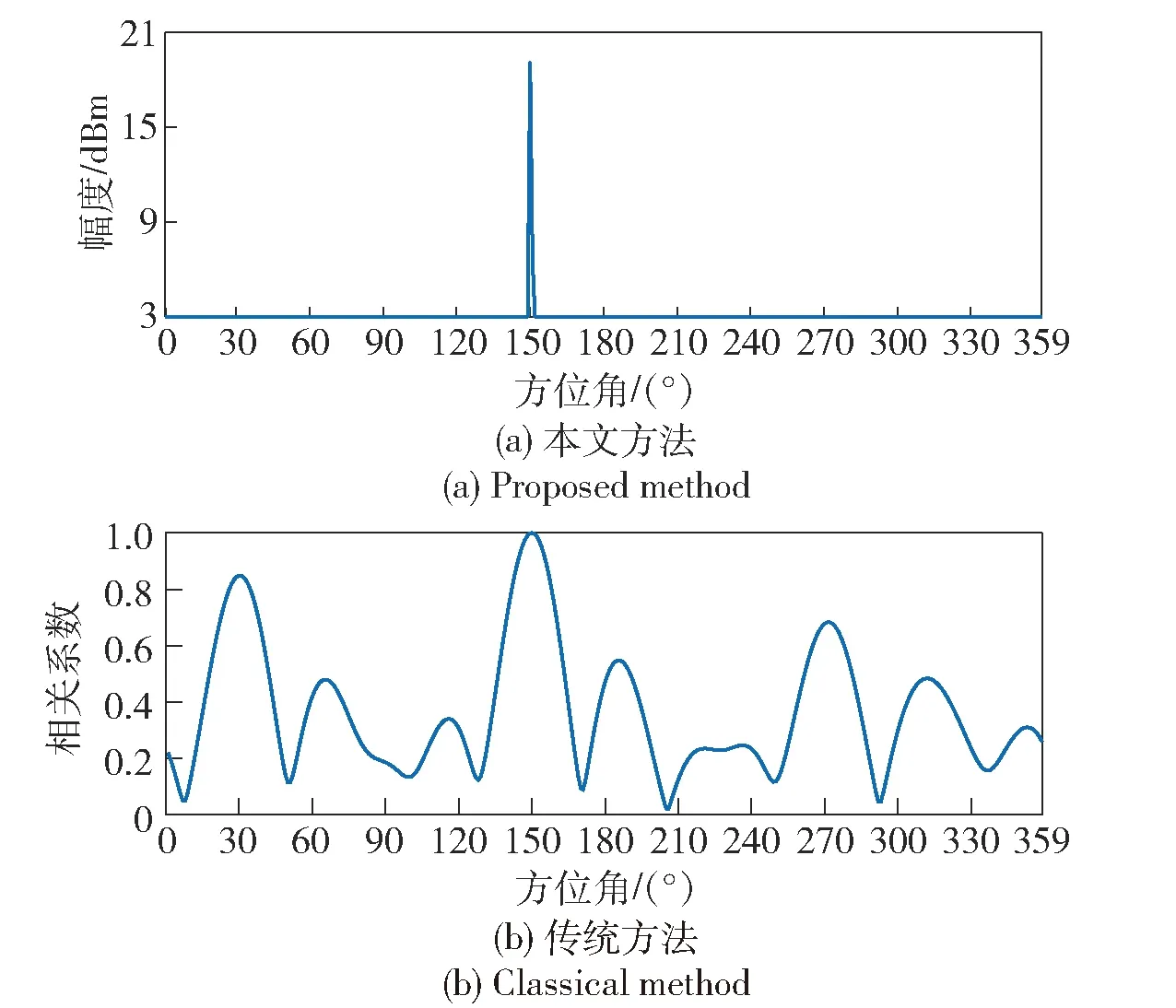
图2 谱图对比：无多径传播Fig.2 Spectra comparison without multipath propagation

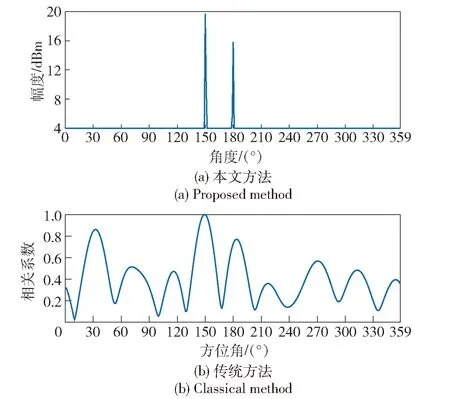
图3 谱图对比：非直达径功率较低Fig.3 Spectra comparison with lower NLOS power

最后考核本文方法的测向精度，角度估计值为3点(峰值、峰值左边点、峰值右边点)线性插值结果，并且以下仿真均由500次独立重复实验计算得出均方根误差(RMSE).

图5的仿真条件是信号只有一条路径，即来自150°方位，SNR由5 dB变化到30 dB. 由图5可以看出，当不存在多径信号的情况下，由于传统方法与最大似然(ML)方法[17]等效，属于统计最优方法，其测向精度优于本文方法，但是二者精度具有可比性。

图6的仿真条件是存在两个路径：直达径来自150°方位，SNR为30 dB；非直达径来自180°方位，SNR由6 dB变化到30 dB，即多径到达与直达路径强度比由-24 dB变化到0 dB. 由于传统方法不具备非直达径测向能力，这里比较了二者对于直达径的测向精度。由图6可知：当多径到达与直达路径强度比低于-6 dB时，传统方法与本文方法都可以准确测向，且测向精度具有可比性；当强度比为-4 dB时，传统方法出现了较为明显的测向误差(约为3°)；当强度比大于等于-2 dB时，传统方法已经失效。

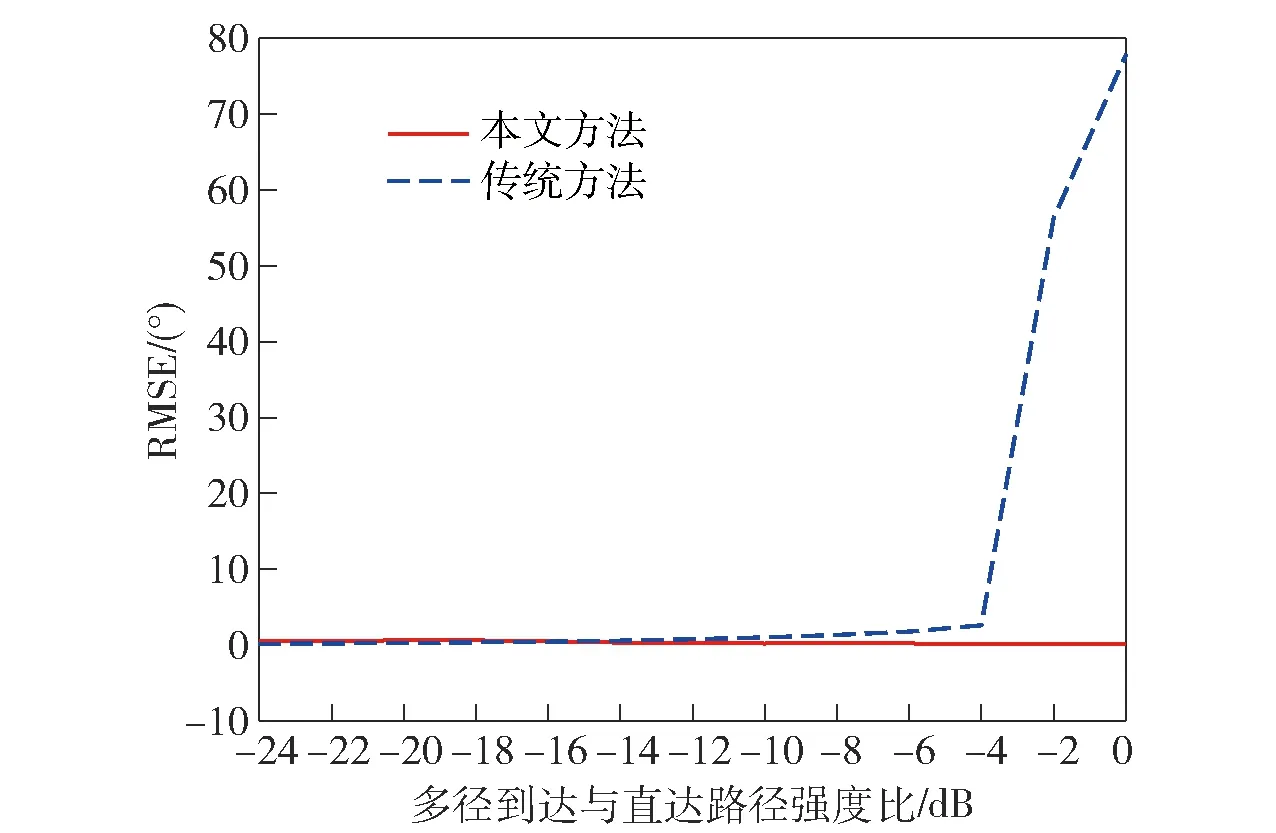
图6 测向精度对比：多径传播Fig.6 Comparison of direction finding accuracies with multipath propagation

4 场地仿真

在微波暗室中开展了验证实验，主要实验器材如下：

1) 对数周期天线2套，频率范围200～2 000 MHz，发射天线增益为7.53dBi@600MHz，3 dB波束宽度约为55°@600 MHz，用于发射直达径和非直达径信号。

2) 矢量信号源一台，用于产生600 MHz二进制相移键控(BPSK)射频信号，输出功率为16 dBm.

3) 功率分配器一个，用于将信号源产生的信号分成两路。

4) 直流(DC)～6 GHz数控射频移相器两个，主要用于调整非直达径信号的相位。

5) DC～6 GHz数控射频衰减器两个，主要用于调整非直达径信号的幅度。

6) 数控转台一个，用于相关干涉仪校准建库。

7) 9阵元测向天线一台，半径为0.45 m，频段为30～800 MHz，接收测向天线采用全向天线振子，天线无源增益为-2dBi@600MHz，方向图不圆度优于3 dB；收发天线相距L=5 m，满足L≥2D2/λ=3.24 m的远场条件，其中D为天线孔径(0.9 m)，λ为波长(0.5 m)；测向天线与两副发射天线构成等腰三角形；功率分配器损耗取6 dB，信号发射的线缆损耗、插入损耗总和取3 dB，自由空间衰减为32.5+20lg600+20lg0.005=42 dB，信号接收的线缆损耗、插入损耗总和取3 dB，接收信道链路增益为40 dB，所以理论上，在衰减器直通的情况下，接收机的数模转变器输入功率为16-6-3+7.53-42-2-3+40=7.53 dBm.

8) 30～3 000 MHz双通道测向接收机。

9) 台式计算机，用于控制移相器、衰减器、转台，以及测向的控制与显示。

10) 网络交换机，用于台式计算机、转台、测向接收机之间的网络连接。

搭建的暗室验证场景示意图如图7所示。

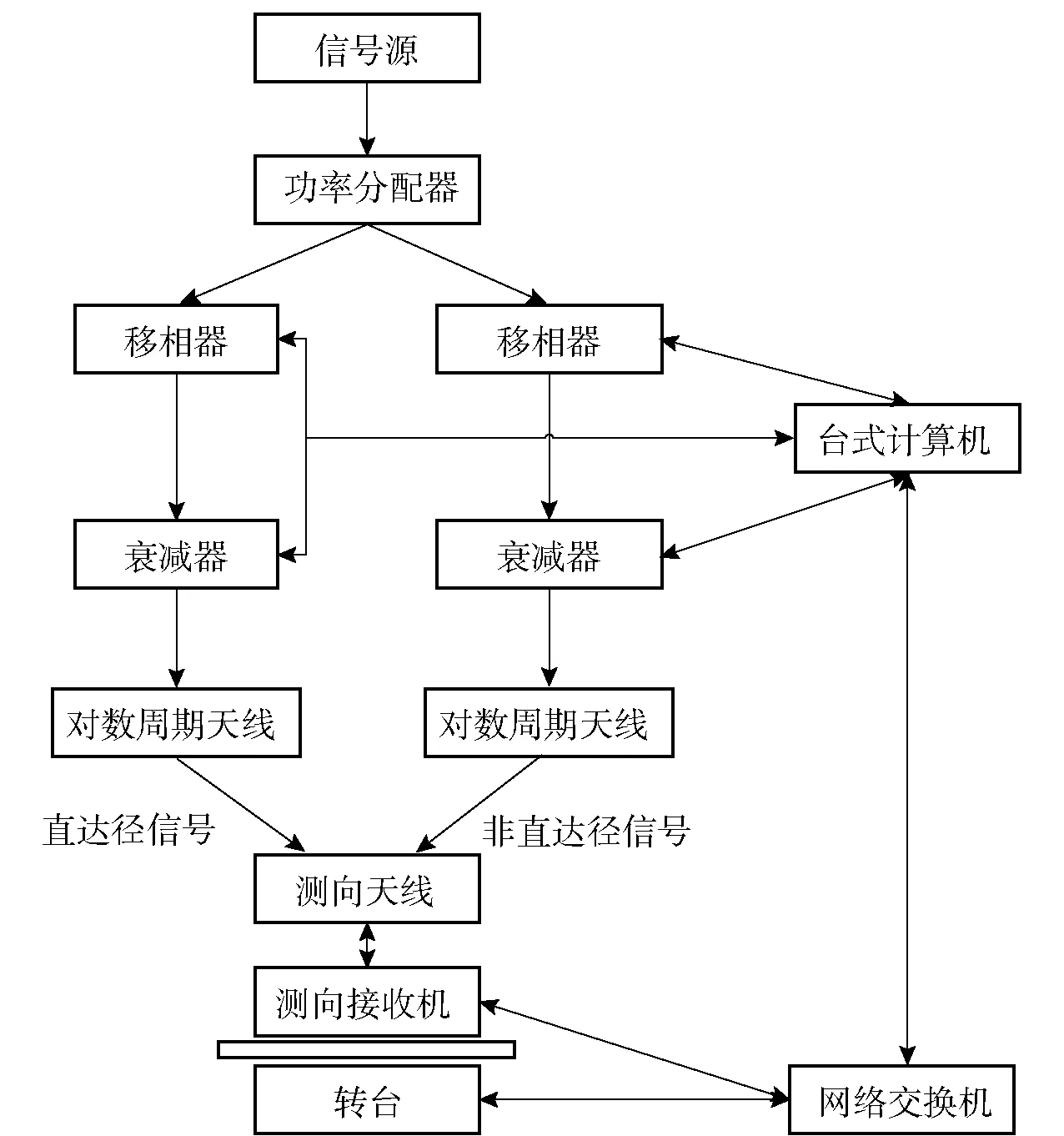
图7 暗室实验的原理框图Fig.7 Schematic diagram of anechoic chamber experiment

如图7所示，两部对数周期天线均为最大波束方向对准测向天线，二者相对于测向天线的零方向的角度仍设定为150°和180°；数据库的角度步进为1°；接收机通道个数为两个；每次测向天线开关切换后用来计算互相关的采样点个数为4 096；入射信号频率为600 MHz的BPSK信号；测向接收机每采集每一包数据，台式计算机控制移相器产生随机移相，控制衰减器随机产生0 dB、2 dB、4 dB、6 dB、8 dB的衰减；为了实现相同的插入损耗和器件响应，在直达径中同样设置了移相器和衰减器，只不过移相和衰减值分别设置为0°和0 dB；本文算法利用128组相邻的数据包进行计算，传统干涉仪方法则使用的是128组的平均相关曲线；本文算法中(15)式的求解采用了通用凸优化数学工具CVX[15-16].

首先考察直达径和非直达径功率相差较大的情况，台式计算机控制移相器产生随机移相，控制衰减器随机产生6 dB、8 dB衰减，实验结果如图8所示。从图8可以看出，两种方法均可以正确给出直达径的方向，而传统方法无法给出非直达径的方向。

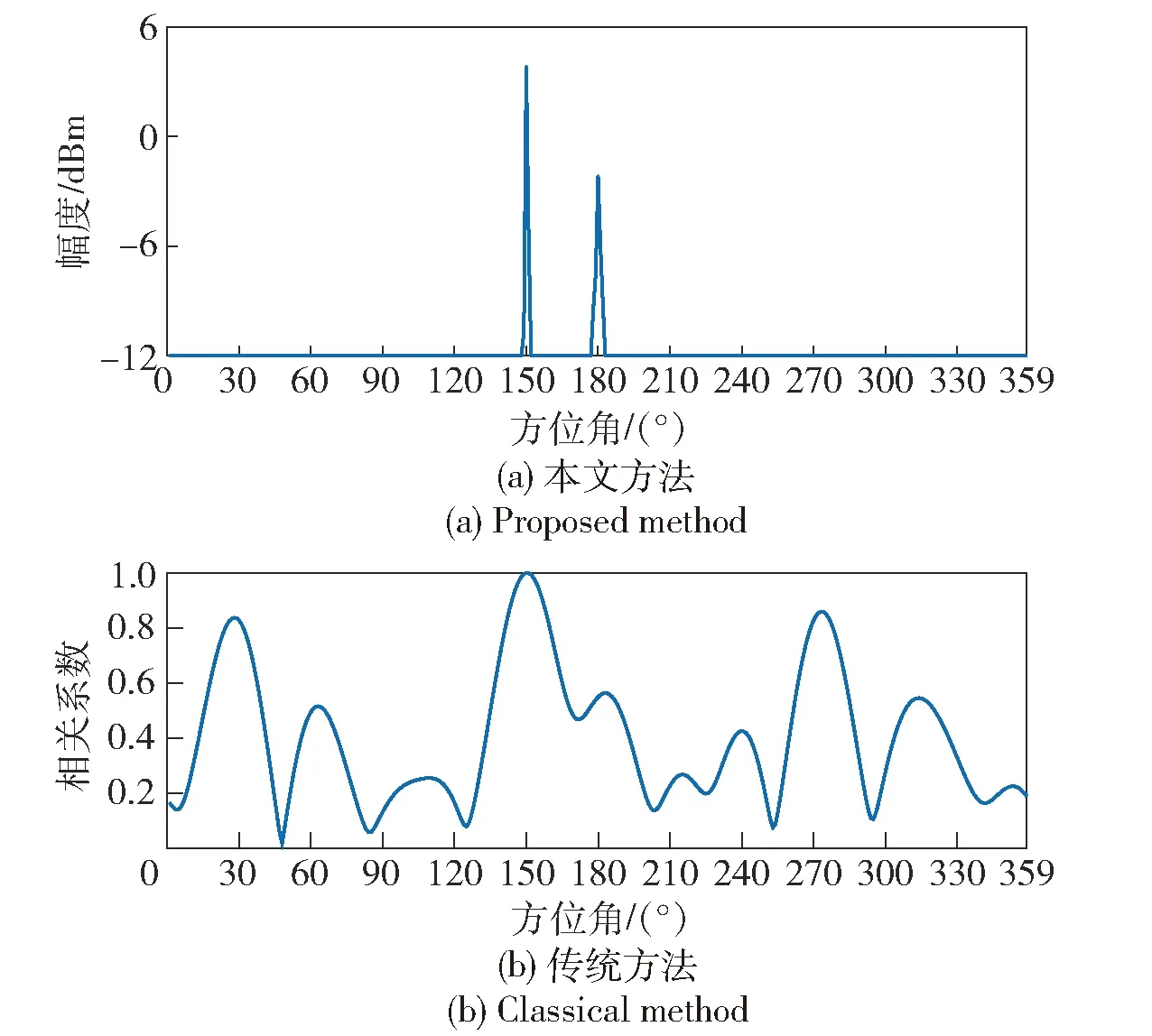
图8 谱图对比：非直达径功率较低Fig.8 Spectra comparison with lower NLOS power

然后考察直达径和非直达径功率相近的情况，台式计算机控制移相器产生随机移相，控制衰减器随机产生0 dB、2 dB衰减，实验结果如图9所示。从图9中可以看出，本文方法可以正确两个路径的方向，而传统方法在两个路径方向和实际上不存在的二者的合成路径方向都显示了等高的谱峰，只能判定为3条路径，测向失效。

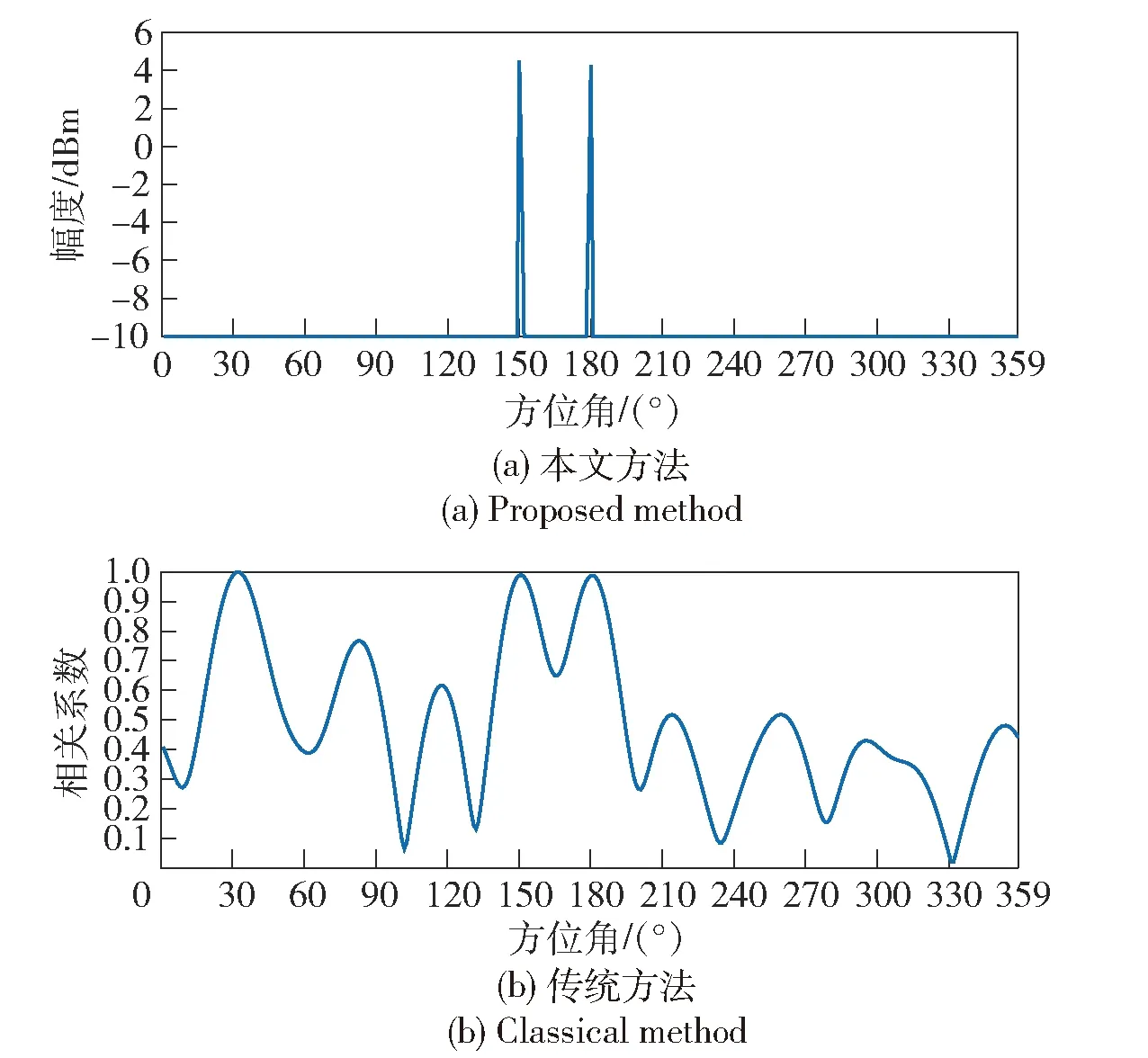
图9 谱图对比：相近功率多径Fig.9 Spectra comparison in the presence of multipath signals with similar powers

5 讨论

在第3节和第4节中，本文分别通过计算机仿真与暗室实验对本文算法的性能进行了验证。在实际环境中，还需要考虑环境温度变化等因素，具体分析如下：

1) 环境温度变化导致射频接收通道一致性的改变：由于相关干涉仪采用的是双通道接收机而不是多通道接收机，这种附加相位差会导致互相关矢量整体上附加相同的相位差，不影响测向结果。

2) 环境温度变化导致频率出现小范围漂移：相关干涉仪的数据库随着频率是缓慢变化的，在超短波频段的数据库频率步进通常超过1 MHz，一般接收机不会出现如此大的频率漂移。

3) 环境温度变化导致天线阻抗匹配发生变化：阻抗虽然不再是50 Ω，导致天线增益有所变化，但是一般情况下变化很小，而且是对于每一个阵元都是一致的，对测向没有影响。

4) 环境温度变化导致系统噪声的变化：最终会导致SNR的改变，进而改变测向精度。提高SNR可以从多个方面入手，例如：一是选用环境适应性高的元器件(例如恒温晶振、低噪声放大器等)；二是采用良好的整机热设计以降低设备自身发热和环境温度的影响；三是选定合适的模拟和数字中频处理带宽以刚好能够覆盖信号带宽即可；四是在满足信号环境不发生改变的情况下尽量采集更长的IQ点数。

5) 环境温度变化导致系统灵敏度的变化：不同阵元上的信号衰落是不一样的。有可能在环境温度较高，系统灵敏度严重下降的情况下，某些阵元上的信号电平已经过低，甚至低于灵敏度。此时需要判定每个阵元上的信号质量，SNR过低的阵元将不再参与测向计算。

6 结论

1) 本文为超短波相关干涉仪测向体制提出了一种新的测向信号处理算法，与传统算法相比，新算法可以在存在相近功率的非直达径信号条件下进行测向并给出每条径的方向。

2) 新算法目前采用的是通用凸优化数学工具进行求解，未来的工作可以放在设计专用优化方法上，以提升算法运算效率。