基于条件深度循环生成对抗网络和动作探索的行星轮轴承剩余寿命预测
2021-01-08于军刘可郭帅于广滨郭振宇
于军, 刘可, 郭帅, 于广滨, 郭振宇
(1.哈尔滨理工大学 先进制造智能化技术教育部重点实验室, 黑龙江 哈尔滨 150080;2.矿冶过程自动控制技术国家重点实验室, 北京 100089;3.哈尔滨理工大学 自动化学院, 黑龙江 哈尔滨 150080;4.中国船舶重工集团公司第703研究所 蒸汽轮机事业部, 黑龙江 哈尔滨 150078)
0 引言
因具有传动比大和结构紧凑等特点,行星齿轮箱已广泛应用于直升机、风力发电机和坦克车等机械设备中[1-2]。复杂恶劣的工作环境会增加行星轮轴承故障的风险[3]。这种难以预料的故障可能导致整个设备突然失灵,甚至造成巨大的经济损失。因此,行星轮轴承剩余寿命预测对保障机械设备可靠运行和避免事故发生具有十分重要的意义。
近年来,国内外学者对典型旋转机械的剩余寿命预测问题进行了深入研究[4],并提出了一些颇具代表性的轴承剩余寿命预测方法。这些方法主要分为3类:物理模型法、统计模型法和人工智能法。
物理模型法通过建立基于失效机理的数学模型,描述机械设备的退化过程。与材料特性相关的模型参数可通过专门的实验或有限元分析方法获得。典型的数学模型包括有限元模型、Paris模型[5]、动力学模型等。物理模型法虽然能实现轴承剩余寿命的准确预测,但在模型建立过程中需满足多种假设,难以建立精确的剩余寿命预测模型。而且模型参数的确定依赖人工经验,从而限制了物理模型法的广泛应用。
统计模型法根据基于经验知识的统计学模型预测机械设备的剩余寿命。统计模型中的随机变量常用于描述各种变化源的不确定性,因此,统计模型法能有效描述退化过程的不确定性并准确估计机械设备的剩余寿命。常用的统计模型包括自适应回归模型[6]、随机系数模型[7]、Wiener过程模型[8]、全阶乘模型[9]等。随机变量的引入明显提高了用于描述各种退化过程的模型柔性。然而,统计模型法的不足在于预测效果严重依赖历史数据,导致剩余寿命预测得不准确。另外,随机变量的概率分布需满足多种假设,从而限制了统计模型法的实际应用。
人工智能法通过智能技术识别机械设备的退化状态,而非构建物理模型或统计学模型。人工智能法能解决难于构建物理模型或统计学模型的复杂机械系统剩余寿命预测问题。因此,人工智能法在轴承的剩余寿命预测领域受到极大关注。典型的人工智能法包括人工神经网络[10]、模糊逻辑系统、支持向量机(SVM)[11]、Gaussian过程回归[12]等。人工智能法无需额外的先验知识或精确的解析模型,通过历史数据识别退化过程。因此,人工智能法在复杂系统的剩余寿命预测中具有重要的应用价值。
行星轮轴承不但自转,还绕太阳轮公转。其内圈安装在行星轮轴上,相对于行星轮轴固定不动;外圈安装在行星架上,随着行星架的旋转而旋转。从故障位置到传感器的时变振动传递路径,使采集到的行星轮轴承振动信号具有非静态的特点。此外,由于受到转速和负载变化的影响,行星齿轮箱在变工况条件下运行,所采集到的振动信号往往是非线性的。行星轮轴承的疲劳寿命试验耗时且投入巨大,仅能获得有限的行星轮轴承全寿命周期样本。行星轮轴承的剩余寿命预测需要大量训练样本,导致行星轮轴承的剩余寿命预测模型无法得到充分训练。因此,小样本和变工况下行星轮轴承的剩余寿命预测准确率较低。
本文将门控循环单元神经网络(GRUNN)与条件生成对抗网络(CGAN)相结合,构建一种深度学习模型,使该深度学习模型具有较强的非静态和非线性信号处理能力,并能解决小样本情况下行星轮轴承的剩余寿命预测问题,同时利用动作探索(AD)技术改善学习决策质量、减少迭代次数。
1 理论基础
1.1 门控循环单元神经网络
循环神经网络(RNN)通过建立单元间的循环连接,记忆任意长度序列的输入数据[13]。RNN的关键在于t时刻输出ht是由当前输入xt和前一时刻输出ht-1决定的。计算公式为
(1)
式中:W″和H为转换矩阵;b″为偏置向量;f为非线性激活函数。
然而,常规RNN的训练过程可能导致梯度消失或梯度爆炸。为缓解这一问题,Chung等[14]开发了一种可实现状态记忆和信息获取的门控循环单元(GRU),用于构成GRUNN. GRU的结构如图1所示。重置门r用于调整新输入与之前记忆的合并,更新门z用于调控之前记忆中保留的信息。GRU中的转换函数定义如下:
zt=σ(Wzxt+Vzht-1+bz),
(2)
rt=σ(Wrxt+Vrht-1+br),
(3)
(4)
(5)

图1 GRU的结构Fig.1 Architecture of GRU
1.2 条件生成对抗网络
生成对抗网络(GAN)是2014年由Goodfellow等[15]提出的一种生成式模型,一经提出就成为人工智能领域的研究热点之一。GAN并不是一个完整的网络模型,而是一种网络训练框架。该框架仅有两个组成部分:生成器和判别器。GAN的核心思想来源于博弈论中的零和博弈,将生成器和判别器看作博弈双方。生成器用于生成尽量服从真实数据分布的样本,判别器用于判断输入样本是真实样本还是生成样本。优化目标是通过对抗机制达到纳什均衡。
CGAN是在GAN基础上加入了额外的条件c(如类标签),通过额外的条件c指导数据的生成过程[16]。CGAN的模型结构如图2所示。输入随机噪声n的同时输入相应条件c,使生成器G生成尽量服从真实数据分布Pdata(x)的样本G(c,n);在条件c的指导下,判别器D判断输入样本是真实数据x还是生成样本G(c,n)。目标函数V(D,G)为
En~Pn(n)[lg(1-D(G(n|c)))],
(6)
式中:Pn(n)表示先验噪声分布;Ex~Pdata(x)[lgD(x|c)]表示将真实数据x与条件c输入判别器D获得是否为真实数据的概率;En~Pn(n)[lg(1-D(G(n|c)))]表示随机噪声n与条件c输入生成器G产生的生成样本,判别器D判别其为真实数据的概率。生成器G尝试最小化目标函数,判别器D尝试最大化目标函数。
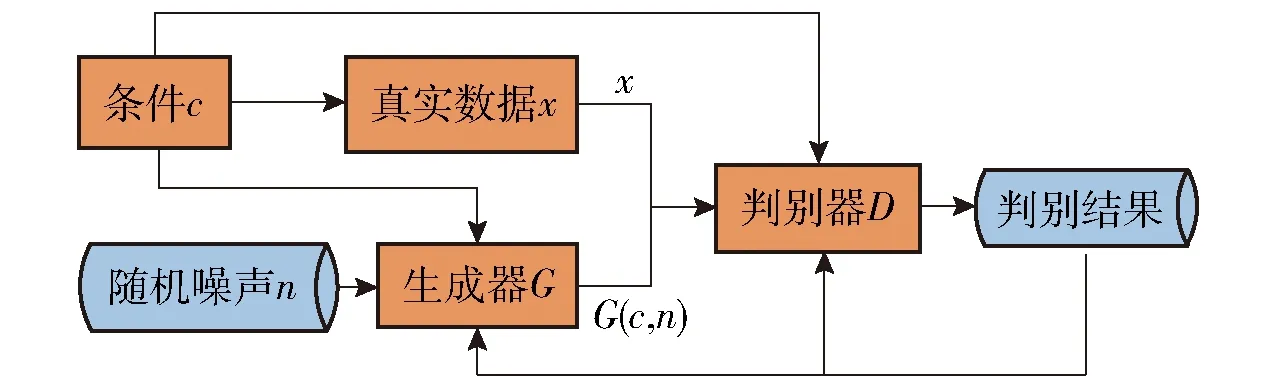
图2 CGAN的模型结构Fig.2 Model structure of CGAN
1.3 动作探索
作为一种重要的机器学习方法,强化学习(RL)已广泛应用于控制工程、故障诊断和图像处理等领域。它采用 “尝试与失败”机制,使智能体在与环境的交流中学习,利用评价性的反馈信号实现决策的优化[17]。RL可用于解决智能体如何学习近似最优行为策略的问题。RL的过程是一个试探与评价的过程,其基本框架如图3所示。当环境状态为st时,智能体执行一个动作at,获得一个奖励ut,并将该奖励反馈给智能体。环境从而转移成一个新的状态st+1. 为了最大化长期的累积奖励,智能体选择一系列后续动作。t时刻的累积折扣奖励定义如下:
(7)
式中:γ为折扣因子,可对成本函数进行一定折扣[20],γ∈(0,1];ut+k+1为t+k+1时刻的奖励[18]。
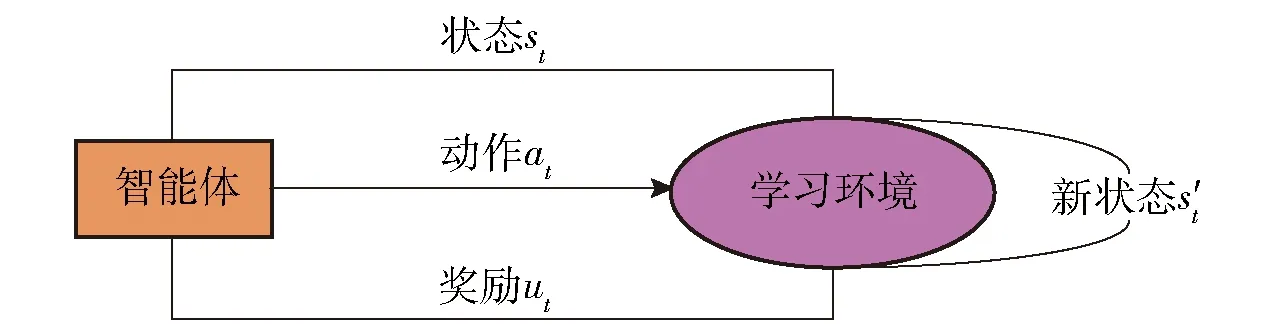
图3 RL的基本框架Fig.3 Basic framework of RL
AD是一种RL算法[19]。为寻求最优动作集,AD将动作集分离到每一个状态。通过探索和评估新动作并执行,AD不仅避免了动作集的限制、改善了学习决策质量,还减少了获取最优策略的迭代次数。AD采用成本函数p衡量新动作的复杂度。智能体从状态st转移到状态st+1的成本为p(st,st+1)。此外,AD采用潜在函数φ(st)评估新动作。φ(st)可用于精确搜索目标、构造奖励值以及降低采样复杂度。采用了潜在函数φ(st)评估新动作可适用性的公式为
γp(st,st+2)φ(st+2)>(1+δ)γp(st,st+2)φ(st+1),
(8)
式中:δ为松弛变量,代表探索新动作的保守程度。对于深度神经网络Q,AD通过最小化损失函数方式获得神经网络的参数集。损失函数的定义为

(9)

(10)

(11)
(12)
θi+1为第i+1次迭代时当前网络Q的参数集,θi+j为第i+j次迭代时当前网络Q的参数集,α为学习率。通过(11)式和(12)式可周期性地更新网络参数θ和θ-. 在智能体执行动作后,根据当前环境,在满足(13)式的情况下更新动作集。
[p(st,st+2)<∞]∧[a(st,st+2)∉At(st)]∧
[γp(st,st+2)φ(st+2)>(1+δ)γp(st,st+2)φ(st+1)],
(13)
式中:At为t时刻的动作集。
2 行星轮轴承剩余寿命预测方法
2.1 行星轮轴承剩余寿命预测框架
作为一种新型RNN变体,GRUNN不但能处理时序数据或前后关联数据,还能缓解常规RNN在训练过程中可能导致的梯度消失问题。另外,GRUNN特殊的门结构能够有效地解决长短时间序列上的变化问题。因此,可利用GRUNN从非静态和非线性的行星轮轴承振动信号中提取故障特征,用于变工况下行星轮轴承的剩余寿命预测。CGAN是GAN的一个扩展,它通过额外条件c指导数据的生成过程,利用生成器G生成新样本。因此可将行星轮轴承所处阶段看作额外的条件c,指导生成器G生成服从真实数据分布的新样本,从而增加训练样本数量,解决训练样本不足的问题。如果将GRUNN与CGAN相结合,构建一种条件深度循环生成对抗网络(C-DRGAN),则该深度学习模型将具有较强的非静态和非线性信号处理能力,并能解决小样本情况下行星轮轴承的剩余寿命预测问题。作为一种新颖RL算法,AD将动作集分离到每一个状态,寻求最优动作集。通过探索和评估新动作,不仅改善了学习决策质量,还减少了迭代次数。如果将剩余寿命预测问题看作智能体的决策过程,则该智能体将根据目标导向政策采取行动,以取得最佳长期回报。多元线性回归(MLR)分类器[21]是一种传统预测模型。对于非静态和非线性信号,MLR无需繁琐的迭代训练过程与参数调整,能获得精确的预测结果。因此,提出一种基于C-DRGAN和AD的行星轮轴承剩余寿命预测方法。方法框架(见图4)为:构建C-DRGAN,从非静态和非线性信号中提取故障特征;采用基于AD的训练算法训练C-DRGAN,提高收敛速度,降低训练时间;根据训练后的C-DRGAN,利用MLR分类器预测测试样本中行星轮轴承的剩余寿命。
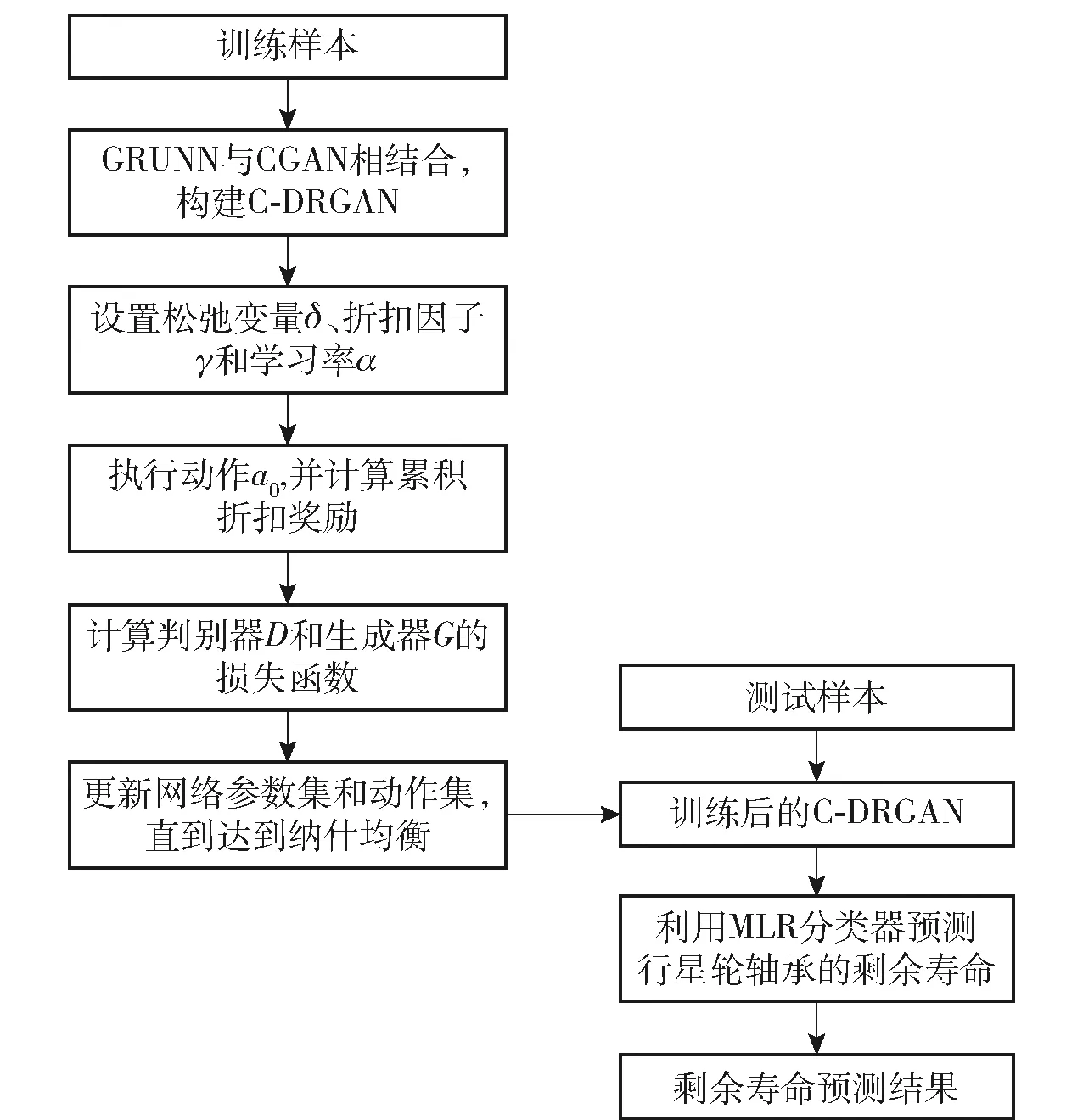
图4 行星轮轴承剩余寿命预测框架Fig.4 RUL prediction framework of planet bearings
2.2 条件深度循环生成对抗网络
如果将GRUNN与CGAN相结合,构建一种深度学习模型,则该模型将同时具备二者的优点。基于这个思路,本文开发一种C-DRGAN. 其模型结构如图5所示,它主要由条件c、生成器G、判别器D和MLR分类器组成。真实数据x为训练样本。随机噪声n与条件c为生成器G的输入。生成器G由一个GRUNN构成。生成器G的输入为随机噪声n. 输出为服从真实数据x分布的生成样本G(c,n)。生成器G在条件c的指导下,利用随机噪声n生成服从真实数据分布的新样本G(c,n)。判别器D由一个GRUNN构成。判别器D的输入为真实数据x和生成样本G(c,n),输出为提取的故障特征。这些故障特征作为MLR分类器的输入,MLR分类器的输出为预测结果。该结果用于计算奖励ut,并反馈给生成器G. 在本文中,真实数据x为行星轮轴承全寿命周期训练样本。条件c为行星轮轴承所处阶段,指导生成器G生成服从真实数据分布的行星轮轴承全寿命周期样本,增加训练样本数量,解决行星轮轴承剩余寿命预测时训练样本不足的问题。判别器D用于提取行星轮轴承的故障特征。MLR分类器根据输入的故障特征,预测行星轮轴承的剩余寿命。根据预测结果计算奖励ut,并利用采用基于AD的训练算法调整生成器G和判别器D的网络参数。

图5 C-DRGAN的模型结构Fig.5 Model structure of C-DRGAN
2.3 基于AD的训练算法
RL中,动作集通常是固定的。即使新的动作被发现,这些新动作也是根据原动作集来描述的。然而,能改进智能体表现的新动作,很可能既不包含于原动作集,也无法根据原动作集来描述。因此,通过探索和评估新动作,利用AD寻找最优动作集。如果将剩余寿命预测问题看作智能体的决策过程,则该智能体可根据目标导向政策采取行动,以取得最佳长期回报。为了改善学习决策质量,减少迭代次数,AD可用于训练C-DRGAN。因此,给出一种基于AD的训练算法。主要步骤如下:
步骤1设置松弛变量δ、折扣因子γ和学习率α. 初始化状态s0、动作a0和动作集A0.
步骤2设置dropout率,并将dropout技术应用于C-DRGAN,防止过拟合现象的发生。
步骤3执行动作a0,观察环境新状态st+1,根据(7)式计算累积折扣奖励。
步骤4根据(14)式计算判别器D的损失函数,
(14)
式中:Lc为类标签的损失误差;Ld为真实标签的损失误差;Θ为判别器D的参数集。
步骤5根据(15)式计算生成器G的损失函数,
(15)
式中:Lg为真实标签的损失误差;Θ′为生成器G的参数集。
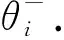
步骤7根据(13)式搜索并评估新动作,更新动作集。
步骤8对下一时刻重复步骤3~步骤7, 直至判别器D和生成器G达到纳什均衡。
3 试验验证
3.1 数据获取
为了验证所提方法的有效性,进行了行星轮轴承加速疲劳寿命试验。图6为行星轮轴承加速疲劳寿命试验台,主要由驱动电机、行星齿轮箱、负载电机和数据采集系统组成。行星轮轴承为NJ304EM圆柱滚子轴承。试验中通过电路控制负载电机产生3种负载(3 000 N·m、4 000 N·m和5 000 N·m),驱动电机的输出转速分别为400 r/min、600 r/min和800 r/min. 因此,可获得3种行星轮轴承运行工况:第1种(800 r/min和3 000 N·m)、第2种(600 r/min和4 000 N·m)、第3种(400 r/min和5 000 N·m)。行星齿轮箱上方的加速度传感器用于采集行星轮轴承运行时的振动加速度信号,采样间隔为10 s,采样频率为25.6 kHz,采样时间为0.4 s. 当振动加速度信号幅值超过80g时,停止试验。

图6 行星轮轴承加速疲劳寿命试验台Fig.6 Accelerated fatigue life test rig for planet bearings
3.2 试验结果

(16)
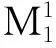

图7 行星轮轴承的全寿命周期振动信号Fig.7 Full lifecycle vibration signal of planet
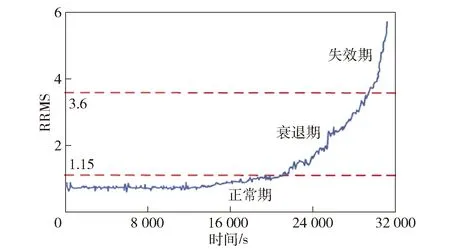
图8 行星轮轴承的RRMS值随时间变化曲线Fig.8 RRMS curve of planet bearing over time
使用的程序开发框架为Tensorflow1.1.0,编程语言为Python. 计算机配置为8核i7-6700处理器,16 GB内存。根据3种运行工况下的6组行星轮轴承全寿命周期训练样本,构建用于行星轮轴承剩余寿命预测的C-DRGAN. 该模型由具有2个GRU层的生成器G、具有两个GRU层的判别器D和一个MLR分类器组成。GRU层的神经元数目设为240,输入数据为45×45矩阵。通过基于AD的训练算法,采用训练样本训练C-DRGAN. 噪声比例设为0.3,松弛变量δ设为0.1,折扣因子γ设为0.9,dropout率设为0.1,学习率α设为0.001. 根据训练后的C-DRGAN,利用MLR分类器预测测试样本中行星轮轴承的剩余寿命。由于MLR分类器的输出为包含多个元素的列向量,该列向量的元素用于拟合测试样本的RRMS值随时间变化曲线。均方根误差(RMSE)是一种常用的轴承剩余寿命预测方法效果评价指标。为了与其他方法进行对比,本文采用由RMSE计算获得的预测准确率评估本文提出方法的效果。预测准确率的计算公式为
(17)
式中:eRMSE为均方根误差;yI和I分别为第I个检查点剩余寿命的真实值和预测值;N为检查点个数。3种运行工况下行星轮轴承的剩余寿命预测准确率如表1所示。从表1中可以看出,负载越大,转速越高,预测效果越好。当负载电机产生5 000 N·m负载且驱动电机的输出转速为400 r/min时,测试样本预测准确率超过98%. 主要原因在于从较大负载和较高转速行星轮轴承的训练样本中获取的故障特征更具特点,有助于预测测试样本中行星轮轴承的剩余寿命。另外,在小样本情况下每种运行工况的平均准确率均超过96%. 这是因为该方法在行星轮轴承所处阶段的指导下,利用生成器G生成大量新样本,从而解决MLR分类其训练不充分的问题。因此,该方法能在小样本情况下准确地预测行星轮轴承的剩余寿命。

表1 3种运行工况下行星轮轴承的剩余寿命预测准确率Tab.1 RUL prediction accuracies of planet bearings underthree operating conditions
3.3 对比分析
因行星轮轴承的剩余寿命预测准确率主要受GRU层神经元数目的影响,神经元数目对预测准确率影响的对比分析如下。改变第1个GRU层神经元数目,且第2个GRU层神经元数目为第1层的一半。第1个GRU层神经元不同数目下的预测结果如图9所示。从图9中可以看出,训练样本准确率可达100%,测试样本准确率超过95%. 但随着第1个GRU层神经元数目的增加,训练时间逐渐延长。主要原因在于C-DRGAN的计算复杂度逐渐增加,延长了训练时间。当第1个GRU层神经元数目超过350时,测试样本准确率保持稳定,而训练时间明显增加。综合考虑预测准确率和训练时间后,将第1个GRU层神经元数目设定为350.
当第1个GRU层神经元数目设为350时,改变第2个GRU层神经元数目。第2个GRU层神经元不同数目下的预测结果如图10所示。由图10可见,测试样本准确率先逐渐提高,然后保持稳定。当第2个GRU层神经元数目达到200时,测试样本准确率达到98.43%. 因此可将第2个GRU层神经元数目设定为200.

图9 第1个GRU层神经元不同数目下的预测结果Fig.9 RUL predicted results with different neuron numbers of the first GRU layer

图10 第2个GRU层神经元不同数目下的预测结果Fig.10 RUL predicted results with different neuron numbers of the second GRU layer
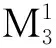
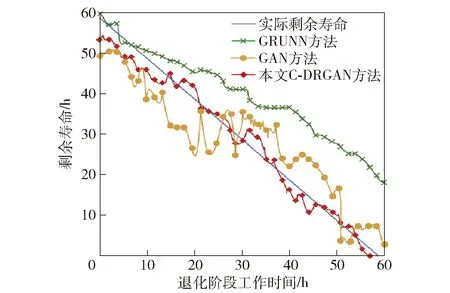
图11 行星轮轴承的剩余寿命预测结果Fig.11 RUL predicted results of planet bearing
为了研究本文C-DRGAN方法的收敛性,分别采用Adam优化算法、基于行动者- 评论家(AC)的训练算法和基于AD的训练算法训练C-DRGAN. 在Adam优化算法中,dropout率设为0.1,学习率α设为0.001,两个矩估计指数衰减率β1和β2分别设为0.9和0.99,数值稳定常数ε设为10-8. C-DRGAN的模型结构和基于AD训练算法的参数设置如前所述。基于AC训练算法的参数设置与基于AD训练算法的相同。预测准确率与迭代次数之间的关系曲线如图12所示。从图12中可以看出,当迭代次数超过320时,基于AD训练算法的预测准确率便趋于稳定,表明该算法能显著地提高C-DRGAN的收敛速度。主要原因在于该算法避免了动作集的限制,使智能体根据目标导向政策采取行动,以取得最佳长期回报,从而减少了获取最优策略的迭代次数,降低了训练时间。
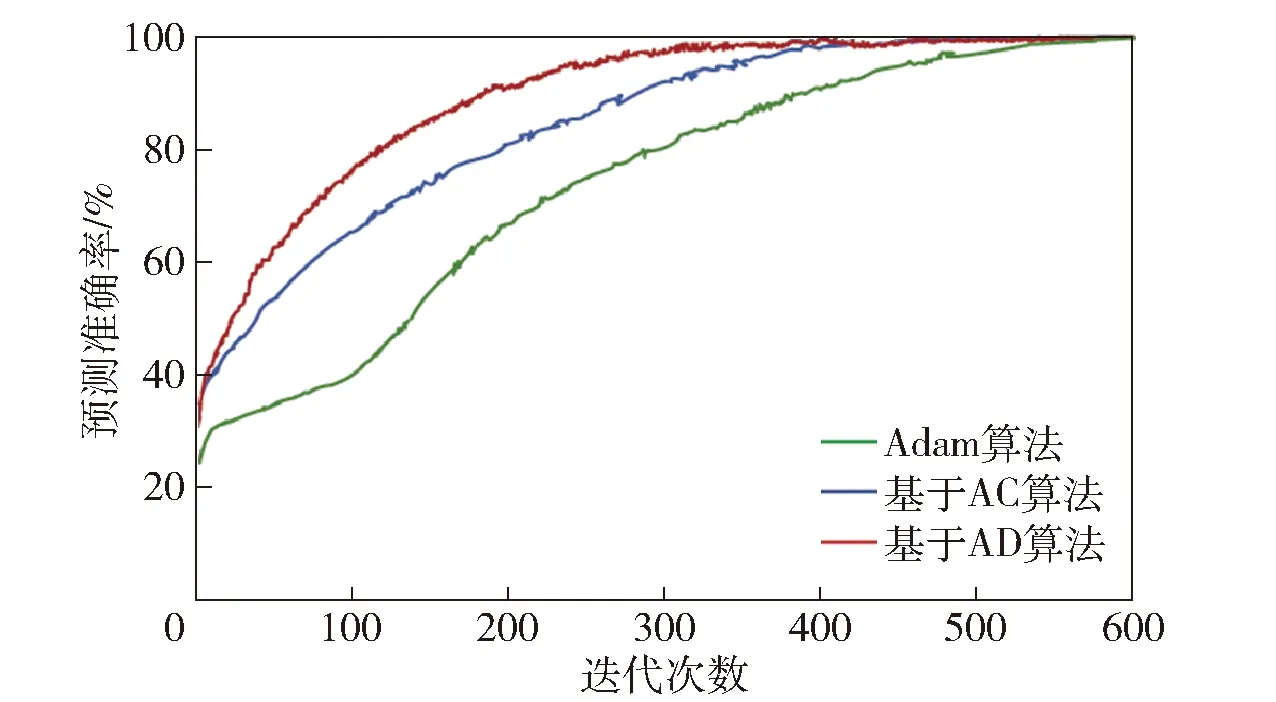
图12 预测准确率与迭代次数之间的关系曲线Fig.12 Relation between RUL predicted accuracy and number of iterations
为了进一步验证本文方法对行星轮轴承剩余寿命预测的效果,将该方法与Paris模型、Wiener过程模型和SVM进行对比。利用时间分段算法训练Paris模型[5];通过极大似然估计算法获得Wiener过程模型的参数[8];采用遗传算法选取SVM的核函数和惩罚参数。训练与测试样本数之比分别为1∶5,1∶2,1∶1和2∶1,4种方法的预测结果如图13所示。由图13可看出,训练与测试样本数之比越大,预测准确率越高。这是由于越多的训练样本可使模型得到充分训练。在不同样本数之比下,该方法均取得最佳的预测效果。原因在于该方法将行星轮轴承所处阶段看作额外的条件,指导生成器生成服从真实数据分布的新样本,从而增加训练样本数量,解决训练样本不足的问题。因此,该方法能取得较高的行星轮轴承剩余寿命预测准确率。
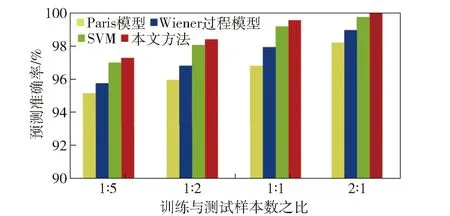
图13 4种方法的预测结果Fig.13 RUL predicted results of four methods
4 结论
1)本文提出的C-DRGAN方法利用CGAN,在已知运行工况指导下生成服从真实数据分布的训练样本,从而在小样本情况下取得出色的行星轮轴承剩余寿命预测效果。
2)C-DRGAN方法利用GRUNN的状态记忆和时变信号的处理能力,从非静态和非线性信号中提取故障特征,解决了变工况下行星轮轴承的剩余寿命预测问题。
3)C-DRGAN方法采用基于AD的训练算法训练C-DRGAN,避免了动作集的限制,使智能体根据目标导向政策采取行动,以取得最佳长期回报,从而减少了获取最优策略的迭代次数,降低了训练时间。
