基于泛函序列时变自回归滑动平均模型的弹箭时变模态参数递推估计方法

余磊， 张永励， 袁梦笛， 刘瑞卿

(西安现代控制技术研究所, 陕西 西安 710065)

0 引言

随着现代战争任务需求的多样化，火箭、导弹的设计也朝着智能化、高速化和大型化方向发展，具有大长细比的柔性制导火箭、导弹不断出现。柔性弹体的固有频率较低，弹体低阶弹性振动容易受到外界干扰激励，给刚性弹体姿态运动的稳定性带来不利影响[1]。因此辨识出弹体的固有频率有助于提高控制的精度并保证任务顺利完成。

一般在飞行试验前，通常采用地面试验方式来确定弹体的固有频率。然而，制导火箭、导弹在飞行过程中，随着构型变化、模块化结构调整和载荷工况变化等过程，使得弹箭成为变结构、变质量、变参数的不确定性对象，传统的时不变结构模态参数辨识方法不再适用，需要开展时变结构模态参数辨识方法研究。

对于弹箭时变结构这类复杂细长柔性体的模态参数辨识方法研究，主要集中于时域法和频域法。由于时域方法辨识的直接性、物理概念的清晰性，工程应用中采用较多。时域法又可分为基于子空间类方法和基于时间序列类方法，其中子空间法即将动力学参数表征到航天器系统的状态方程中，并结合高精度陀螺仪或加速度计等敏感器的测量信息，采用特征值或奇异值分解技术，得到系统矩阵的最小实现。基于子空间的辨识方法得到了广泛应用[2-4]，但是由于其不可避免地要使用特征值或奇异值分解技术，对大型工程结构而言数值复杂性较高，该方法仍有较大的发展空间。

基于时间序列类的方法以描述时间序列的数学模型为研究对象，其中以20世纪80年代在信号处理和控制领域发展而来的时变自回归滑动平均(TARMA)模型[5]最受关注，并成功应用于生物医学信号分析[6]、风速数据建模[7]、桥梁健康监测[8]、齿轮箱故障诊断[9]及风车振动信号分析[10]等诸多领域。Poulimenos等[11]和Spiridonkos等[12]总结了一系列基于TARMA模型的方法，并将这些方法按照时变系数的演化形式分为3类，包括无结构化、随机结构化和确定性结构化。其中，确定性结构化的时变系数演化形式即是将时变序列模型的时变系数用一组基函数展开，进而将时变系数转换为投影空间中的时不变投影系数，这类方法也被称为泛函序列(FS)-TARMA模型。Rao等[13]在1970年基于时间多项式，对时变系数进行展开，这也是FS思想的首次提出。1974年，Mendel等[14]对一般的泛函时间序列模型进行了研究，讨论了时变系数的快变与慢变，为泛函时间序列模型提供了基础。之后，多种多样的基函数被用于描述FS-TARMA模型的时变系数，如Chebyshev多项式[15]、Jacobi多项式[16]、Fourier级数[17]、B样条、无网格形函数[18]等。FS-TARMA模型辨识精度较高，但是在估计过程中需要将总时间段内的时变参数矩阵作为整体进行估计，矩阵维度大，一般采用批量处理，计算效率较低，无法较好地适应弹体飞行模态辨识的快速响应要求。

相对于确定性结构化方法的“笨重”，无结构化方法则利用“短时时不变假设”，即假设在一小段特征时间内系统参数不随时间变化，类似于时间冻结的思想[19]，通过选取合适的特征时间间隔，该假设能够很好地应用于一般的时变结构系统。采用加入时间窗和遗忘因子等[20-21]手段，可以实现高效的模态参数更新，计算效率较高，但是计算精度一般低于批量算法。

本文针对弹箭飞行状态下的时变模态参数辨识问题，基于确定性结构化FS-TARMA模型，提出了一种递推的小波基FS-TARMA时变结构模态参数估计方法。该方法借鉴了无结构化TARMA模型的递推估计思想，有效地改善了FS-TARMA模型的计算效率，并保留了FS-TARMA模型计算精度高的优点。通过一个大型运载火箭时变有限元模型验证了本文提出的算法具有良好的时变模态辨识精度、时变跟踪能力以及较高的计算效率。

1 小波基FS-TARMA模型

1.1 TARMA模型描述

通过振动信号辨识固有频率属于动力学第一类反问题，TARMA模型是基于非平稳时间序列建立起来的离散模型，是解决该类反问题的有效工具。令na和nc分别表示自回归(AR)与滑动平均(MA)的阶数，则TARMA(na,nc)可表示为

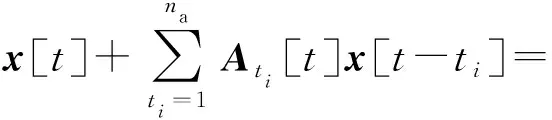
(1)

式中：t为离散化时间；ti为第i阶离散化时间；x[t]∈k×1为非平稳振动响应(多维)信号，k为信号维度；e[t]∈k×1为满足零均值和协方差Σe[t]∈k×k的不相关残差序列；ts为第s阶离散化时间；Ati[t]和Cts[t]分别表示第i阶和第s阶TARMA模型的时变AR和MA系数矩阵。

TARMA模型“时间冻结”模态参数可通过在每一时刻求解如下特征值问题[22]获得，

(pz[t]I-D[t])vz[t]=0,z=1,2,…,kna，

(2)

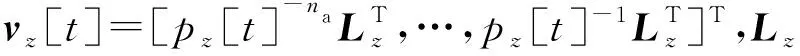
(3)

式中：I为单位矩阵。

更进一步，在Δt的时间间隔下，可得TARMA模型“时间冻结”固有频率和阻尼比分别为

(4)

1.2 基函数选择

采用墨西哥帽小波函数作为基本小波，即母小波，对其进行二进尺度变换和时间轴上的平移。为方便运算，记小波基最大尺度因子等于时间基函数最大维数，可得其小波基为

(5)

式中：l为尺度因子；td为平移因子，td=0,1,…,2j-1；j为时间基函数的展开维数，j=0,1,…,m，m为最大维数。当尺度因子l=0,1,…,m时，ρl,td(t)的伸缩即能拟合慢变和快变的时变系数，从而能够覆盖低频到高频的整个频带。则TARMA模型的时变AR系数矩阵和时变MA系数矩阵可以用墨西哥帽小波基函数展开表示：

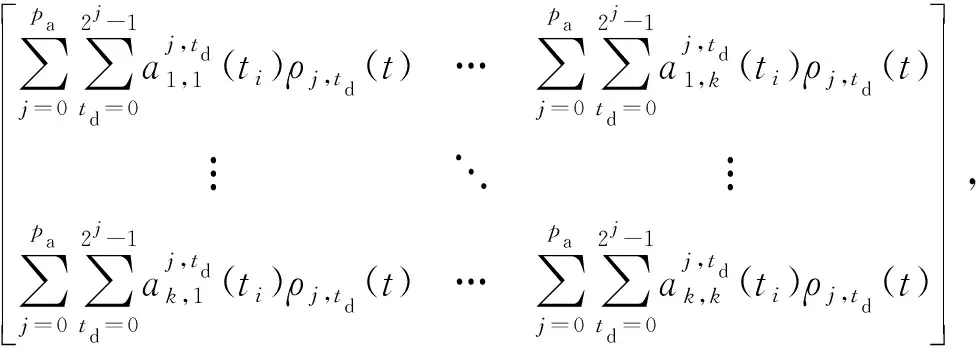
(6)

式中：pa为时变AR系数拟合阶数；pc为时变MA系数拟合阶数。将(6)式代入TARMA模型，可得FS-TARMA模型如下：

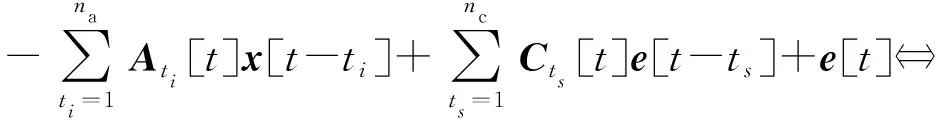
(7)

式中：参数矩阵θT和回归向量φ[t]具有如下形式：

(8)

(9)

式中：⊗为Kronecker积算子；基函数向量ρpa[t]、ρpc[t]为

ρpa[t]=[ρ0,0[t],ρ1,0[t],…,ρpa,2j-1[t]]，
ρpc[t]=[ρ0,0[t],ρ1,0[t],…,ρpc,2j-1[t]].

(10)

由(8)式可知，参数矩阵θT为常数矩阵。通过将TARMA模型参数矩阵表示为一组以墨西哥帽小波基函数的线性组合，可将时变的TARMA模型转化为时不变的FS-TARMA模型，从而把时变模型参数估计问题转化为时不变模型参数估计问题。估计得到的θT代入(6)式中，即可得到系统的模态频率。

2 时变系数的递推估计方法

根据参数估计原理，对(7)式中的参数矩阵θT采用最小二乘准则进行估计，得到估计的费用函数为

(11)

参数矩阵θT的估计为

(12)

式中：arg min (·)为最小化算子，即当费用函数取最小值时，变量的取值；N为辨识数据长度。

不难发现，由于残差序列中存在MA部分，即回归向量φ[t]中包含了残差的过去时刻值，估计参数θT的过程是一个非线性优化问题。针对该问题，Poulimenos等[11]和Spiridonakos等[12]就曾指出，可以采用两步最小二乘方法，将非线性优化过程转化为线性过程进行求解。但是，该估计方法需要将待估参数θT向量化处理，使得计算过程中矩阵维度大，计算耗时长。

为了改善这一问题，可以借鉴无结构化TARMA模型的递推辨识思想。注意到不同时间长度内的θT是不同的，因此θT是关于N的变量，即θT可视为变量θ[t]，利用递推方式，从初始时刻一步步更新θ[t]，最终得到θT的估计值。定义最小二乘费用函数[24]如下：

(13)

式中：τ为离散时间变量。

通过对费用函数进行求导，可得

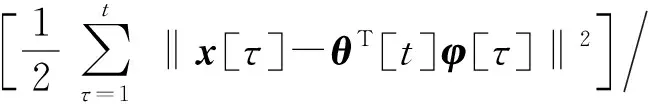
(14)

式中：

(15)

基于(14)式，可以定义协方差矩阵P[t]的形式为

(16)

它的逆矩阵可以表示为

P-1[t]P-1[t-1]+φ[t]φT[t].

(17)

采用矩阵逆定理[25]，(17)式可进一步表示为

(18)

(18)式代入(14)式中，可得

(19)

定义增益矩阵K[t]，信号的一步超前预测[t|t-1]以及一步前向预测误差T[t,t-1]具有如下形式：

(20)

[t|t-1]=T[t-1]φ[t]，

(21)

[t,t-1]=x[t]-[t|t-1] .

(22)

则(19)式可以表达为

[t]T=T[t-1]+[t,t-1]KT[t].

(23)

综上，给出小波基FS-TARMA模型的递推估计格式如下：

(24)

递推估计初始化条件为θ[0]T=0，P[0]=αI，α为模型结构参数。若振动信号的数据长度为N，则参数矩阵θT的估计值为T[N].

3 模型结构选择

第2节给出了模型结构已知情况下的时变模态参数估计方法，在实际情况下，模型结构往往是未知的，需要首先解决模型结构的选择问题。对于本文所提的方法，模型结构可以分为两个子问题：一是模型阶数选择；二是模型的结构参数选择。

递推小波基FS-TARMA模型的阶数选择包括AR阶数na、MA阶数nc、时变AR拟合阶数pa和时变MA拟合系数pc. 一般地，为了控制模型的过拟合程度，需要采用一些准则对拟合程度进行定量描述，本文采用残差平方和(RSS)准则对模型的阶数进行选取。定义FS-TARMA模型的RSS为

(25)

步骤1在搜索区间内对na=nc进行搜索，当RSS曲线取极小值或趋于平缓时，即可确定AR阶数na.

步骤2在确定AR阶数na后，以[0,na]为MA阶数搜索区间，依次对nc进行赋值，当RSS曲线取极小值或趋于平缓时，即可确定MA阶数nc.

步骤3在确定AR阶数na和MA阶数nc后，可假定pa=pc，给定搜索区间，最佳的估计值出现在RSS曲线取极小值或趋于平缓处。

在递推过程中涉及到模型结构参数α的选择，协方差初始矩阵P[0]=αI，其中α一般选取较大的正数(例如α=104)，旨在保证初始阶段的协方差矩阵足够大。

4 数值算例

针对弹箭的仅输出模态分析，本质上是对弹箭动力学响应的分析，弹箭的动力学响应数据一方面来源于实验、工作条件下的实测数据；另一方面来源于弹箭物理模型的数值计算，即动力学的正问题。开展弹箭动力学正问题的研究，不仅可以提供弹箭仿真条件下的动力学响应数据，而且基于力学原理所建立的反映系统物理特性的动力学模型，也对弹箭结构设计与验证具有重要意义。本节以阿里安Ⅴ号运载火箭(以下简称阿里安Ⅴ号)为例进行时变结构动力学建模，建模流程如图1所示。

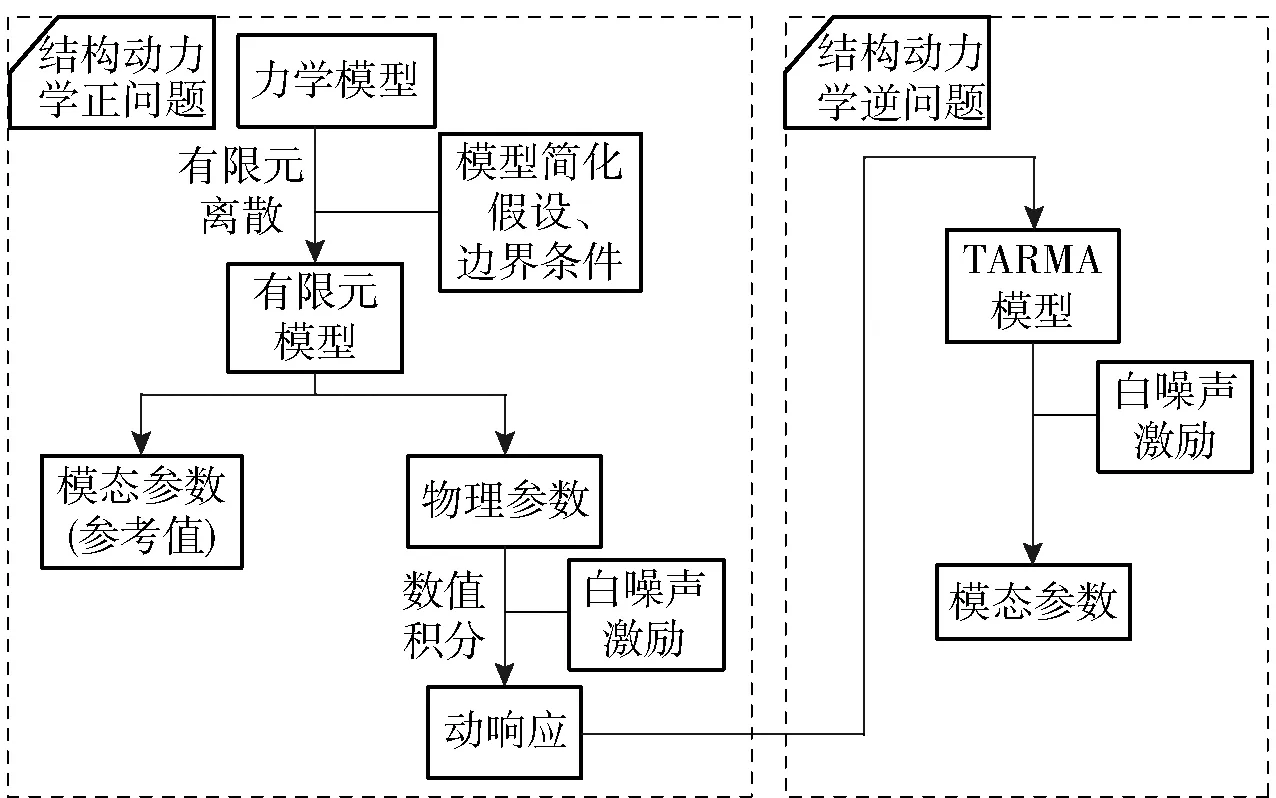
图1 阿里安Ⅴ号时变结构动力学建模流程图Fig.1 Flow chart of time-varying dynamic modelling for Ariane Ⅴ

4.1 阿里安Ⅴ号芯级时变有限元模型

根据振动理论，一个具有nd个自由度的线性振动系统，可以用一个nd维2阶微分方程组来描述如下：

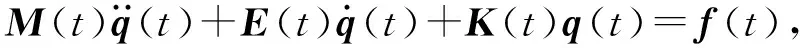
(26)

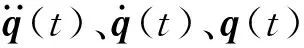
(27)

式中：

(28)

式中：Me、Ee、Ke、fe分别为单元的质量矩阵、阻尼矩阵、刚度矩阵和载荷向量；ρ为质量密度；μ为阻尼系数；N为形函数；D为弹性矩阵；B为应变矩阵；Ve为分析体内所有单元；dV为微元体积。

目前，随着计算机技术的发展，大型复杂有限元模型的动力学离散化一般在商业软件内完成。对于弹箭的时变过程，若每一个瞬时的有限元模型代表当前时刻系统的物理特征，就需要根据时间步长建立大量有限元模型，而商业软件目前并不具备分析时变结构动力学问题的功能。因此，针对弹箭的结构动力学正问题，以阿里安V-versatile芯级为原型，经过调研与合理假设，采用集中质量- 梁模型建立反映运载火箭横向振动特性的有限元模型[26-27]，按照如下步骤进行建模：1)将芯级各部段进行分组编号，并建立几何曲线。2)在得到的每段几何曲线上进行站点划分，站点划分数目应当满足正确描述模型的需求：对于变截面梁，至少需要3个站点以上进行描述；对于等截面梁，则根据长度进行分配，本文模型中对等截面梁单元以0.5 m的尺度进行等比例划分，共得到96个节点、95个梁单元。3)梁截面定义为薄壁圆环，芯级端头和尾段为变截面梁，将结构质量和液体质量分别分配到对应的站点上，结构质量为集中质量，液体质量则在相应的站点上添加对应耦合质量。表1给出了阿里安Ⅴ号芯级的建模信息。图形界面的编写不在本文研究范围内，并聚焦于结构特性上的变化对模态参数的影响，最终建立的阿里安Ⅴ号芯级模型示意图可参考其在有限元软件中的显示结果，如图2所示。

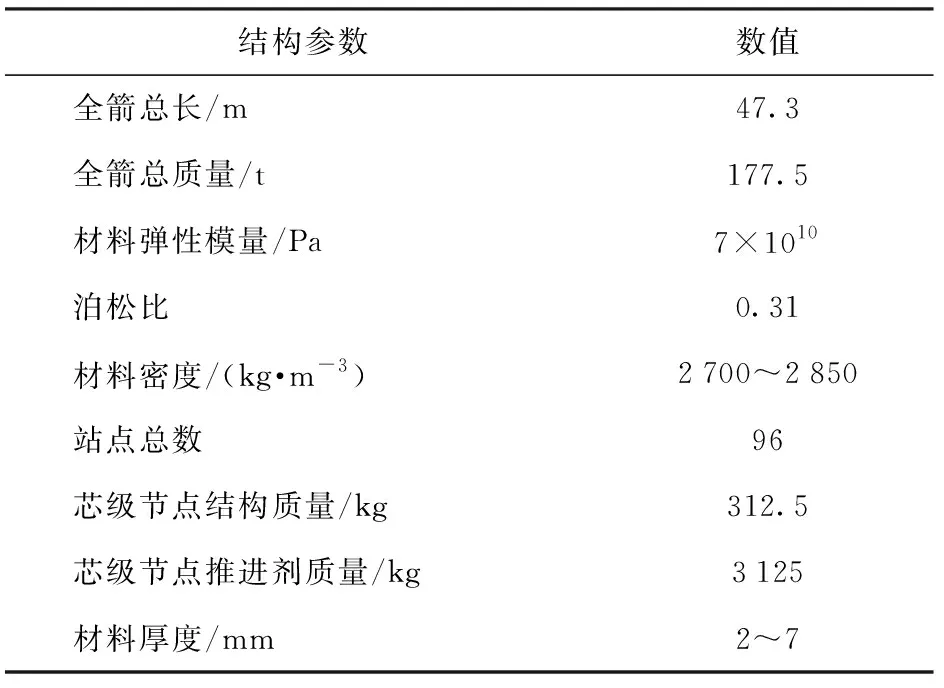
表1 阿里安Ⅴ号芯级建模关键参数Tab.1 Modal structure parameters of Ariane Ⅴ

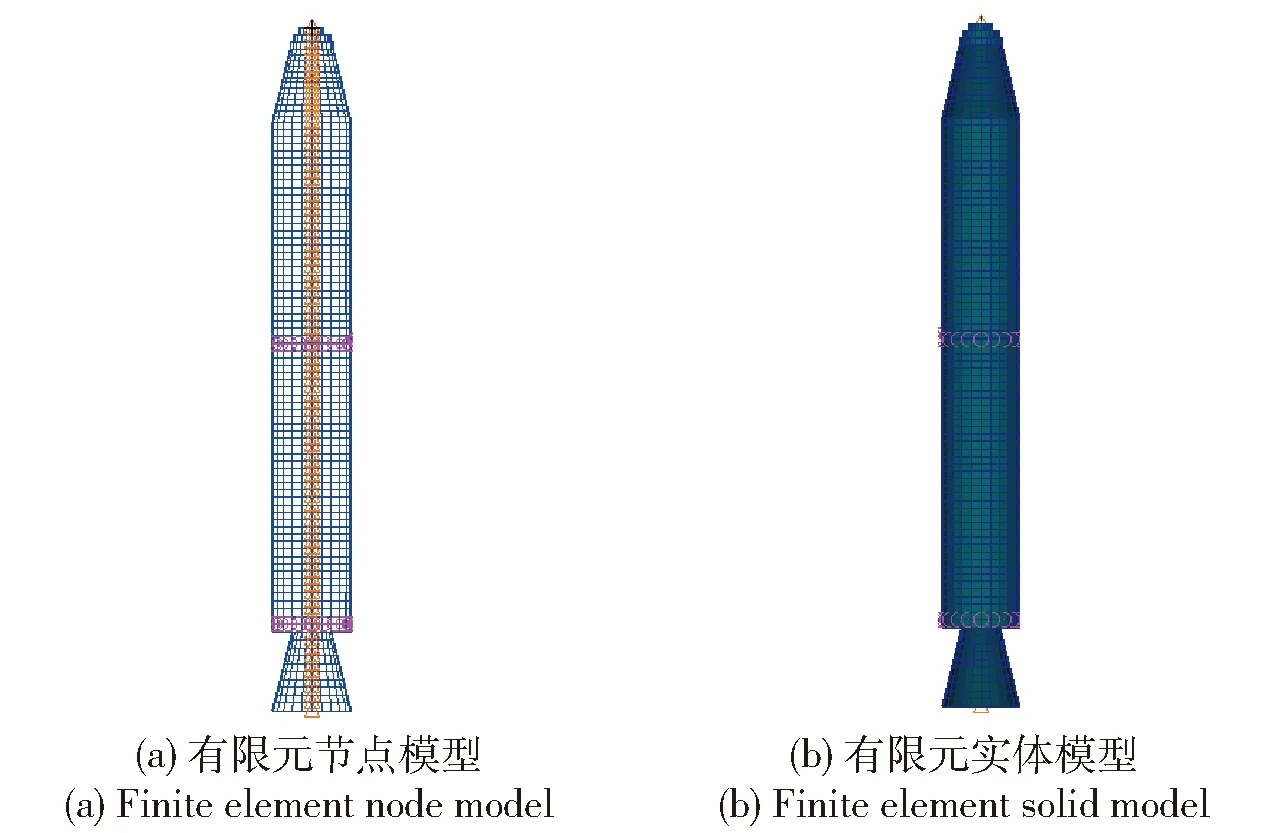
图2 阿里安Ⅴ号芯级有限元模型Fig.2 Finite element model of Ariane Ⅴ

考虑一种质量消耗工况，如图3所示。

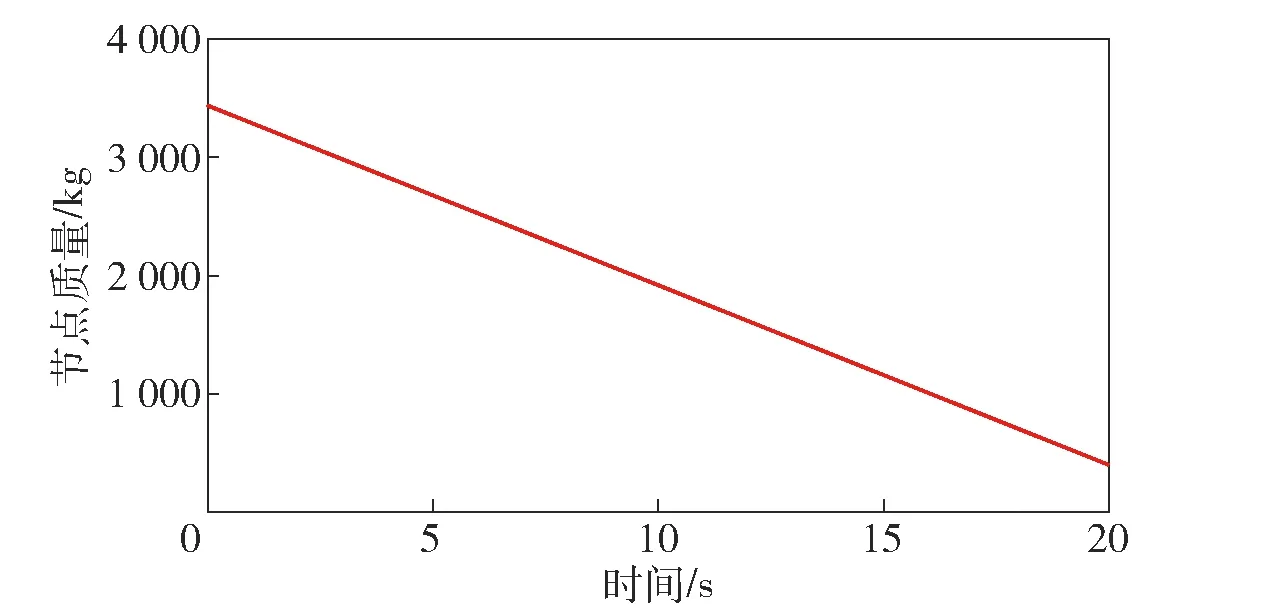
图3 芯级节点质量特性突变规律Fig.3 Time-varying mass feature of the first stage node

采用有限带宽白噪声激励作为激励源，低通截止频率为80 Hz，作用位置为头锥顶点，即整箭几何原点，作用方向沿y轴正向。通过对时变系统进行“时间冻结”分析，以1 000 Hz的采样频率获得整箭的冻结结构集合。在冻结结构集合中，给定底部固支条件，提取阿里安Ⅴ号的整箭冻结结构无阻尼横向振动频率，如图4所示。

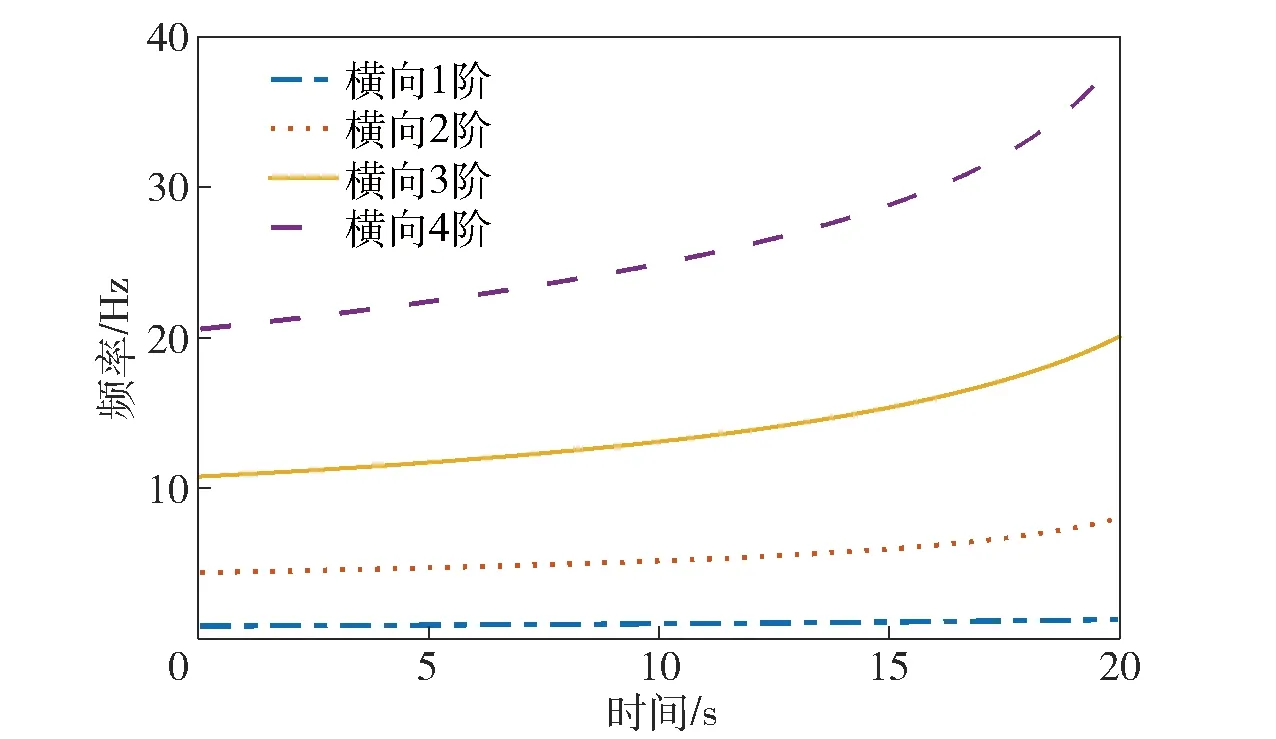
图4 阿里安Ⅴ号“冻结结构”横向模态频率Fig.4 Frozen structure modal frequency of Ariane Ⅴ

使用Newmark-beta数值积分法求解阿里安Ⅴ号时变结构的动响应，并设置比例阻尼E(t)=a0M(t)+a1K(t)，其中a0=0.1,a1=0.001. 提取1号、40号和80号节点的动响应信号如图5所示。

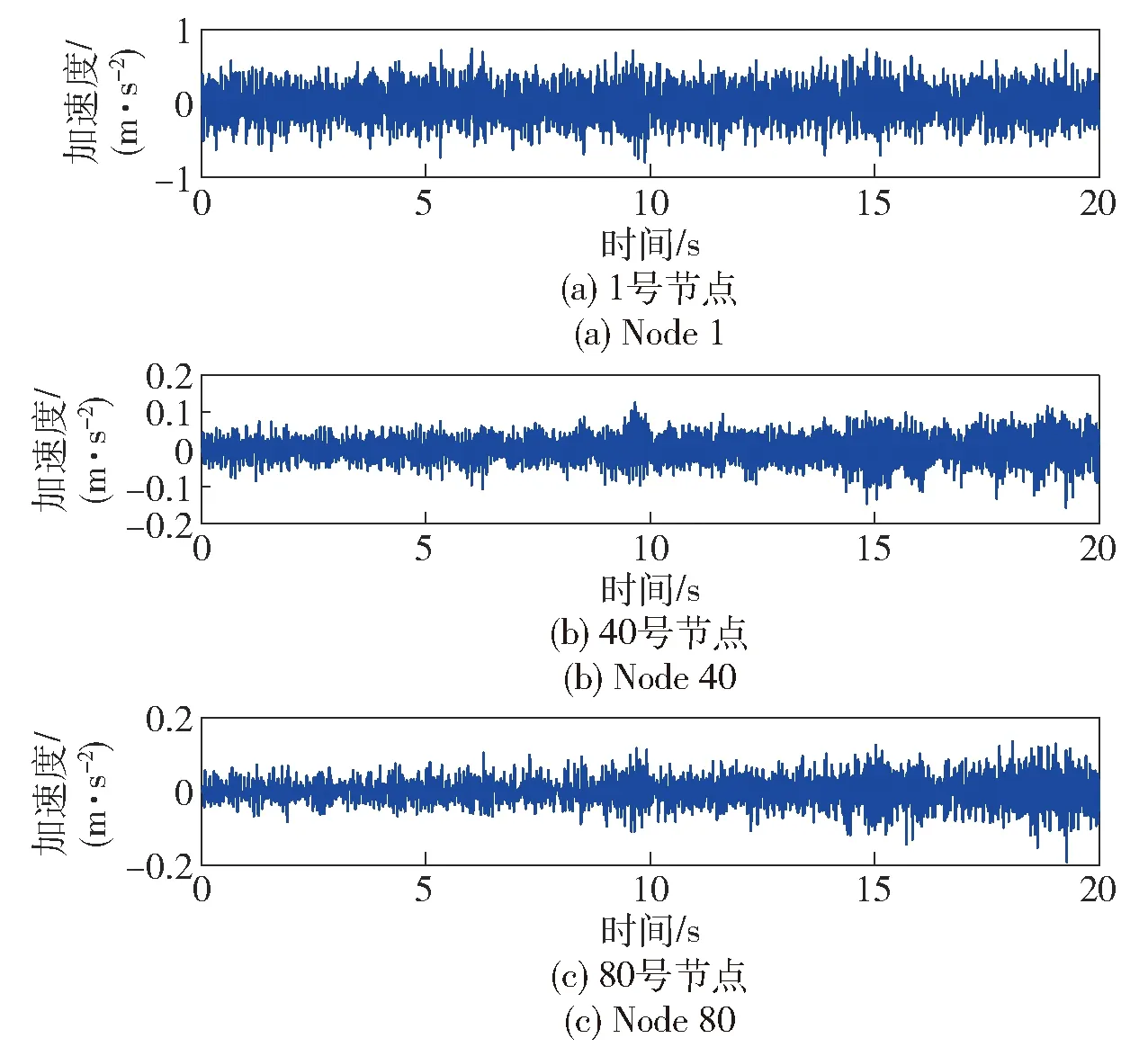
图5 加速度响应Fig.5 Acceleration responses

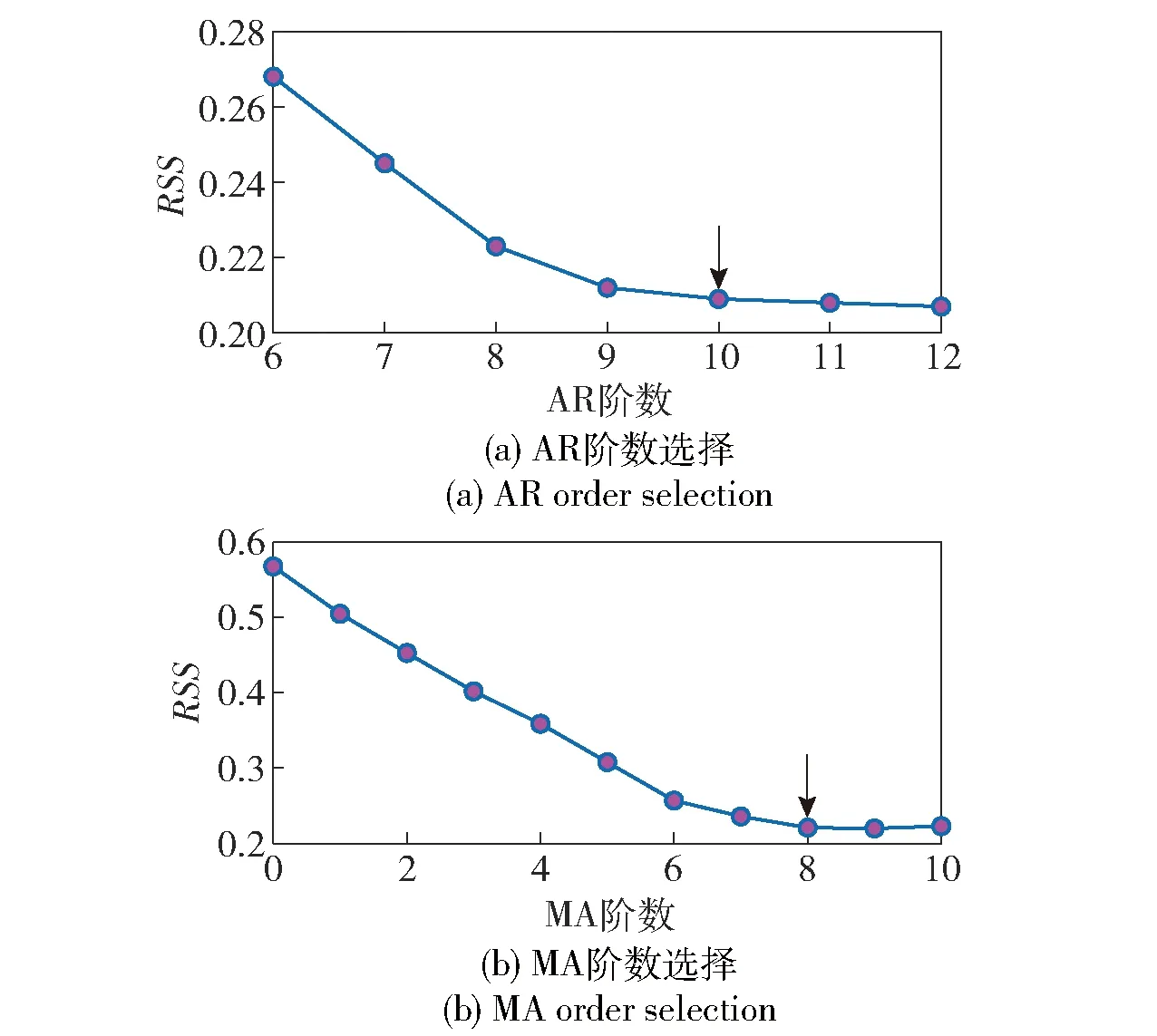
图7 小波基FS-TARMA模型的阶数选择Fig.7 Order selection of wavelet basis FS-TARMA model

取节点1的加速度响应信号作时频分析，以80 Hz的频率进行重采样，采用短时傅里叶变换对重采样后的加速度响应信号进行分析，得到其自功率谱如图6所示。由图6可知，1阶模态的能量与其他阶相比很小，在功率谱中只能看到微弱的峰值。较弱的模态难以用辨识方法辨识出，因此，本文后续只针对运载火箭的第2、3、4阶模态的辨识效果进行讨论。

4.2 模型参数选择与计算结果

根据第3节给出的模型结构选择方法，为简化选择流程，首先给定一组较为完备的泛函空间，取pa=pc=40. 根据RSS准则选取模型的AR和MA阶数如图7所示，即na=10,nc=8. 在初始化参数α=104时，利用节点1到节点96共96组振动响应数据进行分析得到模态参数的辨识结果，如图8所示。

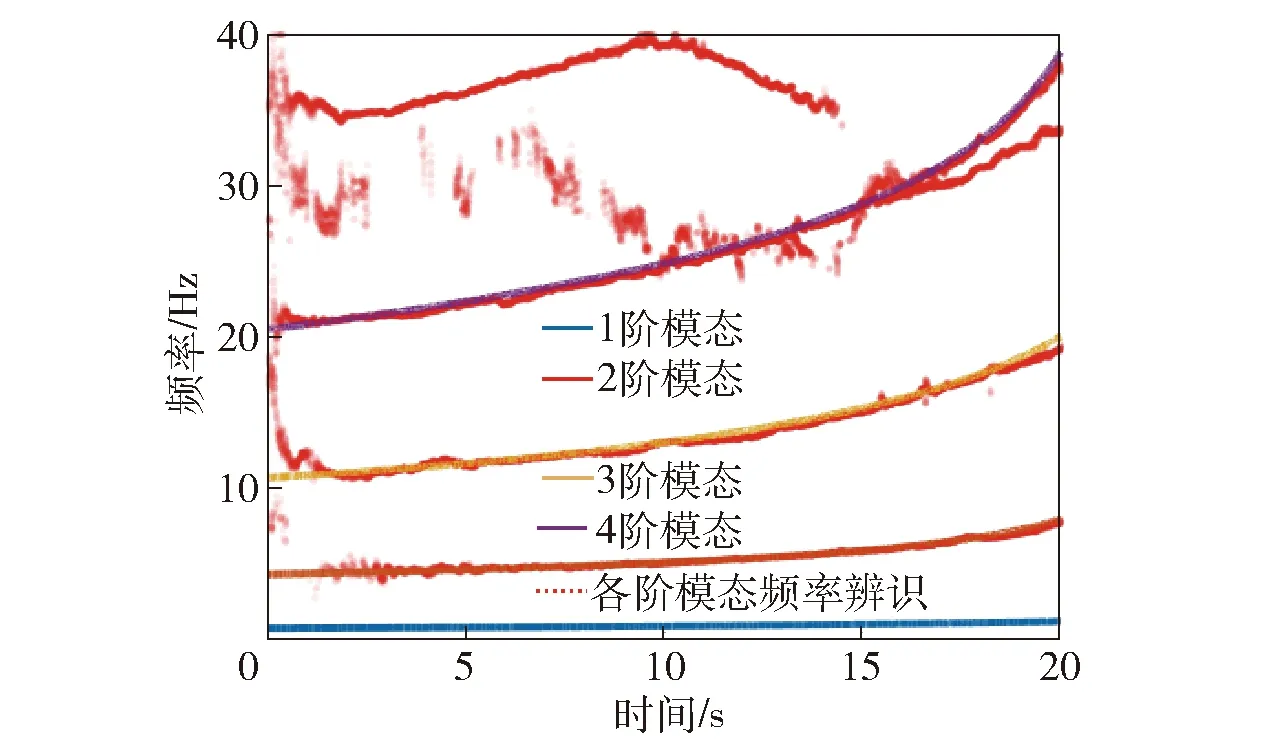
图8 递推小波基FS-TARMA模型冻结结构在不同 阶数模态频率的辨识结果Fig.8 Identified results of “frozen structure” modal frequencies with different orders using recursive wavelet basis FS-TARMA moclel

为了比较递推算法与批量算法的辨识效果，给出在相同模型结构下的小波基FS-TARMA辨识结果，如图9所示。

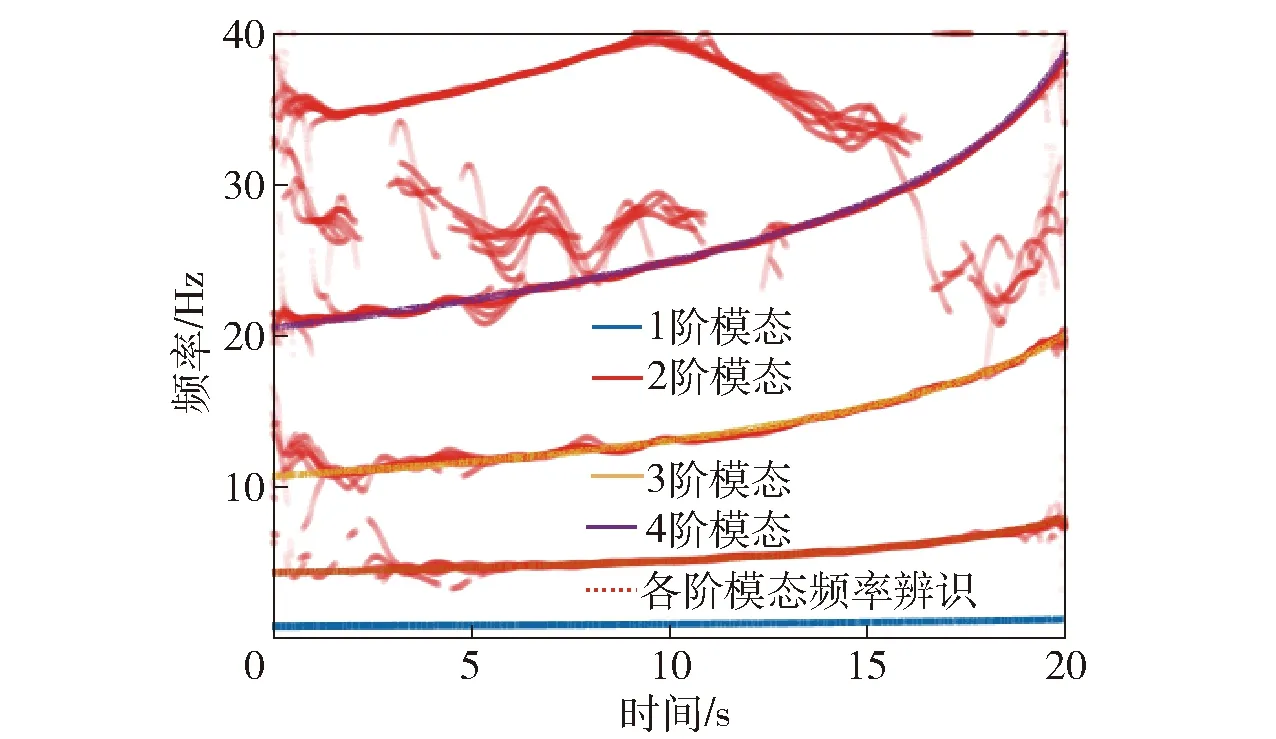
图9 小波基FS-TARMA模型冻结结构在不同阶数 模态频率的辨识结果Fig.9 Identified results of “frozen structure” modal frequencies with different orders using wavelet basis FS-TARMA model

由图8可知，本文所提的递推小波基FS-TARMA方法能够有效地识别时变系统的动态特征，在3阶模态频率上均能较好地跟踪系统的时变特征。通过图8和图9的对比可知：在辨识效果上，本文所提递推算法的虚假极点比非递推算法少，并且跟踪精度更高；在辨识精度上，二者在图中的差距并不明显，都体现出了良好的辨识精度。

为了定量比较不同方法的辨识精度与时变跟踪能力，定义均值绝对误差(MAE)[28]为

(29)

式中：f(t)为“冻结结构”模态频率值；l(t)为模态频率辨识值；L为数据长度。引入MAE计算方法，则两种方法的模态频率辨识结果的定量比较如表2所示。

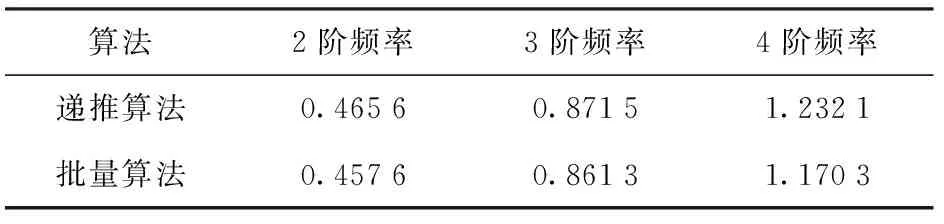
表2 固有频率估计误差Tab.2 MAE values for identification methods Hz

由表2可知，本文所提递推小波基FS-TARMA方法的辨识精度略低于批量算法，但是辨识精度上相当接近，3阶模态辨识频率最大相对误差在5%以内。为了进一步比较不同计算方法之间的计算效率，将估计过程所花费的CPU计算时间用于表征不同方法的计算效率，使用的计算机CPU主频为3.5 GHz，内存16 GB. 两种方法的计算时间如图10所示。

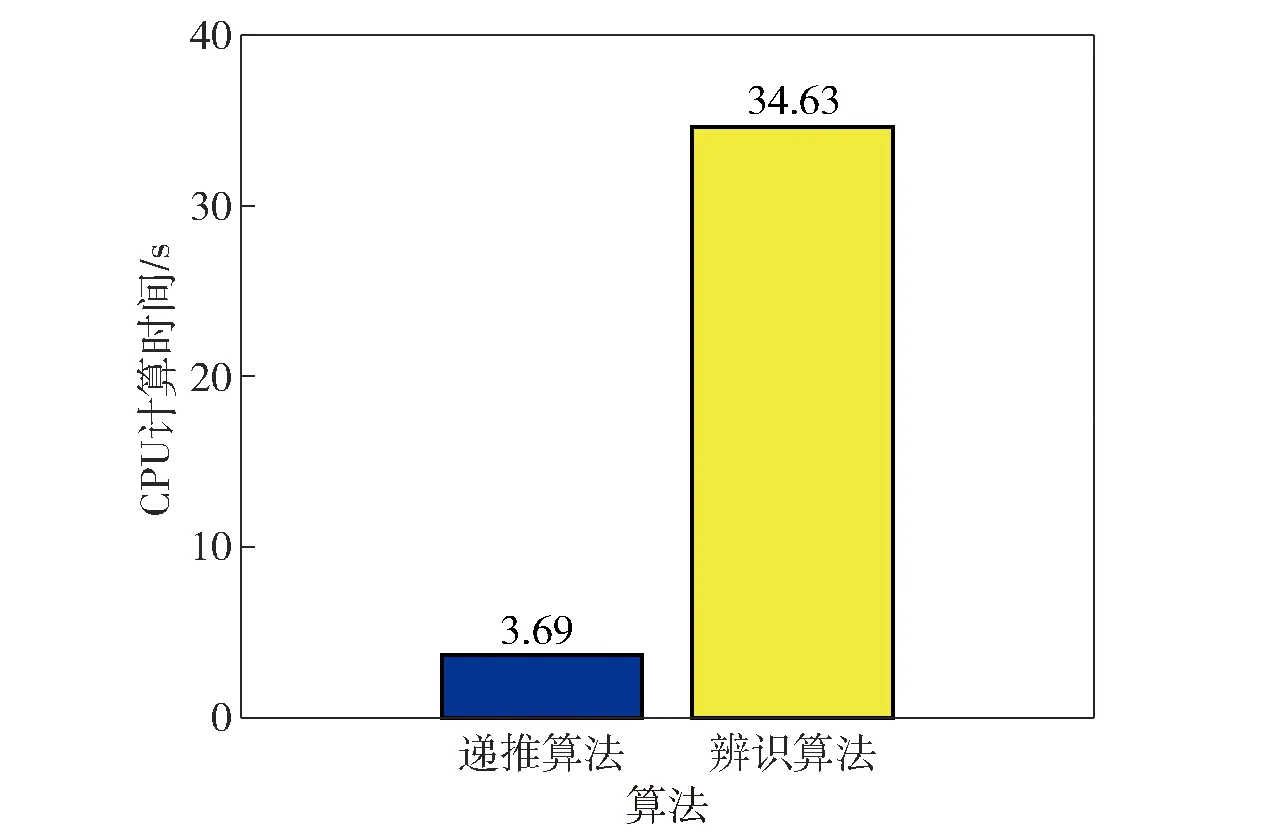
图10 CPU计算时间Fig.10 CPU computation time

由图10可知，在相同的时变系统、模型结构和计算条件下，本文所提递推算法计算效率与原方法相比，得到了较大的提升(提升约为9.38倍)。可见，本文所提算法具有更好的在线辨识能力，通过对结构化TARMA模型的递推化，不仅保留了结构化TARMA模型辨识精度高的优点，而且大大提升了其计算效率，为弹箭飞行模态的辨识提供了新的思路。

5 结论

针对弹箭在飞行状态下的时变模态参数辨识问题，本文基于FS-TARMA模型，利用小波基函数作为泛函基底构建时变参数矩阵，并借鉴于无结构化TARMA模型的递推思想，将投影参数矩阵视为数据长度的变量，提出了一种新的递推估计算法，实现了投影参数矩阵的递推估计。通过建立的阿里安Ⅴ号芯级运载火箭时变有限元模型，对所提辨识方法进行了验证，辨识结果表明：本文所提算法保留了批量算法辨识精度高的优点，同时大大提升了计算效率。