基于混沌集群智能优化算法的多目标粗糙集属性约减
2021-01-07李雪岩李学伟
李雪岩,李学伟,李 静
(1.北京联合大学 管理学院,北京 100101; 2.北京交通大学 经济管理学院,北京 100044)
0 引言
1982年,波兰数学家Pawlak发表了经典论文Rough Sets,标志着粗糙集理论的诞生[1]。自该理论诞生,粗糙集已在数据挖掘、模式识别、机器学习等领域与其他方法进行了广泛的结合,日益成为这些领域的重要方法;在应用方面,粗糙集在故障诊断[2]、生物医学[3]、风险评估[4]等领域也得到了广泛的应用。近年来,随着大数据与智能计算技术的不断发展,粗糙集的知识提取、特征选择等功能更加具有重要的理论及实践意义。
属性约减是粗糙集的重要计算模式,对于一个知识系统,属性约减就是在保持系统分辨能力不变的情况下,删去冗余数据,挖掘出关键属性。大数据背景下,各行业的管理活动会产生海量数据,但数据价值密度也随之降低,因此,通过属性约减技术删去冗余数据,发现关键特征,保持知识(数据)系统的分辨能力尤为重要[5]。
从优化问题的角度而言,搜索数据集的最优属性组合是典型的NP-Hard问题,智能优化算法常被用来求解此类问题,如传统的遗传算法[6]等。然而,知识系统之间具有数据结构、数据量、属性特征的差异,不同的算法也会产生寻优性能的差异,对于由复杂数据集构成的NP-Hard问题,智能算法的引入有效提升了属性约减的精确程度。
就管理实践中的问题而言,粗糙集中的决策属性体现了论域内研究对象在条件属性的作用下形成的产出或决策结果,大数据背景下,数据来源众多,相同的条件属性往往会在不同的决策情境下对应于不同的决策属性,这些在不同决策情景下形成的决策属性集合之间会产生差异甚至矛盾,对于相同的研究对象、不同的决策层次、决策场景也会产生不同的决策方案。在拓展粗糙集的决策属性分析维度方面,文献[7]基于区间值粗糙集理论,针对多个决策表设计了可以有效减小网络通信量的全局约减算法;文献[8]将测试成本和决策成本作为约简目标,提出基于特定类的多目标启发式属性约简算法;既有文献较多集中于求解高维数据条件下的全局属性约减问题,但对不同决策属性集之间的差异协调问题讨论较少。
由于单一决策属性的粗糙集约减问题可以转化为以属性重要程度为目标函数、以条件属性组合为变量的优化问题[9],因此本文对这一思想进行延伸,对多决策属性约减问题进行方法创新,将帕累托最优思想与多决策属性粗糙集约减问题进行有机结合,利用帕累托前沿描述不同决策属性之间的协调机制,形成离散多目标优化问题。对于离散多目标优化问题,在变量数目较多的情况下,一些传统的求解算法容易陷入局部最优或无法搜索到完整的帕累托前沿,因此需要引入合适的算法并对其进行相应改进[10,1]。近年来,随着多目标优化算法的不断成熟,越来越多的研究表明:具有群体交互机制的集群智能算法往往可以取得更好的优化效果[12,13];有效平衡算法的全局收敛性与种群多样性已成为提升计算性能的重要手段[14];在既有的尝试中,混沌算子的使用已被广泛证明可以用较小的计算代价换取算法搜索空间的增加,进而提升算法性能[15]。
综上,本文的工作可分为以下两步,首先依据管理实践及数据处理中的实际需求,将多决策属性粗糙集约减问题转化为离散多目标优化问题;第二,针对该问题的结构设计基于集群智能优化的求解算法及有效平衡全局收敛性与种群多样性的算子;最后,通过实际数据约减问题验证本文方法的有效性。
1 多决策属性粗糙集模型
1.1 粗糙集属性约减问题
依据粗糙集的基本原理,数据集合可以表示为一个知识表达系统:S=
定义1论域U中元素a等价的所有元素构成的集合[a]R={b∈U│aRb}称为a关于等价关系R的等价类。其中,R为论域乘积U×U={(a,b)│a,b∈U}的子集,aRb也可写为(a,b)∈R。
定义2K=(U,R)表示知识库,其中,R为U上的一族等价关系,如果P⊆R,且P≠Ø,则P中所有等价关系的交∩P也是U上的等价关系,这个关系叫做由P给出的不可区分关系,记作IND(P),对于知识库K,记IND(K)={IND(P)│Ø≠P⊆R}。
定义3给定知识库K=(U,R),则对于∀X⊆U和论域U上的一个等价关系R∈IND(K),子集X的下近似集与上近似集可分别表示为:

(1)

(2)

定义4知识的约减。设K=(U,R)为知识库,Q⊆P⊆R,R∈P。
(1)如果IND(P)=IND(P/{R} ),则称R在P中是不必要的;否则,称R在P中是必要的,P中所有必要的等价关系组成的集合称为P的核,记作CORE(P)。
(2)如果P中的每个等价关系在P中都是必要的,则P是独立的。
(3)如果Q是独立的,并且IND(Q)=IND(P),则Q为P的一个约减,P的所有约减组成的集合记作RED(P)。
对于由知识表达系统S=
(3)
(3)式表示决策属性对条件属性的依赖度;条件属性c相对于决策属性D的重要性程度可表示为:
SIGc=γC(D)-γC-c(D)
(4)
进一步,构成各个条件属性与决策属性的数据集可能会来源于多个领域,不同的条件属性与决策属性对论域中的对象都会形成基于等价关系的划分,而在同一个决策表中,仅基于等价关系的划分未必能够对不同的条件属性或决策属性产生有效识别,例如,令U={a,b,c,d,e,f,g},X={a,b,d,e,g},令R1与R2分别表示两种定义在U上的等价关系(R1与R2为条件属性或决策属性),假设R1与R2所产生的等价划分分别为U/R1={{a,b,d},{e,c,f,g} },U/R2={{a,b},{d},{e,c,f,g} },则X关于R1与R2的下近似集均为{a,b,d},依据(3)式可得R1与R2对应的属性重要性程度均为card[POSR1(X)]/card(U)=card[POSR2(X)]/card(U)=3/7。因此,(3)式的计算方式会产生属性重要性程度的计算误差。针对这一问题,本文引入知识分辨度的概念描述不同的等价关系[16]:
定义5令R为知识表达系统S中的等价关系,U/R={X1,X2,…,Xn},X1,X2,…,Xn表示等价类,则基于等价关系R的知识粒度可以表示为:
(5)
定义6令Reso(R)表示由等价关系R确定的知识分辨度,则有:
Reso(R)=1-Gran(R)
(6)

(7)

基于(4)式,条件属性c的重要性程度表示为:
(8)
可见,(7)式在(3)式的属性依赖度基础上同时考虑了等价类划分的差异,从而能够使等价关系对不同的条件属性产生有效识别。
1.2 多目标优化思想的引入
属性约减的目标是要找到约减后的条件属性组合{ci,cj,ck,…},使决策表在保持原有分类能力不变的前提下, 去除数据中的冗余信息。该问题可以表示为一个以知识依赖度为目标函数,以条件属性组合方式为变量的优化问题:
maxSIG{x1,…,xm},xi=0,1
(9)
其中,m为条件属性总数;xi为0-1变量,表示第i个条件属性是否为重要属性,SIG表示条件属性相对于决策属性的重要性程度。传统粗糙集决策表中,决策属性的设计大多较为单一,在现实的管理实践活动中,论域中的研究对象往往也会具有来自不同角度的多种决策输出(如不同部门的处理意见等),多种决策输出之间可能具有一定差异性,而这些决策输出又往往难以获得基于先验知识的数据支持,可见,具有多决策属性的粗糙集显然更加符合实际决策情景。因此,本文将多目标优化思想引入粗糙集属性约减方法,研究多决策属性条件下,关键条件属性挖掘的权衡问题。
多决策属性条件下,知识系统的决策表可以表示为:

表1 多决策属性知识系统
可见,针对每一个决策属性(d1…dn),都可以找到最优条件属性约减,将表1“拆分”为n个决策表,形成一个多目标优化问题:
(10)
多目标优化问题存在一组由众多最优解组成的集合,称为帕累托前沿。将(10)式转化为 (11)式,则关于粗糙集属性组合的帕累托前沿有以下定义:

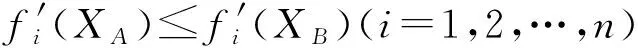
定义6非支配条件属性组合。如果属性组合XC∈S并且XC不被其他任何属性组合支配,则称XC为非支配条件属性组合。
定义7属性约减的帕累托前沿。由所有非支配条件属性组合计算得出的目标函数值集合在解空间中的表示称为属性约减的帕累托前沿(表示为PF)。

(12)
2 混沌集群智能属性约减算法设计
式(10)表示的属性约减问题是一个离散多变量多目标优化问题,相对于变量连续的优化问题,传统的求解算法容易出现陷入局部最优等缺陷。近年来,基于群体交互机制的进化算法被广泛证明具有较高的寻优效率,元胞遗传算法(Cellular Genetic Algorithm, CGA)在单目标优化及多目标优化中均展现出良好的性能[18]。针对上述属性约减问题的结构,本文对传统的元胞多目标优化算法(Cellular Genetic Algorithm for multi objective problems, MO-Cell)进行两方面的改进:(1)对每个种群中的个体建立非支配解集,平衡局部最优与全局最优的关系;(2)引入混沌算子生成初始种群、改进变异操作,提升种群多样性,形成新的多目标混沌元胞属性约减算法(Multi Objective Chaotic Cellular Attribute Reduction Algorithm, MOCCARA)。
算法步骤如下:
Step1种群初始化。本文采用三维元胞空间(N×N×N)进行种群初始化。三维元胞空间中,每个个体代表一组条件属性组合,每个个体具有上、下、左、右、前、后六个“邻居”(图1)。对于本文粗糙集中的m个条件属性、n个决策属性的约减问题,元胞空间内个体(i,j,k)的解可以表示为:
Xi,j,k=(xi,j,k,1,xi,j,k,2,…,xi,j,k,m),
其中,X∈{0,1}。

图1 三维元胞空间
其中,Xi,j,k中xi,j,k,l(l=1,2…m)取0或1的概率由混沌序列生成,本文采用遍历性较好的Cat混沌映射:
(13)
其中,xmod1=x-⎣x」。
Step2建立每个个体的非支配条件属性组合解集。令NDi,j,k表示种群中的每个个体(i,j,k)的非支配条件属性组合解集,依次将个体(i,j,k)每个“邻居”的条件属性组合及目标函数值加入NDi,j,k。加入规则如下:如果NDi,j,k中已有的条件属性组合被“邻居”的条件属性组合支配,则删去NDi,j,k中被支配的条件属性组合;如果“邻居”的条件属性组合不被任何NDi,j,k中已有的条件属性组合支配,则确认加入“邻居”的条件属性组合。
Step3建立全局非支配条件属性组合解集。令NDg表示全局非支配条件属性组合解集,将种群中所有个体的条件属性组合及目标函数值依次加入NDg。加入规则与Step2中向NDi,j,k中加入条件属性组合的规则相同,不再赘述。
Step4遗传操作。
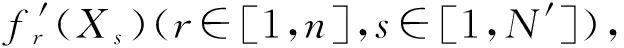

(3)交叉。设置交叉概率pc,依次对于Xi,j,k=(xi,j,k,1,xi,j,k,2,…,xi,j,k,m)中的每一个0-1变量xi,j,k,l(l=1,2…m),以概率pc变换为xi′,j′,k′,l,然后以概率pc变换为xi″,j″,k″,l。
(4)变异。设置个体变异概率pm,种群中依概率pm对交叉操作后的个体(i,j,k)进行变异操作,对于参加变异操作的Xi,j,k=(xi,j,k,1,xi,j,k,2,…,xi,j,k,m)中的每一个0-1变量xi,j,k,l(l=1,2…m),利用Cat混沌映射生成变异概率进行变异(0变为1,1变为0)。
经过上述遗传操作,元胞空间内每个个体的条件属性组合得到更新。
Step5返回Step 2。
Step6运行算法直到满足终止条件。
算法流程如图2所示。

图2 算法流程示意图
3 实际问题计算
测试案例:为了验证本文所提出约减方法的有效性,选取著名的UC Irvine Machine Learning Repository(http://archive.ics.uci.edu/ml/index.php)中的Turkiye Student Evaluation Data Set测试数据集作为测试案例对本文约减方法进行测试(选取前300个样本),该数据集中具有多个分类标签(如instr,class,attendance等),本文首先使用随机森林在不同的标签下对数据集进行训练,选取识别率最高的两个属性(标签)作为测试案例中的决策属性,构成两个不同的决策子系统。
此外,本文通过长期实地调研收集了若干铁路领域安全风险案例及处置方案的实际数据,并依据案例特点及实际操作对其进行编码,构建知识系统,形成本文计算案例。
实际计算案例1采用收集于某铁路局2013~2015年的设备安全风险处理数据构建风险处置决策表,条件属性为风险处置中所涉及的故障特征(共11种),选取两种重要的处理方案作为决策属性。
实际计算案例2采用收集于某铁路局2015年的设备安全风险处理数据构建风险处置决策表,条件属性为风险处置中所涉及的故障特征(共16种),选取两种重要的处理方案作为决策属性。
此外,算法参数设置如下:交叉概率pc=0.5;变异概率pm=0.05;元胞空间长度N=7。为了说明本文提出方法的可行性与有效性,本文同时引入传统的多目标优化算法NSGA-II与MO-cell进行属性约减,两种算法的种群数量均与本文算法相同,独立实验30次。
3.1 计算案例决策表
表2和表3给出了本文两个实际计算案例所构成决策表的字段简称。

表2 案例1安全风险处理决策表字段

表3 案例2安全风险处理决策表字段
3.2 计算结果分析
对于多目标优化中常用的经典测试函数,帕累托前沿的理论值往往比较容易获取,而对于基于实际问题的离散多目标优化问题,帕累托前沿的理论值往往无法获得,近年来,“支配率”与“超体积”(Hyper-volume,简写为HV)[15]常被很多学者用来衡量无法获取帕累托前沿理论值的多目标优化问题的优化结果,本文沿用这些指标。支配率与超体积的表达式分别用式(14)(15)表示:
(14)
(15)
其中,SCAB表示条件属性组合解集B中被解集A中的条件属性组合支配的百分比;Q表示帕累托前沿上最优解的个数,vi表示由前沿上第i个点与参照点形成的超体积,HV表示算法所获得的帕累托最优解集在目标域所覆盖的体积,HV值越大,帕累托最优解的质量越好。

图3 计算案例1条件属性重要性帕累托前沿

图4 计算案例2条件属性重要性帕累托前沿
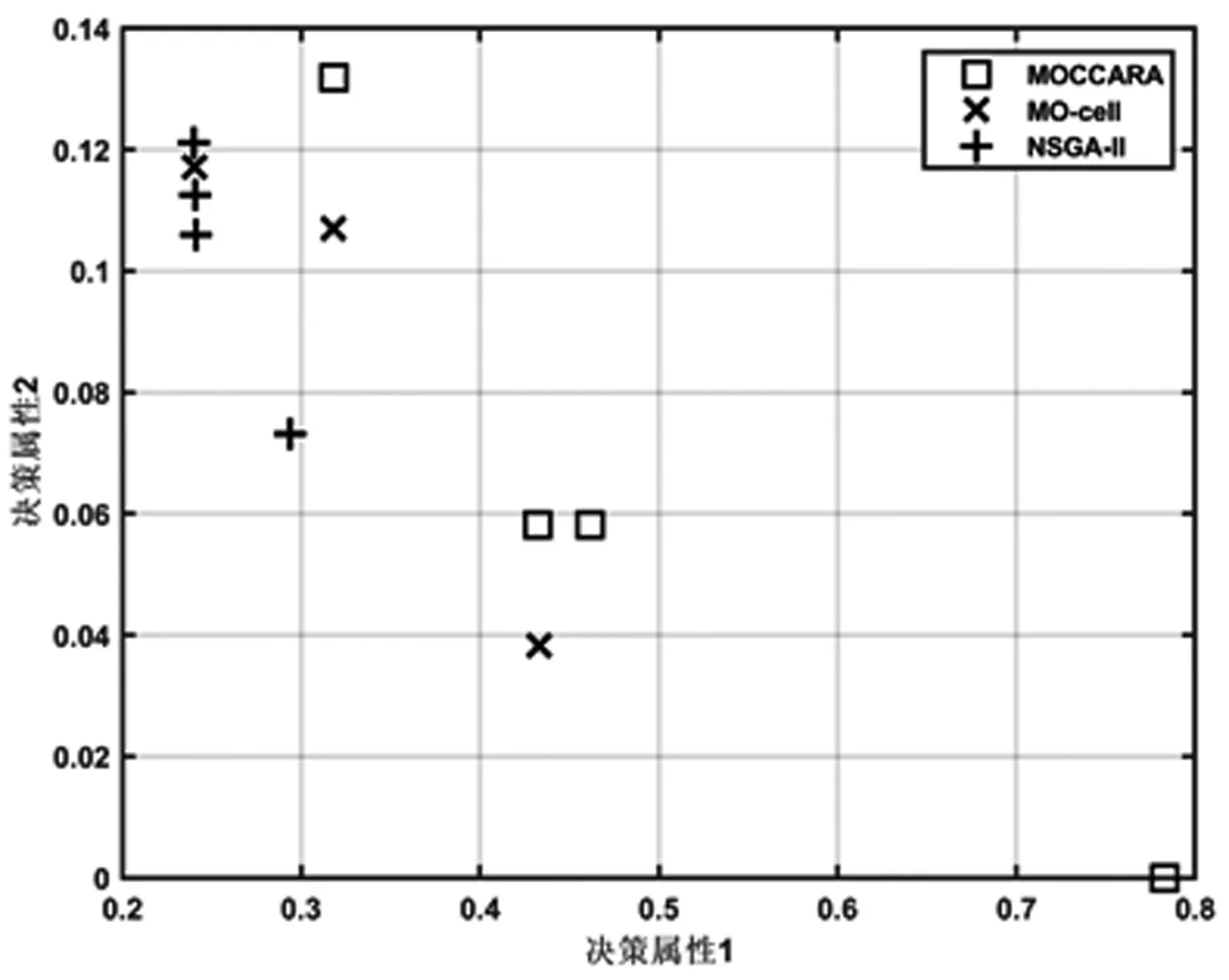
图5 UCI测试案例条件属性重要性帕累托前沿

图6 计算案例1所得解HV值统计

图7 计算案例2所得解HV值统计

图8 UCI测试案例所得解HV值统计

表4 不同方法约减效果对比(计算案例1)

表5 不同方法约减效果对比(计算案例2)

表6 不同方法约减效果对比(UCI数据库测试案例)
图3、4、5给出了三种算法在两个计算案例及一个测试案例中得到的具有代表性的粗糙集属性约减帕累托前沿,图6、7、8给出了不同算法所得到的最优解HV值的箱线图,由图6、7、8可见,对于计算案例1,MOCCARA与MO-cell算法获取了质量更好且更稳定的帕累托前沿;对于计算案例2,MOCCARA与NSGA-II算法获取了质量更好且更稳定的帕累托前沿。表4、5、6给出了三种算法在两个计算案例中的性能指标,对于计算案例1,由图3及表4可知,NSGA-II算法产生的帕累托最优解有13%被MO-cell算法及本文的MOCCARA算法支配且收敛时间更长,这说明本文的MOCCARA算法及MO-cell算法获取了更加理想的属性约减帕累托前沿;此外,虽然相对于MO-cell算法,本文的MOCCARA算法消耗了更多的运行时间,但也获取了更多的帕累托最优解。对于计算案例2,结合图4及表5可知,传统算法MO-cell产生的帕累托最优解中高达47%被NSGA-II算法及本文的MOCCARA算法支配,这说明本文的MOCCARA算法及NSGA-II算法获取了更加理想的属性约减帕累托前沿,虽然MO-cell算法的运行时间最短且获取的帕累托最优解个数相对较多,但得到的帕累托最优解以较大概率落入局部最优。此外,结合图5及表6可知,对于测试数据集,本文的MOCCARA算法虽然获取的帕累托最优解数量与其他两种算法相同,但最优解被支配的比例较少。比较图6、7、8可以发现本文的MOCCARA算法同时具有较好的稳定性。综上可知,MOCCARA算法取得了优异的属性约减性能。

表7 属性约减帕累托最优解集(计算案例1)

表8 属性约减帕累托最优解集(UCI计算案例2)
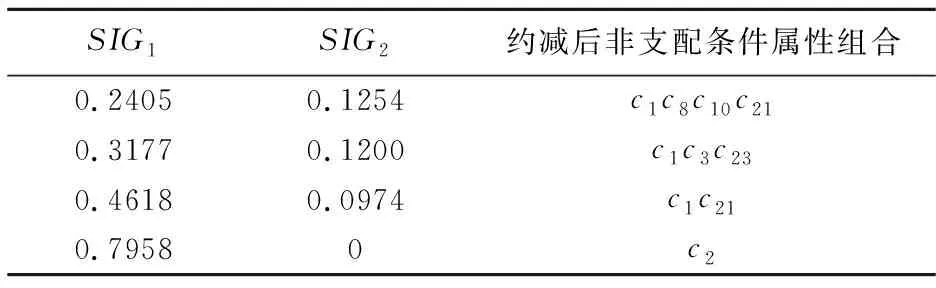
表9 属性约减帕累托最优解集(UCI数据库测试案例)
表7、8、9分别给出了两个计算案例获得的帕累托最优解集以及与每个最优解相对应的非支配条件属性组合。可见,随着最优条件属性组合在帕累托前沿上的位置变化(例如表7中的帕累托最优解(0.0411,0.0904)是倾向于决策属性2的约减),约减出的关键条件属性组合也发生了相应变化。这种现象在管理实践中有着较为重要的意义,以本文的计算案例为例,对于知识系统中的风险处置论域U={x1,x2,…,xK},不同的主管部门、领导层级、专业人员都会在决策过程中形成不同的处置方案(决策属性),即便是相同的风险,也会由于风险产生时的决策情境不同而产生不同的处置方案,这些方案之间难免会有矛盾之处,尤其是在大数据背景下,数据的属性、维度、层次众多,基于帕累托最优思想的引入为各个维度数据之间的全域联动与协调提供了一种新的处理机制,便于管理者挖掘不同维度数据之间的关系,实现不同数据维度下的科学决策,例如对于本文的安全风险处理知识系统,管理者可依据不同属性组合在不同处置方案条件下的重要性程度判别关键风险因素,提高风险因素挖掘的准确性。
进一步分析表7、8、9可知,现实数据条件下,虽然一组条件属性对一个决策属性的重要程度上升会使其对另一个决策属性的重要程度降低,但帕累托前沿在不同决策属性(目标函数)之间的分布(倾向性)并非均匀。例如表7中,条件属性对决策属性2的重要程度区间为[0.0702,0.0904],条件属性对决策属性1的重要程度区间为[0.0411,0.0702],小于前者。这一结果有助于管理者在缺乏先验知识的情况下首先判断决策方案变化所产生的条件属性组合重要性变化,进而为判别不同决策方案的差异提供了量化依据,然后以此为基础,依据条件属性对决策属性的重要程度区间挖掘关键条件属性。
4 结论
针对管理实践及大数据处理中的多维决策属性问题,本文将帕累托最优思想引入多决策属性粗糙集的约减问题中,将传统的粗糙集属性约减计算转化为离散多目标优化问题,实现了条件属性的约减在不同决策属性之间的协调。针对转化后的离散多目标优化问题,设计了基于元胞自动机的混沌集群智能算法并与传统多目标优化算法进行了比较,验证了本文提出方法的有效性。从方法设计的角度而言,本文针对所研究的问题获取了更为精确的帕累托最优解;从管理实践的角度而言,帕累托前沿思想的引入有效解决了如何在缺乏先验知识(概率)的条件下定量挖掘影响不同决策的关键条件属性(因素)问题,本研究的结果一方面可以帮助管理者增加属性约减的维度,实现不同数据维度下的科学决策及关键特征识别,同时也可以帮助其在属性约减过程中定量地实现不同决策角度之间的取舍与权衡。
本文采用的测试案例及计算案例均为确定性数据构成,而在现实中一些特定的决策场景中,用于特征提取的数据集会包含不确定性数据。因此,模糊集的引入则可以更好的解决本文模型引入不确定性计算的问题,此外,本文的研究没有考虑数据粒度、离散化程度等因素对决策结果的影响,这些都将在未来的研究中继续讨论。
