考虑等待提示策略的呼叫中心流体近似方法
2021-01-07孔凡文
于 淼,宫 俊,孔凡文
(1.沈阳建筑大学 管理学院,辽宁 沈阳 110168; 2.东北大学 信息科学与工程学院,辽宁 沈阳 110819)
0 引言
随着我国服务产业的深入发展,以呼叫中心为纽带的客户服务已经在各类企业运营中发挥重要作用,并且受到了越来越多企业的重视[1]。在高质量服务管理现实目标驱使下,排队等待提示作为新的运营模式被大多数呼叫中心所应用。“未知的等待相当于无尽的等待”,这种不可视队列的特点极大地降低了呼叫中心过程服务的顾客满意度[2],而排队等待提示正是克服了这种系统缺陷,使得呼叫中心通过语音提示的方式来改善用户的满意度。因此,如何充分考虑顾客行为的影响,有效地构造呼叫中心排队系统模型,进行等待时间预测及提醒已经成为管理者与学术界关注的焦点。
目前服务系统等待提示问题研究文献主要利用排队分析的手段,通过准确刻画带顾客放弃行为的等待提示排队系统服务流程,进行系统性能与效用的分析,从而为后续运营管理工作奠定基础。Armony等[3]研究了带有顾客回应的呼叫中心提示等待时间问题,并进行相应的均衡性分析。Jouini等[4]研究了带有提示可靠性选择的呼叫中心等待时间提示问题,详细考虑了等待提示信息对“直接退出”与“中途放弃”两类顾客行为的控制。Yu等[5]详细刻画了多种与等待提示有关的顾客满意度指标,从而进行有效的呼叫中心能力计划研究。Ibrahim等[6]以现实的大规模呼叫中心为背景,研究了考虑顾客回应的等待提示信息精确性问题。
除了以上排队系统中顾客放弃行为的刻画与分析,考虑顾客重拨行为影响的呼叫排队系统性能研究,亦是呼叫中心排队模型研究中的一类重要问题。由于考虑顾客重拨行为后的排队系统复杂性,使得利用传统的排队理论,兼顾构造系统多行为特征及求解系统性能变得更加地困难。近年来,一类确定型流体模型得到广泛应用,用以刻画顾客多行为模式下高负荷呼叫排队系统[7~9]。该方法避免了排队模型冗长的推导过程,利用确定型的流体表达简单且快速的获得排队系统的性能指标。Aguir等[10]最早通过流体近似方法构建考虑重拨行为的呼叫排队系统,并且通过与仿真模型的对比验证了近似的有效性。Ding等[11]利用利用流体近似方法进行带有重拨和重联行为的呼叫中心模型构造,并且进行了流体极限的证明。然而,目前还没有针对带等待提示的呼叫排队系统,考虑顾客重拨行为影响的相关研究。
为此,利用该确定型流体方法近似带有重拨行为的等待提示呼叫系统,丰富了文献[4]与文献[12]对于考虑顾客等待心理的提示等待呼叫系统,深入研究顾客提示更新行为基础上,构建更加符合现实呼叫中心多行为要素的呼叫排队系统,进行有效地等待时间预测以及性能分析。此外,基于离散事件调度法的仿真技术引用,有效地验证了该流体近似模型的精确性与实效性。该流体模型的构建为呼叫中心管理者对此类呼叫系统的合理管理与决策提供了有价值的参考策略。
1 问题描述及模型建立
1.1 问题描述
以带有等待时间提示机制的单技能多服务台呼叫中心为背景,系统具有s个服务台,排队规则为先到先服务(FCFS)。假设顾客首次到达过程服从参数为λ的泊松到达过程,且顾客接受服务过程服从参数为μ的指数分布,顾客打电话时具有初始的耐心等待时间T,其服从参数为γ的指数分布。排队服务流程如图1所示:

图1 带等待时间提示、直接退出、中途放弃,重拨的呼叫中心服务流程
令等待队列中的顾客数目为n。任意一个顾客到达时,如果系统中仍存在空闲服务人员,该顾客可以立即得到服务无需等待。否则,当n>0时,该顾客需要面临直接退出选择:“直接退出1”,为不接受任何等待的“极端不耐烦顾客”,选择退出的比率为α0,且放弃之后该部分顾客后续可能选择重拨,假设重拨服从参数为δ的指数分布,选择重拨比例为p;“直接退出2”,剩余顾客的行为选择根据等待时间的信息提示,当系统提示时间大于初始耐心时间,顾客选择“直接退出2”,pb(n)表示该部分退出概率,且pb(n)为系统通过近似提示时间可调节的概率。需要注意的是,假设“直接退出2”的顾客也将具有同样的比例p进行重拨,并且重拨过程同样服从参数为δ的指数分布。没有进行退出选择的顾客将接受提示信息进入队列进行等待。现实表明,选择进入队列的顾客将根据提示时间更新其初始耐心,令T′为更新后耐心时间,且近似服从参数为γ′的指数分布。如果更新耐心时间的顾客在等待之后,等待时间仍大于新耐心值而选择放弃则称为“中途放弃”行为。同样地假设中途放弃顾客以比例p进行重拨,重拨过程同样服从参数为δ的指数分布。
由于重拨行为的产生,使得系统总的被观测到达可以分为首次到达和重拨到达,令λ0表示被观测顾客到达率,假设两次到达过程相互独立。此外,令ρ为排队系统负荷(ρ=λ/sμ)。
1.2 等待时间提示策略
针对给定的呼叫中心排队场景,进行顾客等待时间的预测与提示策略设定。
定义1虚拟等待时间(Virtual waiting time)[13]:假设被提示等待信息的特定顾客有无穷大耐心时,近似得到队列中每位顾客的等待时间。
提示给顾客的等待时间根据虚拟等待时间D近似而得。其中,最终的实际等待时间与虚拟等待时间的偏差在于是否考虑的顾客耐心阈值,如果顾客在有限耐心时间内的等待时间则为实际等待时间,记作W,即顾客实际等待时间是虚拟等待时间与自身耐心时间比较后得到的结果,因此,
W=min{D,T′}
(1)
当系统的等待队列中的顾客数为n时,对于新到达的顾客,所近似的顾客虚拟等待时间为Dn和提示给顾客的等待时间为dn。此时,对于提示信息产生“直接退出2”概率pb(n),由于顾客初始耐心的指数分布特性以及提示时间dn,可得:
pb(n)=P(T (2) 不失一般性,当队列中具有个顾客n时,通过排队分析近似出顾客的虚拟等待时间Dn,并且按照某种提示策略确定近似的虚拟等待时间为Dn和提示等待时间dn之间的关联。具体地,由上文假设可知,留在队列的顾客耐心时间由初始的T变为T′,且γ′为“进入等待队列顾客”的中途放弃率。Dn作为更新后的耐心阈值γ′影响下的变量,表示当队列具有n个人等待时,新进入顾客欲获得服务之前需要等待的时间,不考虑输入过程,该顾客等待过程是纯灭的随机过程,如图2所示。Dn是从状态s+n+1到达吸收态s的等待时间,并且Dn的分布是参数为sμ,sμ+2γ′,…,sμ+nγ′的n+1个独立同指数分布的卷积,服从“亚指数分布”。 图2 系统纯灭过程示意图 令gn(t)表示变量Dn的概率密度函数,Gn(t)为Dn的累计分布函数,E(Dn)为Dn的期望值,因此有: (3) (4) 系统设定的提示策略:提示等待时间dn近似为虚拟等待时间Dn的平均值,即当一个顾客到达系统后,系统所公布的时间为前面n个等待顾客的平均等待时间,因此每位新到达顾客获得的提示时间随着队列的位置不同而变化: dn=E(Dn) (5) 因此,提示信息影响下的“直接退出2”概率可以改写成, pb(n)=P(T (6) 此外,在不同的呼叫系统中可能采取不同的提示策略,可以利用等待提示时间dn大于虚拟等待时间Dn的概率进行控制调节,即提示可靠性调节模型[14]: β=P(Dn (7) 该模型通过对β的整体控制用以完成对系统整体的提示时间策略,从而达到不同程度的缓解系统拥挤的目的。本文为了突出重拨行为的变化,设定的提示策略为平均等待时间,因此无需具体设置可靠性β的变化。给定提示策略后,接下来需要进行γ′的近似求解。 (8) 定义4队列中途放弃条件概率rθ(n):表示当等待队列存在n个顾客时,顾客在接受等待信息提示后,留在队列最后选择中途放弃的条件概率,可表示为: rθ(n)=P(T′ (9) 同时,由于T′的耐心系数权重表达,中途放弃概率可以写成: rθ(n)=P(θtk+(1-θ)dn (10) 进一步计算,得到 (11) 结合Dn的分布条件表达,rθ(n)可表达为 (12) 通过提示策略可以确定提示给每位顾客的等待时间表达式,然而当考虑顾客重拨行为时,此系统无法简单直接地获取稳态概率及性能指标。因此,接下来采用一类确定型流体近似方法,构造考虑顾客重拨影响的等待时间提示排队模型,并且求解相应的性能指标。 基于以上的等待时间提示策略,考虑顾客重拨影响因素,将以上随机模型进行简化近似处理,过程如下: 第一,利用连续型流体方法对考虑等待提示的排队模型进行近似,具体地,通过连续型状态空间表示相关随机排队模型,针对以上的排队分析可知,该系统可分为现实空间及虚拟的重拨轨道空间,因此该排队模型可利用二维空间模型表达。令向量(x1(t),x2(t))表示连续型状态空间的状态变量,x1(t)表示t(t≥0)时刻现实空间中系统的顾客数量,即正在服务的顾客与排队队列中的顾客数之和,x2(t)表示t(t≥0)时刻在虚拟的重拨轨道空间中顾客数量。结合首次到达与重拨到达,系统总观测到达率λ0为 λ0(t)=λ(t)+δx2(t) (13) 第二,利用行为分析表示该连续性空间流量变化,现实空间流量x1(t)的变化取决于顾客四类行为因素: “直接退出1”和“直接退出2”,中途放弃及获取服务。首先,直接退出的行为因素包括极端不耐烦顾客及等待提示导致的退出顾客,减去直接退出的顾客,x1(t)的实际进入流量为(1-α0)(1-pb(x1(t)-s))λ0(t),其中,α0表示t(t≥0)时刻现实空间中根据极端不耐烦顾客的概率,也就是系统顾客数为x1(t)时的“直接退出1”概率;pb(x1(t)-s)表示t(t≥0)时刻现实空间中根据等待提示放弃的概率,即当系统顾客数x1(t)为时的“直接退出2”概率。 中途放弃行为导致的x1(t)的流出率,利用式(12)的中途放弃条件概率的计算方法,可得当t(t≥0)时刻系统顾客数为x1(t)时,中途放弃的条件概率为rθ(x1(t)-s),此时中途放弃行为导致的流出量x1(t)为(1-α0)(1-pb(x1(t)-s))rθ(x1(t)-s)λ0(t)。值得注意的是,还可以根据顾客更新耐心时为指数分布的假设,表达另一种中途放弃行为导致的x1(t)流出量为γ′max(x1(t)-s,0),因此可得: γ′max(x1(t)-s,0) =(1-α0)(1-pbx1(t)-s))rθ(x1(t)-s)λ0(t) (14) 获得服务行为导致的x1(t)的流出率,可以写作μmax(x1(t),s)。 第三,考虑稳态条件下,系统的状态空间表达。首先,现实空间缓冲区中顾客数x1(t)的总变化率如下: γ′max(x1(t)-s,0)-μmax(x1(t),s) (15) 在虚拟轨道空间上,顾客数x2(t)的增加来源于直接退出和中途放弃两类行为,该轨道空间流量的减少来源于重拨行为的发生,因此有 γ′max(x1(t)-s,0))-δx2(t) (16) 当排队系统达稳定状态时,满足条件 (17) 因此,可得稳态下两个状态变量趋于常数 (18) 当系统低负荷的场景下ρ≤1时,虚拟轨道空间上的顾客流量数x2(t)稳定状态时水平为0,此时流体近似方法提供的系统重拨率信息误差较大。因此,重点考察超负荷ρ>1场景时系统状态的变化过程,此时系统稳态条件下满足x1≥s,并且max(x1-s,0)=x1-s与min(x1,s)=s。由以上条件可以构造以(γ′,x1,x2)为向量解的方程组, (19) 对应地,式(19)中“直接退出2”概率pb(x1-s)与“中途放弃”条件概率rθ(x1-s)分别通过式(2)与式(12)的未知量γ′进行计算,并利用式(13)获取被观测到达率λ0。由此,该排队系统的性能指标可以根据求解式(19)中三维向量(γ′,x1,x2)获得。 针对流体近似方法建立的呼叫排队模型,设计一类蒙特卡洛计算方法[15]求解式(19)中向量解(γ′,x1,x2),从而获取系统的相应性能指标。具体地,f为表示式(19)的方程组函数,y为解向量。算法的主要步骤如下: 步骤1参数初始化i=0,令最大搜索步数为N,步长向量h,并且初始解为y0,其中h=(h1,h2,h3),y0=(y00,y01,y03)T。并计算 F(0)=f(y0) (20) 步骤2更新i=i+1。如果,则h=h/2,i=0。 步骤3生成正态分布的随机向量y1,其中,y1~N(y0,Σ),Σ=diag(h1,h2,h3)。并且计算 F(1)=f(y1+h) (21) 步骤4如果F(1)≥F(0),则转回步骤2;否则进入步骤5。 步骤5如果|F(1)|≤ε,则y1是式(20)的解;否则,令y0=y1,然后返回步骤2。 由此可以利用(γ′,x1,x2),求解稳态条件下基于流体近似方法的呼叫排队模型所有性能指标。具体地,选取顾客直接退出的概率PB,顾客中途放弃的概率PR,顾客获得服务的概率PS,同时包含考虑重拨行为因素下,直接退出和中途放弃后共同生成的稳态重拨率Tr, PB=α0+(1-α0)pb(x1-s), (22) 通过分别与传统的解析方法与仿真方法两种不同的构造方法对比,共同验证等待提示排队系统中流体近似方法的有效性与精确性。首先,针对等待提示机制影响下的排队模型,不考虑顾客重拨行为前提下,通过流体近似方法与传统的马尔科夫方法两类方法的对比分析,验证流体方法对此类高负荷排队系统近似的有效性;其次,针对1.3节中的考虑等待提示机制及顾客重拨的排队模型,由于该模型的高度复杂性,目前没有解析方法的相关成果研究,仅能进行流体近似方法与仿真方法建立的排队提示模型对比,从而验证复杂排队系统的近似有效性。其中,流体近似模型与解析模型采用Matlab实现,仿真模型采用C++实现,在Microsoft Visual Studio 2018 开发环境下运行。所有数值实验在Intel(R),Core(TM)i7-520M CPU,2.9GHz,4.00GB内存的计算机上进行。 参照文献[4]提出的考虑等待提示的排队模型,该模型利用马尔可夫近似的方法进行等待提示时间预测,并且求解相应的系统性能。首先针对无重拨行为的等待提示排队系统,对比文献[4]的解析方法进行验证分析。同样地,通过流体近似方法构造该等待提示系统,排队系统状态变量仅含t(t≥0)时刻现实空间中顾客数量x1(t),由于无重拨行为,此时顾客首次到达率λ即为被观测到达率。参照式(19)构造方法,可得以(γ′,x1)为向量解的系统方程: (23) 同样地通过蒙特卡洛算法求解式(23),可以获得无顾客重拨的等待提示系统的性能指标PB与PR。接下来,在该无重拨的等待提示排队模型中,利用流体近似方法与马尔可夫近似方法[4]求解的直接退出概率PB及中途放弃概率PR比较,进而验证流体方法对该排队系统近似的有效性。为了验证近似方法的性能指标差值,定义顾客直接退出及中途放弃两类行为相对误差值,例如顾客直接退出概率的相对误差值为|PB(流体)-PB(随机)|/PB(随机)。选取系统参数μ=1,γ=0.8,θ=0.1,α0=0.05,以下无特殊说明则相关参数设置不变。 首先,固定系统的人力资源配置水平s=20,如表1所示,通过顾客首次到达率λ的变化从而变换系统负荷ρ的值,分别获取两类方法的放弃行为指标的相对误差结果。随着ρ逐渐增大,流体近似方法的相对误差值大幅降低,说明流体方法的精度随着系统负荷增加而增加,直至趋于解析方法的结果,符合对流体近似方法的变化原理预期。此外,直接退出的近似效果明显好于中途放弃的近似效果,原因可能是由于两类方法的“中途放弃”行为均需要中途放弃率γ′的双层近似,两部分近似叠加而从而导致两类方法的不精确性,误差值增加。 表1 无重拨行为的等待提示系统的性能比较s=20 其次,固定ρ=150%,如表2所示,考察人力资源配置水平s不断增加下,系统规模增大导致流体方法的近似精度变化。当s逐渐增大,两类方法的性能指标误差值逐渐降低,说明在该场景下流体近似方法的精度随着s的增加而增加。与表1的对比下,s变化导致的误差变化幅度明显小于系统负荷产生的作用幅度,综合两表说明系统负荷是影响流体方法近似效果的关键因素,并且大规模呼叫中心同时系统负荷较大时,流体方法具有较好的近似效果。 表2 无重拨行为的等待提示系统的性能比较ρ=1.5 考虑顾客重拨行为时,由于传统的随机方法[4]无法进行近似求解系统性能,利用仿真方法构建等待提示排队模型,用以对照1.3节所提出的流体近似方法模型下的系统指标,从而验证确定型流体方法的近似质量。具体地,流体方法利用蒙特卡洛算法求解式(19),从而获得模型的相关性能。仿真模型采用的是离散事件仿真技术[16],即利用事件的变化描述系统状态随时间的推进。该仿真模型为稳态仿真,利用重复删除法,仿真结果采用500次重复仿真所取均值。 首先,考察两种方法下,重拨率的相对误差结果。如表3所示,选取p=0.5与δ=0.5,固定系统的人力资源配置水平s=20,通过顾客首次到达率λ的变化从而变换系统负荷ρ的值,从而观察流体方法与仿真模型两类方法获取的Tr误差结果。与传统马尔科夫方法对比结论相同,当ρ=100%时,流体近似方法误差较大,误差率达到100%,而随着系统负荷增加,流体方法的近似精度逐渐提高直至趋于精确的结果,符合1.3节中的假设分析。 表3 考虑重拨行为的仿真方法与流体方法性能比较s=20 其次,选取p=0.5,当重拨返回时间分布率δ=0.2,δ=0.5,δ=0.8三种情况时,流体方法的近似相对误差变化规律。如图3所示,随着ρ逐渐增大,不同重拨返回时间分布率下的重拨率Tr相对误差值全部降低,直到趋近0,说明流体方法的精度随着系统负荷增加而增加,与之前的对比变化趋势相同。并且随着重拨返回时间分布率的值越大,近似精度相对更高。因此,增加考虑重拨行为的背景下,通过与仿真方法的对比分析,验证了流体方法对复杂系统近似应用的有效性。 图3 确定型流体近似方法的顾客重拨率相对误差值 本研究通过一类确定型的流体近似方法,克服排队系统复杂的背景建模要素,针对等待信息提示的呼叫中心的服务系统,从排队心理学角度出发,考虑等待过程中的顾客耐心变化,以及顾客放弃与重拨行为的特点,突破性地对该模式下的呼叫系统进行构造及分析,并提出了基于蒙特卡洛法的模型求解算法。通过流体模型与两类模型的比较分析,包括“传统马尔科夫”的解析模型与“离散事件技术”的仿真模型,得出如下结论:无论是否考虑顾客重拨行为的等待提示排队系统,对于大规模呼叫中心同时系统负荷较大时,流体近似方法的性能误差值较小,即该结果表明流体方法近似效果较好。总之,研究结果显示流体方法的模型表达可以快速且有效地获得等待提示影响下排队系统性能,对于考虑等待时间提示的呼叫系统运营具有重要指导作用。



1.3 基于流体方法的提示排队模型近似
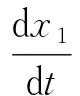
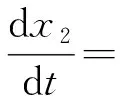
1.4 基于流体方法的呼叫排队模型求解
PR=(1-α0)(1-pb(x1-s))rθ(x1-s),
PS=1-PR-PB,Tr=δx22 近似模型验证及结果分析
2.1 基于马尔科夫方法的等待提示模型验证分析

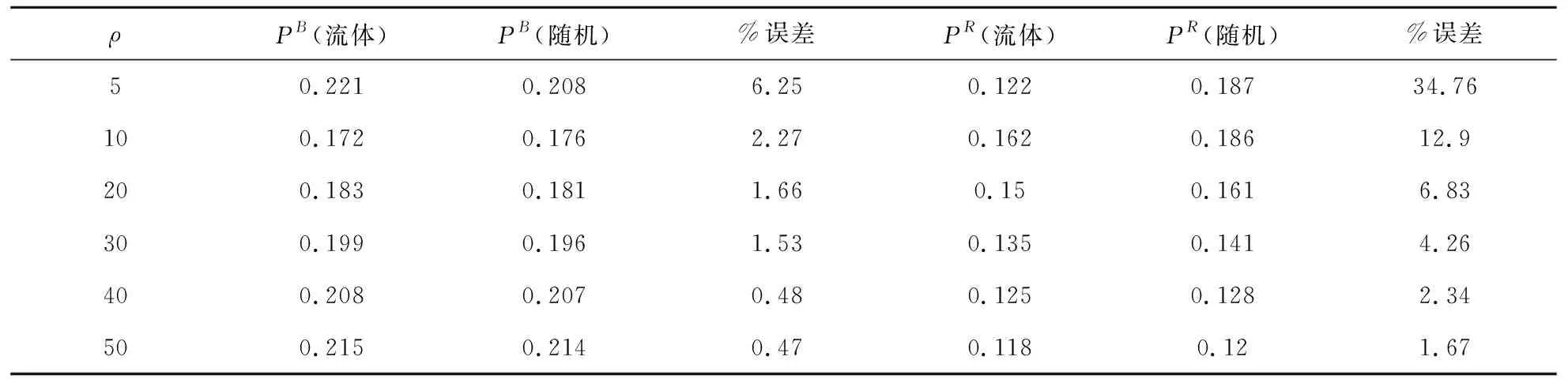
2.2 基于仿真方法的近似排队模型验证分析


3 结论
