区域集群下板材订单配置模型及算法研究

孙卫红，吕文新

(中国计量大学 机电工程学院，浙江 杭州 310018)

0 引言

为了适应经济发展的大潮流，在某一地域范围内的中小型企业联合协作，逐渐形成了以一个主导产业为核心的企业集群[1]。

板材资源作为集群企业常见的物理资源，批量大，库存多，同类配套企业数量多，当某一企业出现缺料情况时，集群的地理空间优势可以帮助企业需求方实现快速补充。然而在现实情况中，由于板材资源空间分布的不均衡、企业之间缺乏及时有效的信息交互，往往导致集群企业间未能进行有效的协作和资源共享，无法发挥出集群的区域整体优势[2]。

利用网络和云制造服务平台，为集群企业的资源进行聚合、共享、管理和调度提供了一个非常好的解决思路，但是由于平台资源量巨大，需求与供应之间是往往是多对多的匹配问题[3]，人工方法耗时耗力，需要通过调度算法实现平台供需的智能匹配。

郝春亮等就固定的集群资源条件下，对内部资源的快速获取提出了四种调度结构[4]；方伯芃等针对产业链内部资源，对产业链生产与配送的协同调度优化问题进行建模，并通过启发式寻优求解得到最优方案[5]；徐小峰等针对带时间窗和资源约束的资源集成调配问题，构造了网络任与资源的集成调配模型，并采用遗传算法对模型进行求解[6]；陈友玲等从能力资源角度出发，根据不同需求订单的效率值，为资源供应方选择对应的需求方[7]；王静等通过订单拆分数和订单最小分解率两个变量对云平台下订单生产计划进行调节,并设计双层编码、运用自适应模拟退火遗传算法对不同数据规模下的模型进行求解[8]；颜波等提出了离散型帝国竞争算法对订单调度流程进行求解,以处理大批量复合订单问题[9]；白小振等针对钢材企业的板材资源提出了基于遗传算法的无委托板坯合同优化[10]；呼万哲等设计了一种以最小化订单余材为目标的结合禁忌搜索和列生成技术的混合优化算法[11]；王晓欢根据不同订单的利润水平提出了基于强化学习的企业订单接受策略[12]。上述方法从产业优化、减少库存、获取利润等角度提出了多种解决资源调度的模型算法，旨在以资源供应商的利益构建订单匹配模型，缺少从资源需求方的角度考虑资源的调度问题，而且在利用区域集群的地理优势上也相对欠缺。

本文中，将区域网络化板材制造资源的共享与配置，分为服务平台匹配和物流空间运输两部分。以资源需求方的利益为主，着重考虑了订单匹配成本和物流成本等因素，构建区域板材资源共享平台，解决集群企业板材资源调度问题，加深企业间的资源共享和网络联盟，降低产品制造成本。

1 集群资源特征与系统结构控制

1.1 区域集群资源特征

区域集群的板材和企业通常具有以下几个特征：

多样性和确定性[13]：板材资源种类、规格、质量标准等要素繁多，区域内总资源数量庞大丰富。

产业一致：集群企业的产业关联程度强，形成的核心产业簇群的资源基本相似，资源可获得性高。

分布相对集中：各企业地理位置分布不同，但往往集中在某个区域内，交通相对便利，有良好的合作基础和区域优势。

1.2 系统配置结构设计

企业板材资源需求与供应匹配具体流程如图1所示。板材资源的需求方将板材需求分解为子订单上传至共享平台，根据子订单中板材的种类、规格标准等物理要求进行基本分组。板材供应方对板材属性按照模板参考分解后，做统一的规范指标和描述，虚拟化处理后上传至资源共享池，为接下来的匹配工作缩短匹配时间和提高匹配精度，让其具有更好的针对性和适应性。然后根据调度模型匹配出具有合适的供应商，最后完成子订单的配送。

图1 板材订单匹配流程

2 匹配要求及约束模型

对于集群企业来说，板材的采购与供应基本上已经建立起了长期互信的伙伴关系，这也是集群发展的重要基础。因此，板材采购的成本控制成为了影响需求方企业经济利益的一个重要指标。降低采购成本，是需求方企业在采购过程中最重要的考虑因素之一。

平台上有多个板材资源申请请求，每个请求可以分解为多个子订单。各子订单在板材规格、型号等属性方面约束不再讨论。根据客户要求，本文建立了一个以资源需求企业采购总费用最低为目标的优化模型，来指导平台将子订单分配给合适的集群供应商。

2.1 符号定义

模型中参数或变量符号定义：

(1)订单表示

i为订单分解后的子订单序号，共Qm个；

ωi为子订单i所需要的订单量；

Porder为订单的预算成本，包括所有订单的采购成本与运输成本。

(2)供应商表示

j为平台上针对子订单i的供应商序号，共Ni个；

pij为企业编号是j的供应商对i子订单提出的货物单价；

dij为子订单i的需求方与供应商的距离；

ωij为供应商的库存量；

tcon为该区域每单位订单量在单位运距下的运输成本。

(3)决策变量

Zij为0-1变量，若子订单分配给供应商j，则为1，否则为0。

2.2 资源配置目标函数

分解后的子订单费用可以分为两部分，分别是用户购买物料资源的花费成本和物料的物流运输成本。

以子订单分配的供应商给出的单位参考价格为标准，计算出每个子订单对应板材需求量的材料采购成本。订单用于购买材料的花费为C1所有子订单采购成本之和，其表达式如下：

由于区域企业集群各企业间具有良好的交通优势，在同等情况下，应该优先考虑距离板材需求方更近的供应商，同时也可以降低运输成本。各个子订单材料物流运输总费用之和C2可以表示为:

综上所述，平台上一个订单总费用之和C可以表示为:

2.3 约束条件

根据模型，可以建立模型的约束条件如下:

dij≤s,i∈Om,j∈Ni

(1)

(2)

ωi≤ωij,i∈Om,j∈Ni

(3)

C≤Porder

(4)

dij>0

(5)

其中：约束(1)为距离约束，表示物料需求企业和物料供应企业之间具有距离限制，要求物料需求企业与物料供应企业在同一个企业集群中，确保两者在可配送范围内。s为该物料需求企业距离物流供应企业的距离上限；约束(2)为供应商选择约束，确保订单i提出的需求只能由一个企业供应商供应，避免多家物料供应企业重复接同一子订单；约束(3)为供应库存约束，要求物料供应企业的物料库存可以满足订单i的物料需求量，ωij为物料供应企业的物料库存；约束(4)为成本约束，要求订单分配后的总成本在用户给出的成本范围之内；约束(5)为自然约束，避免不符合常规的约束。

3 IA-PSO混合算法实现订单配置

PSO算法具有结构简单、运行速度快的优点，但是该算法却也往往有搜索精度不高，容易陷入局部最优，出现早熟收敛等缺陷[14]。如果在进化探索阶段，能够保持其种群的多样性，就能大大避免算法出现早熟收敛的现象。

本文提出的IA-PSO算法，将人工免疫算法与粒子群优化算法相结合，在保留了交叉、变异等固有遗传操作的基础上，借助免疫记忆特性和克隆选择等粒子群算法所欠缺的机理，根据抗体适应度将抗体群划分为支配解与非支配解，对其进行促进或抑制作用。这样不仅提高了算法的全局搜索能力，达到避免早熟收敛的目的，而且算法对个体的评价也更加全面，个体选择方式也更为合理，保证了解的多样性。其算法流程图如图2所示。

图2 算法流程图

3.1 基因编码

在可行解空间随机产生初始数量为的抗体群。如图3所示，免疫系统是由基因长度为M的N个抗体组成，抗体基因编码需要考虑每一位对应基因的顺序。设抗体ai为一个可行的订单分配方案，ai=[ai1,ai2,…,ain],其中，i∈{1,2,…,N}是订单编号，aij∈{1,2,…,n}表示第i个订单中的子订单j所分配的供应商企业编号。例如一个订单分配的可行解为[2,7,15,21,19]，它代表该订单分解后的子订单1、2、3、4、5分别分配到编号为2,7,15,21,19的企业供应商上。

图3 抗体基因表示

3.2 交叉操作

由于单点交叉交换基因量大，容易破坏优秀个体，因此交叉操作采用双点交叉法，操作方法如图4所示，结合来自父代交配种群中的信息，随机确定两个不同的交叉位置，将切点中间位置信息作为交换对象，产生新的个体。

图4 双切点交叉操作

3.3 免疫克隆操作

由于免疫算法在抑制高浓度个体时，与抗原亲和度最高的个体也会受到抑制，这样很可能会导致已经求得的最优解丢失。为了防止这种情况发生，采用精英保留策略，先将与抗原亲和度按降序排列取前N/2个体存入记忆库，剩余群体按照期望繁殖概率选择优秀个体存入记忆库。

为了在剩余抗体群中选择出更优的个体，本文提出了一种惩罚制度，通过比较适应值结果与用户给出的订单预期成本，将剩余抗体种群划分为支配解和非支配解。当订单分配后的方案总费用高于用户预期，定义其抗体种群为非支配解，给予抗体抗原亲和度值一个费用违反惩罚。

设计非支配解其抗体与抗原之间的亲和力函数Av如下：

其中，F(xi)为该抗体得到的订单分配方案所生成的总费用，xi为抗体对应基因位上每个子订单分配给供应商的解。

定义剩余抗体被选择的概率可以表示为:

其中，α为常数。根据上式可以得到，当费用过高的时候，抗体被选择的概率会降低，抗体上每个基因位对应的解即为每个订单对应分配企业的编号，从而获取每个订单解。这保证了高适应度个体的繁殖，同时又确保了个体多样性。

4 实例应用与结果

为验证模型和算法的有效性，以浙江某木制玩具企业集群为背景，对模型进行试验与分析。构建一个用于管理企业板材资源的信息平台，选取部分企业用户实际订单需求与企业愿意承担的订单预期成本作为参考，通过信息平台发布为板材需求订单，分解为子订单后上传至信息管理平台，供应商企业通过上传自身板材资源库存信息将区域分散的板材资源进行整合,经过匹配后为用户的不同子订单选择出价格最低的供应商企业作为参考。

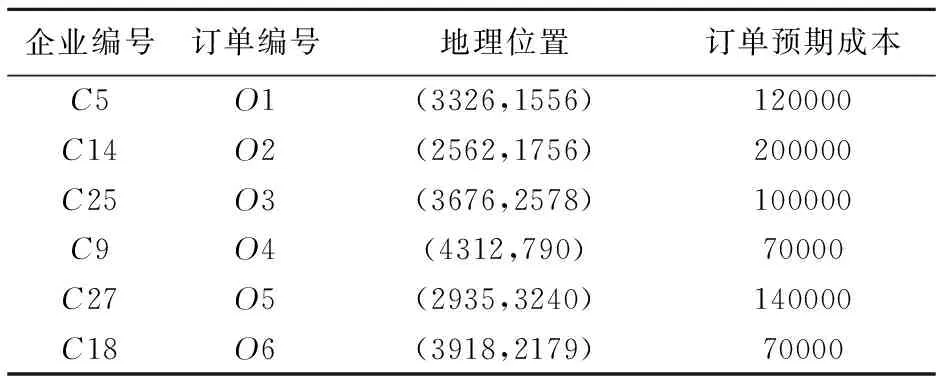
表1 申请资源发布订单

表2 订单分解

平台上有六个企业用户发布了订单与订单预期成本，如表1所示。每个订单经过分解后，对应为如表2所示的相应子订单。平台上对应的供应商及其提供的板材资源如表3所示。

表3 平台板材资源供应

表4 子订单分配方案

根据调度模型及算法，使用MATLAB对订单分配模型进行编程求解。为了测试算法的实用性，在给出相同实验条件下，采用粒子群算法作为对比实验。

IA-PSO算法初始化参数如下：迭代次数为100，种群规模为50，记忆库容量为10，交叉概率为0.5，变异概率为0.4，多样性评价参数设为0.95，抗体亲和度阈值取0.7。经过算法匹配，各订单的分配方案如表4所示。以编号为1的订单为例，订单1经过处理后被分解为6个子订单，通过运算配置，子订单依次被分配给编号为23、4、16、7、6、2的供应商企业，并给出了每一个子订单的成本费用，订单1的总费用为109900元，低于用户给出的订单预期成本，说明该算法对于集群内订单的分配具有一定指导意义。

同时，IA-PSO混合算法与传统PSO算法相比较，算法最优解的变化曲线如图5所示，传统PSO算法在迭代50次左右陷入了局部最优，并最终收敛于最优解582960，IA-PSO混合算法收敛于其最优值554125，证明了IA-PSO算法明显具有更好的全局搜索能力，改进后算法的费用节省了全部订单费用的5.2%。

图6展示了板材订单资源的供应方与需求方在集群地理位置上空间分布。排除库存量不足的供应商，订单的分配几乎均选择了距离用户的较近范围内的供应商，不但缩短了板材运送时间，同时也节省了相关的物流运输费用。

图5 算法最优解变化曲线

图6 订单分配企业地理位置示意图

5 结论

针对区域企业集群中板材资源特点，综合考虑区域集群中企业用户资源库存和区域物流的空间等因素，着重参考了集群内企业分布、订单分配总费用最小化等需求，构建了区域内企业集群板材订单分配数学模型，并提出IA-PSO混合算法对其进行求解计算，使整个订单分配收敛于全局最优解。最后以某木玩集群板材订单匹配为例进行试验验证，结果证明该算法能够得到更优的订单分配方案，有效解决了区域集群内板材订单的分配问题。