利用K均值聚类算法识别遗传疾病致病SNP位点

张恒益，郑惠玲

(西北农林科技大学 动物科技学院,陕西 杨陵712100)

生物医学研究表明，许多疾病都有相应的致病基因或易感基因。复杂疾病往往由基因变异引起，但致病基因的精确定位却不易做到[1-2]。在组成DNA的碱基对中，一些特定位置的单核苷酸发生变异引起的DNA多态性称为SNP (Single Nucleotide Polymorphism)位点。SNP是最常见的基因变异类型，识别致病SNP位点对精确定位致病基因具有重要意义。Pico等[3]通过识别致病SNP位点找到了孟德尔疾病的缺陷基因；Irina等[4]发现了克罗恩(Crohn)疾病相关的致病位点；Pernille等[5]发现了一些与情感信号传导障碍相关的SNP位点。牛蜘蛛腿综合征是一种以骨骼畸形为病理特征的先天致死性遗传病，该病有两个致病位点[6]。另外还有许多家畜遗传疾病是由致病位点或基因引起，如肢蹄畸形、血友病、鸡的卷羽、猪的应激综合征等[7]。

近年来，人们提出了许多识别致病SNP位点的方法[8-15]，其中性能优异的逻辑斯蒂回归及随机森林算法目前被普遍使用[13]。逻辑斯蒂回归是一种广义线性回归分析模型，解决了线性回归模型不适用因变量为离散值的问题，目前在疾病诊断、经济预测等领域应用广泛。随机森林是一个包含多个决策树的集成分类器，可显著提升模型的精度及泛化性能。但是，以上两种方法有一个共同的缺点是计算复杂度比较高，不适合实时处理数据量庞大的高维基因数据集。基于此，本文提出了利用K均值聚类算法识别遗传疾病致病SNP位点的新算法，为实时处理大规模畜禽基因数据集提供参考。

1 材料与方法

1.1 数据

1.1.1 模拟数据集 利用文献[16]提供的3种生成模拟数据集的模型。模型1具有位点乘法效应；模型2具有规律的位点交互作用；模型3具有非规律的位点交互作用。因此，由模型3生成的模拟数据集相比模型1和模型2致病位点更难识别。为了更好地验证算法性能，本试验采用由模型3生成的模拟数据集。通过调节致病率参数，数据集中嵌入了两个致病位点，编号为11和21。数据集由2 000个样本组成，其中包括1 000个健康样本和1 000个患病样本，每个样本包含1 000个位点。最小等位基因频率(MAF)值取0.2，主效应值取0.5，表示连锁不平衡程度的值取0.33。模拟数据集的详细情况如表1所示。

表1 模拟数据集详细情况Table 1 The details of simulation data set

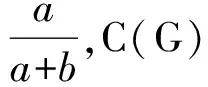
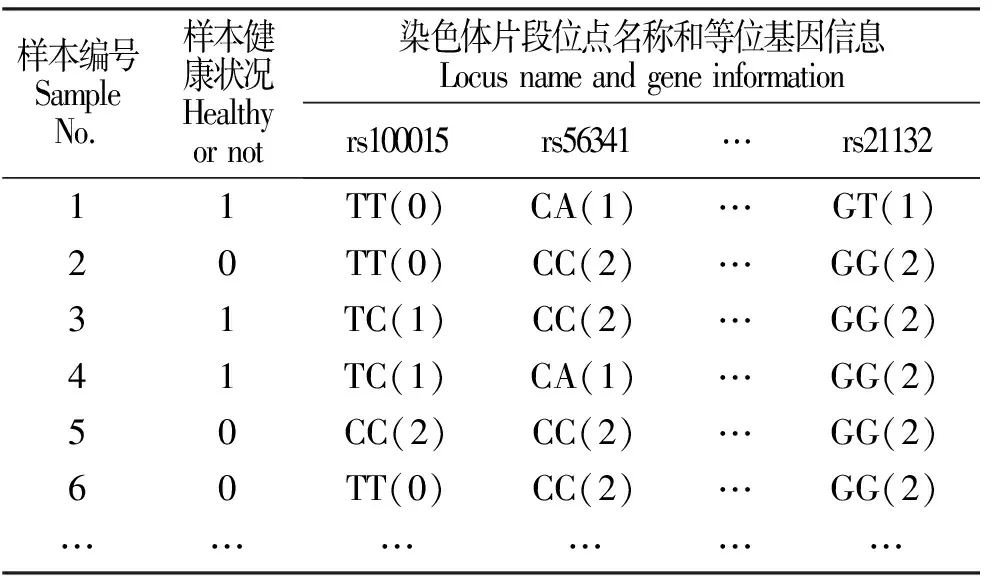
表2 真实数据集各位点数值编码Table 2 The numerical coding of all SNPs of real data set

1.2 方法

1.2.1 逻辑斯蒂回归算法 逻辑斯蒂回归(Logistic Regression)实际上是一种分类模型，采用Sigmoid函数作为后验概率分布函数对输入数据集进行分类，常用于二分类问题，由如下条件概率分布表示：

(1)

式中：X∈Rn表示输入数据向量；W∈Rn表示系数权重向量；W·X表示二者的内积；y∈{0,1}表示输出类别。

1.2.2 随机森林算法 2001年，Breiman和Cutler[18]基于决策树(Decision Tree)提出了随机森林 (Random Forests)算法。随机森林本质上是一种集成算法(Ensemble Learning)，属于Bagging类型，即通过组合多个弱分类器(决策树)的结果得到最终结果(投票),显著提高了模型的精确度和泛化性能,原因就在于“随机”和“森林”，一个使其具有抗过拟合能力，一个使其更加精准。其工作原理如下：①从数据集的总共m个特征中随机选择k(≤m)个特征，然后根据这k个特征建立决策树；②重复选择n次，建立n棵决策树；③利用每棵决策树进行预测，得到n个预测结果；④计算每个预测结果的得票数，将得到票数最高的预测结果作为随机森林算法的最终结果。

1.2.3 箱型图统计法 箱型图(box plot)是一种显示一组数据分散情况的统计图，能显示出一组数据的上下限、中位数及上下四分位数，如图1所示。

图1 箱型图Fig. 1 Box-plot

箱型图可用于识别异常值，其识别温和异常值及极端异常值的标准公式如下：

MA={x|xQ3+1.5I}

(2)

EA={x|xQ3+3I}

(3)

式中：Q1表示下四分位数；Q3表示上四位数；I=Q3-Q1；MA表示温和异常值集合；EA表示极端异常值集合。相比普遍使用的基于正态分布的Pauta准则，箱型图不受极端值影响，不需要假定数据服从特定分布，异常值识别结果比较客观[19]。为了保证致病SNP位点识别的准确性，本文采用极端异常值标准公式(3)。

1.2.4 χ2检验 χ2检验又称卡方检验[20]，其基本公式为：

(4)

式中：Ai为实际观察频数，n为样本容量，Pi为理论概率，nPi为样本理论频数。

1.2.5 K均值聚类算法 K均值聚类算法(K-means clustering algorithm)是一种迭代求解的聚类分析算法，其步骤是随机选取K个数据对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离其最近的聚类中心[21]。聚类中心以及分配给它们的对象代表一个聚类。每分配一个样本，聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程不断重复，不断降低类簇的误差平方和(Sum of Squared Error ，简记为SSE)，直到不再变化为止，得到最终结果。实际操作中终止条件通常取没有(或最小数目)对象被重新分配给不同的聚类，或没有(或最小数目)聚类中心再发生变化，或达到最大的迭代次数。

数据对象与聚类中心间的欧式距离计算公式为：

(5)

式中：X为数据对象；Ci为第 个聚类中心；m为数据对象的维度；xj和cij分别为X和Ci的第j个属性。

整个数据集的误差平方和SSE的计算公式为：

(6)

式中：k为类簇个数。

1.2.6 基于K均值聚类算法 基于K均值聚类算法、箱型图统计法及卡方检验，本文提出一种新的识别致病SNP位点的算法。该算法工作原理如下：①利用K均值聚类算法将每个位点的所有样本聚为2类，即健康样本和患病样本。②根据数据文件提供的样本类别信息，按照公式(7)计算聚类正确率。聚类正确率越高的位点说明区分健康样本和患病样本的能力越强，是致病位点的可能性越大；反之，是致病位点的可能性越小。

(7)

式中：N表示样本总数；TP表示聚类正确的健康样本；TN表示聚类正确的患病样本。

③利用箱型图统计法筛选异常值，即致病SNP位点。

④利用χ2检验进一步校验箱型图筛选出的致病SNP位点。

1.2.7 程序和运行环境 为了验证所提出的基于K均值聚类算法的性能，将该算法与当前广泛应用的逻辑斯蒂回归和随机森林两个主流算法在两个数据集上进行识别准确性及运行时间的比较。三种算法程序均采用MATLAB语言编写，其中本文编写了基于K均值聚类算法及逻辑斯蒂回归算法，分别调用了实现K均值聚类的kmeans和实现逻辑斯蒂回归的glmfit两个MATLAB内置函数；随机森林算法程序来自GitHub MATLAB程序包，参数值取缺省值。所有试验均使用64位Win10系统，在MATLAB 2016软件上进行，其中CPU为Intel(R)Core (TM) i7-4790 ( 3.6 GHz)，内存大小为8GB。

2 结果与分析

2.1 基于K均值聚类算法

2.1.1 模拟数据集 ① 聚类结果。利用K均值聚类算法对模拟数据集每个位点进行聚类并计算正确率。正确率排名前十的位点及其卡方检验统计量值如表3所示。各个位点的聚类正确率如图2所示。

表3 模拟数据集聚类正确率排名前10位点的计算结果Table 3 The details of top 10 SNPs of clustering accuracyin simulation data set

由表3可得，位点SNP11的聚类正确率比SNP21高0.09%，而比位点SNP185高3.43%，因此可以初步推断，模拟数据集位点SNP11和SNP21为疑似致病位点。

②致病位点筛选。利用箱型图统计法公式(3)筛选聚类正确率的极端异常值，即致病位点。由各个位点的聚类正确率值可以计算出箱型图极端异常值阈值上限为0.5385。由图2和表3可以筛选出致病位点为SNP11和SNP21。

图2 模拟数据集每个位点聚类正确率Fig. 2 Clustering accuracy of eachSNP in simulation data set

③卡方检验验证。利用卡方检验对箱型图筛选结果做进一步的验证。由公式(4)可以计算出每个位点的卡方值，如图3所示。

由于数据分为2类和3种基因型，所以卡方检验自由度为(2-1)×(3-1)=2。

Bonferroni原理[22]：如果在同一数据集上同时检验n个独立的假设，那么用于每一假设的统计显著水平应为仅检验一个假设时显著水平的1/n。

由于模拟数据集含有1 000个位点，所以显著水平取值为0.05/1000=5×10-5,查表可得卡方检验临界值为19.80。

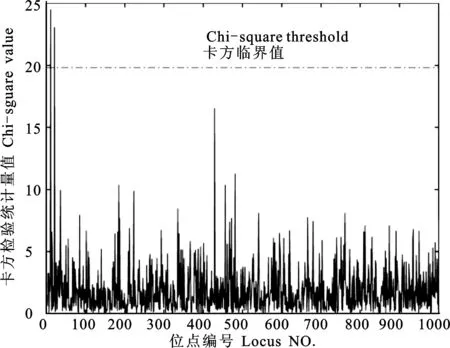
图3 模拟数据集每个位点卡方值Fig. 3 Chi square test statistic value ofeach SNP in simulation data set

由表3和图3可知，只有位点SNP11和SNP21的卡方值高于临界值19.80，这与本文提出的基于K均值聚类算法筛选结果一致。

2.1.2 真实数据集 ①聚类结果。利用K均值聚类算法对真实数据集每个位点进行聚类然后计算聚类正确率。正确率排名前十的位点及其卡方检验统计量值见表4，所有位点的聚类正确率见图4。

表4 聚类正确率排名前10位点的计算结果Table 4 The details of top 10 SNPs of clusteringaccuracy of real data set

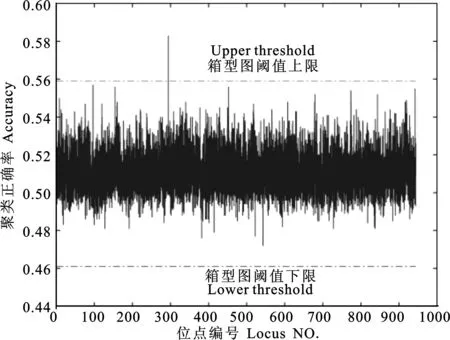
图4 真实数据集每个位点聚类正确率Fig. 4 Clustering accuracy of each SNP in real data set

从表4可得，真实数据集SNP2938位点的聚类正确率比SNP962高4.46%，而SNP962比SNP1541高0.18%，因此可以初步推断，真实数据集中位点SNP2938是疑似致病位点，其相应的位点名称为rs2273298。

②致病位点筛选。利用箱型图统计法公式(3)筛选聚类正确率的极端异常值。由各个位点的聚类正确率值可以计算出箱型图极端异常值阈值上限为0.5590。由图4和表4可以筛选致病位点为SNP2938，即rs2273298。

③卡方检验验证。利用卡方检验对箱型图筛选结果做进一步的验证。由公式(4)可以计算出每个位点的卡方值，如图5所示。由于真实数据集依然分为2类和3种基因型，所以卡方检验自由度依然为(2-1)×(3-1)=2。

依据Bonferroni原理，由于真实数据集含有9 445个位点，所以显著水平取值为0.05/9445=5.2938×10-6，查表可得卡方检验临界值为24.2979。

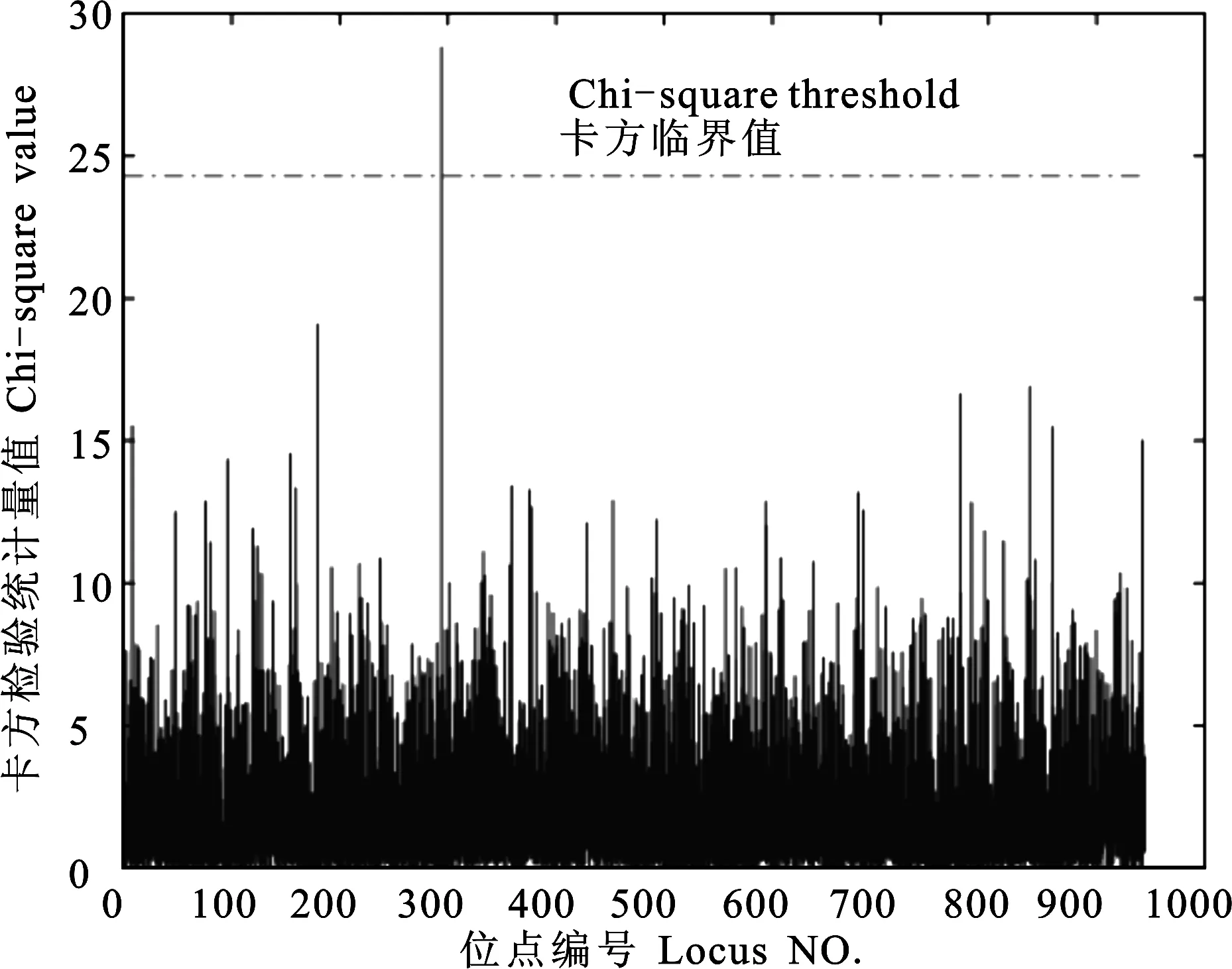
图5 真实数据集每个位点卡方值Fig. 5 Chi-square test statistic value of eachSNP in real data set

由表4和图5很容易看出，只有位点SNP2938的卡方值高于临界值，这与本文提出的基于K均值聚类算法筛选结果一致。

2.2 逻辑斯蒂回归算法和随机森林算法

2.2.1 模拟数据集 逻辑斯蒂回归算法和随机森林算法通常被用于致病位点识别[14,22-23],两种算法都选择分类正确率作为筛选致病位点的指标。分类正确率的计算方法类似公式(7)，只需将聚类换成分类即可。同样使用箱型图统计法筛选致病位点。经计算，逻辑斯蒂回归算法的极端异常值阈值上限为0.5375，随机森林算法的极端异常值阈值上限为0.5395。其中，逻辑斯蒂回归分析函数glmfit返回参数中包括P值。同样，依据Bonferroni原理，模拟数据集的显著性水平依然取值为0.05/1000=5×10-5。逻辑斯蒂回归算法分类正确率排名前十的位点及相应P值见表5。

表5 逻辑斯蒂回归算法分类准确率排名前10位点及P值Table 5 The top 10 SNPs using Logistic Regression

由表5可以看出，逻辑斯蒂回归算法准确识别出了两个致病位点，这两个致病位点也都通过了P值检验。

随机森林算法分类正确率排名前十的位点见表6。由表6可以看出，随机森林算法也准确识别出了模拟数据集的致病位点。

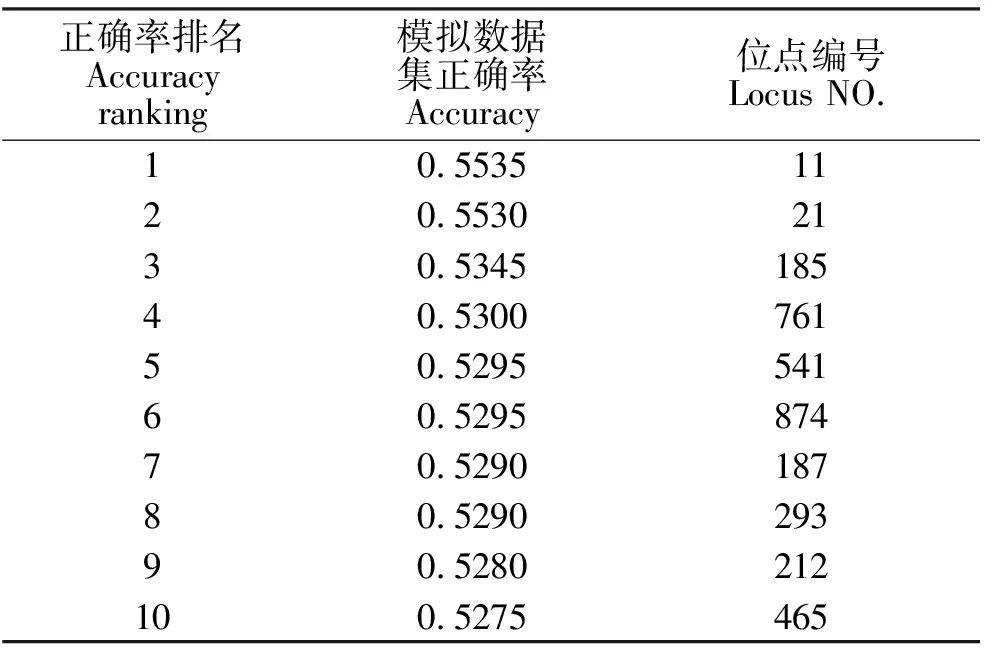
表6 随机森林算法分类正确率排名前10位点Table 6 The top 10 SNPs of classification accuracyusing Random Forest

2.2.2 真实数据集 方法和步骤与模拟数据集一样。经计算，逻辑斯蒂回归算法的极端异常值阈值上限为0.5590，随机森林算法的极端异常值阈值上限为0.5600。同样，依据Bonferroni原理，真实数据集的显著性水平依然取值为0.05/9445=5.2938×10-6。逻辑斯蒂回归算法分类正确率排名前十的位点及相应P值见表7。由表7可以看出，逻辑斯蒂回归对真实数据集也正确识别出了致病位点，这个致病位点也通过了P值检验。

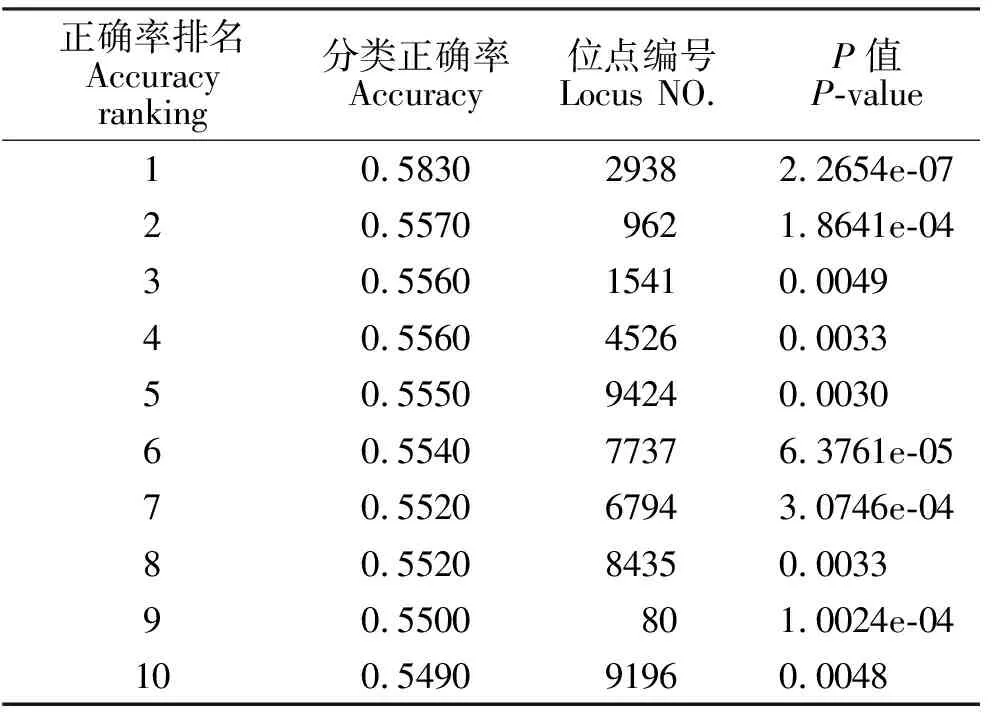
表7 逻辑斯蒂回归算法分类准确率排名前10位点及P值Table 7 The top 10 SNPs using Logistic Regression

随机森林算法分类正确率排名前十的位点见表8。由表8可以看出，随机森林算法也准确识别出了致病位点。

表8 随机森林算法分类正确率排名前10位点Table 8 The top 10 SNPs of classification accuracyusing Random Forest

2.3 三种算法程序运行时间比较

三种算法的运行时间如表9所示，其中本文提出的基于K均值聚类算法和逻辑斯蒂回归算法的数据都是运行10次取平均值的结果，而随机森林算法数据是运行一次的结果，因为随机森林算法运行时间太长。

表9 三种算法运行时间对比Table 9 Running time comparison of three algorithms s

由表9可以看出，本文提出的基于K均值聚类算法用于模拟数据集和真实数据集的运行时间相比其它两种算法都有很大的优势。

3 讨 论

本研究在对遗传位点进行数值编码的基础上，使用K均值聚类算法，结合箱型图与卡方检验，提出了基于K均值聚类算法的一种识别致病SNP位点的新方法。该方法首先利用K均值聚类计算各位点的聚类正确率，然后应用箱型图统计法筛选出致病SNP位点，再用Bonferroni原理和卡方检验对结果做进一步的校验。最后与逻辑斯蒂回归算法和随机森林算法进行了比较。

在识别结果方面，三种算法均准确识别出了致病位点，与方雅兰[14]、陈剑[22]和王宇琛等[23]研究结果一致。在阈值方面，对模拟数据集，随机森林算法阈值优于本文提出的基于K均值聚类算法及逻辑斯蒂回归算法；对真实数据集，本文提出的基于K均值聚类算法及逻辑斯蒂回归算法阈值优于随机森林。在运行时间方面，对模拟数据集，逻辑斯蒂回归算法大约是本文提出的基于K均值聚类算法4倍；对真实数据集，逻辑斯蒂回归算法大约是本文提出的基于K均值聚类算法12倍。对模拟数据集，随机森林算法大约是本文提出的基于K均值聚类算法670倍；对真实数据集，随机森林算法大约是本文提出的基于K均值聚类算法1000倍。因此，在运行速度方面，相比逻辑斯蒂回归算法和随机森林算法，本文提出的基于K均值聚类算法优势巨大，并且数据集规模越大优势越大。K均值聚类算法优势巨大的原因是：K均值聚类算法的复杂度为O(N)，而逻辑斯蒂回归算法的复杂度为O(NlogN)，随机森林算法的复杂度为O(MNlogN)，其中N为样本数，M为树的棵数。

本文提出的基于K均值聚类算法不但可以识别致病位点，也可以识别致病基因，借助其速度优势可用于畜禽遗传疾病的大规模检测，对预防遗传疾病在畜禽中的散播，净化谱系，提高选种准确性，加快畜禽育种进展，进而提高畜牧业生产水平具有重要意义。