燃动脑神经 传扬新思维——《跟张天孝爷爷学数学》教学实录及评析

孙维佳 陈嘉禾

【教学内容】

《跟张天孝爷爷学数学》（1B）第115 页。

【教学过程】

一、燃动大脑，观察算式

1.出示：（）×6+6=3×6。

师：同学们，乘法大家已经很熟悉了吧，你能猜出花朵后面藏着谁吗？

生：3×6=18，18-6=12，2×6=12，所以花朵后面藏着2。

师：这个方法不错，有没有不一样的想法呢？

生：3×6 表示3 个6，几个6加1 个6 等于3 个6 呢？2×6+6=3×6，所以花朵后面藏着2。

师：从计算的意义来思考，又快又好。其他同学可以像这样，找出第二朵花后面藏着几吗？

2.出示：（）×6-6=3×6。

生：4 个6 减1 个6 等于3个6，也就是6×4-6=3×6，这朵花后面藏着4。

师：谁愿意用这种方法再来试一试？

3.出示：（）×6-6=4×6。

生：5 个6 减1 个6 等于4个6，这朵花表示5。

师：原来不用算，直接看乘法的意义就能解决问题，真是太好了！

师：看一看，你能找到这个叶片后面藏着几吗？

4.出示:2×4+16=（）×4。

生：2×4 表示2 个4，16=4×4，也就是4 个4，2 个4 加4 个4一共6 个4，叶片表示6。

师：你说得真好。老师找来点子图帮忙（出示点子图的动态变化过程），请大家一起看看这个推算的过程——

生：原来的点子图是2 个4加16，把16 个点子变成4 个4，2个4 加4 个4 就是6 个4。

【评析：复习导入，巩固学生对乘法意义的理解，在此基础上，给出变式挑战：2×4+16=（）×4，通过资优学生的引领，配合点子图演示，鼓励学生积极思考，突破难点，为后续的学习做铺垫。】

二、触动神经，感悟推理

1.初识问题，明确题意。

师：现在把我们学过的加减乘除都集中在一个竖式中，你们能看明白吗？

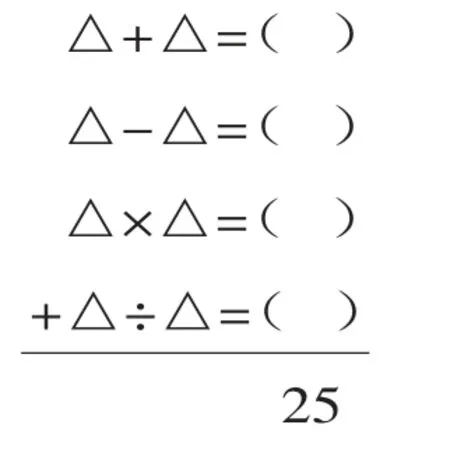
△表示一个相同的数，△=？

（学生观察一分钟）

师：谁看明白了？

生：大家看这条横线，横线上面有加法算式的和、减法算式的差、乘法算式的积、除法算式的商，然后这四个算式的结果相加，就等于25。

师：就是每个算式的得数相加等于25，那这几个得数分别是多少呢？请从你认为最容易找出得数的算式开始。

生：△表示同一个数，一下子就知道了减法算式，同数相减等于0；除法算式，同数相除等于1。

师：真能干！无论△是几，两个相同的数相减，差一定是0；两个相同的数相除，商一定是1！

师：那剩下乘法的积和加法的和又是多少呢？请和你的同桌合作，看看能不能解决。

2.合作探索，优化方法。

（1）同桌合作探索三分钟。

（2）学生交流反馈。

师：谁来揭秘一下？你们是怎么想的？

生：我从1 开始一个一个试，△=1、△=2、△=3、△=4，试到4的时候，发现和、差、积、商加起来等于25，所以我发现△=4。

师：逐个尝试，是一种办法。还有其他方法吗？

生：我也是试一试，不过我是从4 开始试的。

师：你为什么从4 开始试？

生：和、差、积、商的总和是25，而差=0，商=1，那么和+积=24，△×△的积应该比24 还要小。五五二十五，所以△肯定比5小。我猜想△会不会是4 呢？试一试，发现△=4 正好符合题目的所有要求。

师：真是个好方法。谁听明白了？谁愿意再来说一说？

师：刚才两位同学的方法，谁的更好呢？

生：我觉得第二种方法更好，第二种方法分析了以后，试起来更准确、更快。

3.观察理解，沟通图式。

师：我们再请点子图来帮忙。

出示代入△=4 后的竖式，分步出示每个算式对应的点子图。

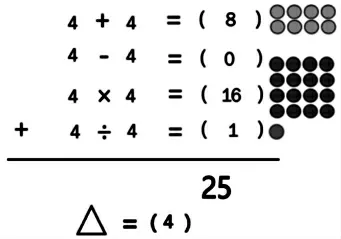
师：4＋4 就是2 个4（出示两排4 个点子）；4-4=0，没有了；4乘4 也就是4 个4（出示4 排4个点子）；4÷4=1，出示1 个点子。

师：把这些点子移一移、理一理（展示点子图移动变化的过程）。现在，你还能从这幅点子图里把加减乘除四个算式的对应部分找出来吗？谁愿意上来圈一圈，说一说？

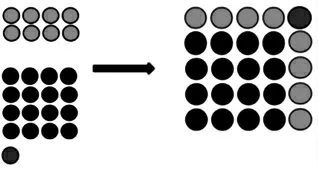
（一位学生上台，边圈边按和差积商逐个说明）

师：推算过程中想到的五五二十五，你在图中看到了吗？

生：这个点子图表示的就是5×5。

师：同学们真是太厉害了！通过回忆口诀，锁定了△的大小，经过检验，很快揭晓了这个竖式的答案。最后，我们发现，这个竖式还对应了一个神奇的点子图。同学们，这个竖式神奇吗？

（揭示课题：神奇的竖式）

【评析：竖式的表现形式比较复杂，所以先集体审题，明确题意，帮助学生确定思考的方向，在此基础上，鼓励学生合作思考、交流探究。反馈环节中，鼓励学生表述不同的思考过程，让学生在充分对比中优化解决问题的方案。最后，教师通过分别出示每个算式的点子图，以及移动点子合成竖式的动态过程，支撑学生理解数、 式的整合变化原理，为进一步学习和丰富思维图式奠基。】

三、激动思维，发现规律

师：你能独立解决下面的竖式吗？完成这两个神奇的竖式，并在点子图中把神奇竖式中的加减乘除四个算式对应的部分圈一圈。

出示：

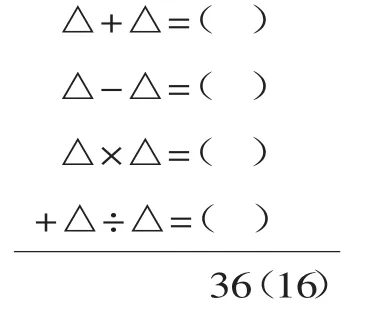
师：你是怎么想的？

生：六六三十六，△肯定比6小。我再倒推一个数——5，试验5 发现正确。

生：四四十六，△比4 小。我再倒推一个数——3，试验3 发现正确。

师：（整体出示三个竖式和对应的点子图）仔细观察这几个神奇竖式，你有什么发现？

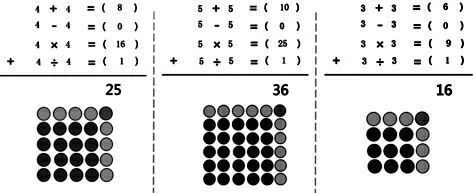
生：神奇竖式对应的点子图都是一个几×几的方阵，且神奇竖式中三角形都是这个几减去1。

师：原来神奇竖式的点子图就是一个方阵，这个竖式真是太神奇了！

【评析：波利亚说“数学有两个侧面，一方面它是欧几里得式的严谨科学，从这个方面看，数学像一门系统的演绎科学； 但另一方面，创造过程中的数学，看起来是一门实验性的归纳科学”。借助点子图，数形结合，引导学生在观察、尝试和反思中，不断发现新的结论，生成新的知识。】

四、促动发展，自主创新

师：老师这儿还有一个竖式，和我们神奇的竖式很像——

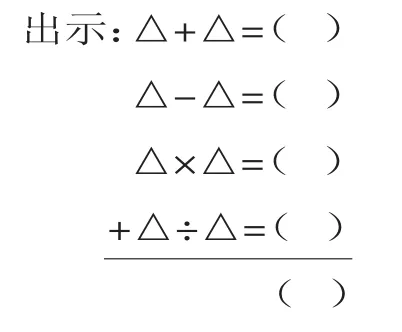
生：少了和差积商的和。

师：你们能补充一下这个和吗？根据前面的经验，想一想：和可能是多少？

生：49、64、81。

师：你们是怎么想的呢？

生：因为我们刚刚发现神奇竖式的点子图是一个方阵，所以神奇竖式中和差积商的和一定是一个平方数。像三三得九，四四十六，五五二十五这样的数。所以我们猜，只有49、64、81 这些数才可能是这里的和。

师：同学们真了不起，还注意到这个和就是一个平方数！大家不仅能够揭秘这样的神奇竖式，还能自己创造竖式，老师为你们点赞！

【评析：本环节中包含两个层次的练习，通过基础练习帮助学生巩固新知，进而引导学生自创竖式，在开放性练习中拓展学生的思维，激励他们的创新意识。】

【教学综述】

张天孝老师说过，“数学教育的本质就是思维训练”。《跟张天孝爷爷学数学》以张老师与一名学龄儿童一起学习数学的过程为场景依托，通过重组数学知识结构、更新内容、滚动发展的方式，让儿童在掌握和应用知识的过程中发展思维，培养良好的品格。目前，我们正在尝试依托《跟张天孝爷爷学数学》，进行集体化的数学拓展性课程实施路径的探索。在课堂上，我们发现：好的数学材料不仅是知识的载体，更是引燃学生思维火花的导线，同时激发教师改变课堂的教学方式。

本课以小游戏的形式启动导入，激活学生对乘法的认知，激发学生探索新知的兴趣。在导入中即引出几乘几的点子图的变化来向学生渗透数形结合的意识和方法，为后面的学习做铺垫。第一次呈现综合竖式时，先引导学生明确题意，降低参与门槛，使更多的学生能够在课堂学习的时间里，有效参与思考和讨论。通过小组合作，初步形成解题策略，在此基础上，通过对两位学生思路的对比，优化解题的过程。进一步，以“竖式——点子图”数形结合的方式，赋予数的知识以几何直观，帮助学生发现竖式中四个算式和差积商之和的本质就是一个平方数，进而推演△和这个平方数之间的关联。最后，学生们进行竖式的水平应用和拓展设计练习，不同层次的学生获得不同层次的发展。

这次研讨活动，我们进行了前后测比较，发现课后学生的解题策略和正确率远优于课前，特别是，学生数形结合的解释能力和应用能力有了提升。我们在“神奇的竖式”这一拓展性内容中再次看到，学生的数学思维发展存在巨大的可能性，教师应立足核心素养和创新思维品格的发展来设计课、实施课，给学生创造优质的学习和发展机会。