感知变量关系 理解比例意义
——《比例的意义》教学设计新策略
2021-01-07邵爱珠
邵爱珠
函数是描述客观世界变化规律的重要数学模型。函数思想方法是运用运动和变化的观点、集合和对应的思想去分析问题的数量关系,通过类比、联想、转化合理地构造函数,运用函数的图象和性质,使问题得以解决。函数思想的核心是事物的变量之间有一种依存关系,一个量随着另一个量的变化而变化,通过对这种变化的探究找出变量之间的对应法则,从而构建函数模型。虽然在小学中没有正式引入函数概念,但函数的思想、雏形随处可见。
比例知识呈现了生活和数学中最基本、最常见的数量关系和变化规律,是重要的数学模型,蕴含了基本的函数思想。一般的关于比例意义的教学设计,都是基于静态的数据比较引出概念,那么如何关注数量间的变化规律,从渗透函数思想的角度来设计《比例的意义》教学呢?
一、创设情境,感知对应关系
1.观察情境,初始对应。
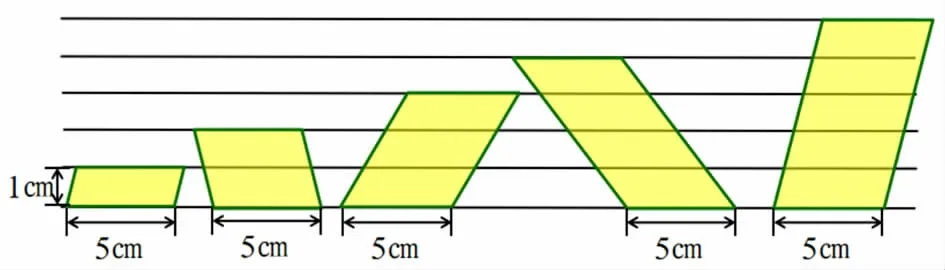
师:这里有一组平行四边形,从图中你了解到哪些信息?有什么发现?
2.梳理情境,完善数据。
师:这组平行四边形底边都为5cm。请认真观察,试着填完整下表:

面积(cm2)5高(cm)1
【设计意图:在一组平行线中呈现五个大小、形状各异的平行四边形,用简单、熟悉的素材唤起学生对两个对应量变化关系的思考。这组平行线之间的间隔都是1 厘米,学生从直观可以发现:当底边长度不变时,平行四边形的面积随着高的增加而不断变大,初步感知高和面积的对应关系。】
二、自主探究,发现变化规律
师:仔细观察图和表,说说你有什么发现?
1.先独立思考,想一想、算一算;然后把你的发现在小组中交流。
2.全班交流。
3.梳理回顾学生的发现,预设可以得到以下几种发现:
(1)平行四边形的底不变,面积随着高的变化而变化。
(2)平行四边形的底不变,高越长,面积越大;高越短,面积越小。
(3)平行四边形的面积与高的比值都是5。
(5)平行四边形每增加1 厘米的高,面积就增加1 个5 平方厘米。
【设计意图:已知平行四边形的底与高计算面积,是学生已有的知识基础,通过学生对熟悉的素材的自主探究、合作交流,尝试从数据中进一步发现两个对应量之间的关系,渗透函数思想。同时,不断挖掘原有知识中的新问题,用学生自己的方式架构起与新知的联系。】
三、抽象建构,理解比例意义
师:这里的每个平行四边形的面积与高之间的比值都是5,如5∶1=5、20∶4=5。像这样两个比的比值相等,也就是两个比相等,我们可以用等号连接,写作5∶1=20∶4。这样的等式,叫做比例。
师:从刚才的这些数据中,你还能组成哪些比例?试着写一写。
交流反馈学生作品后,引导归纳:
1.这组数据中,底边长度不变,每个平行四边形的面积与高之间的比值都是5。因此任意两个平行四边形的面积与高的比都可以组成比例,如5∶1=20∶4、10∶2=15∶3、25∶5=20∶4 等。
2.从数据中还可以得到:底边长度不变,每个平行四边形的高与面积的比值也是相等的,都是因此任意两个平行四边形的高与面积的比也可以组成比例,如1∶5=4∶20、2∶10=3∶15 等。
3.迁移:如果继续往下画图,你还能根据图的规律,试着再写出几个比例式吗?
师:用自己的话说一说什么是比例?
【设计意图:这是本课的重要环节,从学生已有的解题经验出发,借助对“相等的比”的理解、掌握,为建立比例概念做知识铺垫。在此基础上抽象建构比例的概念,就显得顺理成章,条理更清晰、结构更严谨。“根据图的规律尝试再写几个比例式”是基于对这组有关联的数据的充分利用,运用发展、变化的观点,进一步感知两个对应量之间的依存关系,帮助学生在解决问题过程中感悟相关联的量,从而进一步理解比例的意义。】
四、练习拓展,巩固比例意义
1.基础练习,在模仿中理解比例。
算一算、选一选:下面各表中相对应的两个量的比能组成比例的是()
A.
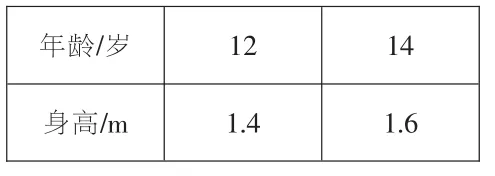
B.
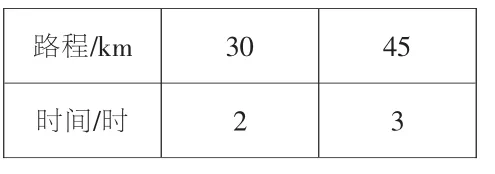
C.
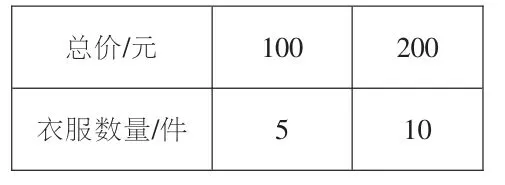
D.
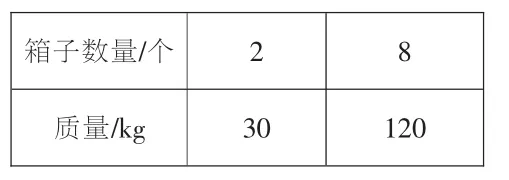
2.综合练习,在感知中巩固意义。
(1)画一画、填一填。
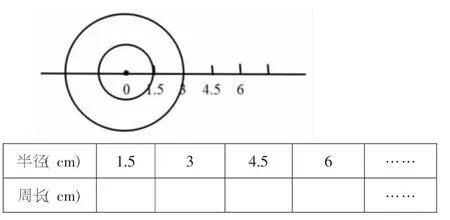
(2)从上表中选几组数组成不同的比例。
【设计意图:习题2 改编自西南师大版教材:先根据提示画一画,画出不同半径的圆,再分别算出每个圆的周长,在此基础上选出几组数据组成不同的比例。这一题将比例的知识与学生已有的圆的知识建立起联系,在解题的过程中伴随动手操作,多种感官参与学习,能充分调动学生的学习兴趣,既让学生在练习过程中强化比例的意义,同时也进一步感悟圆周长与半径之间的关系。在数据的选择上也凸显了这一题独有的价值,尽管很多练习也充分考虑了数据的类型,涉及整数、分数、小数,尽量体现数据的丰富性,但对于像π 这样的无理数很难呈现。编制这道习题,不仅变化了习题的呈现方式,更丰富了数据的类型,同时在练习中进一步感知了对应量的关联性。】
3.提高练习,在变式中理解意义。
用下图中的4 个数据可以组成多少个比例?试着写一写。
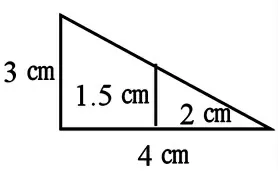
整个教学设计,试图让学生在经历观察、比较、思考、交流的过程中,逐渐体会到相关联的两个量之间的相互依存、相互对应的关系。通过学习,体会到“当一个量不变时,另一个量与结果的变化是有规律的”;两个量形成比,如果比值一定,可以用等式表示,这个等式就是比例。这样的设计,既关注了知识的体验过程,又渗透了函数思想。
