把握知识关联 实现整体建构
——《平行四边形的面积计算》教学设计与说明
2021-01-07刘霞
刘 霞
【教学内容】
人教版五年级上册第87~89页。
【教学过程】
一、情境导入,引发猜想
师:王大叔用4 根围栏围了一个长方形花圃(如图①)。已知这个长方形的长是6 米,宽是4米,你能提出哪些数学问题?
生1:这个花圃的周长是多少米?
生2:它的面积是多少平方米?
师:是的,研究平面图形我们一般既要研究它的周长,也要研究它的面积。它的周长是多少?
生:(6+4)×2=20(米),它的周长是20 米。
师:面积呢?
生:6×4=24(平方米),面积是24 平方米。
师:后来因为修路,王大叔把这个花圃的形状改变了一下(课件演示把长方形拉成一个平行四边形,如下图②)。变成了什么?
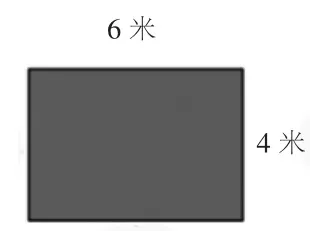
图①
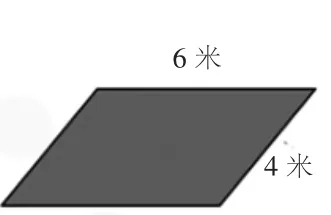
图②
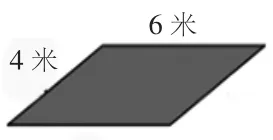
图③
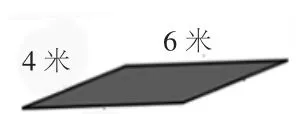
图④
生:(齐)平行四边形。
师:从刚才的变化中,你有什么发现吗?
生1:它的周长没变,是20米。因为平行四边形的四条边就是长方形的四条边。
生2:它的面积好像变小了。
师:是吗?我们不妨再变一变。(将图②继续拉成图③)你有什么发现吗?
生:它的周长没有变,都是20 米。但是,这时的面积变得更小了。
(教师继续操作,将图③变成图④,进一步增强学生对“周长不变,面积变小”的直觉感受)
师:连贯起来看,后面三个平行四边形的面积变得越来越小了。那每个平行四边形的面积到底是多少?平行四边形的面积计算到底与什么有关?这就是我们今天要研究的问题。
【说明:课堂教学的素材要简约、经济、精炼。课始创设了4 根围栏围长方形花圃的生活情境,在复习周长和面积等知识基础上,通过三次情境变化——将长方形不断拉“矮”,从而形成认知冲突,产生进一步探究的需要。】
二、实践操作,归纳推理
1.动手操作,初步感知转化。
师:为了便于研究,我给大家提供了一份方格图,每个方格的边长是1 米。你能通过数一数、画一画或者剪一剪的方法得出图②的面积吗?
(学生动手操作、探究,小组讨论、交流)
生:我是先数出图形中不满一格的一共是10 个,10÷2=5(格),正好能拼成5 格,然后用13+5=18(格),面积就是18 平方米。
师:不满一格算半格,是我们计算不规则图形的面积的一种很好的方法。
生:我是将这些不完整的方格拼成了完整的方格。然后数一数,一共有18 格,每格1 平方米,一共是18 平方米。(如图⑤)
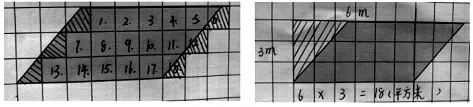
图⑤

图⑥
生:我是沿这条线将平行四边形剪出了一个直角三角形,然后将它向左平移,拼成一个长方形。这个长方形的长是6 米,宽是3 米。然后用6×3,就得出它的面积是18 平方米。(如图⑥)
师:同学们,我们一起来观察一下,同样是割补的方法,有什么不同之处,哪种方法更简便?
生:第一个同学是一个一个割补的,而第二个同学是整体割补的,所以第二种方法更简便。
生:我的方法是沿这条线将平行四边形分成了两个直角梯形;然后把左边的梯形向右平移,也拼成了一个长方形。长是6 米,宽是3 米,面积是18 平方米。(如图⑦)
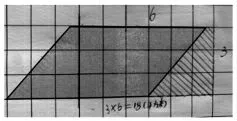
图⑦
师:仔细观察这两种方法,他们都是沿着平行四边形的什么剪的?
生:高。
师:如果不沿着高剪可以吗?为什么?
生:不行,因为只有沿着高剪开,才能将它拼成一个长方形,根据长方形的面积我们才能得到平行四边形的面积。
师:是啊,沿着高剪开就可以把平行四边形转化成一个面积相等的长方形,化未知为——(已知),化陌生为——(熟悉),从而解决了问题。转化是一种很重要的数学思想。
【说明:为学生提供带有方格的平行四边形,放手让他们根据自己的实际经验选择不同的方法,并把自己思考的过程展现在《作业纸》上,符合学生的实际水平,也能让所有学生都参与其中。然后根据学生几何思维的发展水平逐次呈现典型作品,学生在分享、 对比中经历了从单位面积的转化到整体割补转化的过程,并在多样化中寻找到统一性(沿着“高”切拼)这一核心和关键。】
2.深入感知,归纳推导公式。
师:现在你能用转化的方法求出图③这个平行四边形的面积吗?
(学生操作、展示、交流)
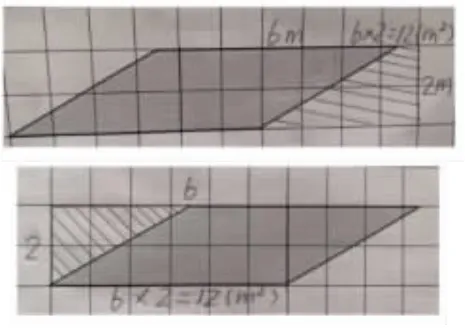
师:看来啊,不管是什么样的平行四边形,只要沿着它的高剪开,都能转化成一个长方形。求平行四边形的面积,就变成了求什么呢?
生:(齐)长方形的面积。
师:每个平行四边形的背后都隐藏着一个与它面积相等的长方形。长方形的面积=长×宽,那平行四边形的面积等于什么呢?
生:平行四边形的面积=底×高。
师:为什么?
生:因为长方形的长就是原来平行四边形的底,长方形的宽就是原来平行四边形的高,长方形的面积=长×宽,所以平行四边形的面积=底×高。
师:听明白他的意思了吗?把你们的推导过程在小组里再说一说。
(学生交流)
师:谁再来说一说?
根据学生的回答形成板书:

师:现在能看出平行四边形的面积计算到底与什么有关吗?
生:平行四边形的底和高。
师:如果用S 表示平行四边形的面积,用a 和h 分别表示它的底和高,平行四边形的面积公式用字母就以表示成什么?
生:(齐)S=a×h。
师:谁能直接计算出图④这个平行四边形的面积?
生:6×1=6(平方米)。
师:你能解释一下,为什么可以这样计算吗?
生:把平行四边形沿着这条高剪开,就能拼成一个长方形,这个长方形的长是6 米,也就是原来平行四边形的底,宽是1 米,也就是原来平行四边形的高,所以用6×1 就能算出它的面积了。
师:看来每一个平行四边形的背后都隐藏着一个面积相等的长方形。
【说明:教师通过后两个平行四边形的面积计算,由浅入深地帮助学生深化对平行四边形面积计算的理解,引导学生发现“其实每一个平行四边形的背后都隐藏着一个长方形”,影响平行四边形面积的是底和高这两个条件。】
三、巩固练习,深化理解
1.基础性练习。
师:你能找出下面平行四边形背后隐藏的长方形,并计算出它的面积吗?
分别出示:
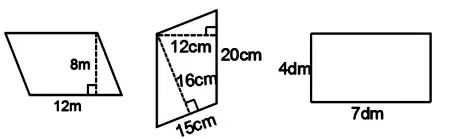
(学生练习,汇报)
师:(指第二个平行四边形)它的面积是多少?
生1:我沿着这条高(12 厘米)剪开,把它转化成了一个长20 厘米、宽12 厘米的长方形,所以它的面积是12×20=240(平方厘米)。
生2:我沿着这条高(16 厘米)剪开,把它转化成了一个长是15 厘米、宽是16 厘米的长方形,面积是15×16=240(平方厘米)。
师:你们听明白了吗?为什么会出现两种思路呢?
生:平行四边形有两组对边,每组对边都有各自的高。
师:把平行四边形沿着不同的高剪开,就可以转化成形状不同的长方形。原来,每个平行四边形后面隐藏着什么?
生:两个不一样的长方形。
师:(指第三个图形)这是平行四边形吗?
生:是的,它是特殊的平行四边形。
师:平行四边形的底是多少?高是多少?
生:它的底就是长方形的长,7 分米;高就是长方形的宽,4 分米。
师:那面积就是多少?
生:7×4=28(平方分米)。
师:同学们,长方形是一种特殊的平行四边形,其实,我们以前学习的长方形的面积等于长乘宽,就是平行四边形面积计算的一种特殊应用。而这种特殊应用又帮助我们今天推导出了平行四边形的面积计算。真是“数学很奇妙,关系最重要”!
【说明:课堂练习是学生深层次理解知识、 完成知识建构的过程。本环节遵循“从一般到特殊”精心设计了三道题目,前两道题着重基础,尤其是第二题通过两种不同的计算方法,强调平行四边形的底和高的对应关系。第三题立足于“长方形就是特殊的平行四边形”,感知两者间的联系。将长方形的面积计算纳入平行四边形的面积计算,既突出了本节课的学习重点,又帮助学生实现了知识的整体建构,彰显了数学的简洁和逻辑。】
2.例题回顾。
师:现在你能解释为什么王大伯围花圃时,周长不变,面积却为什么越来越小了吗?
生:因为它的高越来越矮了。
师:谁能说得具体一些?
生:原来它的高是4 米,后来变成了3 米、2 米、1 米,而它的底没有变,所以它的面积变小了。
师:(指着最后一个平行四边形)如果把它再往下拉,它的面积会怎么样?
生:越来越小,最后变成了一条线段。
师:那如果把它拉高呢?
生:面积就会越来越大。
师:什么时候面积最大呢?
生:当它被拉成一个长方形时,它的面积最大。
生:当它的高变成长方形的宽时,它的面积最大。
师:也就是当它的高越来越大,越来越大,最后与这条边线重合时,它就变成了长方形,这时它的面积就最大了。瞧,图形的变化让我们又有了新的发现。
【说明:例题的回顾是对学习内容的总结和再认识。学生通过对比、反思,深切地感悟到平行四边形的“高”在面积计算中的特殊意义,从而帮助他们打破长方形、正方形面积计算时建立起来的根据图形的边线长度计算面积的思维定势。】
3.变式练习。
师:这儿还有一个长方形,睁大眼睛看一看,它有了什么变化呢?
(将长方形变成等底等高的平行四边形)

生:我觉得它的形状变了,但它们的面积没有变。
师:为什么呢?
生:因为平行四边形的高就是长方形的宽,它的底就是长方形的长,所以它的面积没有变。
4.再次对比。
师:(出示例题图和刚才的练习图)对比一下这两组图形的周长和面积的变化,你有什么新的发现吗?
生:我发现第一组图形的周长不变,面积变了。而第二组图形的面积不变,周长变了。
生:第一组图形周长不变,是因为图形的四条边长度没变,但是面积变了,是因为底虽然相等,但是高变得越来越小,面积也就越来越小。而第二组图形正好反过来了,底和高都没变,面积就不变,但是因为四条边的长度在变,周长自然就跟着变化了。
师:你总结得真好!看来,图形的变化中真的大有玄妙。
【说明:图形的等积变形和长方形框架的拉升是教材中分开编排的。本节课将它们融合在一起,虽然变化得到的都是平行四边形,但是不同的变化形式,所得到的结果却大相径庭,引导学生发现“变化之中有玄妙”,既强化了新知学习,又突出了面积和周长计算的本质要素,达到了整体建构的目的。】
四、全课总结,拓展延伸(略)
