不同转速下低速重载齿轮动态磨损特性研究

卢 玲

(吉林电子信息职业技术学院，吉林 吉林 132021)

0 前言

齿轮作为重型机械领域中应用最为广泛的传动部件之一，其使用寿命直接关系到机械的整体寿命。磨损作为不可避免的一种故障形式，准确预测齿轮磨损过程对齿轮寿命分析具有重要的研究意义。在低速重载条件下，齿轮表面油膜难以形成，齿轮的主要磨损形式为粘着磨损，导致齿轮表面产生严重磨损[1]。无法准确估计齿轮表面磨损发展过程将导致齿轮有过度的冗余设计，进而导致机械重量增大，成本增加，运行与维护难度大。Flodin等人针对齿轮粘着模型进行了研究，将Archard磨损模型引入到齿轮磨损计算中，提出了齿轮磨损的计算模型，为齿轮磨损问题奠定了基础[2-4]。潘东等人充分考虑了齿轮负载及转速对齿轮副齿面磨损的综合影响，建立了齿轮磨损寿命预测模型，但仅仅考虑了单一齿轮在恒定工况下的齿轮磨损寿命预测[5]。冯松等人对齿轮齿面磨损对齿轮刚度的影响进行了分析，结果发现磨损对齿轮刚度的影响可以忽略，该研究对齿轮磨损后刚度计算的简化提供了依据[6]。周长江等人则针对圆柱斜齿轮提出了在准静态和动态载荷下的粘着磨损计算，并计算出磨损后的动力学特性[7]。本文结合Archrad磨损模型，充分考虑齿轮的内部和外部激励，得到齿面的动态载荷分布，从而计算齿轮齿面磨损分布。

1 磨损模型

粘着磨损计算首先是由Archard提出，计算粘着磨损公式为[8]

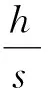
(1)

式中，h为磨损厚度；s为相对滑动距离；k是磨损系数；p为触压力；由式(1)可以得

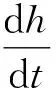
(2)

式中，v是滑动速度；在齿轮磨损计算中需要进行离散化分析，可以得到离散化齿轮磨损计算公式为

hi,j=hi,j-1+kpi,j-1vjΔt

(3)

式中，hi为i微元内的齿轮磨损深度，i为啮合点所在单元，j为p点的磨损次数；p为啮合点所受压强；vp为啮合点滑动速度；Δt为时间步长。齿面磨损离散化模型具体如图1所示。

图1 齿面离散化

图中θ1和θ2为齿轮旋转角度；v1和v2为齿轮齿面线速度，vp=v1-v2。

2 齿轮动力学模型

本文以直齿轮为研究对象，建立2个自由度的动力学模型，分别为内外齿轮的角位移θ1和θ2，具体如图2所示。其中，Rb1、Rb2分别为外、内齿轮基圆半径；T1、T2分别为输入、输出力矩；I1、I2分别为外、内齿轮转动惯量；m1、m2分别为外、内齿轮的质量；Ke(t)为齿轮时变啮合刚度；c(t)为时变啮合阻尼；e(t)为齿轮齿廓误差；f(δ)为齿轮应变函数。

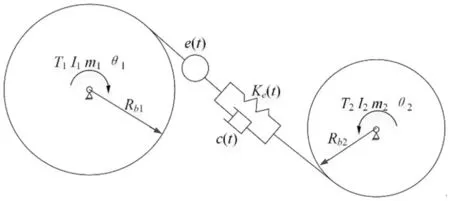
图2 内啮合直齿轮动态啮合模型

为求解动态啮合力，将角位移θ1、θ2转化为啮合方向的线位移y1、y2。假定Fd表示外部载荷力，则Fd满足Fd=T1/Rb1=T2/Rb2可得[9]

(4)

式中，S1i=ρ1i/Rb1，S2i=ρ2i/Rb2分为外、内齿轮啮合点处曲率半径与其基圆半径之比。

对于任意啮合齿对i，其动态啮合力可以表示为

Fi=Kei(xr-e)

(5)

其中，当xr-e≤0时齿轮啮合点处的啮合力为0，当xr-e>0时Fi>0。

将式(6)代入式(5)整理后可得

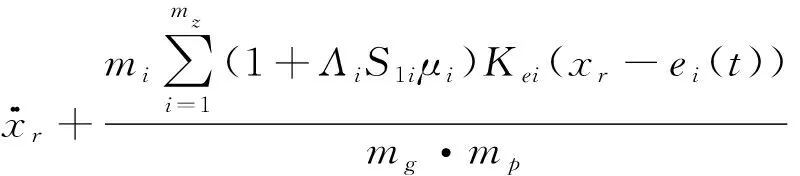
(6)

将粘性阻尼考虑进去整理后可得

(7)

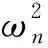
3 齿轮啮合刚度

根据最小势能原理可以准确求解出齿轮啮合刚度。通过计算在齿轮接触过程中的各应变势能，累加后得到总应变势能，从而计算总的接触刚度。计算的直齿轮轮齿的弹性势能U可以表示为弯曲势能Ux、挤压势能Un和剪切势能Us[11]：

U=Ux+Un+Us

(8)

所有的势能可以通过弹性理论公式进行计算：

(9)

式中，F为两齿间法向接触力；ξP为P点压力角；B为齿轮轴向宽度；E为弹性模量；G为剪切弹性模量；y为齿轮截面旋转中心坐标；e(y)为y的函数，表示y对应的齿轮截面齿厚；yb和yP分别为根截面和载荷截面对应的值；Cs为当量修正系数，这里取值为1.5；具体参数如图3所示。

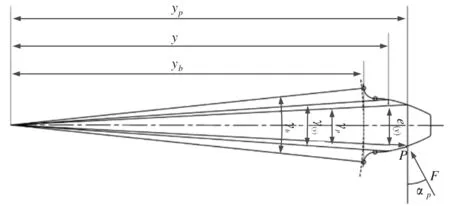
图3 齿轮几何参数

可以将U转化为关于啮合压力角ξP的函数，计算公式为

式中，ξP与啮合参数有关，γb为齿轮根部角厚度。

在齿啮合过程中会出现多对齿同时参与啮合的情况，得到多齿弹性势能Uz。

(10)

式中，在当齿轮啮合点的啮合参数为ξP时，其相邻齿面啮合点参数分别为ξP+1和ξP-1。为得到不同轮齿的齿面载荷，定义Us的逆函数Vs满足以下条件

(11)

4 齿面磨损计算

主动轮齿轮模数为5.5，压力角为0.35 r/min，输入功率为50 kW，其他参数如表1所示。

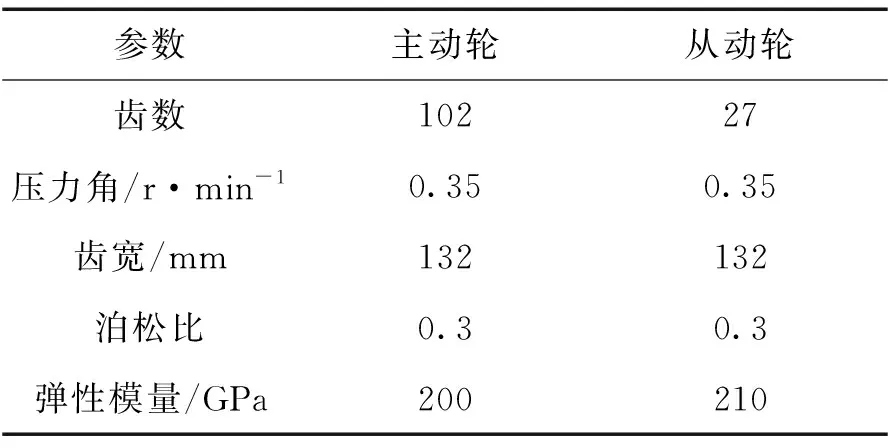
表1 齿轮参数

将齿轮从进入啮合到退出啮合等间距分割成100个时间步长，并假设每个时间微元内认为齿轮齿面几何参数不变。为求解齿轮运行过程中的齿面动态载荷随时间变化的函数，需要求解出齿轮齿面的稳态载荷分布，并结合龙格库塔法进行迭代求解。计算流程图如图4所示。

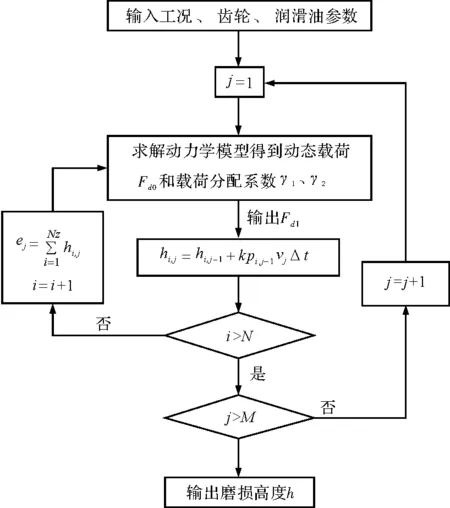
图4 齿轮表面磨损流程图

根据最小势能法可以计算得到齿轮稳态状态下的齿面啮合力，并作为计算迭代的初值进行计算。同时为研究不同转速下对齿轮磨损的影响，分别计算在主动轮转速分别为10 r/min、40 r/min、70 r/min时的啮合力,如图4所示。

图5 齿轮齿面滑动速度和齿面啮合力

图5中Tz为轮齿啮合周期。可以看出齿轮在单-双齿啮合过程中两次明显突变。而在动态条件下的低速齿轮齿面啮合力如图6所示。

图6 齿轮齿面滑动速度和齿面啮合力

从图6中可以看出，在功率不变时，齿轮转速增加齿轮齿面啮合力从10 r/min时的多峰分布逐渐转变为30 r/min和0 r/min时的双峰分布。此时齿轮齿面啮合力呈明显的动态特征。

分别计算转速为10 r/min、30 r/min和50 r/min时，主动轮和从动轮经过10 000、20 000、…、100 000次啮合厚度的齿轮表面磨损分布，如图7～图12所示。

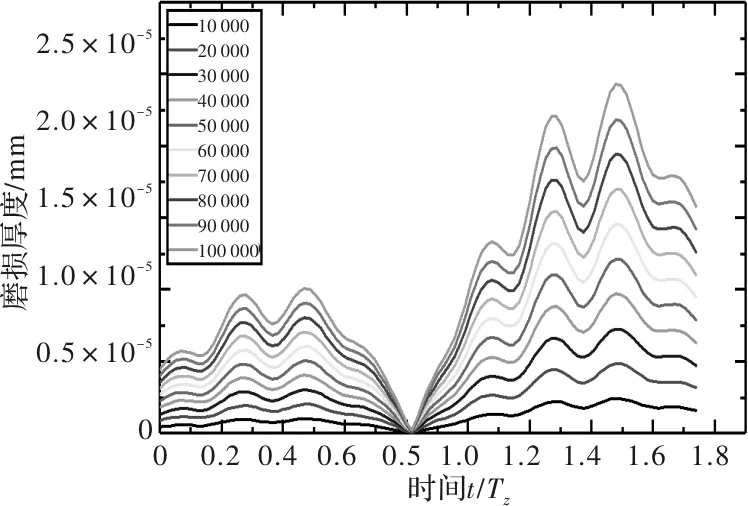
图7 10 r/min时主动轮齿面磨损分布

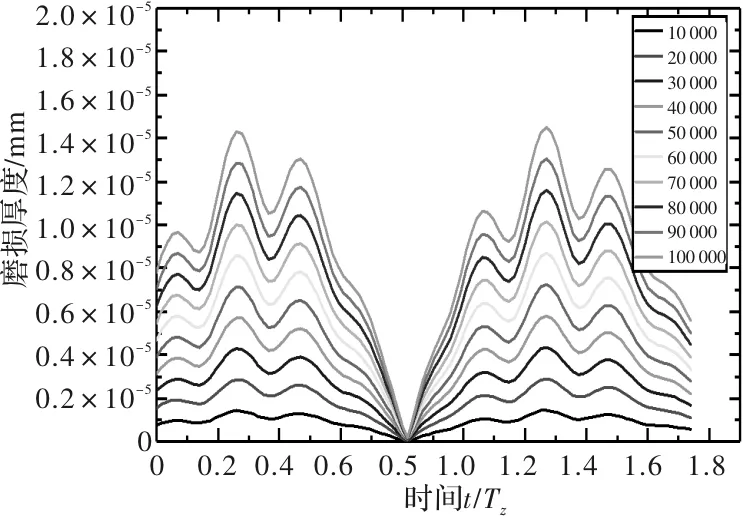
图8 10 r/min时从动轮齿面磨损分布

图9 30 r/min时从动轮齿面磨损分布

图10 30 r/min时从动轮齿面磨损分布

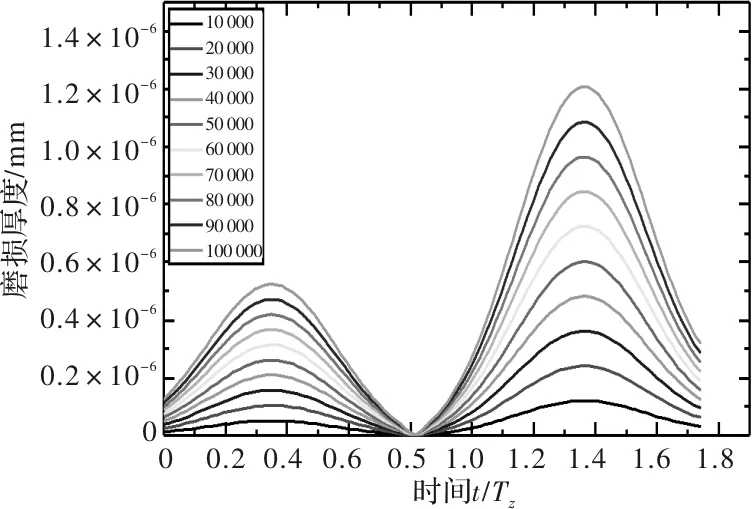
图11 10 r/min时从动轮齿面磨损分布

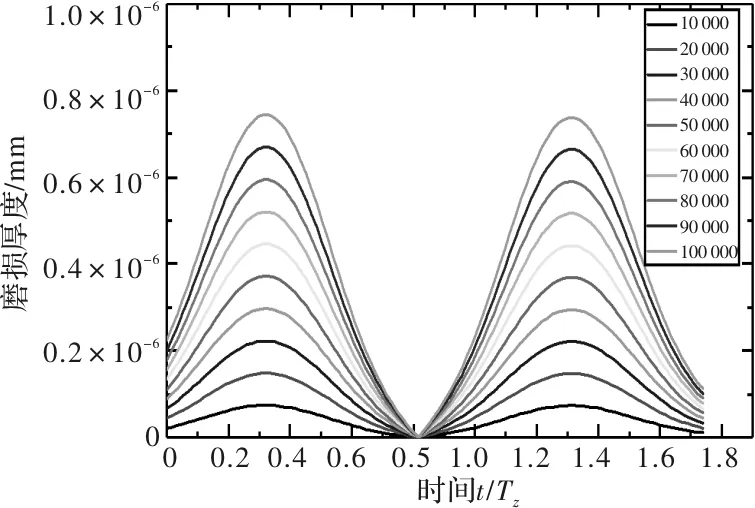
图12 10 r/min时从动轮齿面磨损分布

从图7～图12中可以看出，主动轮在进入啮合段时的磨损较退出啮合段有明显减少，同时从动轮在进入和退出啮合段的磨损较为均衡。且主动轮最大磨损较从动轮增加约67%。同时在功率不变时，随着转速增加，齿轮表面磨损逐渐平缓，齿轮齿面磨损量减少。

王晓笋等人则基于齿轮准静态条件计算齿轮齿面磨损分布，具体如图13～图18所示[12]。

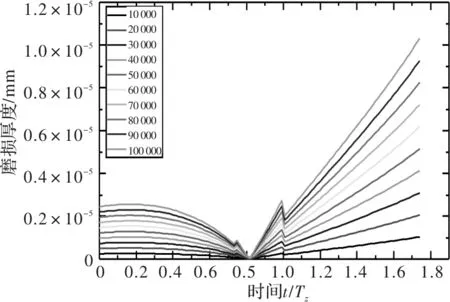
图13 准静态条件下10 r/min时主动轮磨损厚度

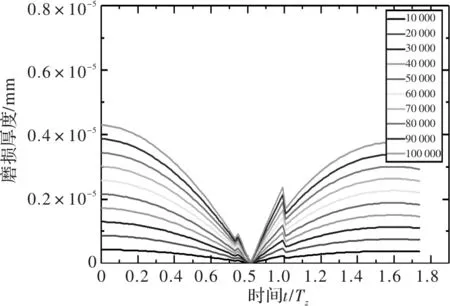
图14 准静态条件下10 r/min时从动轮磨损厚度

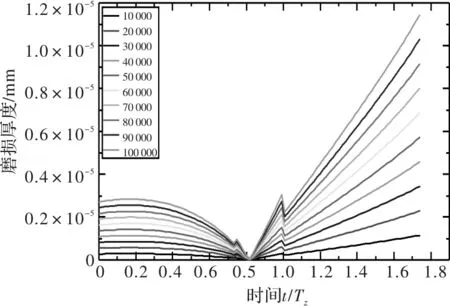
图15 准静态条件下30 r/min时主动轮磨损厚度

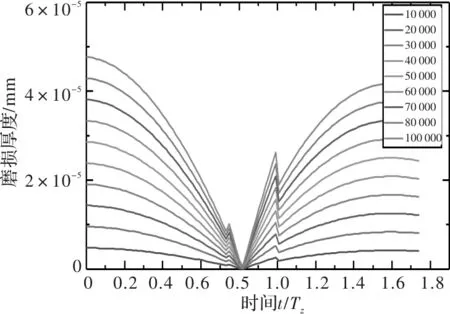
图16 准静态条件下30 r/min时主动轮磨损厚度

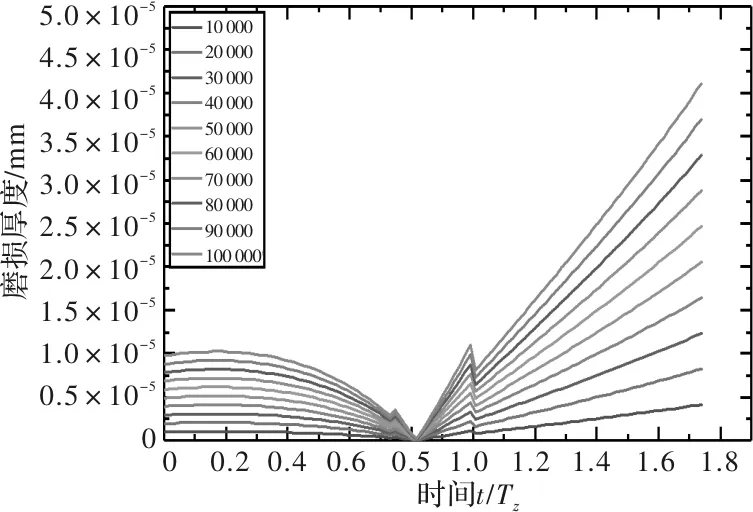
图17 准静态条件下50 r/min时主动轮磨损厚度

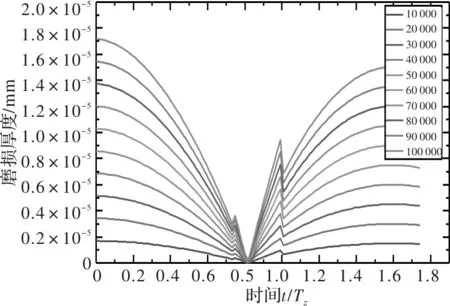
图18 准静态条件下50 r/min时主动轮磨损厚度

图13～图18中分别给出了主动轮和从动轮在10 r/min、30 r/min和50 r/min转速下，啮合次数分别为10 000，20 000，…，100 000时的齿面磨损厚度。可以看出，王晓笋等人计算齿面磨损分布时，在节线处齿轮磨损厚度同样为零，齿面磨损厚度随着齿轮节线距离增加而增加，但是在齿轮啮合力突变处能看出有明显突变。从动轮在进入啮合段的磨损较大，而主动轮在进入与退出啮合段的磨损较为均衡。可以看出准静态齿轮齿面磨损计算无法反映出齿轮的动态特性。

5 结论

本文利用Archard粘着磨损理论，并结合最小势能理论计算低速重载齿轮在转速变化时的齿轮齿面啮合力变化规律，同时计算出在变载荷条件下的齿轮磨损厚度变化。随着转速升高，齿轮齿面动态啮合力逐渐趋于平稳，齿面冲击减弱。通过对比准静态齿轮齿面磨损计算方法，可以看出需要充分结合齿轮的动态特性并计算齿面磨损分布，齿轮齿面动态啮合力变化是导致齿齿面磨损分布变化的主要原因。