基于轨道动力学特性的小天体物理参数感知方法

罗 燕，秦 同，乔 栋

（1. 北京理工大学宇航学院，北京100081；2. 清华大学精仪系，北京100084）

1 引 言

小天体是太阳系中较古老的一类天体，探测小天体，获取其物理参数，是研究太阳系形成与演化、生命起源与进化，以及抵御外来天体撞击的重要技术途径，是人类探索和开发宇宙资源的重要技术手段。同时，也为试验验证空间技术，尤其是深空探测技术提供了平台。目前，小天体物理参数的获取方式主要包括近距离光学成像、多谱段光谱测量和表面采样探测。此类方式可以感知小天体的尺寸、形状、自旋等物理参数，以及小天体表面地形、地表物质组成等。但光学观测的方式精度较低，且无法获得小天体内部质量与密度分布等信息。小天体的引力场以及自旋参数是小天体探测的基本内容之一。感知高精度的小天体引力场以及自旋，特别是不规则形状小天体引力场与自旋，有助于探索小天体的内部结构、质量与密度分布等信息，揭示小天体起源，获得新的科学发现。

小天体引力场以及自旋信息的获取通常有两种方式。其一，从传统的光学观测中提取光度或光学特征点等有效信息，以此为观测量反演自旋角速度以及外部形貌［1-2］，在均匀密度的假设下，获得质量分布，从而建立引力场模型［3-5］。由于这类方法的信息源来自小天体表面光学观测，因此获得的自旋角速度信息以及引力场模型较为粗糙，且无法体现小天体内部结构与质量信息。另一种方法是通过探测器轨道数据进行反演。未来的探测器需具有全面的感知能力，包括环境感知及自身状态感知［6-7］。由于探测器的运动由其轨道动力学环境，即探测器所处引力场决定，且小天体自旋会影响引力场的空间分布，因此借助精确的轨道数据，可对小天体引力场与自旋进行精确感知［8］。NEAR 探测器在对Eros 433 小行星的近距离飞越过程中，通过地面的无线电测量与星载光学测量数据不仅实现了高精度定轨［9］，同时还对Eros 433 的引力场进行了估计，并在美国国家航空航天局官网公布了引力场球谐系数模型的前8 阶球谐系数，是通过轨道数据感知小天体引力场的先例。

高精度测量与动力学估计是感知小天体自旋角速度与引力场模型的前提。现阶段，对小天体探测器的测量主要为地面无线电测量，包括测距、测速、甚长基线干涉测量，以及星载光学相机测视线与激光测距仪测距［10-12］。综合各类测量信息，结合较粗糙的先验引力场模型，可以估计探测器在小天体坐标系的轨道。然而，地面测控定轨自主性差、精度随距离增加而降低、且测量几何构型变化弱，无法实现小天体坐标系下的精密定轨。此外，小天体自旋与引力场感知需要长时间连续测量估计，依靠地面测控成本高昂。光学测量虽自主性强，但受光学导航原理（图像特征提取与匹配）的限制，参数估计精度较低。因此，传统的测量定轨方式在定轨精度上只能满足工程需求，无法满足高精度引力场与自旋参数感知的需求。

本文针对无人系统在小天体科学探测方面的应用，研究基于轨道动力学特性的小天体引力场与自旋角速度感知问题，即如何通过小天体探测器之间的器间测距信息对小天体引力场模型参数与自旋角速度进行修正。该问题本质上为参数估计问题，可用的测量信息为器间测距，需估计的参数为引力场模型参数、自旋角速度以及探测器轨道。在二体动力学问题中，由于引力场的对称性，器间相对测量仅能确定探测器轨道的大小、形状与尺寸，但星座的旋转方位信息，即各个轨道升交点赤经、轨道倾角以及近地点幅角均不可估计［13-14］。原因在于，星座整体旋转时，器间的测距、测速信息不会发生变化，导致器间测量导航系统不完全可观。但在小天体的不规则引力场中，引力场各向差异显著，不再呈现对称性，因此星座旋转后，各轨道的大小、形状尺寸也会随之改变，从而引起器间测量的变化。如此一来，器间测量对轨道各个元素均有一定的敏感性，整个星座定轨系统完全可观。因此，小天体引力场的不规则性虽然增加了小天体附近轨道设计难度，但也由于其复杂性，改善了参数感知系统的可观性，是参数感知的有利因素。

小天体的不规则引力场是实现参数感知的关键因素，同时，由于先验引力场模型以及自旋角速度存在误差，在进行定轨估计时，除了各轨道状态，还需要将引力场模型系数以及自旋角速度作为待估状态变量进行估计。因此，基于动力学的小天体参数感知实质上为动力学参数估计。以小天体球谐系数模型为例，通过三维建模与均匀密度假设得到的引力场模型中各阶球谐系数误差较大，将各阶球谐系数以及自旋角速度作为状态变量，扩充至动力学估计系统的状态向量中，依靠器间观测量，通过非线性滤波算法同时估计各阶球谐系数、自旋角速度以及探测器轨道参数。

2 小天体附近探测器轨道动力学

2.1 小天体引力场模型

小行星形状不规则，内部密度的分布也不均匀，这使得中心天体对环绕飞行器的引力作用也不严格等于等效的质心引力，而是等于中心天体各部分质量引力作用之和，即引力位函数：

其中，r为飞行器的位置，s为小天体内某一点的位置，上述积分应该对整个中心天体体积进行积分，中心天体对环绕飞行器的引力可表示为：

由于我们无法得到精确的中心天体的质量分布结果，所以上式并不能用来计算中心天体的引力势。常用的中心天体引力的计算模型有球谐系数模型［15］、多面体模型［16］、质点群模型等［17］。本文用球谐函数的级数展开式表示小行星的引力势能，能够更直观地描述小天体模型精度阶次。球谐系数模型如式（3）所示，小行星引力向量可以通过对势能求梯度得到。

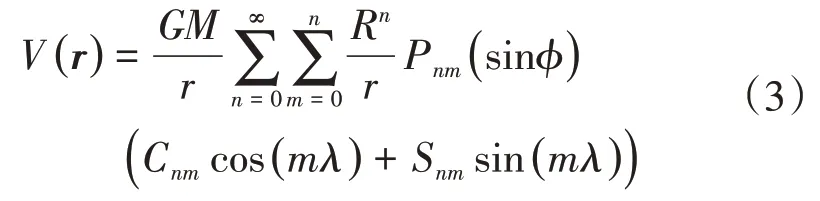
其中：

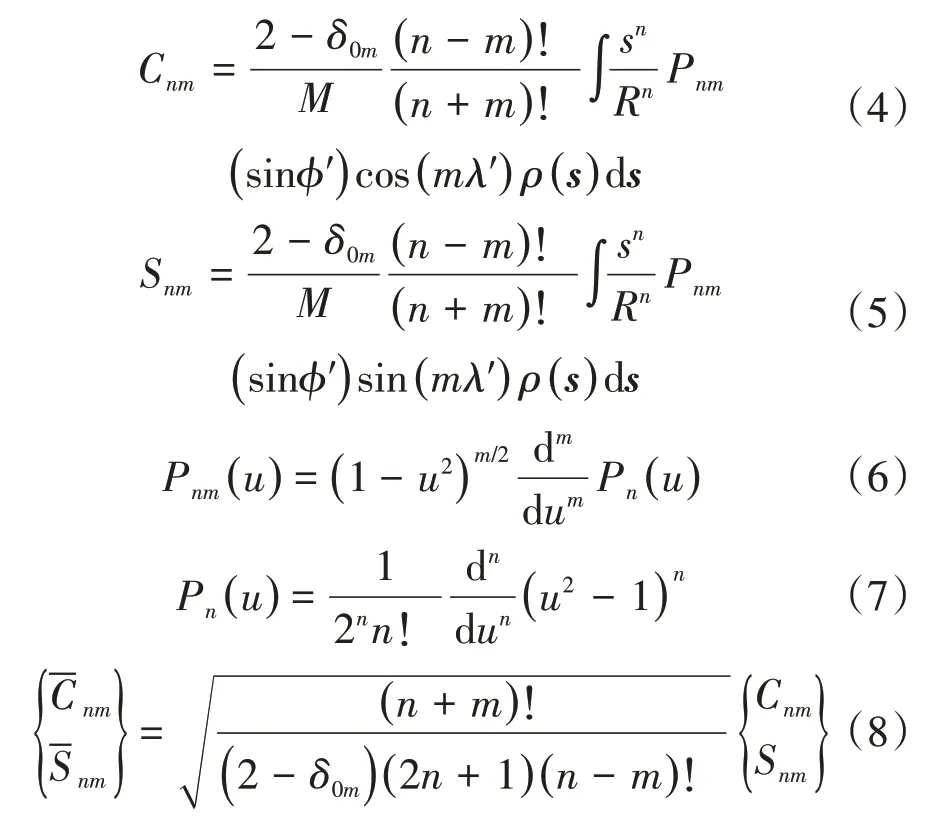
其中，φ和λ分别为飞行器在小天体固连坐标系下的纬度和经度，φ′和λ′分别为积分单元的纬度和经度，Cnm和Snm为非归一化的引力场模型谐函数和为归一化的引力场模型谐函数。Pnm为勒让德多项式，δnm为克罗内克符号（即n，m相同为1，不同为0），GM为引力常数，R为天体平均半径。

由于Cnm和Snm的计算同样需要知道质量分布，故一般也无法计算。目前而言，谐函数和一般是发射卫星并通过定轨来获得，从而通过换算得到Cnm和Snm。

m=n= 0的项为中心天体的质心引力部分，当n，m不为0 时，代表中心天体引力位偏离中心质点的程度。

2.2 小天体附近探测器轨道动力学模型

在小天体固连坐标系下，探测器轨道动力学模型如式（9）所示：

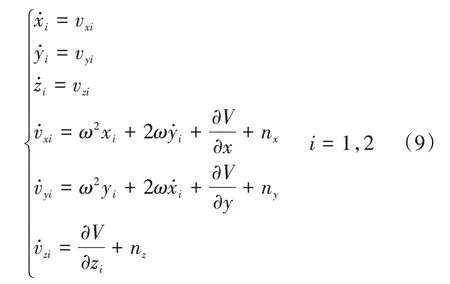
式中，xi，yi，zi为探测器i的三轴位置，ω为小天体的自旋角速度，nx，ny为未建模的干扰加速度，V为小天体的引力位势函数球谐系数模型。

3 引力场与自旋参数感知系统

3.1 系统状态模型

在小天体固连坐标系下建立引力场与自旋感知系统，待估系统变量为两环绕探测器的位置、速度、引力场球谐系数、模型系数，以及自旋角速度，系统状态变量如式（10）所示：

小天体各级引力场参数以及自旋角速度视为常数，其状态模型如式（11）所示：

由式（10）～（11）可得到引力场反演的系统状态模型如式（12）所示：

f(X)的具体表达式参照式（10）～（11）。

在两探测器绕飞小天体的过程中，通过器间特高频频段无线电通信，实现相对距离测量，测量模型如式（13）所示：

式中，wρ为测量噪声，在此假设为高斯白噪声。

3.2 系统状态估计方法

针对小天体引力场反演这一非线性估计问题，采用无迹卡尔曼滤波算法实现状态最优估计，给出tk时刻的系统先验状态Xk和状态误差协方差矩阵Pk，后续的估计流程如下：

（1）计算2n+ 1个sigma点及其权值。

式中，λ=α2(n+k)-n，α决定sigma 点的散布程度，通常取一个小的正值，k通常取0，β用来描述系统状态的分析信息，高斯分布情况下，β最优取值为2。

（2）计算sigma 点通过非线性函数f(X)的传播结果。

进而可得：

（3）观测更新。

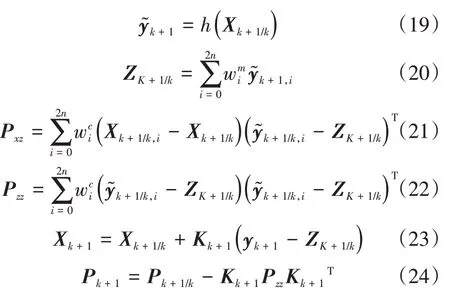
4 仿真结果及分析

对目标小行星2016HO3 进行引力场与自旋参数感知仿真分析，假设目标天体等效半径50m，密度1.26×103kg/m3（标准C 类小行星密度，2016HO3富含铁质，实际密度要大），套用Bennu 的不规则引力场模型，前四阶引力场参考模型参数如表1 所示。假设先验引力场各阶模型误差为50%，两探测器在本体系下的初始位置误差标准差为10m，器间测距精度为10cm/1cm，探测器绕飞高度1km/500m/100m。

表1 前八阶引力场参考模型参数Table 1 The first 8th order gravity model parameters

当测量精度为10cm 时，不同轨道高度的引力场反演仿真结果如图1 所示。轨道高度1km 时，通过240h（包含不可见弧段时长）的测量，可以反演出二阶引力场，轨道500m时，通过120h观测可以反演出三阶引力场，轨道高度100m时，通过240h观测可以反演出四阶引力场。不同轨道高度下探测器位置收敛精度近似，三轴位置精度约为20cm，如图2所示。

图1 测量精度10cm时不同轨道高度下感知的引力场模型参数误差Fig.1 The gravity parameter errors with 10cm measurement accuracy in situations with different orbits

图2 测量精度10cm时探测器轨道确定精度Fig.2 The orbit determination errors with 10cm measurement accuracy

考虑到2016HO3 的半径约为50m，因此100m轨道高度已接近工程可实现的极限最低高度。为反演更高阶次的引力场模型，需进一步提高测量精度。当测量精度达到1cm 时，100m 高度的探测器器间测距反演引力场结果如图3 所示，对应的探测器轨道精度如图4 所示。从仿真结果可以看出，当测量精度提升后，引力场反演精度明显提高，在100m 轨道高度进行器间测量反演，可修正六阶引力场参数。同时，探测器的定轨精度也从20cm 提高至5cm。通过引力场参数计算得到的真实引力加速度与感知加速度仿真对比如图5所示。图6给出了自旋角速度的误差。假设光学观测获取的先验自旋角速度误差为1%，通过动力学感知方法，经过170h 连续观测后，自旋角速度误差降低至0.01%。

图3 测量精度1cm时100m轨道高度120h观测感知的引力场模型参数误差Fig.3 The gravity parameter errors with 1cm measurement accuracy and 100m-height orbit within 120h

5 结 论

图4 测量精度1cm时探测器轨道确定精度Fig. 4 The orbit determination errors with 1cm measurement accuracy

图5 小天体表面真实引力加速度与感知加速度对比Fig. 5 The comparion of real and perceived acceleration errors

图6 自旋角速度感知误差Fig. 6 The self-rotation speed error

本文研究了基于轨道动力学特性的小天体引力场与自旋角速度感知方法，利用两个小天体环绕探测器之间的无线电测距信息，可同时估计探测器在小天体固连坐标系下的轨道、各阶球谐系数模型参数以及小天体自旋角速度。影响引力场与自旋感知精度的因素主要包括探测器轨道高度和测量精度两方面。仿真结果验证了轨道高度越低，测量精度越高，可以感知的引力场阶次越高，自旋角速度精度越高。精确的引力场信息是实施小天体探测任务的重要保障，本文的研究对空间环境感知、小天体探测中的参数估计有重要参考价值，创新点在于以器间测距信息为输入对小天体的引力场进行了较为精确的估计，同时提高了探测器的定轨精度。但利用球谐系数计算小行星非球星引力存在着一定的缺点，小行星形状越不规则时误差越大，本文仅套用Bennu 的引力场模型进行了模拟仿真，后期可利用仿真或真实拍摄的图片初步估计小行星的形状，并采用更高阶的非线性估计方法，进一步验证该方法和提高对小行星引力场参数估计的精度。