多臂机旋转变速机构凸轮廓线建模与重构

肖志涛， 尹洪环， 于鸿彬2，， 蒋秀明2，， 邵宏宇

(1. 天津工业大学 电子与信息工程学院， 天津 300387； 2. 天津工业大学 天津市现代机电装备技术重点实验室， 天津 300387； 3. 天津工业大学 机械工程学院， 天津 300387； 4. 天津大学 机械工程学院， 天津 300072)

在纺织机械中，多臂机又称为“多臂提综装置”，是无梭织机上使用比较普遍的开口装置。多臂机必须具有良好的力学性能，以适应织机的高速生产[1]。旋转式电子多臂机是一种积极式多臂机。近年来，制造商已经展示出运行速度达1 200 r/min的多臂机，这使得在高速喷气织机和喷水织机上采用旋转式多臂机成为可能。提综机构是旋转式多臂机核心部分，其将电动机输入的匀速转动转化为提综臂的变速摆动，进而实现综框在竖直方向的变速上下运动[2]。提综机构的核心组件是旋转变速机构，旋转变速机构关键部件共轭凸轮直接影响综框的运动特性，影响织机的织造质量和效率，因此，对多臂机旋转变速机构凸轮廓线进行建模与重构的研究具有重要意义。

目前，针对多臂机旋转变速机构的研究，张远华等[3]建立了多臂机旋转变速机构三维模型，并进行了运动学仿真分析。沈毅等[4-5]针对GT421型旋转式电子多臂机提综机构进行研究，从运动学设计角度出发，对共轭凸轮外轮廓线的极坐标进行理论推导；对主轴和凸轮摆臂的相对停顿时间做了理论分析和计算；从静力学设计角度分析多臂机提综机构的运动机制，对多臂机主传动构件建立运动学模型，并进行了相关的运动学仿真研究。EREN等[6-7]通过讨论给定多臂机主轴的特定输出运动曲线，得出提综机构带动综框的运动特性，比较了多臂机偏心机构和旋转变速机构对综框运动特性的影响。以上研究为多臂机旋转变速机构的设计和分析奠定了重要基础。

以旋转变速机构为研究对象，基于测绘的凸轮轮廓线或者基于给定的主轴运动曲线，求解出综框的运动特性，并进行运动学仿真分析。同时，随着织机转速越来越高，多臂机的开发朝着高速、高效、高可靠性方向发展[8-10]。旋转变速机构作为旋转式多臂机提综机构的核心部件，深入研究其凸轮廓线数学模型的构建，根据织机工艺要求逆向求解凸轮廓线并针对凸轮廓线优化分析具有重要意义。目前针对凸轮轮廓设计，特别是减少振动，提高稳定性和延长使用寿命[11-12]等方面的研究主要有：STODDART等[13-14]建立了从动件振动幅度和凸轮速度之间的特征关系。MERMELSTEIN等[15]在满足必要的约束条件下，使用分段多项式来优化相应运动量参数。QIU等[16]使用B样条生成优化的运动曲线，同时依据多设计目标，包括控制残余振动等来优化凸轮廓线。NORTON等[17]对凸轮廓线设计和制造提供重要理论依据和指导。

为此，本文在分析提综机构运动原理，研究旋转变速机构凸轮廓线数学模型的构建方法基础上，建立基于综框运动特性的数值求解凸轮廓线方法，构建基于综框运动特性的凸轮廓线逆向求解系统，解决测绘凸轮廓线导致综框运动特性曲线不连续和不光滑的问题。在此基础上，对获得的非中心对称凸轮廓线运用粒子群算法[18-20]进行优化和重构，为旋转式多臂机整体性能的改善提供理论方法。

1 提综机构运动原理

提综机构包括多臂机旋转变速机构、多臂机偏心机构、运动传递机构和综框。旋转变速机构工作原理如图1所示。其中共轭凸轮(5和10)固定在多臂机箱体静止不动，凸轮摆臂(2和8)铰接在齿轮(1)上，并且可以绕其铰接点转动，从而将电机输入的匀速圆周运动通过齿轮(1)传递给凸轮滚子(3、6、9和12)，凸轮滚子沿着共轭凸轮(5和10)廓线运动，通过主轴连杆(4和7)将织机的匀速转动转换成主轴(11)的旋转变速运动。

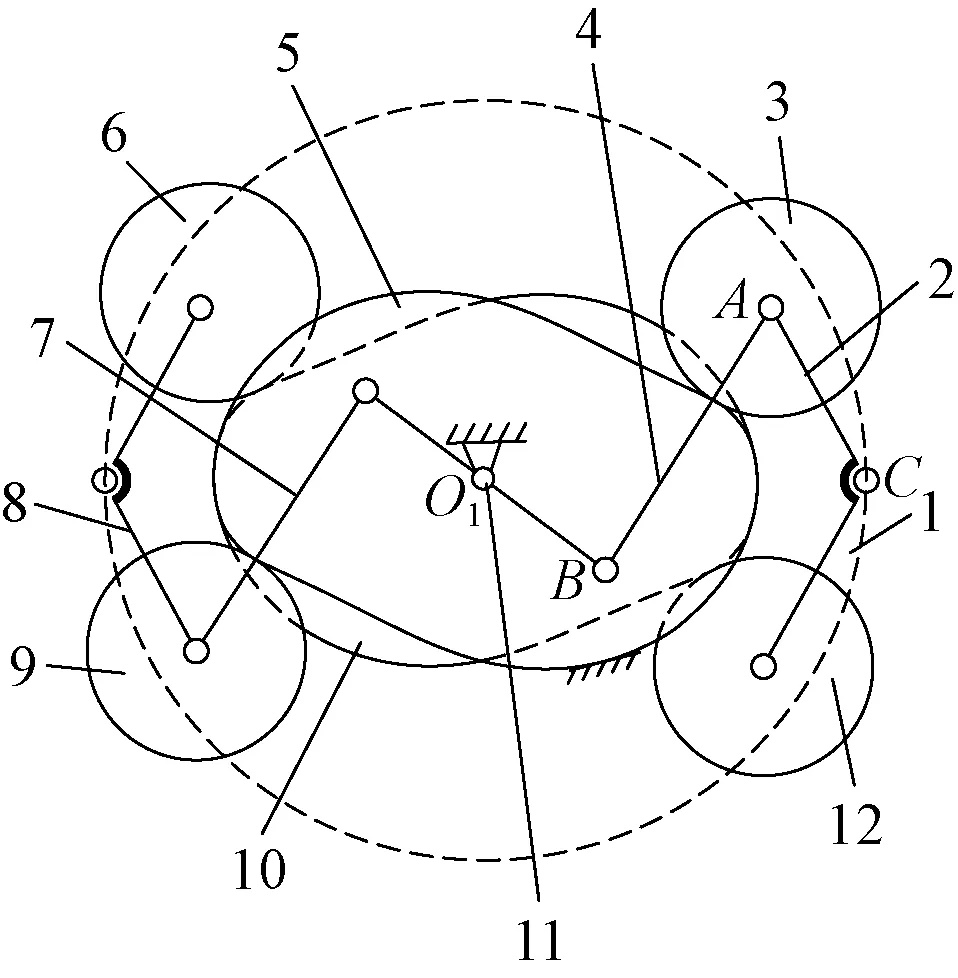
图1 旋转变速机构工作原理Fig.1 Working principle of modulator

偏心机构、运动传递机构和综框的工作原理如图2所示。

13—偏心盘凸轮；14—环形连杆；15—提综臂；16—提综臂连杆； 17—转臂；18—转臂连杆；19—综框连杆； 20—支撑连杆；21—综框。图2 偏心机构、运动传递机构和综框工作原理Fig.2 Working principle of eccentric mechanism, motion transmission mechanism and heald frame

偏心机构由偏心盘凸轮、环形连杆、提综臂组成。偏心盘凸轮，因其旋转中心与其几何中心不同，故偏心机构等效机构为曲柄摇杆机构(O1DEO2)。当旋转变速机构的齿轮转动时，主轴的旋转变速运动传递到提综臂,实现提综臂的上下摆动。运动传递机构包括提综臂连杆、转臂、转臂连杆、综框连杆、支撑连杆，其等效机构是四连杆机构(O2FGO3)和曲柄滑块机构(O3HI)，提综臂的摆动通过运动传递机构传递给综框，实现综框的上下变速运动。

2 旋转变速机构凸轮廓线建模

在织机织造过程中，综框带动经纱，决定了经纱的运动特性。为保证平稳的经纱织造过程，综框在运动中，要求速度平稳无突变，综框从静止到运动和从运动到静止的过渡要缓慢，同时要求尽量降低加速度以减小对经纱的冲击。目前常用的测绘方式得到的凸轮廓线，会导致综框在速度、加速度和跃度上存在明显的波动及跳跃现象。

为解决凸轮廓线产生的上述问题，采用指定综框运动特性逆向求解凸轮廓线方法。由于11次多项式[21]满足位移、速度、加速度和跃度连续，并且加速度较低，较接近综框的运动特性，因此，初步确立该11次多项式作为综框运动位移函数，进而基于综框运动特性的数学表达，建立逆向求解凸轮廓线的数学模型。

2.1 偏心机构、运动传递机构和综框建模

图3示出多臂机偏心机构、运动传递机构和综框简图，连杆O3G与曲柄O3H刚性连接，其夹角φ9绕O3旋转，曲柄O3H与X轴正向夹角为φ10。

图3 偏心机构、运动传递机构和综框简图Fig.3 Schematic diagram of eccentric mechanism, motion transmission mechanism and heald frame

L(u)为综框以多臂机齿轮转角θ为变量的位移函数，定义为L(u)=S(u)+S0，其中，u=θ/β，0°≤θ≤180°，β=180°；S0为综框重心I到X轴的距离；S(u)为该11次多项式，方程表达式如下：

S(u)=h(336u5-1 890u6+4 740u7-

6 615u8+5 320u9-2 310u10+420u11)

(1)

式中，h为综框的升程。

在图3中设笛卡尔直角坐标系(X,Y),以中心点O1作为坐标原点，

设：

F1(e,lHI,lO3H,L(u),φ10)=0

(2)

有：

(3)

则：

(4)

式中，偏心距e、lO3H和lHI为曲柄滑块机构(O3HI)中的已知参数。

在运动传递机构的四连杆机构(O2FGO3)中，由几何关系可知：

(5)

设：

F2(lO2O3,lO3G,lFG,lO2F,φ8,φ6)=0

(6)

则：

(7)

式中：lO2O3,lO3G,lFG,lO2F,φ9为已知参数，φ10可由式(4)求得，φ8=φ9+φ10。

由式(7)解得：

(8)

(9)

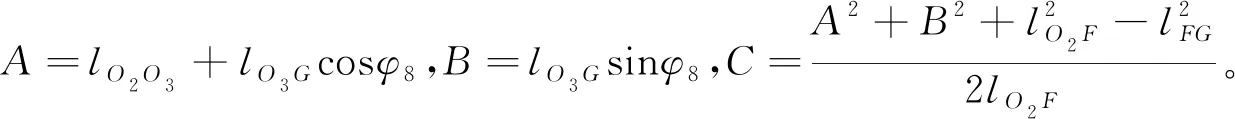
根据运动原理知输出角φ2可由角φ4求得。

由几何关系可知：

(10)

设：

F3(lO1O2,lO2E,lDE,lO1D,φ4,φ2)=0

(11)

则：

(12)

式中：lO1O2,lO2E,lDE,lO1D,φ5为已知参数；φ6可由公式(9)求得，且满足φ4=φ5+φ6。

由公式(12)解得：

(14)

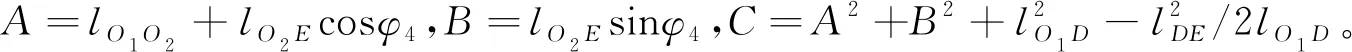
2.2 旋转变速机构凸轮廓线建模

图4示出旋转变速机构简图。齿轮的旋转角为θ,ω为齿轮的角速度，φ1为旋转变速机构主轴旋转角度，φ2是偏心盘凸轮的旋转角度，φ2可从式(14)获得。结合φ1运动规律，建立旋转变速机构凸轮廓线求解模型。

图4 旋转变速机构简图Fig.4 Schematic diagram of modulator

根据几何关系有：

(15)

求得凸轮理论廓线上任意点A的坐标：

(16)

yA=(C-Ax)/B

(17)

A1=A2+B2

B1=2AByB-2AC-2B2xB

xB=lO1Bcosφ1

yB=lO1Bsinφ1

xC=lO1Ccosθ

yC=lO1Csinθ

对于多臂机旋转变速机构，凸轮实际廓线与理论廓线法线方向的距离等于滚子半径r，沿凸轮理论廓线任意点A的法线方向取距离r，可获得凸轮实际廓线上相应点坐标T(xT,yT)，过凸轮理论廓线上A点处法线n-n的斜率为：

(18)

式中，γ为法线n-n与x轴夹角。

根据公式(18)可得：

(19)

根据公式(15)～(19)可以求出凸轮实际廓线上相应点T坐标：

(20)

至此，根据综框的多项式运动特性，完成了多臂机旋转变速机构凸轮廓线建模，同时获得了多臂机提综机构各杆件的运动特性与齿轮旋转角度之间的关系。

3 旋转变速机构凸轮廓线求解

设定多臂机提综机构的物理参数和几何尺寸如表1所示。

表1 提综机构的物理参数和几何尺寸Tab.1 Physical parameters and geometric dimensions of shedding mechanism

利用公式(1)～(20)，采用Microsoft Visual Studio VB.NET编程进行数值计算，逆向求解获得凸轮廓线如图5所示。由于多臂机偏心机构是无急回特性的曲柄摇杆机构，去程和回程的运动特性不同，因而获得对应于去程和回程的凸轮廓线也不同。其中曲线S1为偏心机构(见图3)连杆O1D从D0点逆时针运动到D1点形成的半段凸轮廓线，曲线S2为连杆O1D从D0点顺时针运动到D1点形成的另半段凸轮廓线，由曲线S1和S2形成的完整凸轮廓线并非中心对称。为了直观获得非中心对称程度，将曲线S1沿O1点顺时针旋转180°形成曲线S1′，与曲线S2比较可知非中心对称程度。

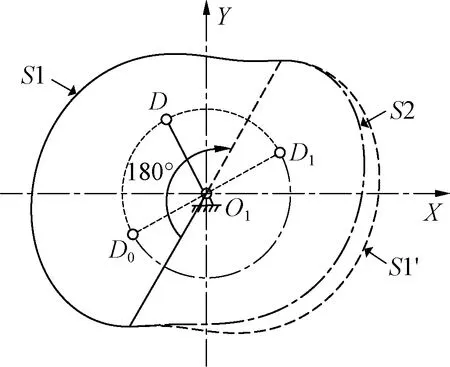
图5 逆向求解获得凸轮廓线Fig.5 Conversely obtained cam profiles.

根据曲线S1和S2形成的非中心对称凸轮廓线及表1中各构件参数，运用SolidWorks软件建立提综机构数字样机，通过SolidWorks Motion进行运动仿真分析，获得齿轮旋转1个周期内综框的无量纲运动特性。图6示出综框归一化的位移、无量纲速度、无量纲加速度和无量纲跃度曲线，其中归一化幅值为106.8 mm，同时示出11次多项式曲线。

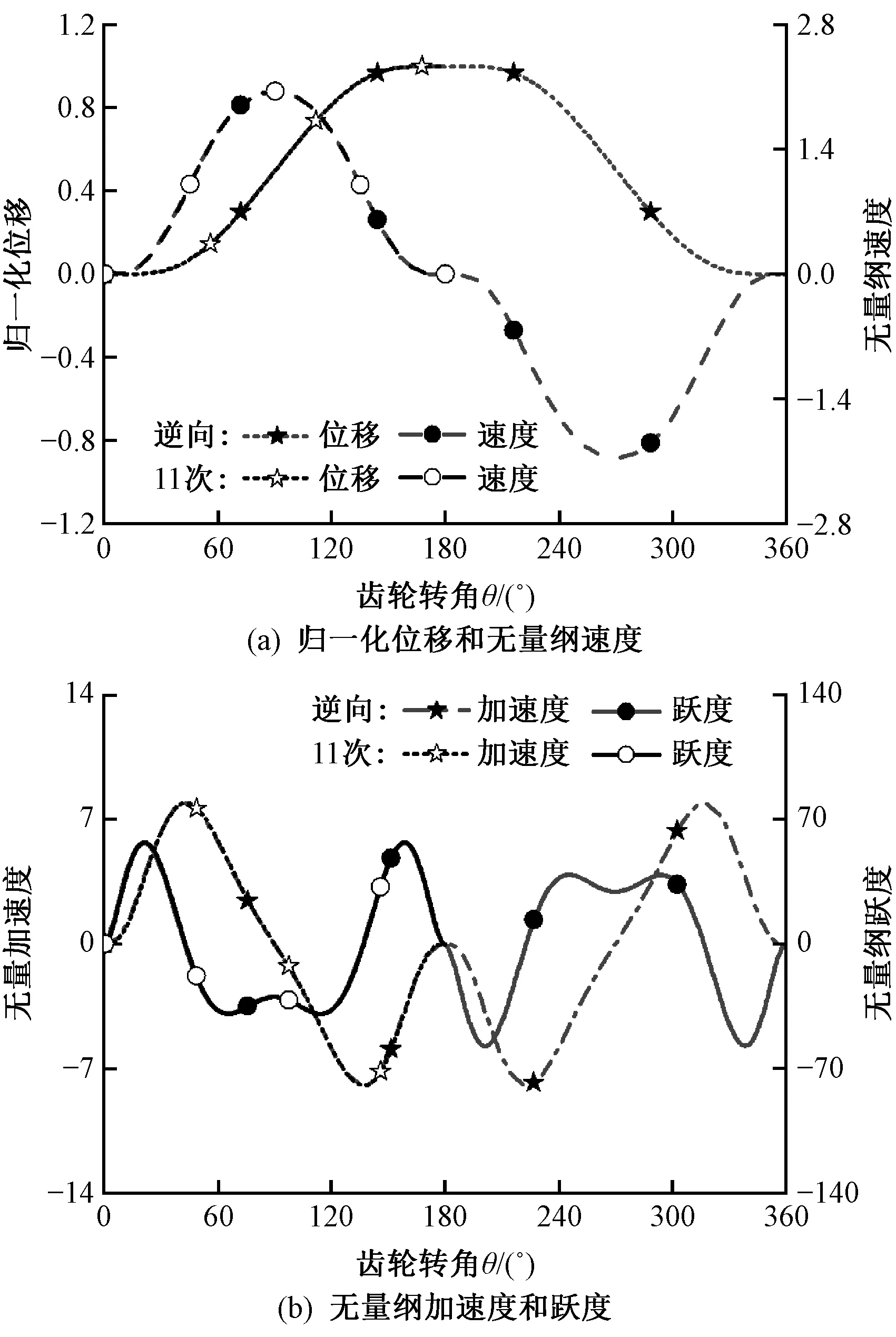
图6 非中心对称凸轮产生的综框 运动特性与11次曲线比较Fig.6 Comparison of heald frame motion characteristics generated by noncentral symmetrical cam and 11th curves.(a) Normalized displacement and dimensionless velocity;(b) Dimensionless acceleration and jerk

将图6中黑色曲线(11次多项式曲线)与灰色曲线(逆向求解获得凸轮产生的综框运动特性)对比结果表明，在齿轮旋转半个周期内求解的综框运动特性与11次多项式曲线完全相同，验证了所建立的逆向求解凸轮廓线模型的正确性。通过对图6分析可知，综框在上升段和下降段产生的综框运动特性相同，并且齿轮正转和反转产生的综框运动特性也相同。但是，由于多臂机旋转变速机构中的凸轮是共轭凸轮，上述获得凸轮廓线并非中心对称，因此拟采用粒子群算法重构凸轮廓线，使得凸轮廓线基本中心对称，同时符合综框的运动特性。

4 旋转变速机构凸轮廓线重构

4.1 粒子群优化算法

针对凸轮廓线优化问题，粒子群算法[22-23]数学描述为：在由N个粒子组成的三维搜索空间中，第i个粒子的位置可表示为：xi=(xia,xib,xic)，运动搜索到的最优位置是Pi=(pia,pib,pic)，xi(t)为第i个粒子在t时刻的位置，粒子速度vi=(via,vib,vic)，vi(t)为第i个粒子在t时刻的速度，群体中全部粒子迄今搜索到的最优位置为pg=(pga,pgb,pgc)，对于每一次迭代，其第d维按以下方程进化：

vid(t+1)=vid(t)+cp×r1×[pi(t)-xi(t)]+

cg×r2×[pg(t)-xi(t)]

(21)

式中：t为当前时刻；cp，cg为学习因子，为非负常数，用来调节粒子飞行的步长；r1和r2为属于[0，1]的随机数。

粒子群算法的流程如下：

1)设定学习因子cp和cg，最大迭代次数MaxDT，将当前进化时刻设置为t=1，在定义空间Rn中随机获得N个粒子，组成初始粒子群，并设定粒子的初始位置与速度；

2)分别对每个粒子计算目标函数值来评价其适应值；

3)比较每个粒子当前适应值与迄今搜索到的个体历史最优值pi，如果优于pi，则将其作为pi；

4)比较每个粒子当前适应值与群体历史最优值pg，如果优于pg，则更新当前全局最优值；

5)根据公式更新每个粒子的飞行速度和位置；

6)若满足终止条件，则终止迭代，否则返回步骤2)。

终止条件为：

1)达到最大迭代次数；

2)已获得足够好的适应值；

3)最优解停滞不再变化。

4.2 基于粒子群算法的凸轮廓线重构

在图5中，取t时刻凸轮廓线S2(t)上1 000个均布点坐标定义为(xti,yti)，取t时刻凸轮廓线S1′(t)上1 000个均布点坐标定义为(mti,nti)，对应点的欧式距离之和设为ρ(t)，用以表征2个凸轮廓线的非对称度。则有：

(22)

式中，i=1,2,…,1 000。

目标函数：

Minρ(t)

(23)

边界条件：

a+b+c=1

(24)

修正函数：

(25)

利用粒子群算法对凸轮廓线进行重构求解，并用编程工具对以上数学模型编程计算，取粒子群的规模为100[24]，设定最大迭代次数为5 000，依据经验值范围[18-20]和粒子收敛速度试算后，确定学习因子cp=0.05和cg=0.1。当迭代次数超过1 800次后，最优解停滞不动，获得粒子收敛的群体行为在图7中示出。

图7 粒子收敛的群体行为Fig.7 Swam behavior of convergence. (a) Initial state;(b)500 iterations; (c) 1 000 iterations; (d) 5 000 iterations

图7中黑色粒子为最优粒子，示出了粒子初始分布情况、粒子经500次、1 000次和5 000次迭代后收敛情况。可以看到粒子收敛情况较好，同时得出修正系数与目标函数结果如表2所示。

表2 修正系数与目标函数结果Tab.2 Correction factor and objective function result

结果表明，经优化后获得修正系数：a=0.970，b=0.543，c=-0.513，目标函数值为31.51，得出重构后凸轮廓线。图8示出重构前后凸轮廓线比较。廓线S1和S2是重构前获得的凸轮廓线，廓线S3和S4为经过粒子群算法优化重构后获得的凸轮廓线。为了将重构前后的凸轮廓线进行对比，将廓线S1和S3沿O1点顺时针旋转180°形成廓线S1′与S3′，与廓线S2和S4比较，可以看到重构后的2个半段凸轮廓线S3和S4基本中心对称，结果表明，经粒子群算法优化重构后目标函数值由优化前的25 727.20下降到31.51，使得凸轮廓线中心对称度提高了99.878%。

图8 重构前后凸轮廓线比较Fig.8 Comparison of cam profiles before and after reconstruction

根据由廓线S3和S4形成的重构后廓线构建凸轮三维模型，将其安装到提综机构数字样机中，运用仿真软件进行运动仿真分析，获得齿轮旋转1个周期内综框的运动特性。图9示出综框运动特性归一化结果，同时示出测绘与重构凸轮产生的综框运动特性比较。

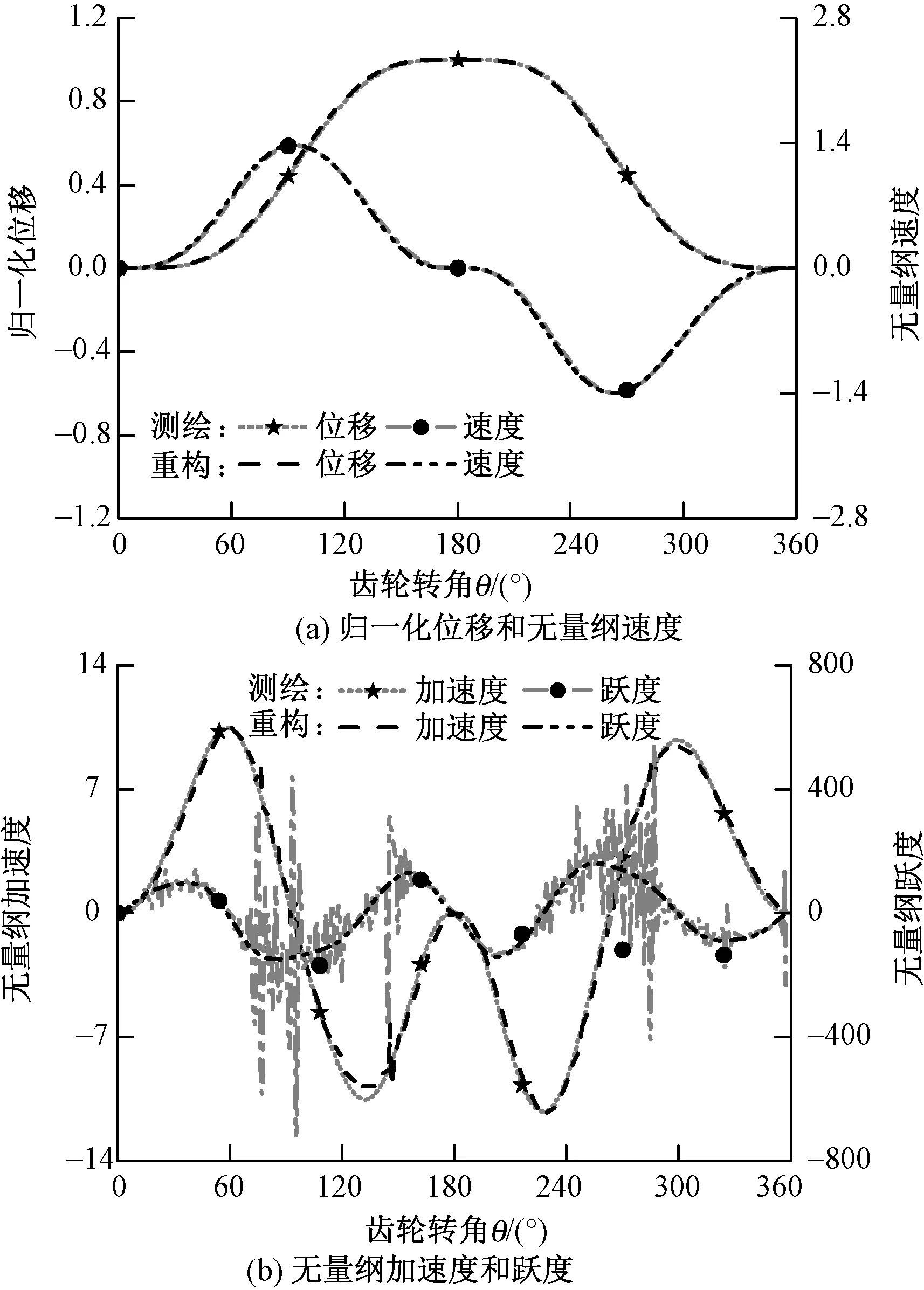
图9 重构与测绘凸轮产生的综框运动特性比较Fig.9 Comparison of heald frame motion characteristics generated by reconstruction and mapping cam. (a) Normalized displacement and dimensionless velocity; (b) Dimensionless acceleration and jerk

将优化重构后凸轮产生的综框运动特性与测绘凸轮产生的综框运动特性比较分析，可看出：经过粒子群算法优化重构后的凸轮产生的综框运动特性在上升段和下降段相同，并且齿轮正反转产生的综框运动特性也相同。同时发现获得的综框运动特性平滑无波动，改善了测绘得到的凸轮廓线导致综框运动特性在速度、加速度和跃度上存在的波动及跳跃现象。表明基于粒子群算法进行凸轮廓线重构，获得的凸轮提高了多臂机整体运动学性能。

5 结 论

1)根据综框运动特性的多项式数学表达，构建了求解多臂机旋转变速机构凸轮廓线数学模型，列出了凸轮廓线求解方程，并用Microsoft Visual Studio VB.NET编程计算，获得了求解后的凸轮廓线，建立了凸轮廓线逆向分析系统。运用SolidWorks仿真软件建立了提综机构的数字样机模型，并将数值计算得到的凸轮廓线进行仿真分析，求解了综框运动特性，分析了综框运动特性的可靠性，验证了所建逆向求解凸轮廓线数学模型的正确性。

2)由于偏心机构是曲柄摇杆机构，导致求解的凸轮廓线并非中心对称。将求解获得的非中心对称凸轮廓线运用粒子群算法进行重构，获得优化重构后的凸轮廓线，使得凸轮廓线中心对称度提高了99.878%，同时获得修正后的综框运动特性数学表达。

3)重构后的凸轮廓线满足齿轮正反转旋转，综框运动特性完全相同的要求，同时，使得综框的位移、速度、加速度和跃度平滑无波动，改善了测绘得到的凸轮廓线导致综框在速度、加速度和跃度上存在的明显波动及跳跃现象，有效提升了多臂机的运动学性能。