基于数字单元法的三维正交织物微观几何结构建模

2021-01-05何田田王友棋

纺织学报 2020年7期

马莹，何田田，陈翔,3，禄盛,3，王友棋

(1. 重庆邮电大学先进制造工程学院，重庆 400065； 2. 堪萨斯州立大学复合材料实验室，堪萨斯 66506； 3. 西安交通大学机械结构强度与振动国家重点实验室，陕西西安 710049)

高性能纤维增强复合材料具有高比刚度、高比强度、抗冲击和耐疲劳等多种优异的力学性能，在航空航天、军事、医疗等诸多领域[1]得到广泛的应用。相比其他复合材料增强体而言，三维机织物具有多取向性、可设计性以及结构效能优异等特点，尤其在冲击吸能阻尼结构方面优势巨大，被广泛用于人体防弹衣等柔性防护装备。

目前已有众多学者应用多种建模软件对不同三维织物进行了细观结构建模，并从理论上分析其细观结构。王旭[2]应用动画渲染和制作软件3ds MAX(3D Studio Max)基于曲线控制点的纱线轴线生成方法，结合截面曲线放样技术建立了三维织物的细观模型；陈振等[3]将纱线假设为连续实体，讨论了织物几何结构建模软件TexGen的仿真建模方法及其结果的准确性。虽然该软件所建的特定几何模型与真实织物图像对比有一定的拟合度，但并不能很好反映所有类型织物的纱线形态。余育苗等[4]以三维正交机织复合材料为研究对象，假设纱线横截面为矩形截面，结合三维机织复合材料的结构特点建立了单胞模型。

上述建模方法较为真实地反映了三维织物细观几何结构，然而所建数值模型大都以纱线为最小单位，将纱线横截面理想化地假设为椭圆、跑道、凸透镜等形状；但实际织造过程中织物横截面是动态变化的，与假设的截面形状存在较大差异，因此，为了建立更加接近三维织物真实形态的数值模型，有学者在原有理想模型基础上提出了多种改进方法，Green等[5]建立了一种用于预测三维织物在织造和压实过程中变形情况的精确模型；Fredrik等[6]将纱线模拟为链式结构，在细观尺度上提出了一种管状编织物几何建模方法，该方法展现了光滑的纱线路径和截面形状变化；Isart等[7]分别通过将纱线截面形状理想化的建模方法、数字单元法和理论分析方法建立了织物几何模型，并分析评价了3种建模方法的优缺点。

三维机织物的几何结构与力学性能高度关联，研究其表征技术，对该类复合材料的有效利用和深层次开发具有重要工程实际意义。目前已有研究大都是参考织物截面显微图像假定其理想几何形状，然后在建模软件中进行参数设置并一步成型，不能有效反应织物内部复杂微观几何结构。因此，针对现有研究中假设纱线截面为理想形状建模的问题，本文采用由堪萨斯州立大学复合材料团队研发的纺织建模软件数字织物力学性能分析器(Digital Fabric Mechanics Analyzer，DFMATM)。该软件以数字单元法为理论基础，可实现三维机织物织造过程动态仿真及其微观几何结构数值模拟[8]，现已被业界广泛用于构建二维平纹、三维正交[9-10]、角联锁等复杂织物组织。与其他纺织建模软件相比，数字单元法在近似于纤维尺度建立了织物几何结构数值模型，规避了对纱线截面形状和材料弹性常数等的简化及假设，在时域中模拟了织造过程，能够真实反映纱线截面的动态变化。

本文以数字单元法为理论基础，通过分析该方法在织物织造行为模拟中的作用机制，提出了一种计算纤维间摩擦力的方法。进而研究了三维正交织物组织结构关键点位置，建立其拓扑结构，并在时域中对该织物的织造行为进行模拟，获得了5个精度递进的单胞数值模型。通过实验对比，分析了纤维间摩擦力对织物内部节点力和势能的影响，揭示了纱线纤维化离散程度对仿真时间、织物厚度、纤维体积分数和纱线空间构型的影响规律。

1 数字单元法建模原理

1.1 基本要素

数字单元法主要包括3个基本要素：数字纤维、数字纱线和接触单元，如图1所示。可以看出，数字纤维由节点和杆单元链接而成，节点与杆单元间无摩擦作用。当杆单元长度趋近于零时，数字纤维可灵活弯曲，可模拟出实际织物中纤维单丝的真实形态，并赋予其真实材料属性。数字纱线由多根数字纤维组成，数字纤维的数量由真实纱线所包含的纤维数量和组成符合真实纱线截面形状所需数字纤维数量共同决定。数字纱线通常包含10～100根数字纤维，数字纤维的排列方式决定了纱线的截面形状。在仿真过程中，当相邻纤维之间的间距小于数字纤维直径时，建立接触单元。

图1 数字单元法三要素Fig.1 Three elements of digital element approach. (a) Digital fiber; (b) Digital yarn; (c) Contact element

数字单元法仿真结果的准确性主要由网格划分精细程度决定，使用该方法进行织造过程的仿真，通过网格划分的纱线纤维化离散和纤维离散实现。在纱线纤维化离散中，1根纱线被离散为与原有纱线路径平行的多根数字纤维，且离散前后纱线截面积和所有数字纤维的截面积总和保持不变。在纤维离散中，组成数字纤维的杆单元长度减小，节点数量增加，且杆单元长度与数字纤维直径呈定比。在张力的作用下，因纱线纤维化离散产生的数字纤维间发生相对运动，纱线截面形状沿轴线方向发生变化。纤维离散保证了计算纤维间作用力的准确性，2种离散机制的共同作用实现了三维机织物微观尺度几何结构预测，因此，纱线中的数字纤维数量和杆单元长度是影响仿真结果准确性的重要因素。

1.2 纤维间的相互作用力

为了真实反映织物织造过程中纱线的受力情况和成型过程，数字单元法不断优化改进，在力学模型中先后加入了纱线张力、接触力[11]、阻尼力[12]与摩擦力。

纤维间的摩擦存在于整个织造过程中，摩擦力的计算方法影响了纱线的几何形状和织物势能，因此，依据纤维间的相互作用机制可建立其摩擦力计算模型。纤维间的摩擦力由节点的运动状态和接触单元间的相互作用力大小共同决定。摩擦力计算方法示意图如图2所示。

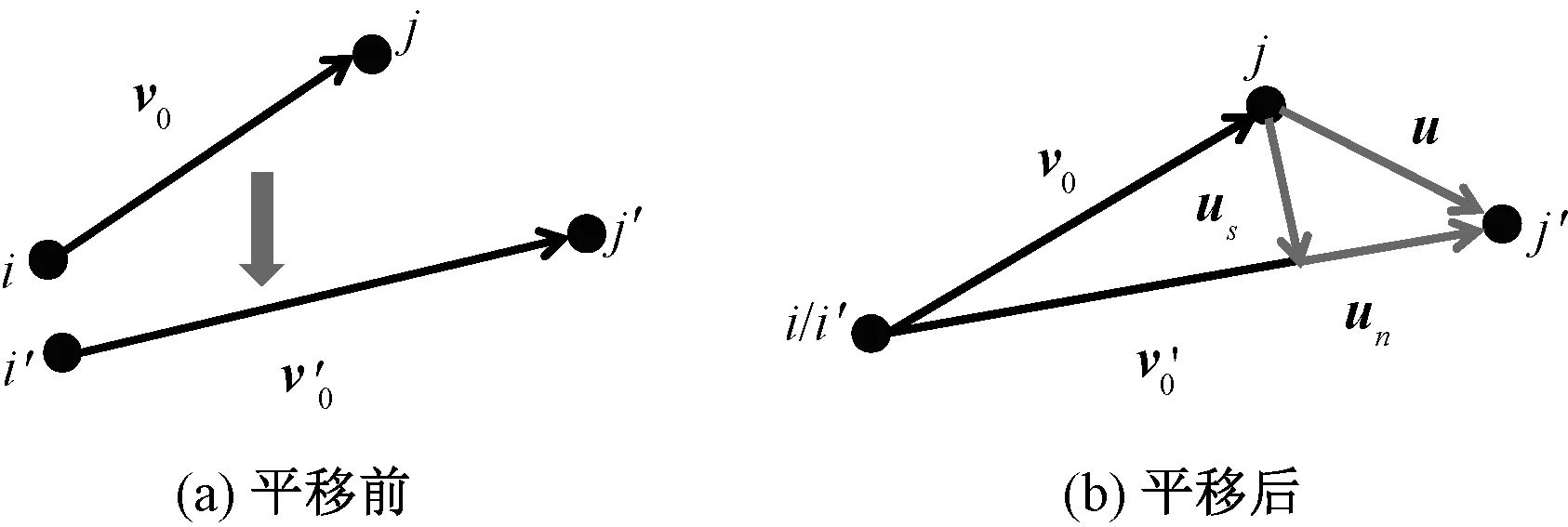
图2 摩擦力计算方法示意图Fig.2 Illustration of friction force calculation. (a) Before translation; (b) After translation

节点i和节点j组成1对接触单元，分别属于2根不同的纤维。平移前该接触单元所处的相对位置如图2(a)所示，从t时刻到t+1时刻，节点i和j分别移动到i′和j′位置。令ij为向量v0，i′j′为对应向量v′。令节点i和j在t时刻首次发生接触，并在t+1时刻仍然保持接触，则摩擦从t+1时刻开始计算。将向量ij平移到i′j′处，使点i与点i′重合，平移后的接触单元如图2(b)所示。令节点j相对节点i的相位移矢量为u；相对切向位移矢量为us；相对法向位移矢量为un。摩擦力可由式(1)、(2)计算得出。

Fs=ksus

(1)

ks=μkn

(2)

式中：Fs为纤维间摩擦力，N；ks为接触单元摩擦刚度，N/m；μ为摩擦因数；kn为接触单元法向摩擦刚度，N/m。

当|Fs|≤μFn，节点i，j无相对运动，Fs=μknus；当|Fs|>μFn，节点i、j发生相对运动，摩擦力大小为Fs=μFnus。其中，Fn为接触单元法向相互作用力。

如图2(b)所示，从t时刻到t+1时刻，节点i、j的切向位移矢量us可由式(3)、(4)、(5)计算得出。

u=v′-v0

(3)

un=uv′2/|v′|2

(4)

us=u-un

(5)

2 建模方法

2.1 织物拓扑结构的建立

本文建立的三维正交织物模型由低结晶碳化硅纤维组成，纱线截面积为8.66×10-8m2，纤维轴向弹性模量为190 GPa，纤维横向弹性模量约为轴向的1/10，纤维密度为2 500 kg/m3。三维正交织物组织结构如图3所示，可以看出虚线框内为1个代表性体积单元。该单元内2根结构对称的接结经纱捆绑1列纬纱，浮长为1个组织点。由真实织物样本测得该结构代表性体积单元长度、宽度及厚度，分别为0.002 903、0.001 587 5和0.003 82 m。织物拓扑结构建立步骤：1)将经纱、纬纱和接结经纱分别定义为3种不同的纱线类型。纬向包含纬纱，经向包含经纱、接结经纱。2)依次将纬纱、经纱和接结纱结构转换为矩阵表征。

图3 三维正交织物组织结构Fig.3 Three-dimensional orthogonal fabric structure

由图3可以看出：经纱共有9列，由上至下分别对应编号1#～9#；纬纱共有10行，由上至下依次对应编号11#～20#；经纬纱线交替排列，经纱列数比纬纱行数少1。经纱的位置矩阵由与纬纱的相对位置决定。令位于19#和20#纬纱之间的9#经纱位置矩阵为(1,1)，位于18#和19#纬纱之间的8#经纱位置矩阵为(2,2)，以此类推。

接结经纱的位置矩阵定义方式与经纱类似。0#和10#接结经纱的捆绑方向(连接纬纱方向)呈对称分布，其位置矩阵由与纬纱的相对位置决定。例如，0#接结经纱位于第1列纬纱之下和第2列纬纱之上，其位置矩阵为(10,0)。同理，10#接结经纱位于第1列纬纱之上和第2列纬纱之下，其位置矩阵为(0,10)。受周期性边界条件的约束，接结经纱的首尾高度应保持一致，由内置算法自动生成。

通过以上方法得到三维正交织物拓扑结构，如图4所示。

图4 三维正交织物拓扑结构Fig.4 Three-dimensional orthogonal woven topology

2.2 织物建模过程

数字单元法建模流程如图5所示。数字单元法建模过程对应以下5个步骤：1)输入材料参数。2)将织物组织结构转换为矩阵表征，在系统中建立织物拓扑结构。3)设置迭代参数，在时域中利用多次迭代分析模拟整个织造过程。4)虚线框内为整个迭代分析过程。该过程以数字杆单元和节点为基数循环。首先判断和创建纤维间的接触单元对，并计算其相互作用力大小；其次通过纱线纤维化离散和纤维离散，提高模型精度和获得纱线真实截面形状。5)最后判断模型是否稳定，即达到最小势能，如果未稳定则返回步骤4)继续分析，稳定则输出最终模型。

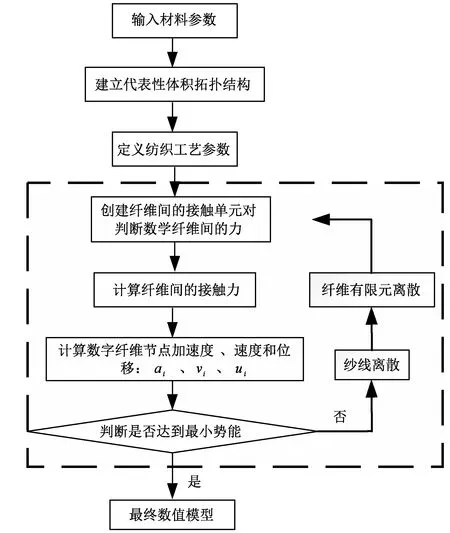
图5 数字单元法建模流程Fig.5 Flow chart of digital element approach modeling

3 织造过程模拟与结果分析

根据文献[13-14]，选取本次仿真所用纬纱、经纱和接结经纱张力值分别为0.2、0.2、0.01 N，分别建立了精度递进的5种单胞模型。不同仿真时间的三维正交织物织造过程模拟如图6所示。每种模型的纱线分别由4、7、12、19、37根数字纤维组成，其织造过程大致分为3个阶段。模型1如图6(a)所示，由2次离散得到4根数字纤维模型：第1次离散是在初次运算后将纱线纤维化离散为2根数字纤维；第2次离散是在将每根数字纤维再离散为2根数字纤维。模型2如图6(b)所示，由1次离散得到7根数字纤维模型。模型3如图6(c)所示，由2次离散得到12根数字纤维模型，第1次将纱线分成4根数字纤维，第2次将每根数字纤维离散为3根数字纤维。模型4、5分别如图6(d)、(e)所示，均由1次离散得到19、37根数字纤维模型。其中，图6(b)、(d)和(e)所示的织物单胞模型，经纱线纤维化离散后其纱线截面形状从初始的圆形变为不规则的近似真实的形状。

图6 不同仿真时间的三维正交织物织造过程模拟Fig.6 Simulation of three-dimensional orthogonal woven fabric weaving process with different simulation time. (a) Model 1; (b) Model 2; (c) Model 3; (d) Model 4; (e) Model 5

3.1 纤维间摩擦对节点力和势能影响

织物单胞势能U由纤维间的张力势能Ut和接触势能Uc组成，其中接触势能由2个接触单元内的节点作用力和摩擦力构成，可由式(6)计算得出。

(6)

式中：Uci为接触势能，J;i为接触单元对的编号；2个相互接触的节点编号分别为i1和i2，其接触势能Uci1和Uci2可由式(7)、(8)计算得出。

(7)

(8)

式中，rip为Uci1和Uci2之比，可由式(9)计算得出。

(9)

式中：Ei1为节点i1所在纤维的轴向弹性模量，Pa；Ei2为节点i1和i2所在纤维的轴向弹性模量，Pa；Li1为节点i1所在纤维的杆单元长度，m；Li2为节点i2所在纤维的杆单元长度，m。

接触势能Uci可由式(10)计算得出。

Uci=0.5Fi(Ri-lci)

(10)

式中：Ri为节点i1所在的纤维半径和节点i2所在的纤维半径之和,m；lci为节点间距，m；Fi为接触力,N。Fi可由式(11)计算得出。

(11)

节点平均作用力和时间关系见图7。可以看出：37根和7根数字纤维的节点平均作用力在计算初期，出现较大波动；20 ms以后，只有12根数字纤维模型在60 ms附近出现小幅波动，其余4个模型的节点平均作用力均逐渐平衡，并在仿真结束时趋近于0。

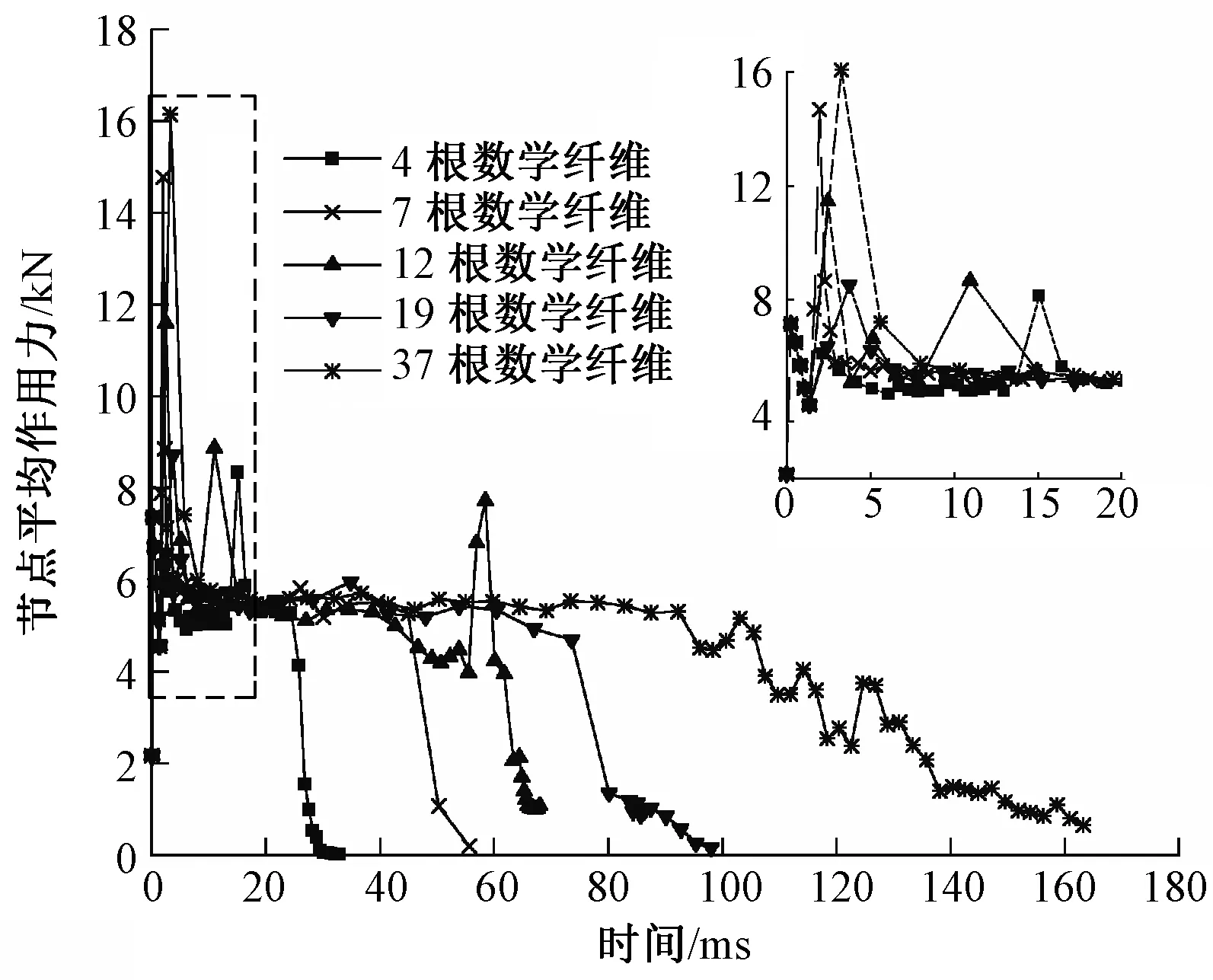
图7 节点平均作用力和时间关系Fig.7 Relationship between average nodal force and time

织物单胞势能和时间关系见图8。可以看出，5个模型的单胞势能在仿真过程中均呈现下降趋势。当节点平均作用力降低，势能也随之降低；当势能趋于平衡时，节点平均作用力趋近于0，此时单胞中仅剩张力势能。因此，纱线纤维化离散程度越高，纤维间的张力势能越小。

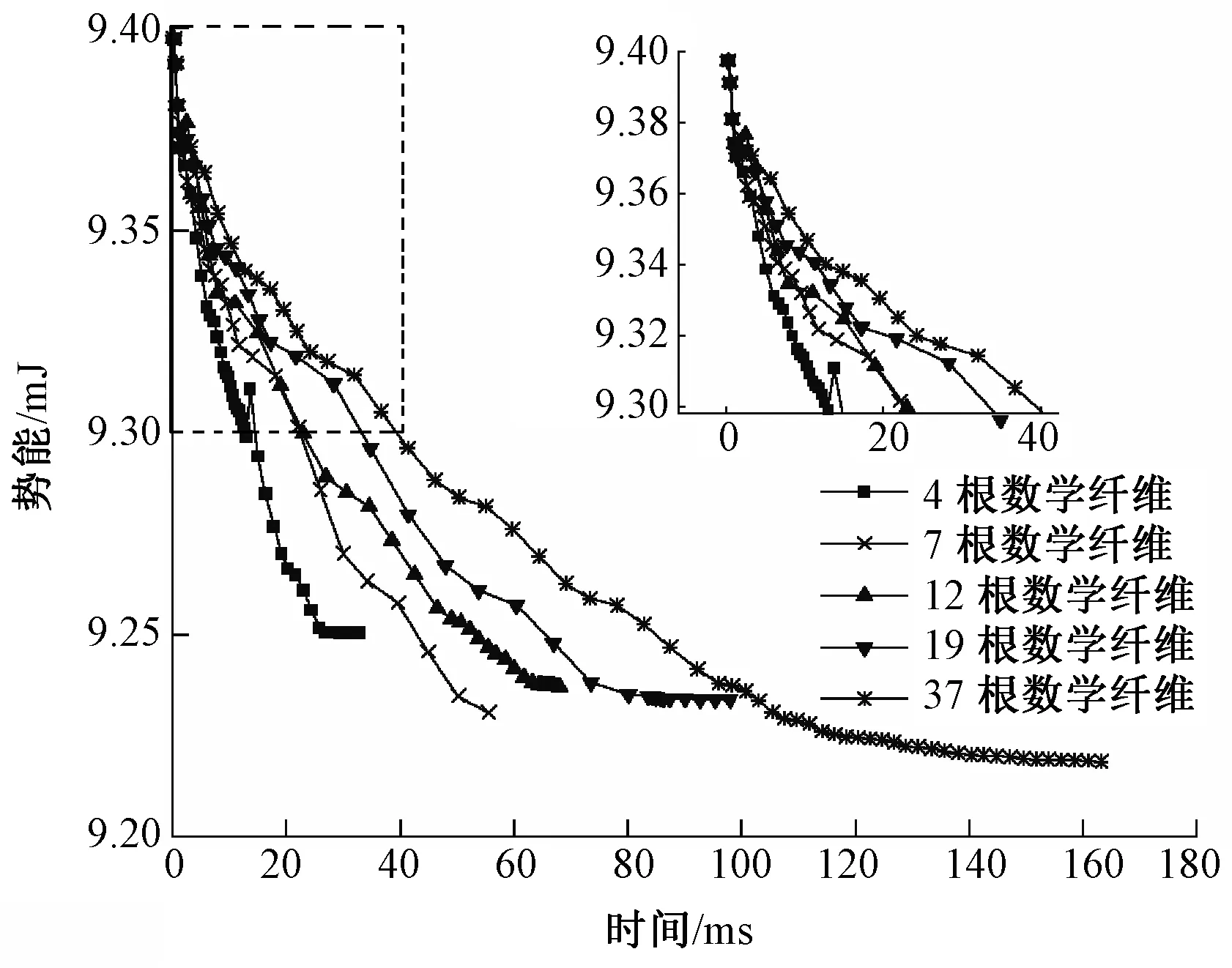
图8 织物单胞势能和时间关系Fig.8 Relationship between unit-cell potential energy and time

图9 织物单胞模型与切片显微图像的正视图对比结果Fig.9 Front view comparison results between fabric unit-cell model and microscope picture. (a) Model 1; (b) Model 2; (c) Model 3; (d) Model 4; (e) Model 5

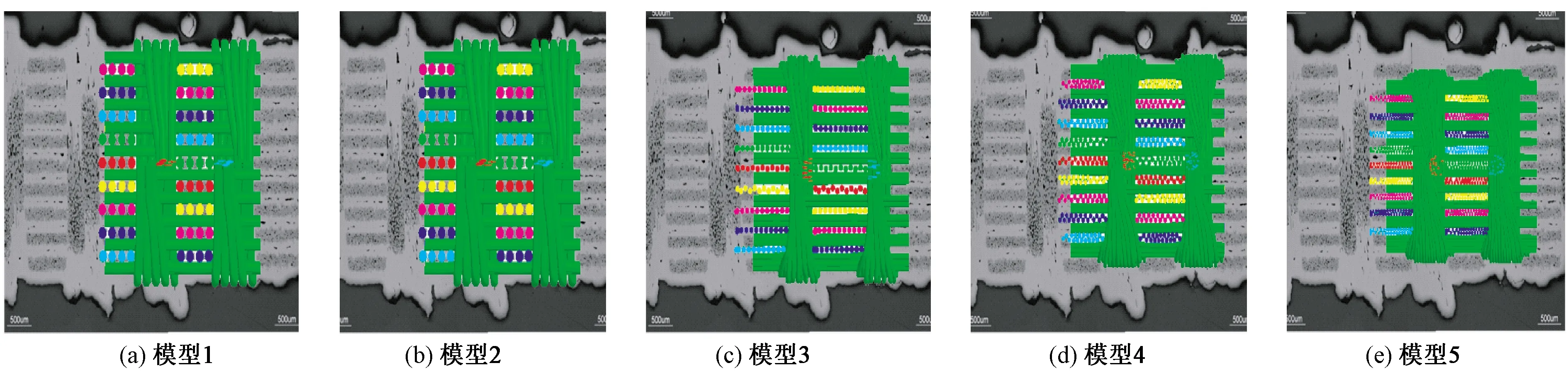
图10 织物单胞模型与切片显微图像的侧视图对比结果Fig.10 Side view comparison results between fabric unit-cell model and microscope picture. (a) Model 1; (b) Model 2; (c) Model 3; (d) Model 4; (e) Model 5

3.2 纱线纤维化离散程度对几何结构影响

三维正交织物织造过程数据如表1所示。每个织物模型的织造过程分为3个阶段，每个阶段用迭代次数划分。每次迭代后获得的仿真结果与图6三维正交织物织造过程模拟中展示的单胞微观几何结构一一对应。每个阶段的纱线纤维化离散程度、纤维体积分数以及累计耗时可由表1示出。

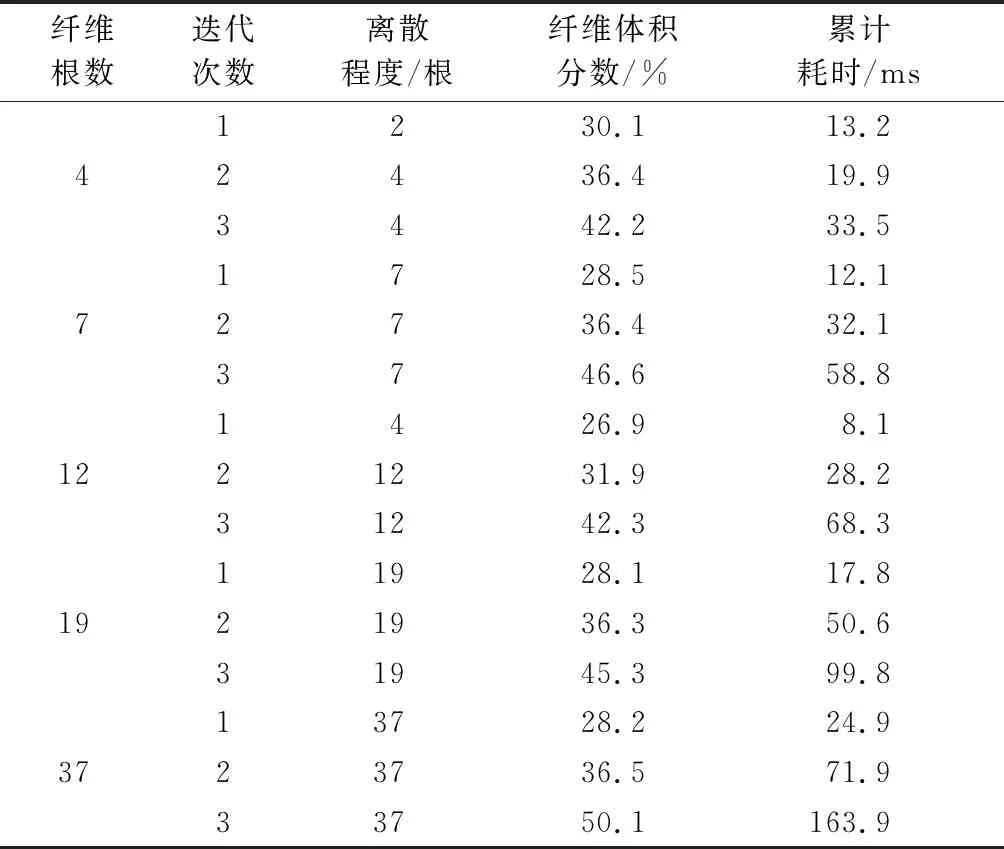
表1 三维正交织物织造过程数据Tab.1 Simulation parameters of three-dimensional orthogonal woven fabric weaving process

织物单胞模型与切片显微图像的正视图对比结果见图9，织物单胞模型与切片显微图像的侧视图对比结果见图10。

每根纱线由19根数字纤维组成的织物模型与显微图片拟合度最高，且随着纱线纤维化离散程度提高，模型几何结构更均匀，纱线空间构型更精确。5个模型厚度略低于真实织物厚度，这是因为在数值模拟中，模型的势能达到最小时方可结束计算，而三维机织过程是个动态的过程，织物的微观几何形状受织造速度和纱线张力等因素的影响，较难达到最小势能状态。

织物模型厚度随时间的变化如图11所示。可以看出，纱线所含数字纤维数量越多，结构稳定时织物的厚度越小，织物厚度下降速度越慢，达到稳定所需时间越长。其中37根数字纤维模型计算耗时约为其余模型的2～5倍。

图11 织物模型厚度随时间的变化Fig.11 Change of fabric thickness with time

通过对比织物模型与实验所得织物样本的6个因素(微观几何结构、节点平均作用力、势能、仿真耗时、织物厚度、纤维体积分数)可以看出：37根、12根和7根数字纤维模型的节点平均作用力在仿真的不同时期出现波动；纱线纤维化离散程度越高，织物结构稳定时的势能越小、厚度越小、纤维体积分数越大，纱线空间构型越接近真实纱线形态。综合所建模型稳定性、仿真耗时和与切片显微图像的重合度得出，对于三维正交织物而言，将每根纱线离散为19根数字纤维的建模方法为较优。