新型外转子升船机的研究与探索
2021-01-05李昕涛韩增强
李昕涛,韩增强
(1.太原科技大学 重型机械教育部工程研究中心,山西 太原 030024 ;2.太原科技大学 电子信息工程工程学院,山西 太原 030024)
0 前言
在内河通航中,传统的多级船闸[1]通航,存在着下泄内河大坝的蓄水水量,直接造成大坝发电量的减少,综合效益的下降;而垂直升船机具有在不影响大坝蓄水量的同时,可以有效实现内河船舶的通航[2,3]。目前,国内外在航运领域,将船舶提升一定高度所采用的装置有多种,如电动卷扬机提升、齿轮齿条传动提升、水利驱动提升等[4,5];现有垂直升船机结构复杂、运营成本高,由于提升承船厢载荷大,往往需要多台大型电机同步驱动,加之确保船舶稳定提升,造成了控制难度高,往往带来通航能力取决于垂直升船机的安全运行能力[6,7]。据此,本文提出了外转子电机拖动的升船机[8]。
1 外转子升船机的结构
新型外转子升船机结构如图1所示,在坝体之间的水面上放置有承船厢,承船厢通过皮带,并经过第一导向轮与外转子电机的两侧转筒连接。坝体的外侧分别设有配重,配重通过皮带,并经过第二导向轮与外转子电机两侧转筒连接;外转子电机及其提升机构结构相同,对称布置安装在坝体上。

图1 升船机结构示意图
升船机单侧外转子电机传动布置,如图1c所示,外转子电机的中心轴通过支架固定安装在坝体上,在其皮带转筒通过螺栓与皮带连接,在皮带转筒的中间位置安装有前后制动器。
此时,配重抵偿升船厢自重,外转子永磁同步电机仅提供运行的驱动力,减少运营成本。在轴承载荷平衡的情况下,外转子电动机驱动仅需克服轴承的摩擦力,实现升船机匀速起降运行。
2 垂直升船机力学分析
2.1 外转子电机驱动的力学分析
如图1所示,设承船厢的驱动力为F驱动,根据静力学力学定律(以向上为力的正方向)可知:
F驱动+G配重-G承船厢=M承船厢a承船厢
在确保水位不变的条件下,承船厢内的船舶数量与大小,都不影响升船水厢的重量G承船厢;因此,当外转子电机驱动的垂直升船机结构确保了承船厢与配重等重时,其外转子电机的驱动力F驱动仅提供了升船机升降时所需承船厢升降加速度a承船厢的力,即当G配重=G承船厢时,F驱动=M承船厢a承船厢。此时,设承船厢对通航船舶的浮力F船浮力,根据阿基米德原理和牛顿力学定律知,承船厢中船舶的受力F船舶为
化简可得
可知,船舶的提升(下降)加速度取决于排开水体积V船排的变化,设排开水体积V船排的变化为ΔV船排,则有
V船排+ΔV船排=a承船厢b承船厢(h液面+Δh液面)
式中,a承船厢为承船厢的长度;b承船厢为承船厢的宽度。
由此可知,船舶排开水体积V船排的变化,提供了船舶的加速度a船舶,由于承船厢水量一定,船舶排开水体积V船排变化ΔV船排,引起承船厢中液面高度h液面发生相应的变化Δh液面,承船厢水位的升高或下降提供了船舶上升或下降的动力。
设升船机承船厢中运送n艘船只,暂不考虑船只间的耦合振动对承船厢液面的影响下,则n艘船只对承船厢液面变化的影响为
将其列写微分方程为

每艘船的排开水的体积和其吃水线有关,当升船机向上提升时,每艘船相对于水面向下运动深度是不同的,船舶侧立面对水的压力也不一样,因此,产生水面的波动,带来承船厢的摆动[9-11]。
此时,若承船厢中通航船舶型号一致时,根据水弹性动态响应,易引发水体的共振,带来控制难度增加。外转子电动机驱动可以实现匀速运行,仅在其加、减速过程出现共振问题,通过智能算法的平滑性控制和制动器的投入,可以有效地减少承船厢水体的晃动。
2.2 承船厢运行偏载受力的分析
由于承船厢上下运行时,由于多吊点运行,传统的起升机构会带来侧倾,以三峡升船机为例,三峡承船厢长×宽×高(100m×20m×18m);若两侧高差相差1 cm,计算其两侧重量差为
G偏载=ρ液V偏载g=20 t
显而易见,承船厢两侧高差1 cm,偏载20 t。当承船厢向上起升时,承船厢中各船只对承船厢水位影响不同,会带来动态偏载问题。根据垂直升船机外转子电机驱动与承船厢运行偏载受力的理论分析,必须提供一种特定的智能控制算法,才能主动防御外转子电动机拖动的升船机的载荷波动、偏载问题。通过外转子永磁电机的固定时间超螺旋智能控制方法,来解决超大惯性升船机的载荷冲击问题。
3 固定时间超螺旋的智能控制算法的研究
固定时间超螺旋的智能控制方法可以在不依赖于系统初值的情况下,使系统以固定的时间收敛,改善了其收敛可靠性, 并提高了其响应时间。也就是说,自由状态下,升船机配重不能恒等于承船厢重量,带来承船厢水位的晃动,引起外转子电机负载不平衡的状态;不论初始情况下电机载荷是否一致,均布在坝体上的外转子电动机,都能在固定时间内准确到达承船厢预期的固定位置。每台电机都按照这一要求智能运行,各自采用这样的算法到达控制目标位置。在上百台外转子电动机实际运行中,一旦出现电机随机损坏后,剩余多台电机载荷突然变化,升船机依然可以正常运行。即升船机实现智能故障容错,这对于内河通航意义重大。
3.1 外转子永磁电动机数学模型的建立
升船机采用表贴式外转子永磁同步电动机,对于表贴式外转子永磁同步电动机,考虑到id对电机调速影响很小,可令id=0,建立d-q坐标系下的外转子永磁同步电动机数学模型[12,13]。
式中,ud、id、Ld、Lq、uq是坐标系变换后定子电压、电流和电感在直轴(d轴)和交轴(q轴)上的分量值,且满足Ld=Lq=Ls;R为定子电阻;pn为电机磁极对数;ψf为永磁体与定子交链的磁链;Te和TL则分别为电磁转矩、负载转矩;J为转动惯量;ω为转子机械角速度;B为摩擦系数。
外转子永磁同步电动机的调速系统的控制器以级联的形式分别构成速度外环和电流内环。其结构图如图 2 所示。

图2 外转子永磁电动机控制系统框图
3.2 外转子永磁电动机数学模型的建立
3.2.1 固定时间收敛控制律
考虑微分方程的系统:
(1)
式中,x=[x1,x2,…,xN]T∈RN,F(x):D∈RN在原点的开区间D∈RN上是连续的,且F(0)=0。
若任意给定初始时间t0和初始状态x0∈D,都存在时刻T(x0),使系统(1)的每一个解x(t)满足关系
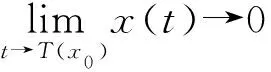
(2)
则系统(1)的平衡点x=0是有限时间稳定的,如果原点是在N=RN有限时间稳定,则其是“全局有限时间稳定”平衡。此外,原点的有限时间稳定性意味着原点的渐近稳定性。学者 Zuo Z 提出了固定时间稳定性的概念,无论初始条件如何,都能提供收敛时间的一致有界性[14]。
定义1:原点被认为式(1)的“固定时间稳定”平衡点,如果全局有限时间稳定的并且建立时间函数T(x0)是有界的,即,存在Tmax>0,且 ∀x0∈RN,都有T(x0) 引理1:考虑一个标量系统 (3) 其中α>0,β>0,并且m、n、p、q是满足m>n且p (4) 由式(4)可知,系统的收敛时间仅依赖与系统的固有参数m、n、p、q、α和β,与系统的初始状态无关,因此可以以设定的方式保证收敛时间。 3.2.2 固定时间超螺旋收敛控制律 定义:本文所提出的式(1)被称为是在原点处收敛的固定时间。若存在一个时间T,对所有t≥T从任何初始条件x0开始,都有系统的状态x(t)=0成立。 Panathula,等学者提出并研究一个连续的控制率[15]: (5) 式中,λ1,λ2,a>0 且p>1。 从而得出系统的超螺旋控制率的表达为 (6) 考虑动态系统存在的扰动ξ(t),以常数L为边界,则状态变量x(t)和y(t)均在固定时间内均匀的收敛于原点。 (7) 由式(7)可知,公式右边代表的是超螺旋系统(式6)的收敛固定时间的上限估计,此值独立于未知的初始值,并不受初始状态x(0)的影响。这意味着对于任何初始条件x(0),公式(6)所表示的超螺旋系统的两个状态变量x(t)、y(t)在有限时间Tf不大于式(4)中的上限估计值时,均能可靠收敛到原点。 3.2.3 速度控制器设计 对固定时间以及超螺旋控制率的数学模型分析,设计外转子永磁同步电动机的控制器。 定义外转子永磁同步电动机的状态变量: x1=ωref-ω (8) 式中,x1为控制系统的角速度误差;ωref为给定的机械角速度;ω为实际角速度。 考虑到摩擦系数B很小,忽略摩擦系数,由公式(1)可得, (9) 定义iq为u,则式(9)变为 (10) 基于固定时间理论表达式(3)和超螺旋表达式(6),故而,可将控制器设计为 (11) 将式(11)代入式(10)中可将其变形为 (12) 式(12)为所设计的超螺旋固定时间控制方程。由固定时间定理的公式(4)可知,系统的收敛时间T与系统的初始变量参数无关。 为验证设计控制器(12)的稳定性,定义 Lyapunov 函数为 (13) 同时,由建立的时间 可知,系统的收敛时间不大于(4)中的上限估计值,故均会可靠收敛到原点。 在Matlab/Simulink中搭建外转子永磁同步电机调速系统仿真模型[16-18]。用以验证该控制算法的可靠性,仿真中所用电机的参数设置为定子电阻R=2.875 Ω, 定子电感Ls=8.5 H,转动惯量J= 0.003 kg·m2,永磁体磁链f=0.175 Wb。仿真结果如图 3~7 所示。 图3 转速的仿真结果 图4 三相电流的仿真结果 图5 电磁转矩的仿真结果 图3 ~图5分别为电机转速为1 000 r/min 时的转速、三相电流以及电磁转矩的仿真结果图。可以看出,转速的动态响应快,超调量小,同时在 0.2 s 时突加负载TL=2 N·m后,快速稳定性。 设置电动机转速的初始误差分别为250 r/min、500 r/min、750 r/min、1 000 r/min,图6在0.2 s时突加负载后,四种不同初始误差的响应曲线均在约0.1 s时间内收敛到零,且抖振较小,较好的提高了系统的抗干扰能力。由图7可知,系统在不同的初始转速误差的条件下,其转速误差减小到零的时间基本一致,即其收敛时间均约为0.02 s,与初始误差无关。 图6 0.2 s突加负载时的仿真结果 图7 四种不同转速误差下的收敛时间仿真结果 外转子永磁电动机在升船机载荷不均的状态下,可实现速度快速同步;承船厢与每个外转子电机速度一致,即动态平衡运行[19-20]。 本文对外转子升船机进行了力学理论分析,并通过理论分析得出结论: (1)外转子升船机采用配重抵偿升船厢自重,电机仅提供承船厢运行的动力,大大降低了垂直升船机运行成本。 (2)自由状态下,配重与承船厢重量偏差来源于——承船厢升降过程中水位的晃动,故外转子电机载荷不均衡; (3)通过对固定时间超螺旋智能算法应用于外转子永磁电机控制的研究,其仿真结果表明智能算法有效实现动态平衡运行;为新型外转子升船机的研制提供了理论依据。
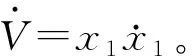
3.2 仿真结果分析





4 结论
