基于移动主成分分析特征的智能损伤诊断方法

梁杰明, 刘逸平, 陈敬松, 周立成, 刘泽佳, 汤立群

(1.华南理工大学 土木与交通学院,广东 广州 510641; 2.华南理工大学 亚热带建筑科学国家重点实验室,广东 广州 510641; 3.广州市高速公路有限公司,广东 广州 510289)

为避免因损伤导致桥梁结构失效和生命财产损失,目前多数大型桥梁安装了健康监测系统,并收集了大量监测数据以供桥梁状态评估及日常维护。桥梁监测数据除了包含桥梁损伤信息外,还受到众多因素如随机外荷载和噪声的影响,如何利用桥梁监测数据识别损伤仍是难题。

目前已有多种基于数据驱动的损伤检测方法,如小波、自回归模型等,用于实验模型的损伤检测时识别效果很好,但是在桥梁运营过程中,实际荷载状况复杂,这些方法仍难以满足实际工程需求[1-2]。

近年来,人工智能算法因其处理不确定性和非线性问题的能力优异而受到广泛重视。在结构健康监测领域,国内外研究者使用机器学习从桥梁监测数据中挖掘有价值的信息[3]。数值计算结果表明,机器学习在识别损伤方面有更高的精度[4-5]。然而,机器学习模型仍存在易受噪声干扰、性能依赖人工特征及现有特征不能满足高精度损伤识别的要求等问题[6]。

主成分分析(principal component analysis, PCA)方法能够压缩数据并提取数据特征,在结构损伤识别领域上被广泛使用。文献[7]提出以桥梁响应的移动主成分分析(moving principal component analysis, MPCA)第一特征向量为诊断桥梁损伤的指标,数值计算表明该方法比小波方法和傅里叶变换方法等有更强的损伤识别能力;文献[8]将MPCA方法与4种回归分析模型相结合,进一步提升了损伤识别效果;文献[9]将MPCA方法与机器学习模型结合来诊断桥梁损伤,损伤识别结果表明,以MPCA特征向量为输入的机器学习模型能有效提升算法的抗噪性,且能克服MPCA方法无法识别微小损伤的缺点。然而,以MPCA特征向量为输入的机器学习模型难以识别早期损伤。

本文提出一种基于MPCA的优化特征——特征向量差方向角(directional angle of eigenvector variation, DAEV),将DAEV与机器学习模型结合,以加载实测温度荷载的双跨连续梁为研究对象,将通过数值仿真所得应变数据的DAEV特征作为机器学习模型的输入,建立智能模型识别桥梁损伤。

本文研究发现,与MPCA特征向量相比,DAEV特征对损伤更敏感,且以DAEV为输入的机器学习模型损伤识别准确率更高,对早期损伤有更强的识别能力。

1 基于MPCA的特征工程

1.1 MPCA特征向量

MPCA是提取时间序列数据的常用方法。它在PCA的基础上引入向前移动的固定大小的时间窗,并运用PCA原理获得特征向量的时间序列。

以大小为T、滑动步长为L的时间窗对Q维数据作MPCA分析,第k次对时间窗内数据矩阵X(k)作PCA处理时有:

X(k)=

(1)

对X(k)作正则化处理后,计算其协方差矩阵C的特征值与特征向量。通常以最大特征值和对应的第一特征向量作为数据特征。随着k值增大,能得到特征向量或特征值的时程曲线。当桥梁损伤发生,桥梁响应发生变化,特征向量相应地改变,由此以特征向量作为输入的机器学习能识别损伤。

然而,以MPCA特征向量为输入的机器学习模型在识别早期损伤方面仍有不足。PCA、MPCA基本原理都是将原始数据映射到另一数据空间中,特征向量则为新空间的坐标基,特征向量的分量则为新的坐标基在原始坐标上的投影。由(1)式可知,桥梁损伤发生后,随时间窗滑动,时间窗内健康桥梁的响应数据逐渐减少,损伤桥梁响应数据增多,MPCA处理得到的特征向量逐渐变化。在损伤发生后的初期,此时的MPCA特征向量与健康桥梁响应的特征向量相比,相对变化较小,不利于及时识别损伤,机器学习模型难以根据该部分特征识别桥梁损伤。在特征向量变化过程中,若桥梁损伤程度没有大幅度变化,则特征向量变化方向稳定,因此根据特征向量的变化方向能够诊断桥梁损伤并实现损伤早期识别。

1.2 MPCA特征向量差方位角

DAEV表征MPCA特征向量变化的方向[10]。假设桥梁初始状态为无损伤状态,持续一段时间后桥梁状态变为未知,由此将监测数据分割为2部分:① 初始状态下的无损伤桥梁的监测数据;② 未知状态(观测状态)下的桥梁监测数据。首先,计算观测状态与无损伤状态下第一主特征向量相对变化量ΔΨ1(k):

(2)

(3)

其中,Δψ1j(k)为矢量ΔΨ1(k)的分量。

DAEVθ1(k)的分量θ1j(k)为:

(4)

(5)

2 仿真桥梁损伤识别实验

通过数值仿真生成模拟损伤工况下桥梁响应监测数据,对比数据的MPCA特征向量和DAEV特征对损伤的灵敏性。

2.1 仿真桥梁模型

实验用模型为素混凝土双跨梁模型,如图1所示,桥梁长10.0 m、高0.5 m、厚0.3 m,桥梁被滑动铰支座分为2跨,1跨为5.0 m,桥梁的一端支座为固定铰支座,另一端为滑动铰支座。桥梁材料为C50混凝土,弹性模量为34.5 GPa,泊松比为0.2,热膨胀系数为10-5/℃。梁长均分为200份,梁高均分为10份,梁模型按200×10平均划分网格。

图1 桥梁模型示意图

桥梁上随时间变化的温度荷载如图2所示。

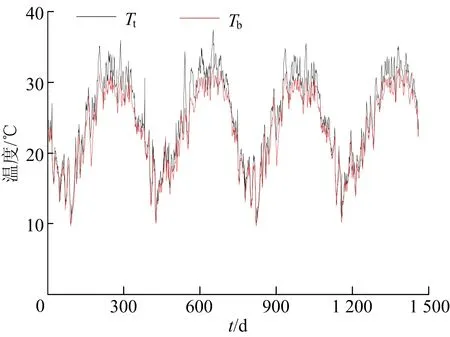
图2 顶底板温度温度荷载

图2中,Tt、Tb分别为桥梁顶板和底板处的温度。在桥梁的顶板和底板施加实际测量的4 a的温度荷载,桥梁顶、底板之间的温度分布为沿桥高呈指数分布的温度。

桥梁内温度梯度计算公式为:

Ty=Tb+ΔT(y)

(6)

(7)

其中,Ty为高度y处混凝土梁温度;T0为桥梁顶、底板的温差[11]。温度荷载呈现以1 a为周期的周期性变化趋势。

2.2 损伤工况和数据集

桥梁损伤模拟桥梁开裂,损伤从桥梁底部单元发生,沿梁高发展,如图1所示。设定损伤所在网格材料模量折减,且假设损伤发生后损伤不会加剧。损伤有长度、位置及模量折减程度3类属性。损伤的长度有梁高的10%、20%、30%、40%、50%,共5种情况;损伤的位置有200种,分别对应桥梁模型每列网格;损伤的模量折减程度有13种,分别是模量的1%、2%、3%、4%、5%、6%、7%、8%、9%、10%、20%、30%、40%。3类属性组合共13 000种工况,设定损伤于第3年年初发生。损伤工况命名以损伤长度、损伤位置、损伤程度组成的向量表示,即S=[Length(%) Position Level(%)],其中无损伤工况为S=[0 0 0]。桥梁响应样本为桥梁上安装的20个传感器在同一时间监测得到的响应数据组成的向量。对响应数据按1 a的数据长度为窗口大小提取MPCA特征向量和DAEV特征。

2.3 特征向量与DAEV特征对比

为比较不同数据特征优劣,考察MPCA特征向量Ψ1与DAEVθ1j随时间的变化规律。S=[50 5 20]与S=[0 0 0]的响应特征向量Ψ1分量ψ11和DAEV分量θ11对比如图3所示。图3中,横坐标以损伤发生时刻(第3年第1天)为0时刻,负数表示损伤发生前,正数表示损伤发生后。

由图3a可知,无损伤桥梁数据的特征向量一直保持稳定,而有损伤桥梁数据的特征向量在损伤发生前保持稳定,损伤发生后的第1年里特征向量逐渐变化,直到第2年才达到另一个稳定状态。这是由于MPCA的时间窗长度为1 a,损伤发生后的第1年间,时间窗内无损伤状态下的数据逐渐减少,有损伤状态下的数据逐渐增多,从而造成特征向量的缓慢偏移,直至时间窗内均为有损伤状态下的数据后达到稳定状态。从图3a也可以看出,损伤发生的前3月内,桥梁响应的MPCA特征向量与无损伤状态下的特征向量非常接近,前6月特征向量的相对变化量仅达到10月后稳定状态下相对变化量的18%。

由图3b可知,无损伤桥梁数据的DAEV特征一直保持稳定,而有损伤桥梁数据的DAEV特征在损伤发生前保持稳定,在损伤发生后即发生大幅度变化且快速达到另一个稳定状态。这种快速变化是由于DAEV特征表示待识别状态的桥梁数据的特征向量相对于无损伤状态下特征向量的方向角变化方向,在损伤刚发生时,特征向量即开始旋转,DAEV则可以在第一时间捕捉到特征向量的方向角变化方向,因此DAEV在损伤发生后呈现快速稳定的特点。

由图3a与图3b对比可知,虽然响应数据的MPCA特征向量与DAEV在稳定后均能体现桥梁状态的变化,但是DAEV对损伤比特征向量更灵敏、更利于机器学习模型识别桥梁早期损伤。

图3 损伤工况与无损伤工况响应特征对比

3 基于DAEV的智能损伤识别结果

将数据按4∶1随机划分为训练集和测试集,训练集训练机器学习模型,测试集用于测试模型的损伤识别能力。

为表征训练得到的机器学习模型识别损伤的能力,以准确率A作为评价指标,其定义为测试集中模型识别损伤标签正确的样本数量Nacc占测试集总样本数量Nall的比例,即

(8)

人工神经网络(artificial neural network, ANN)、k-近邻(k-nearest neighbor,kNN)和决策树(decision tree, DT)模型是人工智能模型中常用的几种机器学习模型。下面以桥梁响应的DAEV特征分别训练ANN、kNN及DT模型,评估模型识别损伤位置、损伤程度以及损伤长度的能力,并且与MPCA特征向量训练的模型比较,最后评估DAEV训练的模型抗噪声干扰能力。

3.1 损伤定位识别结果

测试集中ANN、kNN、DT模型分别识别桥梁损伤位置的准确率,见表1所列。

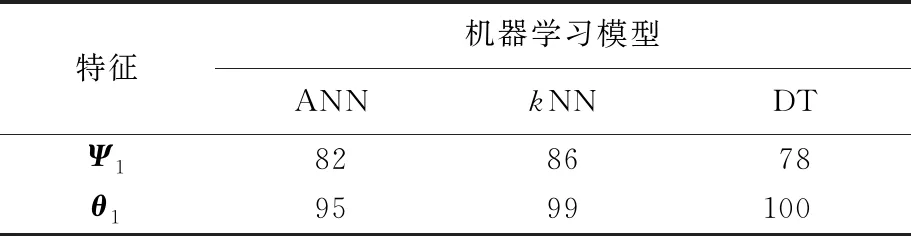
表1 测试集3种机器学习模型损伤定位的准确率 %

由表1可知,以DAEV为输入的模型损伤定位准确率比以MPCA特征向量为输入的同种模型高13%～22%。

为探索DAEV特征与MPCA特征向量训练的模型损伤定位能力差异的原因,并且验证DAEV特征训练的模型识别早期损伤能力,以月为单位统计模型识别测试集内各时间段样本中损伤位置的准确率。损伤发生后,不同时间段内样本识别准确率如图4所示。

由图4可知,以特征向量作为输入的各模型识别损伤位置准确率随时间推移逐渐上升,但是前期准确率低至20%,而以DAEV作为输入训练的机器学习模型损伤定位准确率则保持稳定,从损伤发生的第1月起均高于90%,各时间段损伤定位准确率均不低于以特征向量为输入的模型。损伤发生的前3月内,与以特征向量作为输入相比,以DAEV为输入的同类模型损伤定位准确率高52%～74%。

由2.3节可知,损伤发生后1 a内,特征向量逐渐变化,且损伤发生的前3月内,特征向量相对变化量较小,因此以特征向量为输入的模型早期损伤定位的能力较弱。而DAEV特征在损伤发生后即发生大幅度变化且保持稳定,因此以DAEV特征为输入的模型对早期损伤定位能力较强。综上所述,与特征向量相比,以DAEV为输入的机器学习模型能更好地识别早期损伤。

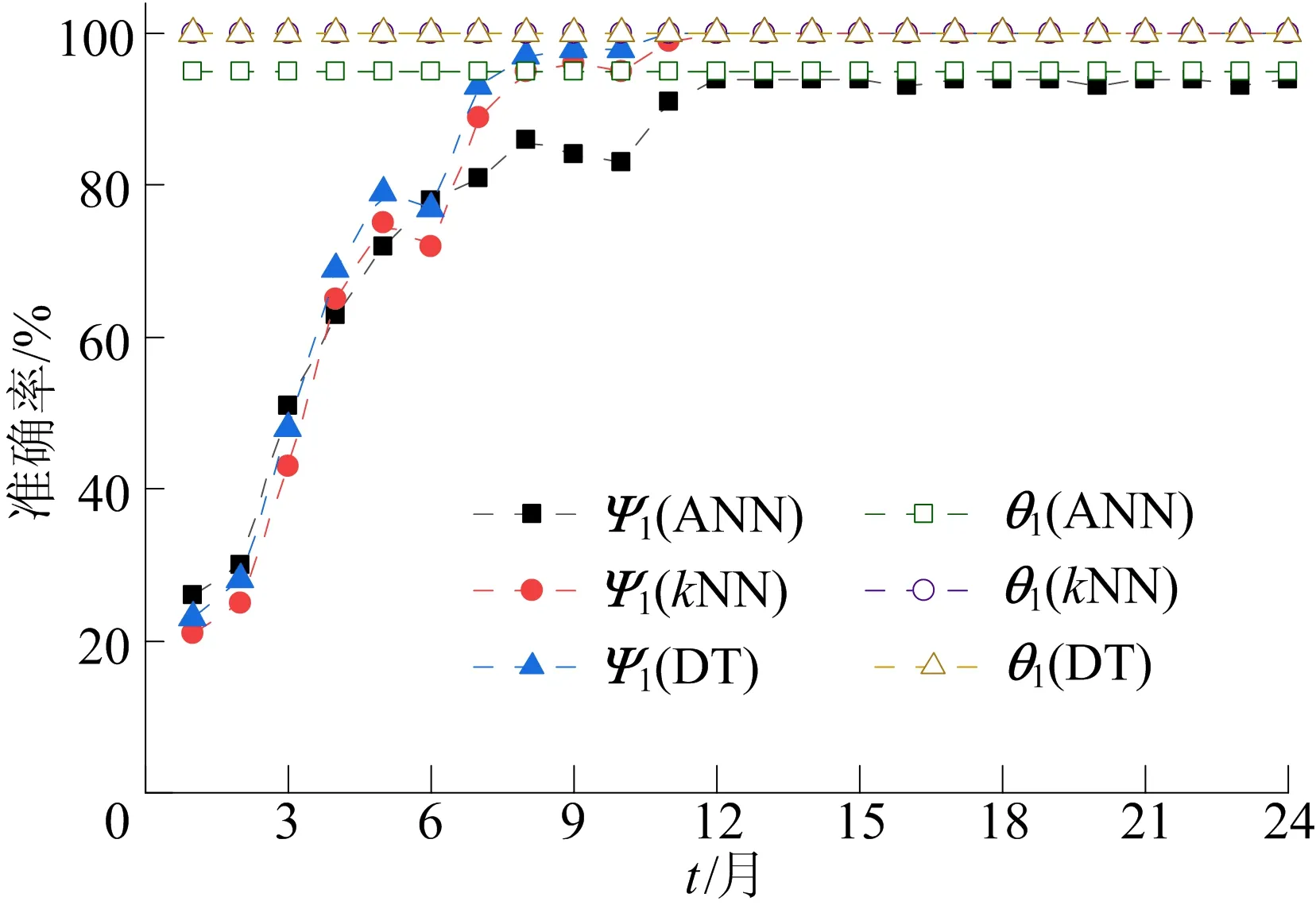
图4 不同时间段样本损伤位置识别准确率

3.2 损伤程度识别结果

测试集中ANN、kNN、DT模型以不同特征识别桥梁损伤程度的准确率,见表2所列。由表2可知，以DAEV特征为输入时比以MPCA特征向量为输入时分别高11%、16%、15%。

表2 测试集3种机器学习模型识别损伤程度的准确率 %

损伤发生后,不同时间、不同损伤程度下样本识别准确率如图5所示。

由图5a可知,损伤发生后的初期,以特征向量为输入的机器学习模型识别损伤程度的准确率较低,导致总体识别准确率低于以DAEV为输入的同类模型;损伤发生的前3月内,与以特征向量为输入相比,以DAEV为输入的同类模型损伤识别准确率高44%～79%。

由图5b可知,以MPCA特征向量为输入的模型呈现出损伤程度越大损伤识别准确率越高的趋势,而以DAEV作为模型输入时,各损伤程度损伤识别准确率相对较稳定。当桥梁损伤的模量折减程度低于5%时,以特征向量为输入的模型损伤程度识别准确率明显比以DAEV为输入时低13%～37%。各损伤程度下,数据的DAEV特征比特征向量对损伤发生更敏感。

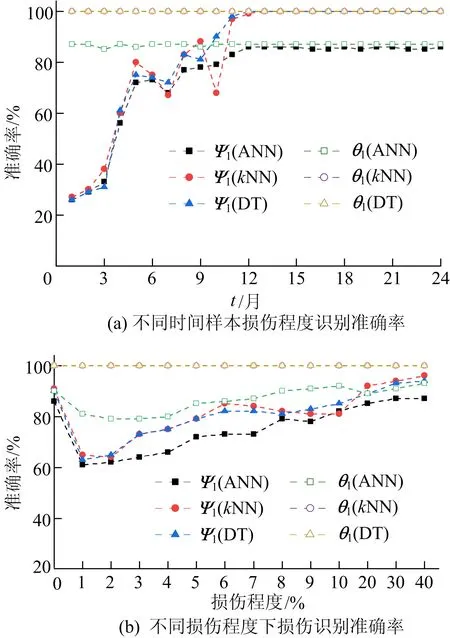
图5 3种机器学习模型识别损伤程度准确率

3.3 损伤长度识别结果

以不同特征训练的ANN、kNN、DT模型分别识别桥梁损伤长度的准确率，见表3所列。由表3可知,与MPCA特征向量相比,以DAEV特征为输入的模型识别损伤能力更强。

表3 测试集3种机器学习模型识别损伤长度的准确率 %

损伤发生后,模型识别不同时间、不同损伤长度下样本识别准确率如图6所示。

由图6a可知,损伤发生第1月内,特征向量作为输入的模型损伤长度识别准确率低至40%,随时间推移准确率逐渐上升,直至损伤发生10月后才保持稳定;而DAEV作为输入训练的机器学习模型损伤长度识别准确率一直保持稳定,从出现损伤的第1月开始均高于90%;损伤发生的前3月内,与以特征向量为输入相比,以DAEV为输入的同类模型损伤识别准确率高38%～69%。因此,以DAEV特征为模型输入能显著提高机器学习模型识别早期损伤能力。

由图6b可知,当损伤长度不小于梁高30%时,特征向量训练的模型识别损伤长度的准确率与以DAEV训练的模型相近;损伤长度小于梁高30%时,以DAEV为输入的模型比以特征向量为输入的高14%～35%。

综上所述,桥梁响应数据的DAEV特征比MPCA特征向量对损伤更敏感。

图6 3种机器学习模型识别损伤长度准确率

4 结 论

本文提出了一种优化的MPCA特征——特征向量方向角(DAEV),并将其作为机器学习模型的输入建立损伤识别算法,利用数值仿真的桥梁应变数据验证了该方法的有效性,主要结论如下:

(1) 与MPCA特征向量相比,DAEV特征在损伤发生初期即发生大幅度变化且保持稳定,能更好地表征桥梁状态的改变,对损伤更敏感。

(2) 与MPCA特征向量相比,以DAEV特征为输入的模型识别损伤能力更强,特别是在识别早期损伤方面,在损伤发生的前3月内,以DAEV特征为输入的模型比以特征向量为输入的模型的识别准确率高38%～79%。

(3) 在结构损伤发生第1月内,以DAEV特征为输入的模型损伤定位和损伤定量准确率能达到90%,能够在损伤进一步发展之前进行预警。