基于贡献因子BP神经网络的地磁适配性研究

汪金花, 张 博, 吴 兵, 郭云飞

(1.华北理工大学 矿业工程学院,河北 唐山 063210; 2.中煤航测遥感集团有限公司,陕西 西安 710199)

地磁定位具有全天时、全天候、无源、无福射等优点,近几年地磁高精度的定位技术在室内、地下工程等领域的基础研究发展迅速,成为多学科交叉研究的热点之一。地下工程地磁精确定位是依据通行路线的实测地磁序列与地磁基准数据的匹配计算来实现的,其定位精度受到区域地磁基准图、载体实时测量地磁序列、地磁匹配算法及区域适配性等因素影响。地磁适配性评价是对区域地磁空间分布特征强弱的综合分析,是地磁定位导航的基础和前提。关于地磁定位适配性研究,国内外已有一些基础研究成果。文献[1]结合地磁纹理特征提出基于地磁共生矩阵的算法用于水下地磁适配区的选择,得出水下匹配区域适配性与地磁共生矩阵反演的地磁角二阶矩、熵、对比度及相关性这些指标吻合度较高;文献[2]提出一种基于基因表达式编程的算法用于水下地磁进化合成特征的构建,得到了稳健性更好的综合适配特征;文献[3]提出基于地磁特征参数信息熵的适配区选择方法用于海域地磁适配区的选择,得出基于地磁特征参数信息熵的适配区选择方法更有效,更适合作为适配区的选择标准;文献[4]针对空域地磁场的特点利用主成分分析(principal component analysis,PCA)结合后向传播(back propagation,BP)神经网络的方法对基本地磁特征参数进行分析,得到了更好的分类精度;文献[5]提出基于BP神经网络的地形适配/误配区划分方法用于分析水域地磁场统计参量与匹配精度间的关系,得出该方法的分类精度高出传统分类方法分类结果正确率10%以上;文献[6]将改进的信息熵作为特征指标对航拍图片进行适配性分析与选择,在景象匹配制导中得到了较高的自匹配概率和较小的匹配误差;文献[7]采用矢量分析的方法构建地磁综合评价值辅助惯导系统进行水下定位导航,结果表明综合评价值可作为选择合适地磁辅助导航匹配区适宜性的定量指标;文献[8]采用免疫粒子群优化算法在水下地磁基准图中智能选择最优匹配区域,结果表明,匹配概率与匹配区域选择策略具有良好的一致性。这些适配性评价的研究大部分是构建新型的特征指标、引入BP算法或人工智能分析来改进适配性评价方法,评价精度提升明显,主要是应用于水下地磁定位区域适配性评价,关于地下工程小范围适配评价方法的研究很少。

前期大量试验结果表明,虽然地下工程空间小,巷道之间主要是线性连接方式,但是环境附加磁场的空间分布变化复杂,有些区域磁场变化大,空间分布特征明显,有些区域磁场变化平缓,空间分布差异不明显。由于不同地段地磁空间分布得不规律,需要一种有效快捷的适配性评价模型来综合评价。本文针对于地下工程地磁空间分布的特点,利用回归分析方法确定特征参数的贡献因子,改进BP神经网络的输入权值,建立了基于贡献因子BP神经网络的适配性评价模型,可为地磁辅助定位适配性评价提供参考。

1 井下磁场空间特征

地下工程实际测量的地磁场数值中包含地磁稳定场与异常场及环境磁场的综合叠加影响。实测地磁数据通常是地球基本磁场和周围环境附加磁场叠加作用的结果,即除了实际地理位置基础地磁场外,还叠加了周围铁轨、通风管道、排污管道、通信设施等产生的附加磁场,井下地磁数据具有分布特点不一致、空间分布复杂的特点。例如,有些区域地磁缓变,几十米巷道的磁异常只围绕着几百至几千nT变动;有些区域扰动较大,两点相距仅仅几米,地磁值陡增到104nT。因此,需要量化计算巷道的地磁空间分布特征具体数值,进行适配性评定。

从已有研究文献[9-12]来看,表征地磁特征的参数较多,如地磁场均值、标准差、粗糙度、粗糙方差比、地磁熵、相关系数、分形维数、累加梯度、相关距离、地磁费歇信息量、地磁编码失真量、坡度标准差等,多达十几种。根据地下工程的地磁空间分布特点,本文选取地磁标准差δ(相应的地磁空间特征因子用F1表示,下同)、峰态系数Ce(F2)、偏态系数Cf(F3)、地磁粗糙度r(F4)、粗糙方差比o(F5)、地磁信息熵G(F6)及相关系数t(F7)7个地磁空间分布特征参数,其表达式和意义见表1所列。

表1 区域磁场基本适配特征因子

这7个参数分别从地磁分布的宏观特征、微观特征以及相似特征3个层次反映地磁空间分布特征,但是对于井下小区域,每个参数贡献率不同。由表1公式可知,F2反映数值的集中程度,数值越大,数据在均值附近集中程度越高,特征性不强,不利于地磁匹配定位;F6反映区域信息量大小,数值越小,表明地磁变化越独特,有利于地磁匹配定位。分别选取F2、F62类试验数据进行特征统计,每类数据各有8个测区,F2、F6与匹配概率的相关性如图1所示。

图1 F2、F6与匹配概率的相关性

从图1可以看出,随着F2、F6增大,其地磁匹配概率逐渐降低,说明地磁空间匹配概率与F2、F6的统计特征关联性较强。每个测区地磁空间特征各异,统计的特征参数也大小不一,每个特征因子对匹配概率的影响也是不同的,因此需要在适配性评价之前,确定7个特征因子在适配性评价过程中的贡献因子大小,从而加强模型自动收敛的速度以及避免陷入局部最优。

为了研究地磁空间分布特征因子与匹配概率之间关系,可以先进行其相关性回归分析[13],确定其关联程度。7个特征因子与匹配概率的回归方程模型为:

P(F)=B0+B1F1+B2F2+…+B7F7

(1)

其中,P(F)为区域地磁匹配概率;FI(I=1,2,3,…,7)为地磁特征因子;BI(I=1,2,3,…,7)为回归系数;B0为常数。

一般情况下,回归系数大小可以间接反映该因子在适配性评价中的影响程度。当F2、F6较大时,说明该区域特征相似区段较多,地磁匹配时易出现模糊匹配,表明其适配性差;当F1、F3、F4、F7的数值较大时,说明空间分布独特性较强,适配性也较好。

2 基于BP神经网络的适配性评价

地磁适配性的评价是对井下所有巷道进行地磁空间特征的丰富度评价,可以分为定性和定量2种评价方式。定性评价是评价该区域地磁定位的适配程度,分为不适配、弱适配、适配及强适配4个等级,采用基于多属性决策判别方法,如线性距离判别、贝叶斯判别、决策树判别、BP神经网络等[14-16];定量评价是对待匹配区进行匹配概率的量化评价,从匹配实用性和准确率上进行评价,采用的算法有互相关算法、均方差算法、归一化积相关算法及平均绝对差(mean absolute devition,MAD)[17-19]算法等。

结合7个特征因子,以BP神经网络数学模型为基础,设计BP神经网络的地磁适配性评价模型为7-h-1的网络结构,如图2所示。

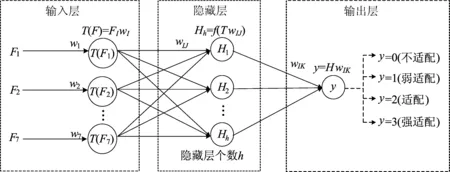
图2 地磁适配性评价的BP神经网络模型

图2中,输入层为表1中7个地磁空间分布特征因子,输入层初始权为F1～F7的贡献因子wI;隐藏层主要包含更新权值wIJ、偏置b′以及激活函数f;输出层为适配性评价等级y。从图2可以看出,BP神经网络精度和实际匹配效率受到多种因素影响,主要因素有神经元的数目、激活函数类型以及贡献因子wI。其中,神经元的数目、激活函数类型可以通过反复训练对比得出最佳结果,而贡献因子wI需要根据输入层结构和相关性来设定。

(1) 归一化处理模型。由于采集的地磁空间分布特征参数量纲不统一,需将采集的样本数据进行归一化处理。将7个输入向量归一化处理为0～1之间的数值;设x=(x1,x2,…,xm),建立一个映射f′:

(2)

其中,k=1,2,…,m;xk为需要归一化处理的样本原始数值;xmin为样本数据中最小值;xmax为样本数据中最大值。

(2) 贡献因子wI。对于(1)式,一般情况下,模型识别精度主要受到与匹配概率相关性较强的特征因子的影响较大,如F3、F4等。由于地磁适配性评价的样本较少,且在隐藏层中各个特征因子分别给予了等价权,因而可能引起网络无法收敛或陷入局部最优。为了提高模型的收敛性和达到全局最优,需要对样本特征因子的初始权进行预处理,即设定贡献因子wI。预处理过程采用最小二乘线性回归的方法进行参数估计,得出每个样本特征因子的贡献权w。预处理数学模型为:

(3)

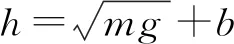
(4) 激活函数f。3种常见激活函数的对比见表2所列。通过反复试验确定最佳的激活函数。

表2 3种激活函数的对比

(5) 输出层定义。通过前向传播输出模型的计算结果,反向传播中通过设置对应的期望值y进行迭代训练。本文根据MAD算法,计算各个样本区域的磁场匹配概率,并根据不同的匹配概率划分适配性的期望值,不同期望值对应的磁场区域匹配概率见表3所列,期望值数值为适配标签。

表3 不同期望值对应的匹配概率

3 试验方案

(1) 试验数据。选取45个3 m左右的人防工程小区域,每个区域内布设3条控制线,控制线间隔为1 m,每条线上采样点间隔为1 m。使用FVM400磁通门计进行磁场数据采集,该磁通门计的参数见表4所列。

表4 FVM400磁通门计参数

每个点位采集5次数据,取其平均值作为最终的磁场数据,并根据MAD算法计算各个区域的匹配概率,剔除可能存在误差的4个区域,将余下的41个区域磁场特征因子与对应的匹配适配标签制作成训练数据集和测试数据集,分别见表5、表6所列。

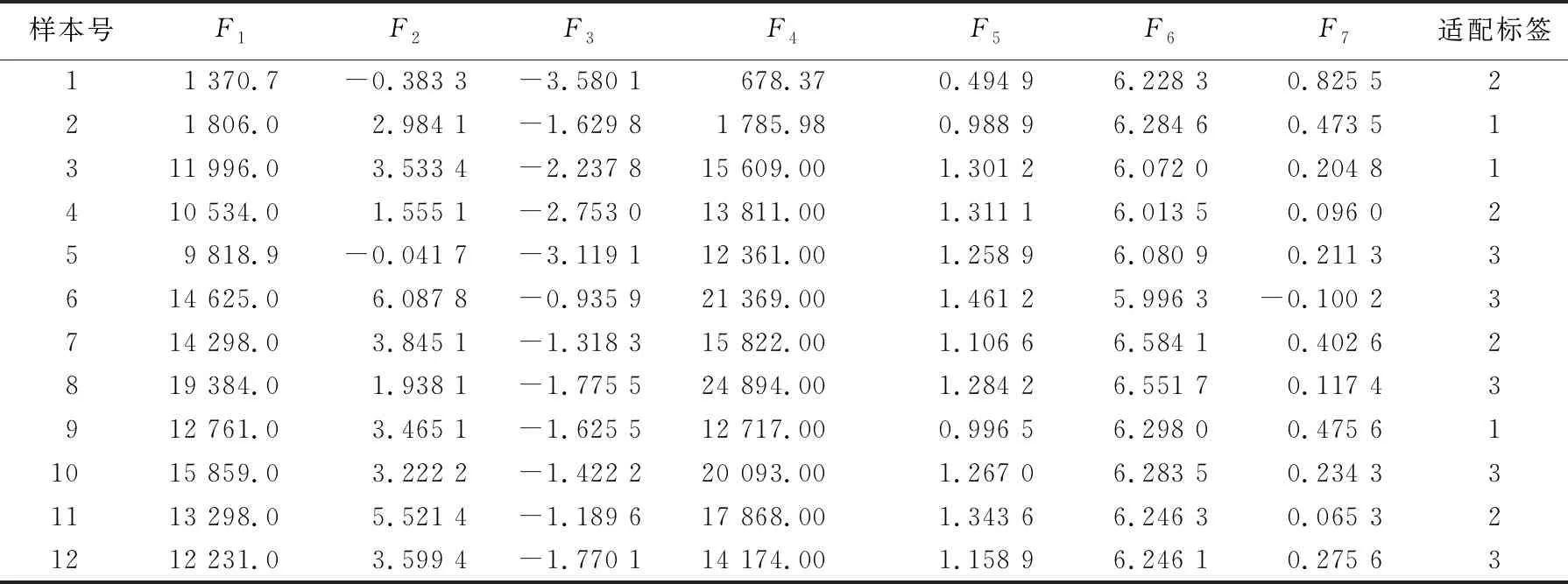
表5 磁场特征训练数据集

续表

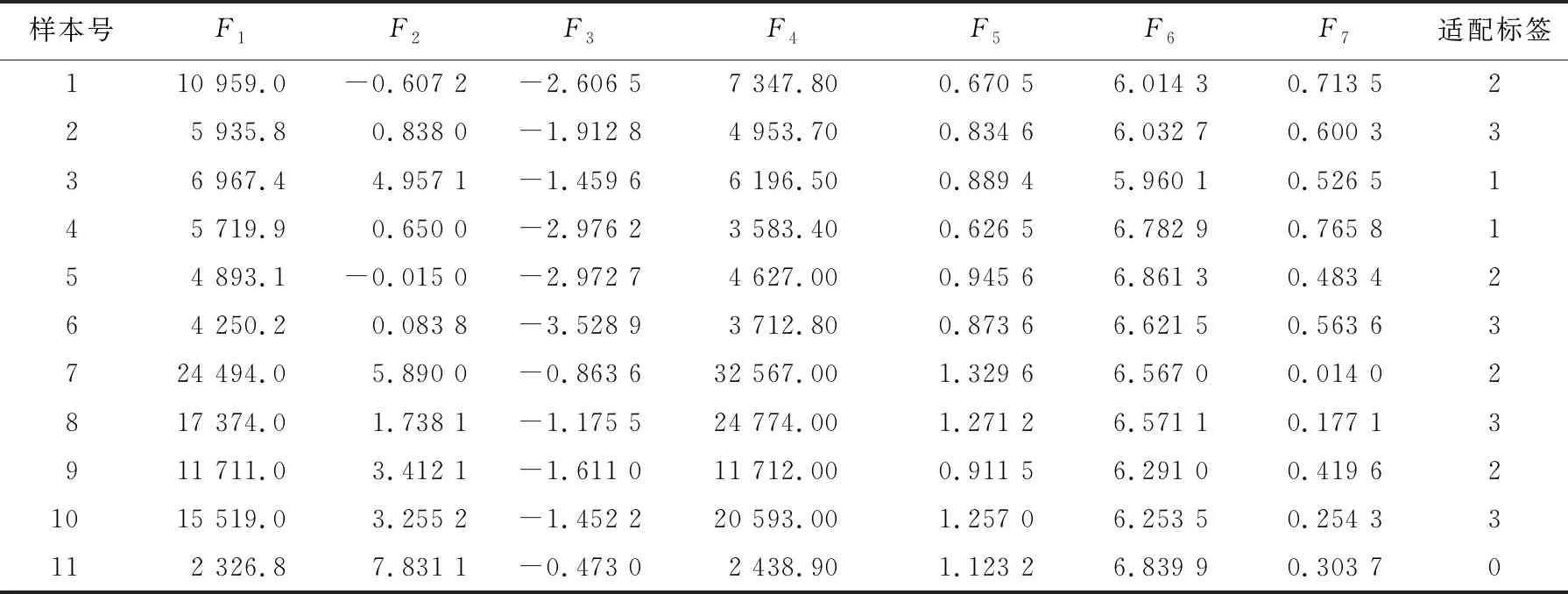
表6 磁场特征测试数据集

(2) 数据处理。在获得归一化地磁特征的7个参数后,将7个特征因子与对应的匹配概率进行基于最小二乘回归分析,根据回归结果确定7个地磁特征因子的贡献因子,将贡献因子设置为BP神经网络的初始权进行网络训练。数据处理的流程如图3所示。

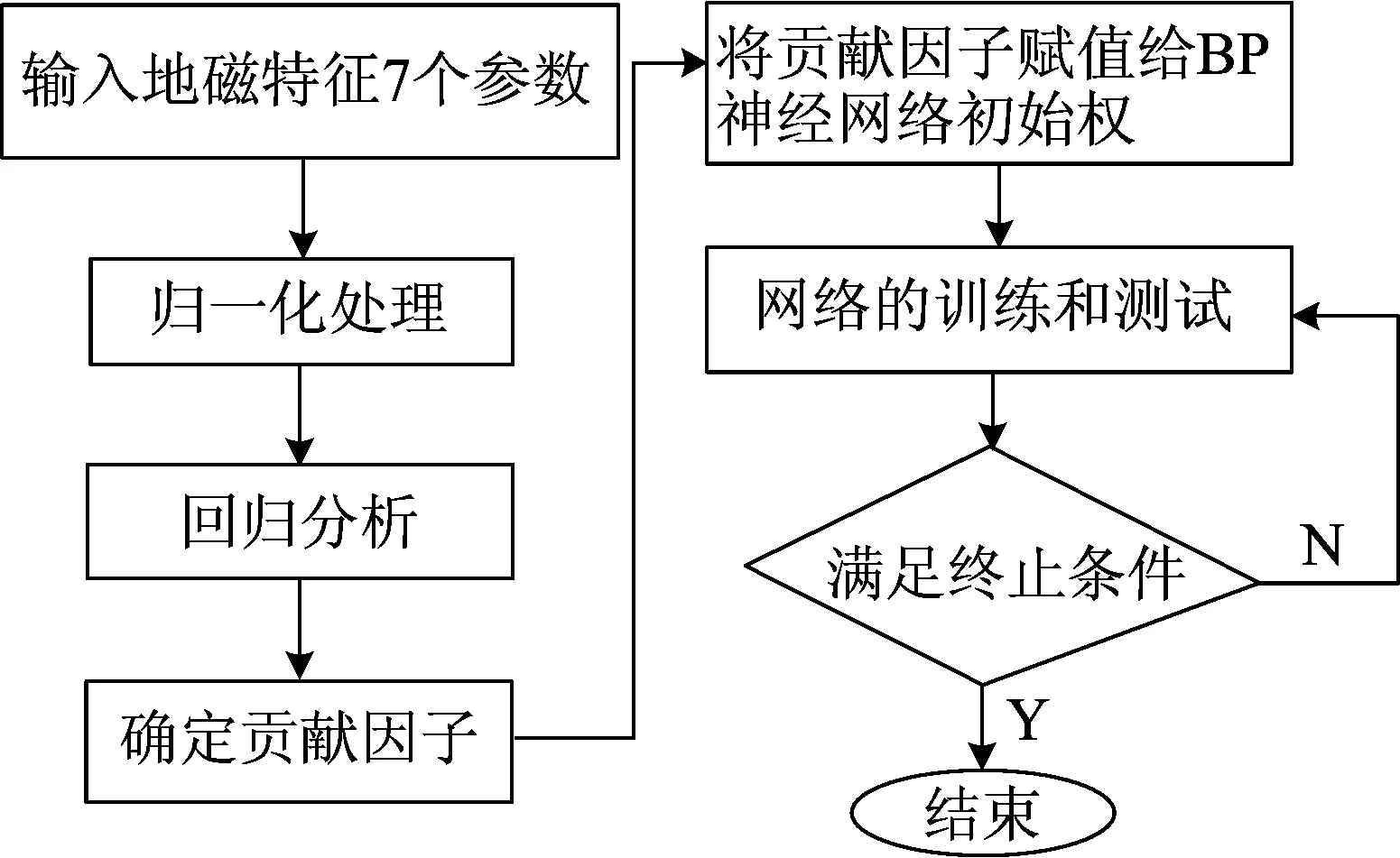
图3 数据处理流程

BP神经网络试验采用目前最先进的TensorFlow平台进行编程和优化。TensorFlow是谷歌基于DistBelief进行研发的第2代人工智能学习系统,为开源机器学习框架,具有快速、灵活并适合大规模应用等特点,能够解决各种机器学习任务。传统的判别方法采用基于Matlab的编程实现,最终将两者进行对比。

4 试验结果与分析

4.1 贡献因子

根据(2)式归一化地磁特征因子得到:

(4)

将F1～F7的取值代入(1)式计算可得:

P(F)=1.260-0.427F1-0.273F2-0.559F3+0.819F4-0.187F5-0.109F6-0.128F7

(5)

则有:

由(3)式可得：

(6)

由(6)式可得7个特征因子的wI,见表7所列。

表7 7个地磁特征因子对应的wI

从表7可以看出,在描述井下地磁特征的7个特征因子中,F3、F4对匹配概率的影响较大,其wI分别为22.3%、32.7%;F5、F6、F7对匹配概率的影响较小,wI均不到10.0%;F1、F2的wI分别为17.1%、10.9%。

4.2 参数设置

设置激活函数为relu函数,将隐藏层个数h分别设定为10、12、14、16、18进行对比试验,试验结果见表8所列。

表8 不同h下网络的准确率 %

由表8可知,随着h增加,模型在测试数据集上的准确率逐渐提高,在h=14、h=16时网络的准确率一样,而在h=16时出现拐点,因此初步确定h为14或16;在训练数据集上,随着h增加,模型的准确率逐渐提高,h=16时网络的准确率高于h=14时的网络。综合分析以上结果,设置h=16。

设定h=16,对比sigmoid、tanh、relu 3种激活函数下网络训练的准确率,结果见表9所列。从表9可以看出,3种激活函数对训练集和测试集数据的识别准确率是不同的。采用sigmoid函数的网络几乎不具备识别能力;采用tanh函数的网络识别能力一般;而采用relu函数的网络性能最好,其在训练数据集上的准确率高达95.0%,在测试数据集上的准确率达到了72.7%,试验结果充分证明了relu函数在该模型中的优势。

表9 3种激活函数下网络的准确率 %

4.3 适配性评价的对比分析

对试验数据分别采用传统贝叶斯判别、线性距离判别、二次函数判别以及普通BP神经网络和基于贡献因子BP神经网络进行适配性评价,将2种BP神经网络均随机训练5次,计算其平均准确率以减小网络陷入局部最优对识别准确率的影响,训练样本和测试样本的评价结果对比见表10所列。

表10 5种方法的适配性评价结果

由表10可知,在对地磁适配性评价中,二次函数判别法的识别准确率最低,训练数据准确率不到80%,测试数据准确率仅为45%左右;基于传统贝叶斯判别、线性距离判别的准确率较为接近,训练数据准确率均为80%左右,测试数据准确率仅为50%左右;基于贡献因子BP神经网络的准确率最高,训练数据准确率达到了95%,测试数据准确率接近73%,优势明显。相比于普通BP神经网络,改进后的网络能一定程度上避免陷入局部最优从而达到较高的识别精度,网络的收敛速度也有明显提升,但是基于贡献因子BP神经网络分析时,训练前期工作较多,工作量较大。

5 结 论

(1) 围绕地下工程地磁定位的区域适配性评价问题,综合分析了区域磁场空间特征因子与匹配概率相关性。根据地下工程的地磁空间分布特点,确立了地磁标准差、峰态系数、偏态系数、地磁粗糙度、粗糙方差比、地磁信息熵及相关系数7个地磁空间分布特征参数。

(2) 在BP神经网络基础上,设计了基于贡献因子BP神经网络适配性评价流程,建立7-h-1结构的地磁适配性BP神经网络,提出了贡献因子的计算方法。基于贡献因子BP神经网络的输入层为7个地磁空间分布特征因子,其初始权为回归分析后的贡献因子;输出层为按照匹配概率划分的适配等级,即强适配、适配、弱适配、不适配。

(3) 将贡献因子赋值为BP神经网络的初始权进行训练,使网络能够快速收敛并具有较高的识别精度。但是在实际应用中,样本数量和贡献因子计算需要进一步优化,模型的泛化能力也需要进一步提高。