一种新的鲁棒三维点云平面拟合方法

童子良, 余学祥, 汪 涛, 王 虎, 苏晓刚

(1.安徽理工大学 测绘学院,安徽 淮南 232001; 2.安徽理工大学 矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室,安徽 淮南 232001; 3.安徽理工大学 矿区环境与灾害协同监测煤炭行业工程研究中心,安徽 淮南 232001)

随着智慧城市、虚拟现实(virtual reality,VR)技术、人工智能(artificial intelligence,AI)、逆向工程等概念的出现,人们对空间三维信息的需求显得日益迫切,传统的获取数据的方法已经无法满足实时、高精度、可视化的要求。三维激光扫描技术又被称为三维实景复制技术,是测绘领域继GPS空间定位技术之后又一次技术革新,它的出现为空间三维信息的获取提供了全新的技术支持。与常规的观测方法相比,三维激光扫描技术具有以下优势:① 可以实现复杂三维数据的采集与处理,实时性强;② 可以快速组建目标的三维模型等多种数据;③ 无需与被测物体接触,可在恶劣环境下工作;④ 可以获取大量数据信息且精度较高[1]。因此,三维激光扫描技术已经在工程变形监测[2]、古建筑保护[3]、智慧城市建设[4]等领域获得广泛应用。

因为三维场景中有大量的平面特征,如墙面、道路、桥梁等等都是平面组成的,将扫描得到的点云数据拟合成平面,经过点云配准、去噪、简化之后可实现高精度地重建该物体的三维模型,所以点云的平面拟合是多数平面重建工程的重要组合部分。传统的拟合方法有经典的最小二乘法和特征值法。最小二乘法只考虑到观测向量中的误差,忽略了系数矩阵中的误差;而特征值法无法消除噪声对拟合过程的干扰,导致拟合平面的精度差,不具有鲁棒性。文献[5]提出了整体最小二乘的稳健点云拟合方法,虽然可以同时顾及观测向量和系数矩阵的误差,但是由于点云数据是不等精度的,并且存在大量的异常点,采用整体最小二乘法估计的参数也不是最优解;文献[6]提出了稳健加权总体最小二乘的点云平面拟合法,通过加权的方法先剔除异常点,再通过稳健总体最小二乘法求出参数解。虽然以上方法可以估计出平面的参数解,但是其算法编译复杂,解算效率低。近年来,一些研究者将主成分分析 (principal component analysis, PCA)方法应用到点云平面拟合和曲面拟合中,文献[7-8]研究表明拟合效果好,且算法编译简单。此外,随机采样一致(random sample consensus, RANSAC)算法可以用少量样本数据来评估模型参数,对错误率超过50%的数据仍然能得到理想的处理结果,是最有效的鲁棒估计方法[9-11]。本文提出采用RANSAC算法与PCA方法相结合,在拟合平面之前先用RANSAC算法对获取的点云数据进行预处理,然后通过PCA方法对预处理的点云数据进行重采样,从而达到消除粗差并增强鲁棒性的效果。

1 RANSAC算法

RANSAC是采用迭代的方式从一组包含离群的被观测数据中估算出数学模型参数的方法。该算法最早由Fischler和Bolles于1981年提出[12]。RANSAC算法中采集的样本为2类点云数据:① 内点数据(inliers),即符合算法模型的数据;② 异常数据,记为外点(outliers),为不符合模型所需的点。

RANSAC算法的基本原理[13]如下所述:

(1) 假设所有的点云数据集为Ω,从该点云数据中选取一个符合模型条件要求的最小样本数为n(n≥3,因为至少3个点才能构成一个平面)的最小样本子集,利用最小二乘法计算出最小样本子集所对应的模型参数,并作为初始化模型参数,接着计算Ω所有点集数据与初始参数之间的差值,根据已经设定好的阈值T,当该差值小于设定的阈值,则将该样本点归为模型内点,反之即视为不符合模型所需点将其剔除,记录此时的内点数。

(2) 重复以上过程,获得更多的内点与最佳模型参数。根据实际情况设定迭代次数K,当迭代结束时,计算出的最佳模型参数即为最佳估计参数。

(3) RANSAC算法要求在一定的置信概率下,其中n与至少获得1个良性取样子集的概率Q(Q>ε)满足的关系式为:

Q=1-[1-(1-ε)n]K

(1)

其中,ε为样本污染率。K的计算公式为:

(2)

一般情况下,ε、Q均会根据实际情况给定。

2 PCA方法

PCA作为一种多元统计技术,是由美国统计学家Pearson首次提出的。它从多指标分析出发,运用统计分析原理提取少数几个彼此不相关的综合指标并且能够保证原指标所提供的大量信息,通过原来变量的少数几个线性组合来解释原来变量绝大多数的信息。具体来说,它利用降维思想构造了原始数据的一个正交变换,新空间的基底去除了原始空间基底下数据的相关性,通过线性变化,将原始数据集变化为一组各维度线性无关的表示,这些新的基底即为主成分。目前,PCA方法广泛地应用在图像识别[14]、图像处理[15]、特征信息提取[16]等领域。

本文PCA方法推导如下所述。

假设采样点拟合的切平面目标函数为:

ax+by+cz=d

(3)

其中，n=(a,b,c)为单位法向量,且满足:

a2+b2+c2=1, ‖n‖=1

(4)

按照上述准则,各个采样点Pi到切平面的距离要尽可能小,目标函数为:

(5)

其中,xi、yi、zi为采样点坐标;N为采样点个数。该问题可转化为求解极值问题,即

λ|a2+b2+c2-1|)

(6)

其中,λ为待定参数。由(6)式将目标函数改写为:

(7)

(8)

对J求偏导得到:

(9)

将(9)式整理后可得:

(10)

对(10)式进行特征分解,将矩阵变换为对称正定矩阵,故有3个实特征值λ0、λ1、λ2,由此求得它们所对应的特征向量为v0、v1、v2。

上述即为PCA标准推导过程,在优化目标函数时,为所需的采样点拟合一个平面,最大可能地确保它们都在平面上,即点到平面的距离最小,因此取最小特征值λ0的特征向量v0作为采样点的法向量。根据求得的法向量得到所求的最佳拟合平面。

3 本文点云拟合新方法

本文为了提高拟合精度,首先在选取预处理点时设置阈值,以保证拟合平面点的“纯度”,然后采用点到平面距离的标准差为拟合平面的精度,标准差越小,拟合点之间的分散程度越小,拟合效果越好;反之则越差。采用RANSAC算法在迭代过程消除点云数据中的粗差值,使得点云中的异常值大幅减少,然后利用PCA方法的降维思想对预处理的采样点数据进行重采样,达到二次拟合的效果。将RANSAC算法和PCA方法结合起来的点云拟合步骤如下:

(1) 根据给定的ε、Q及n,通过(2)式计算最小迭代次数K。

(2) 从所有的采样点数中随机选取m个点(m>3),利用(3)式和步骤(1)中给定的参数计算平面模型参数的初始值。

(3) 根据平面参数的初始值,计算允许值α,若该允许值在给定的阈值内,即为内点,反之为噪声点。

(4) 重复步骤(2) 、步骤(3),迭代K次,将内点归为一类,并统计其数量,数量最多的点集作为预处理点集。

(5) 利用PCA方法根据RANSAC算法得到的预处理点集,计算平面的法向量n(a,b,c)。

(6) 计算所有采样点到目标平面的距离,计算公式为:

(11)

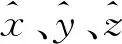
(7) 求出di的标准差δ,计算公式为:

(12)

(13)

(8) 当di>2δ时,认为该点为噪声点,否则保留该点。

(9) 重复步骤(1) ～步骤(4),进行K次迭代,直到所有点都在阈值范围之内。

(10) 得到最佳拟合平面方程。

4 实验分析

4.1 仿真实验

采用仿真实验数据对本文方法进行验证,并与最小二乘法、特征值法拟合结果作对比。设需要拟合的空间平面方程为:

(15)

通过Matlab从已知平面随机选取1 000个点,该数据为未受到异常值污染情况下的仿真数据,如图1所示;在上述仿真数据中加入50个噪声点,如图2所示。使用最小二乘法、特征值法及本文方法对图1、图2的仿真数据进行参数估计,并计算δ,结果见表1、表2所列。表1、表2中,括号里的数据为设定的参数值。

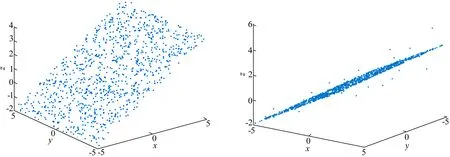
图1 不包含噪声点的仿真数据 图2 包含50个噪声点的仿真数据

表1 未加入异常值的仿真实验参数估计结果

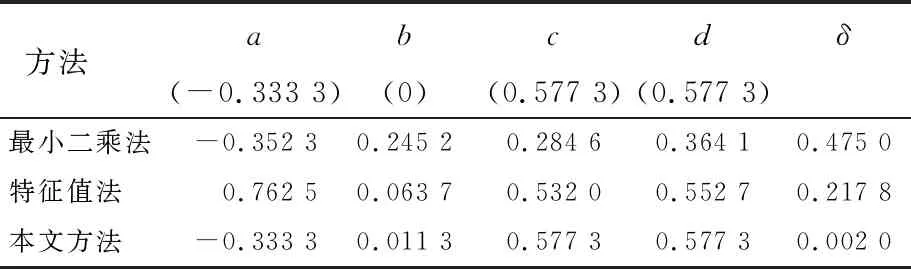
表2 加入50个异常点的仿真实验参数估计结果

虽然数据是随机抽取的,每次运行的结果可能会有一些小的差别,但由表1、表2可知,当数据不存在异常值时,虽然3种方法的平面拟合参数值都十分近似,都接近预设的参数值,而本文方法进行预处理后的点云数据离散程度更低,故拟合后的效果更好,其δ为2.457 2×10-17,低于最小二乘法和特征值法的δ值,说明在进行拟合之前,对采样的点云数据进行预处理是十分必要的;加入一些异常点后,最小二乘法和特征值法得出的估计参数值与设定的参数值之间存在很大的误差,而本文方法的δ为0.002 0,远远低于前2种方法的δ值0.475 0、0.217 8,故拟合效果极佳。本文方法所得估计值与预设值十分接近,由此可知本文方法稳定且精度高,具有鲁棒性。

4.2 实例分析

为了进一步检验本文方法在点云平面拟合中的可行性,通过采样实体建筑物的实测点云数据进行验证。实验采用中海达HS650高精度三维激光扫描仪,该仪器采用脉冲式的测距方式,可多次回波输入,其激光发散性小于等于0.35 mrad,最大测程达到650 m,测距精度为5 mm至100 m,全景分辨率大于7 000×104像素。

以安徽理工大学测绘学院大门的点云数据为测试实例,如图3所示。由图3可知,该模型具有大量的平面特征信息,故手动提取位于同一平面特征上的点云数据,如图4所示。

分别采用最小二乘法、特征值法和本文方法对实测的点云数据进行平面拟合,结果见表3所列。从表3可以看出,当实测的点云数据中不含有噪声点时,3种方法拟合的参数值大致相同,最小二乘法的精度稍低,特征值法与本文方法的δ较小,拟合精确性较高。当点云数据混入噪声点时,以表3中3种方法得到模型参数的平均值作为此平面的参考值,此时的噪声点与原始点云数据不处于同一平面上,即这些噪声点到原始点云拟合平面的距离超过了所设定的阈值范围,此时通过3种方法对点云数据进行处理,所得结果见表4所列。由表4可知,当点云数据中混入噪声点时,传统方法拟合精度较低,通过前2种方法计算的δ分别为0.029 0、0.013 8,远大于本文方法得出的9.375 6×10-4。由此可知,本文方法不仅可以去除噪声点,而且拟合平面参数值与参考值之间的偏差极小,精度和稳定性都高。

图3 测绘学院大门点云数据

图4 处于同一平面上的点云数据

表3 不含噪声点时3种方法估计的实测数据参数

表4 包含噪声点时3种方法估计的实测数据参数

5 结 论

通过三维激光扫描仪采样时,由于环境、仪器等各种因素的限制,获取的点云数据不可避免地存在异常值或者粗差,而传统的最小二乘法和特征值法没有考虑这些噪声点对于拟合精度和准确度的影响。针对以上问题,本文提出采用RANSAC算法与PCA方法相结合的方法,在拟合平面之前先用RANSAC算法对获取的点云数据进行预处理,先去除一部分的粗差点,然后通过PCA方法对预处理的点云数据进行拟合,从而达到消除粗差并增强鲁棒性的效果。通过仿真实验和工程实例进行了验证,实测实验结果表明采用本文方法得出的标准差为9.375 6×10-4,远远低于传统的方法得出的标准差,由此可知通过本文方法可以得到更加精确的拟合平面, 本文方法具有更好的适用性。