基于线性滤波法的超高层建筑脉动风速时程模拟
2020-12-30郭小飞
常 乐 郭小飞
(1.中国建筑科学研究院有限公司,北京 100013;2.石家庄铁道大学土木工程学院,河北 石家庄 050043)
0 引言
近些年,随着轻质高强材料、新技术在土建工程中的广泛应用,高层建筑结构不断向着柔度更大、阻尼更小和基本自振周期增大的方向发展,致使结构的自振频率更加接近于风荷载的卓越频率,尤其是超高层建筑对风荷载具有较强的敏感性。目前,对于风敏感的复杂超高层建筑风振响应分析方法有频域法和时域法两种[1]。频域法只适用于线性结构分析,不能考虑结构几何、材料等的非线性影响;而时域法能够克服频域法的不足,结构的加速度、位移和力的最大值可以直接得出。虽然时域法比频域法分析时较为复杂,需要耗费更多的时间与精力,但是随着计算机科学技术的飞跃发展,时域法使用起来已经不再困难。采用时域法对结构进行风振响应分析时,关键是建立随机过程的时域模型[2]。目前,脉动风速时程模拟方法有两种:线性滤波法和谐波叠加法[3-5]。近年来,白噪声滤波法中的 AR 模型能有效地考虑脉动风速的随机性、时间相关性及空间相关性,并且占用计算机内存较少、计算效率高、应用较广。
1 风的特性
风对结构的作用主要由两部分组成:平均风作用和脉动风作用。从许多近地面风速时程实测文献中可以看出,平均风在给定的时间间隔内,风对建筑结构的作用力的大小、方向是不随时间改变的,在实际结构分析中将这部分力当作静力来计算。脉动风是由自然风的不规则性引起的,是随机性荷载。由于它的周期比较短(几秒钟至几十秒),接近于结构的卓越周期,因而应按动力来分析。
1.1 平均风特性
大气边界层内的平均风特性主要包含对场地基本风速大小的确定、平均风速的风向测量及平均风速沿着高度的变化规律等。Davenport 依据多个国家 90 多次的现场实测数据,运用理论推导和经验修正总结出了不同场地下的风速轮廓,提出了平均风速沿着高度变化的指数律模型[6],如式(1)所示。

式中:z 为结构的任一高度,m;v(z)为结构任一高度处的平均风速,m/s;zc为标准参考高度,m(通常为 10 m);vc为标准参考高度处的平均风速,m/s;α 为地面粗糙度指数。
1.2 脉动风速功率谱
工程上常用的脉动风速谱有 Davenport 谱、Harris谱、Karman 谱及 Kaimal 谱等,本文采用 Davenport 脉动风速谱,表达式如式(2)所示[7]。

式中:Sv(n)为脉动风速功率谱;n 为频率;K 为地面粗糙度系数。
2 线性滤波法中的AR模型
2.1 AR(p)模型的概念
AR(p)模型又名自回归模型,其表达式如式(3)所示[8]。

式中:β=[β1,β2,…,βp]T 为 AR(p)模型的自回归系数;θi为白噪声序列。
2.2 AR(p)模型阶数的确定
采用 AR 模型模拟脉动风速最重要的一方面是选择合理的阶数 p。作为一般性原则,如果选择的模型阶数太低,将会得到一个高度平滑谱。另外,如果 p 选择的太高,则会冒险在谱中摄入假的低峰。因此,本文选择比较公认的 AIC 准则来确定 AR 模型的阶数,该方法是通过选择合适的阶数使其达到最小化,表达式如式(4)所示。

式中:p 为AR模型阶数;N 为总的样本数;σ^2p 为线性预测误差的估计方差。
2.3 脉动风速时程模拟过程
M 个点空间相关脉动风速时程V(X,Y,Z,t)的 AR 模型如式(5)所示[9-10]。
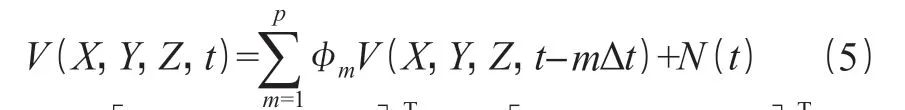
式中:X=[x1,x2,…,xM]T;Y=[y1,y2,…,yM]T;Z=[z1,z2,…,zM]T;(xi,yi,zi)为空间第 i 点坐标,i=1,2,…,M;p 为 AR 模型模拟阶数;Δt 为 AR 模型风速时程的时间步长;φm为 AR 模型的自回归系数矩阵,且为 M×M 阶方阵,m=1,2,…,p;N(t)为 M 维独立的随机过程向量,如式(6)所示。

式中:n(t)=[n1(t),…,nM(t)]T,ni(t)是相互独立的均值为 0、且方差为 1 的正态随机过程,i=1,2,…M;L 是 M 阶下三角形矩阵,通过 M×M 阶协方差矩阵RN的 Cholesky 分解确定,如式(7)所示。

为使以下公式简单明了,均将 V(X,Y,Z,t)简写为V(t)。将(5)式两边同时乘以 VT(t-jΔt),并作数学期望得式(8)。
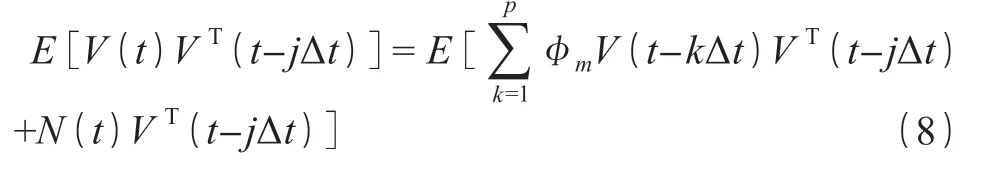
式中:j=0,1,…,p。
由自相关函数的性质:R(-jΔt)=E[V(t)VT(t-jΔt)]及 R(-jΔt)=R(jΔt),式(8)可得:
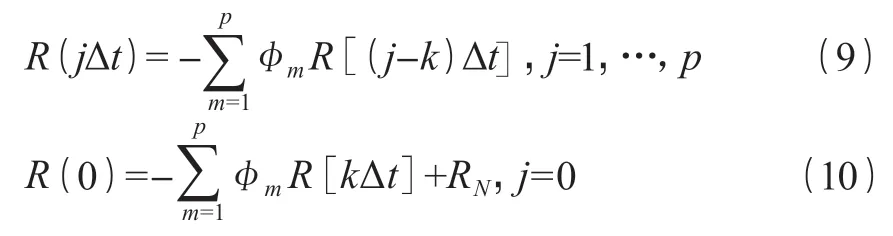
整理可得:

式中:φ=[I,φ1,φ2,…,φP]T,为(p+1)M×M 阶矩阵,I 为 M 阶单位矩阵;RN为 M×M 阶矩阵;OP为pM×M 阶矩阵,其元素皆为 0;R 为(p+1)M×(p+1)M阶相关函数 Toeplitz 矩阵,R 中的元素可由维纳-辛钦公式求出:
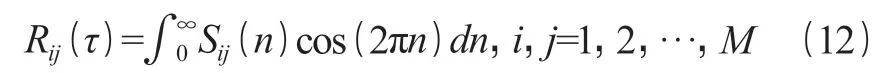
式中:Sij(n)当 i=j 时为脉动风速自谱密度函数;当 i≠j 时为脉动风速互谱密度函数,可由脉动风速的自谱密度函数 Sii(n)和空间相干函数 rij(n)确定,i=1,2,…,M; j=1,2,…,M。
空间任意两点相干函数 rij(n)的表达式可采用:
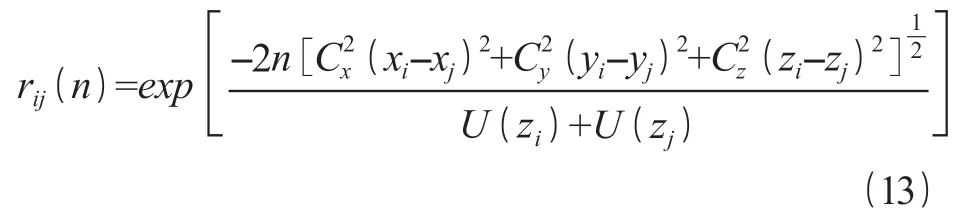
式中:|xi-xj|为空间两点 i 和 j 间的水平距离;|zi-zj|为空间两点 i 和 j 的竖直距离;|yi-yj|为纵向空间两点 i 和 j 纵向距离;U(zi)和 U(zj)分别为空间两点 i 和 j 位置 z 高度处的平均风速。Cx、Cy、Cz分别为横向、纵向、竖向的衰减系数,一般由试验确定,依据经验可分别取 16、8、10。
3 Bartlett 经典功率谱估计方法
Bartlett 法(又称为平均周期图法)是将 N 点样本序列 x(n)划分为 K 个子段,每段的长度有 M 个样本,也即 N=KM,如式(14)所示。

计算每一段的周期图,得出:
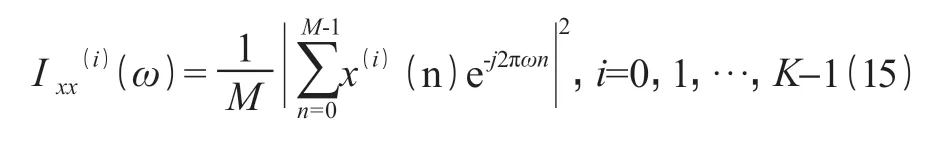
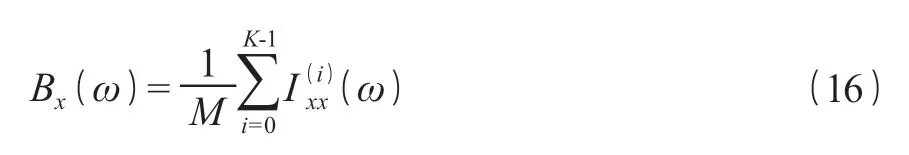
釆用快速傅里叶变换法能较为便捷地实现 Bartlett 法对功率谱的估计,并可以利用许多个点求解 x(i)(n)的周期图。由于 K 的增加,使得平均周期图 Bx(ω)的方差越来越小,因此它可以认为是功率谱的一种渐进一致估计。另外,因为该方法引用了平均值概念,由此减小了功率谱估计的误差及估计曲线的上下波动性,所以使用 Bartlett 法要比传统的周期图法结果更为平滑。
4 工程实例应用
4.1 工程概况
该超高层建筑位于武昌滨江商务区绿地集团国际金融服务长江流域中心地块上,地处武昌滨江商务区中心地区。该超高层建筑是一个集办公、公寓、写字楼、高档商场及会所等于一体的综合体项目,共有 100 层,高471 m,建筑效果图如图 1 所示。

图1 建筑效果图
4.2 脉动风速时程模拟结果
由于该建筑结构的楼层数量较多,如果在建筑结构的每一层都施加模拟的脉动风荷载将会比较繁琐,也是没有必要的,因此在保证工程计算精度的基础上将计算模型进行合理的简化,会使计算速度加快并减小工作量。所以本文利用 ETABS 软件建立了该主塔的有限元模型,依据有限元模型的模态分析结果,将模型简化为 28 个集中质量点,其中 1~40 层每 5 层简化成一个节点,41~100 层每 3 层简化为一个节点。某超高层简化模型节点划分如表 1 所示。本文采用上述 3 节介绍的线性滤波法中的 AR 模型,并采取 MATLAB 工具编写程序。分别生成了结构高度竖直方向上各节点处的脉动风速时程,脉动风速模拟时的具体参数如表 2 所示。
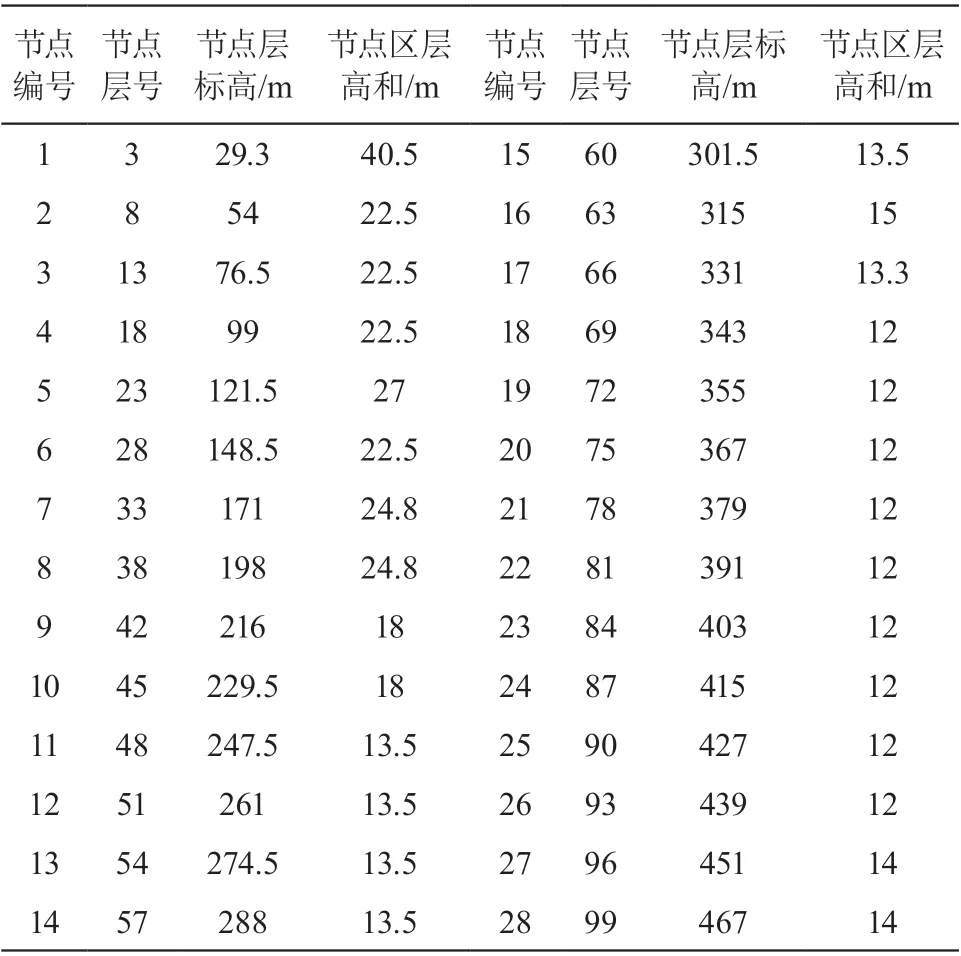
表1 某超高层简化模型节点划分

表2 脉动风速模拟的具体参数
本文分别选取 Davenport 经典脉动风速谱对该超高建筑结构进行了脉动风速时程模拟。限于篇幅,本文只选取了几个有代表性的节点作为研究,图 2 为模拟得到的脉动风速时程。由此可以看出,利用 AR 模型模拟出的各节点处的脉动风速基本都在 -11~12 m/s 变化,不同节点处的脉动风速改变规律也不一样,并且各节点处的脉动风速随着时间和空间的改变表现出了很大的随机性,这充分说明了脉动风之间的时间相关性与空间相关性。
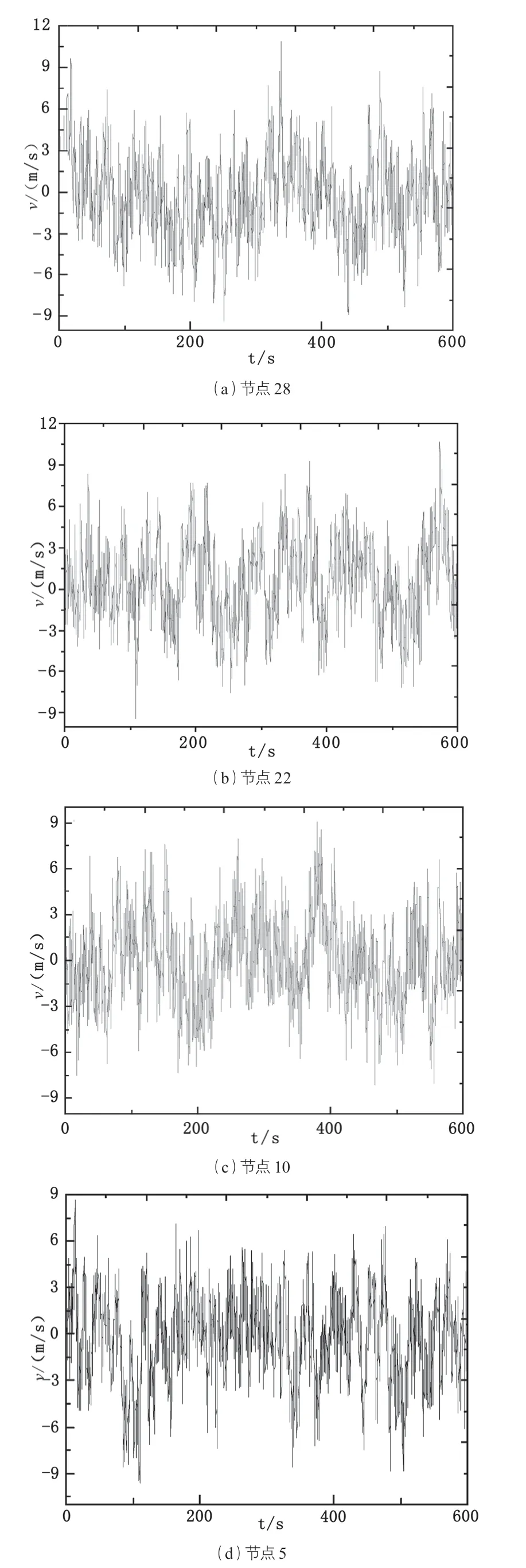
图2 Davenport 脉动风速谱对应的脉动风速时程曲线
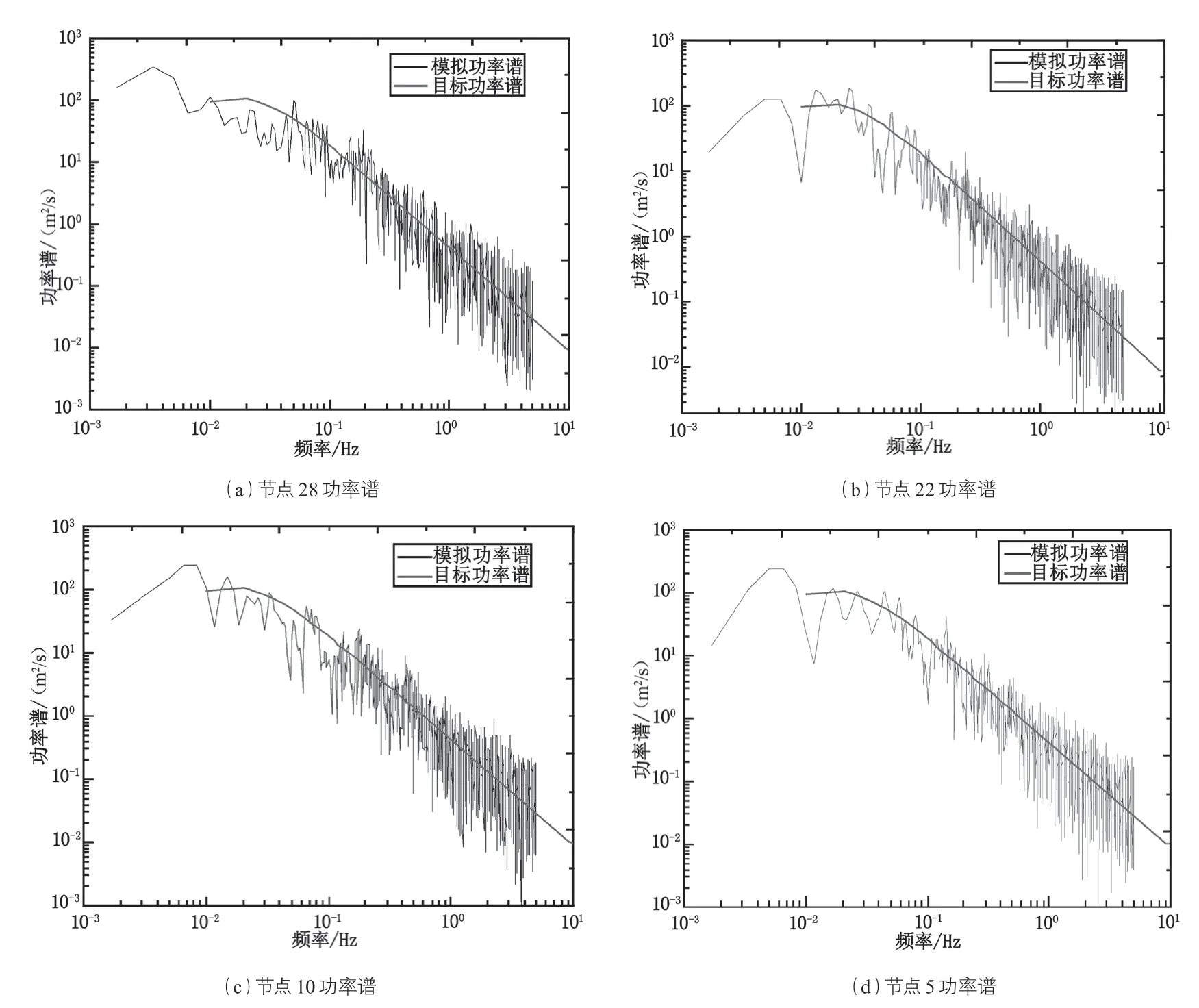
图3 Bartlett 法估计 100 年回归期 Davenport 脉动风速功率谱
为了验证模拟的脉动风速是否有效,需要将模拟得到的脉动风速功率谱与目标谱(Davenport谱)进行比对,本文选用第 3 章介绍的 Bartlett 法进行功率谱的估计,并通过在 MATLAB 软件中利用 PSD 函数编写相应的程序来实现功率谱评估。图 3 为 Bartlett 法估计 100 年回归期 Davenport 脉动风速功率谱。从图 3 可以看出,模拟的功率谱曲线与目标功率谱曲线趋势基本吻合,说明 AR 模型模拟风速时程算法的有效性,可以用于实际结构的风振响应时程分析。
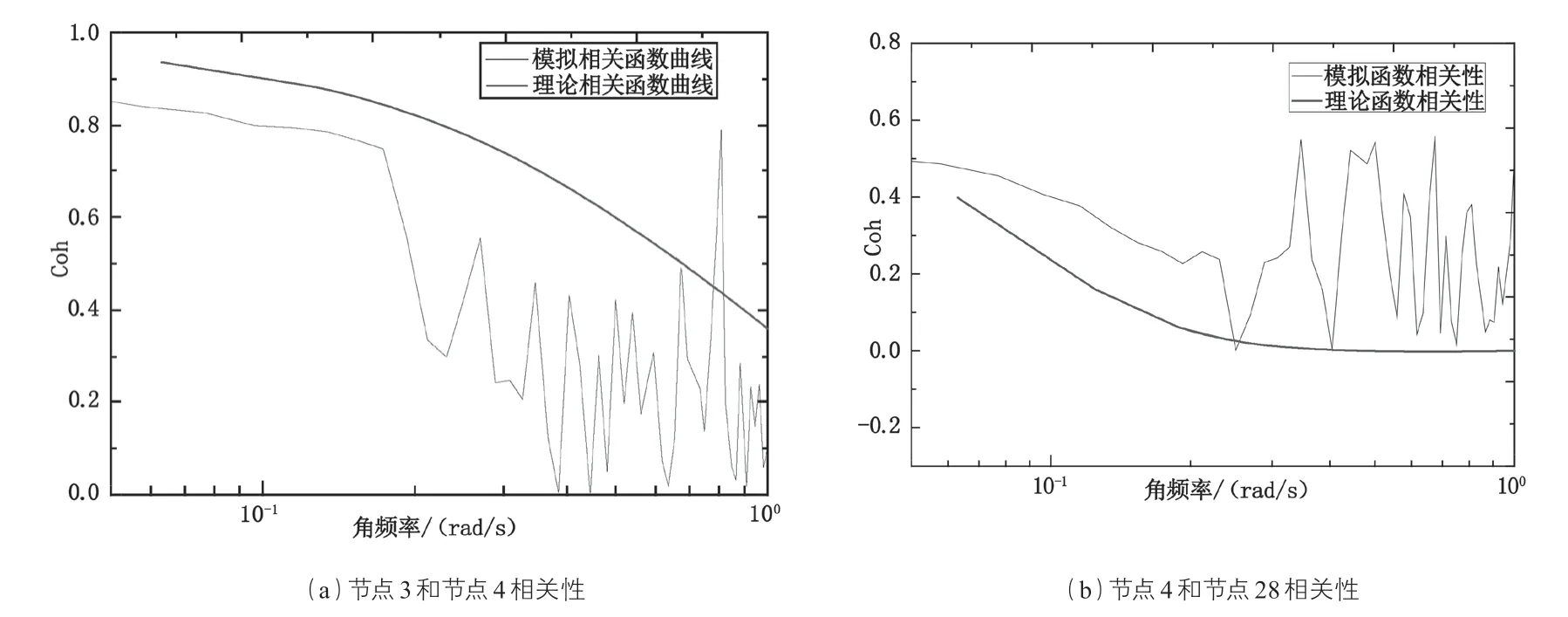
图4 100 年回归期 Davenport 脉动风速的相干函数估计
另外,还需要检验各节点之间的空间相干性。本文运用 MATLAB 程序中的 mscohere 函数来评估空间节点之间的相干性。图 4 为模拟脉动风速时程的相干函数曲线与目标函数曲线的对比。由此可以看出,模拟出的各节点之间的脉动风速空间相关性曲线与采用的理论模型相关曲线在较低频率处(0~0.2 Hz)吻合度很好,但在频率大于 0.2 Hz 高频部分相差较大,而由于在高频区时的脉动风速分量较少,并且远离结构的自振频率,所以由此引起的误差对结构的风振响应时程分析结果的影响很小。
5 结论
本文介绍了风的基本特性,并以某超高层建筑为工程背景,采用线性滤波法中的 AR 模型模拟生成了作用于结构上各个节点的脉动风速时程。研究结果表明:AR 模型模拟的脉动风速效果较好,模拟精度高,模拟得到的脉动风速谱与目标谱基本吻合,可以作为结构风振响应时程分析的荷载模式输入。
