面向时变需求的高铁快运专列时刻表和配装方案综合优化研究*

高如虎 牛惠民 杨喜梅

（兰州交通大学交通运输学院 兰州730070）

0 引 言

为充分发挥高铁运力资源优势和快递公司的两端服务网络优势，加快推动“高铁网+快递网”双网深度融合，全面深化铁路运输供给侧结构性改革，一些服务多元、衔接紧密、时效严格的高铁快运产品被相继推出。尤其是以中铁快运股份有限公司与顺丰速运有限公司联合推出的“高铁极速达”快运产品为代表[1]。此类快运产品以高铁动车组为载体，通过快递公司收派端快速驳接网络衔接高速铁路优质稳定的极速运力，为客户提供指定服务范围、承诺运到时限的高端快运服务。

高铁快运主要利用高铁确认车、载客动车组、预留车厢、快运专列等运力资源对快件包裹提供快捷的站到站服务[2]。其中，载客动车组、高铁确认车、预留车厢所对应的列车均为图定列车，其列车时刻表已经确定。并且在铁路运输中，客运服务相较于货物运输具有较高的优先权，因而，在利用此类列车组织货物快运时，一般不对列车时刻表进行调整。电子商务驱动下，尤其一些购物节（如“双十一”“双十二”“六一八”等）疯狂购物的背后，第三方物流企业迎来了空前的快件包裹量。这时，高铁快运需求激增，图定列车的能力不能满足增长的快运需求，需要增开快运专列以提高服务质量。

当增开快运专列时，在图定的列车时刻表确定的条件下，需要编制新增快运专列时刻表。若靠传统的手工编制，一方面难以保证时刻表的质量，另一方面无疑增加了调度人员的工作负担。现有对列车时刻表的研究大体可以分为2 类，一类是仅从铁路运营者的角度出发，不考虑需求条件下的列车时刻表优化。文献[3-5]均以列车旅行时间为优化目标，建立了列车时刻表的混合整数规划模型，其中，文献[3-4]提出了拉格朗日松弛算法对问题求解，文献[5]利用分支定界算法对问题求解。为了从本质上揭示铁路运输需求与运输服务供给的耦合关系，提高铁路客货运服务质量。另一类从需求角度出发，对需求驱动下的列车时刻表进行研究。文献[6]在时变客流需求条件下，以乘客在站等待时间为优化目标，构建了列车时刻表和列车停站方案的非线性整数规划模型，并利用通用求解软件GAMS对模型求解。文献[7]对越行许可条件下基于时变客流需求的列车时刻表进行优化，并分别建立了定序无越行、定序有限越行及非定序任意越行3 种数学模型，利用通用求解器CPLEX对模型求解。文献[8]旨在优化动态客流驱动下的列车时刻表，并综合考虑了列车能耗问题。文献[9]以需求为响应，构建了铁路集装箱班列始发时刻优化模型，充分考虑了集装箱与集装箱班列在时间和数量方面的匹配关系，并利用遗传算法对模型求解。

货物配装是铁路货物运输过程中的一个重要环节，配装方案对货物的运输效率、运到期限有重要影响[10]。高铁快运配装方案优化问题旨在对专用快运箱的配装时间和配装列车进行决策，以期提高快件的运到时限和运输效率。现高铁快运配装方案主要靠车站工作人员根据快运箱的到达情况手工编制。这种传统的编制方法一方面难以保证配装效率，另一方面可能导致某些快运箱长时间“压仓”。随着高铁快运需求的进一步增长，需要对快运箱的装配方案优化决策，而目前鲜有文献对此深入研究。值得说明的是，列车时刻表决定了快运箱的配装时间和途中运输时间，进而影响配装列车的选择。在需求驱动条件下，高铁快运配装方案和列车时刻表关系密切，需对二者综合优化。

高铁快运作为一种新兴的快运方式，正受到前所未有的关注。目前大多文献主要从快运模式、作业流程、市场机遇等宏观方面进行探讨[11-12]。而鲜有文献从运输组织优化的角度对高铁快运进行研究。与现有相关文献相比，本文的创新点如下。

1） 试图从运输组织优化的视角出发，对高铁快运列车时刻表和配装方案综合优化，完善高铁快运服务网络设计理论，以期提高高铁快运的运输效率。

2） 以是否增开快运列车为研究问题的切入点，在需求驱动条件下，分别构建了与阶段计划相切合的分阶段优化的无新增快运专列的配装方案优化模型和新增专列时刻表和配装方案综合优化模型。

3） 在模型线性化的基础上，利用通用求解器CPLEX对模型精确求解，并通过实例验证了本文模型的正确性和求解方法的有效性。

1 问题分析及说明

1.1 高铁快运产品分析

高铁快运产品主要针对紧急寄递需求的商务信函、标书合同、个人紧急物品、生鲜礼品、电商中小件包裹、行包类等高附加值货物。目前，高铁快运服务已在高铁路网中多条线路经停的车站运行或试运行，服务范围基本实现了直辖市、省会城市和经济发达县域全覆盖。

高铁快运产品作业流程见图1。由于铁路部门在“门到门”“最后一公里”服务方面能力还较为薄弱，高铁快运产品目前只提供“站到站”的服务，快件的收发和配送作业由第三方快递企业收派点完成。收派点按照快件的目的地分类将快件装入铁路部门指定或者提供的专用快运箱，统一送往对应高铁车站。铁路调度部门根据高铁线路（区段）各个车站收到的快运箱需求统一编制运输服务方案，并将编制的快运专列时刻表和配装方案下达至各高铁车站，各车站根据接收的列车时刻表和配装方案组织实施装车。快运箱运达对应车站后，车站人员进行卸车、拆包分拣作业，并在指定地点与第三方快递企业接驳人员进行交接。

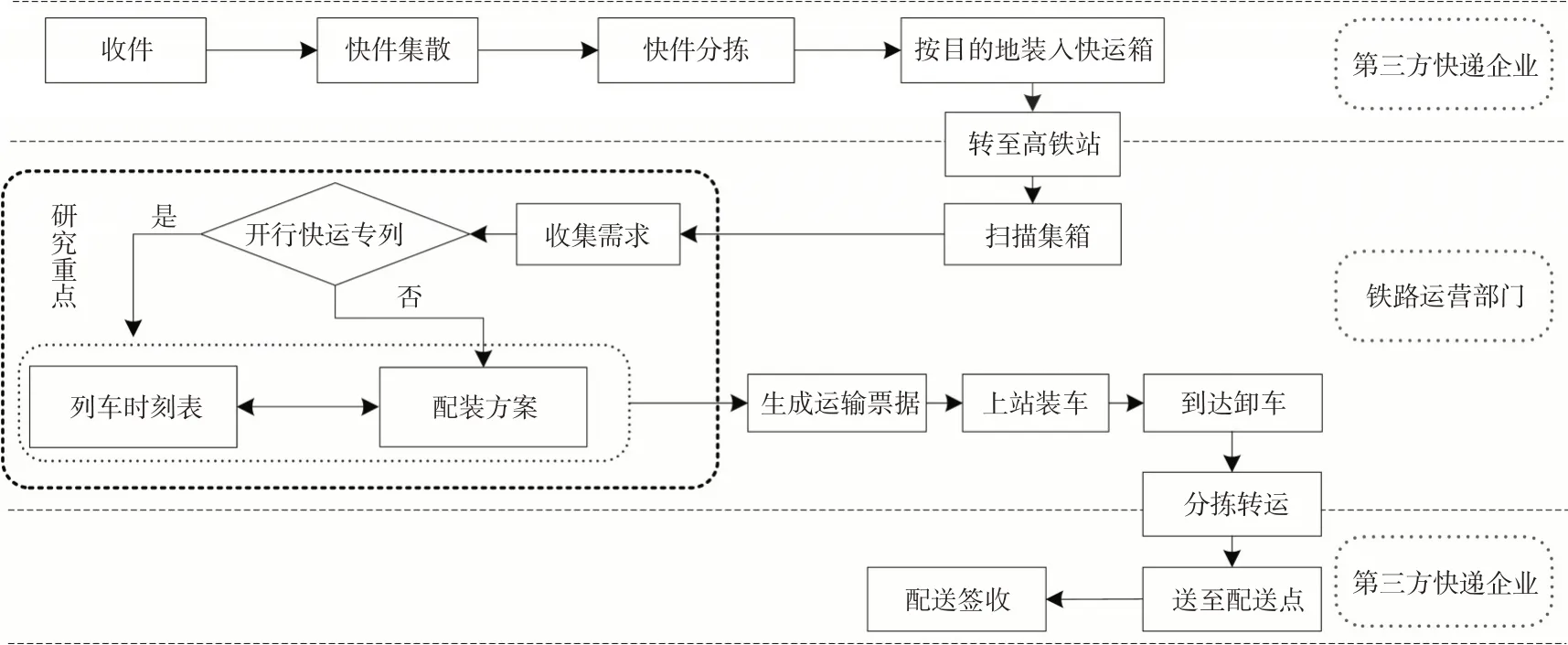
图1 高铁快运作业流程Fig. 1 Operation process of high-speed railway immediate delivery

1.2 问题分析及假设

本文以单条高铁线路为研究对象，按照运输生产实际，线路2个方向列车相互独立运行，选取其中的1 个方向进行研究。沿着该线路列车运行方向，车站集合定义为U ={1,2,…,n}。其中:1 为始发站；n 为终点站。我国铁路列车时刻表的精确度为1 min，因而按照1 min为间隔对运营时段进行离散处理，以1 min 的整数倍表示列车在车站的到发时刻和在区间的运行时间。快运箱运达车站的时间可能不是整数分钟，本文将其向下取整，将快运箱运达车站的时间也精确到分钟，这种近似处理不会影响优化结果。

事实上，铁路部门按阶段计划组织快运列车和配装运箱，见图2。事实上，这种按阶段计划的铁路运输调度问题称为“列车运行调整”，但列车运行调整也属于列车时刻表问题的范畴。为便于描述，本文将研究问题界定为高铁快运专列时刻表优化问题。本文将全天运营时段按照3～4 h均分为多个阶段，这与铁路运营的阶段计划（调整计划）相切合，本文以3 h 为1 个阶段。在第q + 1 阶段开始之前，根据前一阶段q 到达各车站的快运箱及阶段q 之前滞留的快运箱驱动优化第q + 1 阶段的配装方案和列车时刻表。每个阶段快运箱配装方案和快运专列列车时刻表的优化方法均相同。因而，后文中所定义的符号和建立的模型都是针对某一阶段的。这种按阶段计划的分阶段的方法可以减少快运箱在车站的等待时间，满足高铁快运产品当日达、次晨达、次日达的快运需求。

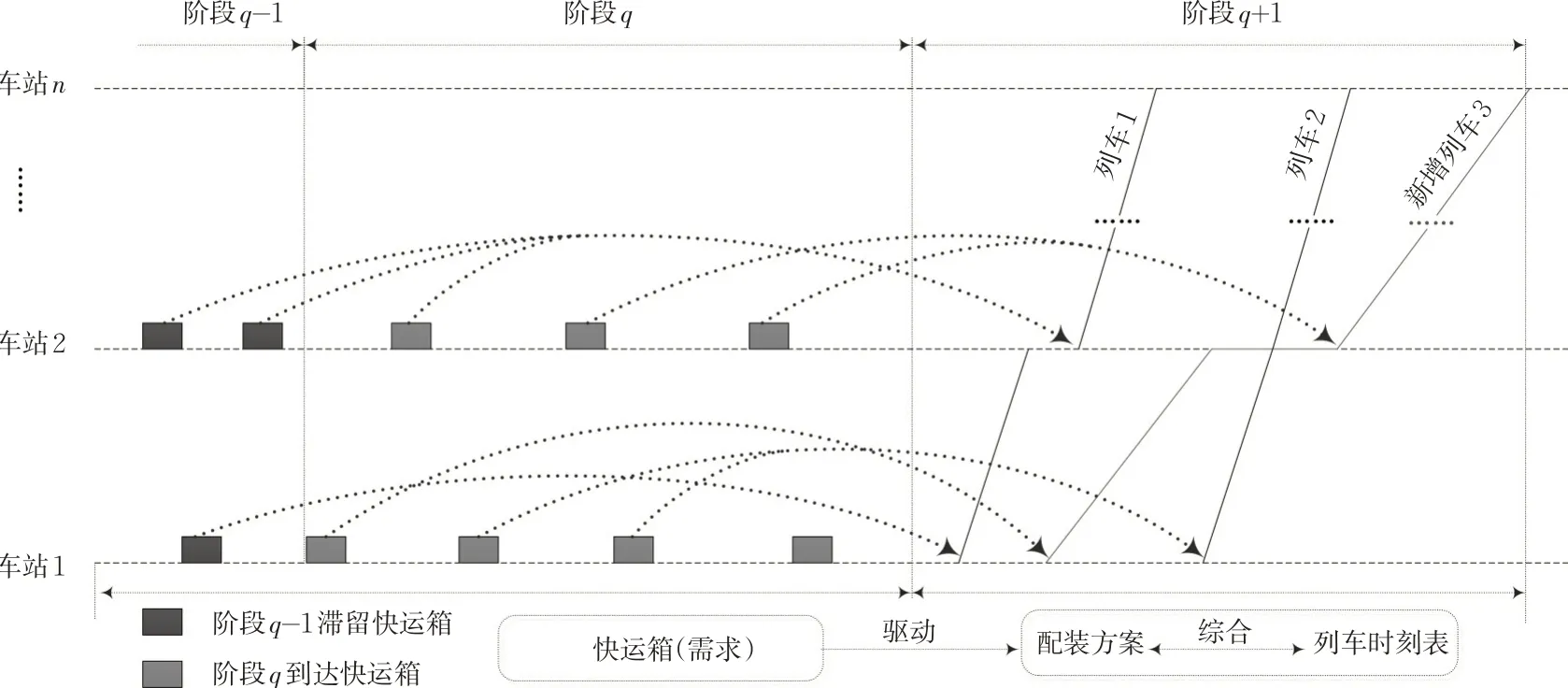
图2 按阶段的需求与配装方案和列车时刻表的关系Fig. 2 Illustration of relationship for the phase-based demand with assignment plan and train timetable

在时变需求条件下，每分钟到达车站的快运箱需求是不均衡的，根据这种动态时变的需求安排列车服务供给并将其指派在具体列车上，如何匹配离散的客流需求与列车运行线是构模的关键，也是本研究的难点。此外由于列车时刻表本身的组合特性，本质上属于NP-hard问题，使得问题精确求解异常复杂。值得说明的是，在时变需求条件下，可分为需求分布确定与需求分布不确定2 种研究思路，根据这种分阶段优化方法，本文的研究属于需求分布确定的情况，而需求分布不确定的研究是将来作者的研究方向。根据需求与服务供给之间的匹配关系可分为2种情况。一种是当每列车的能力均能满足需求时，即每列车从车站发出时，车站再无滞留需求，这时，最优的配装方案为“先到先上车”。而高铁快运产品的需求属于另一种是先于本阶段列车运达车站的，当列车出发后有快运箱滞留，这相当于铁路客运客流需求过饱和（超拥挤）的情况[13]，此时，需要根据优化目标和快运箱需求决策最优的装配方案。

为方便模型建立，本文作出如下假设。

1） 本文研究核心是列车时刻表及配装方案，而列车开行数量和列车停站方案均属于列车开行方案的范畴。假设列车开行方案确定是研究列车时刻表问题的一种普遍做法[13-14]。基于此，本文假定阶段内增开快运专列的数量及停站方案根据需求分布预先确定，并且给定快运专列的最小和最大停站时间，列车在该范围内灵活的选择停站时间。对于列车开行数量及停站方案不确定的情况是作者未来的研究方向。

2） 假设新增快运专列可被图定列车越行。

1.3 符号说明

在研究的阶段内，定义的各类集合、索引、参数、变量如下。

1） 集合。 Ie为图定列车集合；Iz为新增的高铁快运专列集合；I 为所有列车集合，I = Ie∪Iz；U为车站集合；B 为快运箱集合。

2） 索引。 i,j 为列车索引，i,j ∈I ；k 为高铁快运专列索引，k ∈Iz；u,v 为车站索引，u,v ∈U 。

3） 参数。 Tb为快运柜b 运达对应装车站的时间，b ∈B ；Ob和Db分别为快运箱b 对应的装车站和目的站，b ∈B ；Siu为列车i 在u 站是否停站，若停站，=1，否则，=0，i ∈I ，u ∈U ；Ci为列车i 的装运能力；TRiu为列车i 从u 站到u + 1 站的纯运行时间，i ∈I ，u ∈U{n}；分别为高铁快运专列k 的最小和最大停站时间，k ∈Iz；TEk和TLk分别为高铁快运专列k 在始发站的最早及最晚出发时间，k ∈Iz；Hd和Ha分别为列车最小出发和最小到达安全间隔；ℜ 表示高铁快运专列的启停附加时分；M 为充分大地正整数。

4） 变量。 tdiu为列车i 在u 站的出发时刻；taui为列车i 在u 站的到达时刻；tsiu为列车i 在u 站的停站时间。对于新增快运专列i ∈Iz，列车到达出发时刻和停站时间为本文的决策变量；当列车i 为图定列车（i ∈Ie）时，则为参数；xbi为快运箱配装决策变量，=1，快运箱b 配装在列车i 上，=0，否则；yui,j为列车在车站的出发顺序，=1，表示列车i 在u 站先于列车j 出发，=0，否则。

2 模型建立

基于分阶段优化的特点，可根据上一阶段内的需求（包括滞留需求）计算确定规划阶段内是否需要增开快运专列及增开快运专列的数量，具体的确定方法本文不再赘述。当无新增快运专列时，仅需对快运箱的配装方案优化，即对快运箱配装在哪列图定的列车上进行决策，进而确定规划阶段内列车装卸及滞留的快运箱数量。当需要增开快运专列时，需对新增的快运专列时刻表和快运箱配装方案综合优化。

下面分别建立无新增快运专列条件下的配装方案优化模型（M1）和新增快运专列条件下列车时刻表及配装方案综合优化模型（M2）。首先需要厘清快运箱需求与列车时刻表和配装方案的耦合关系。图3 展示了列车在途中运行、停站以及在各个车站对快运箱的配装过程。为方便说明和模型建立，这里引入关于列车装载状态的3 个辅助变量，分别定义如下。

2.1 快运箱配装方案优化模型（M1）

2.1.1 优化目标

为减少快运箱的运达时间，提高快运箱的运到时效，本文以所有快运箱运达装车站起到运达目的站的总时间最短为优化目标，包括快运箱在对应装车站的等待时间和途中旅行时间，可描述为

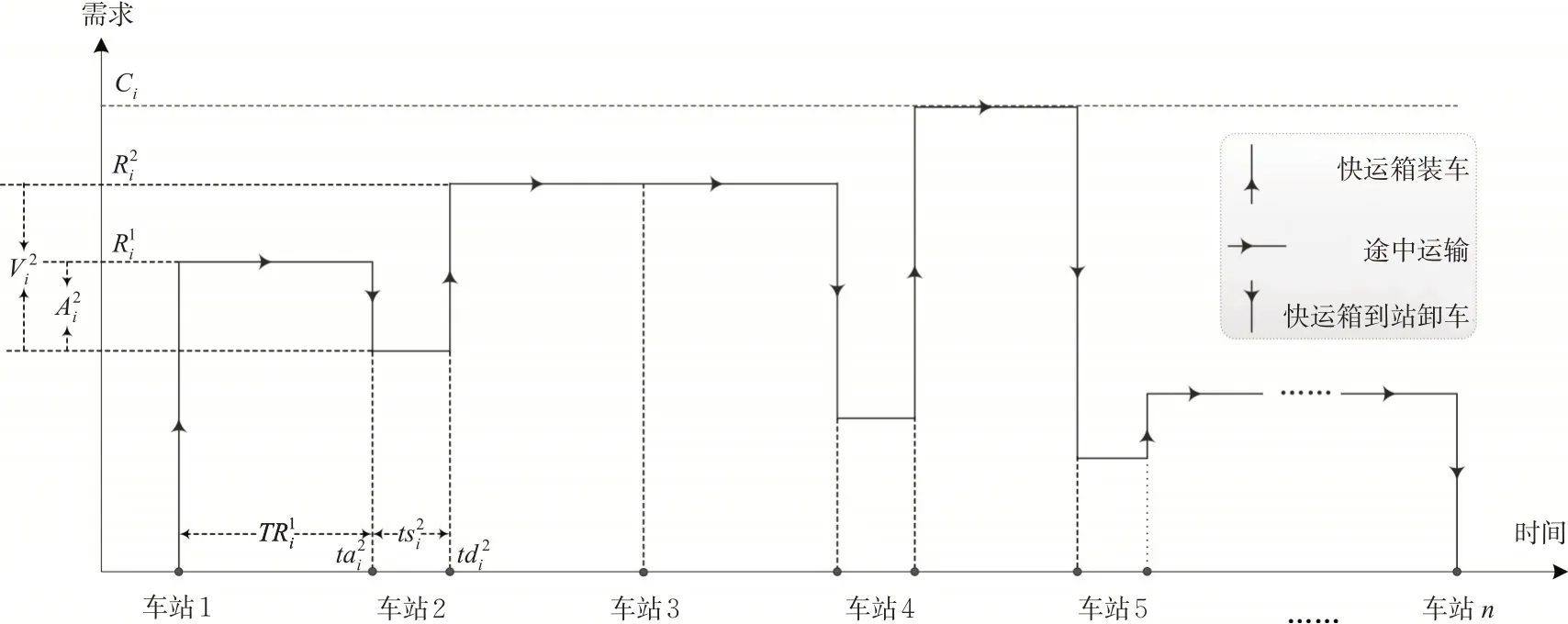
图3 列车时刻表和需求耦合关系Fig. 3 The essential relationship for the train timetable and demand

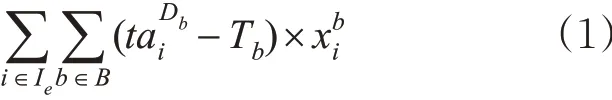
如果仅以此时间为优化目标，可能导致所有快运箱均不能装车，即= 0 ，∀i ∈Ie，b ∈B ，此时目标值为0。为避免这种不合理的情况出现，在优化目标中，为不能在本阶段配装的快运箱一个较大的惩罚，设P 为惩罚因子。则所有快运箱在本阶段不能被配装的惩罚见式（2）。当惩罚因子取足够大的值时，不会对优化结果起决定性的作用。

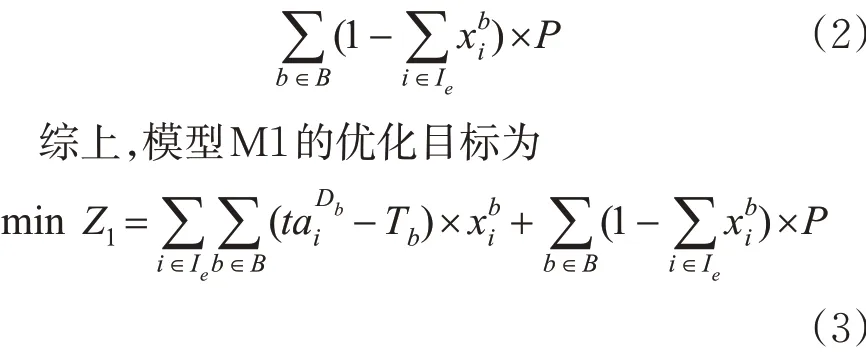
2.1.2 约束条件

1） 列车出发时刻与快运箱配装变量的关系。当列车i 在快运箱b 装车站的出发时间晚于快运箱b 运达装车站的时间Tb，则快运箱b 既可以配装在列车i 上，也可以不配装在列车i 上，即为0或者为1；当列车i 在快运箱b 装车站的出发时间tdObi 早于快运箱b 运达装车站的时间Tb时，则快运箱b 不能配装在列车i 上，即= 0 。由于本文考虑的快运箱均早于列车出发时刻运达装车站，因而，不存在后一种情况。

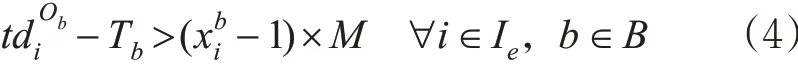
2） 列车停站与快运箱配装变量的关系。当列车i 在快运箱b 的装车站Ob和目的站Db均停站时，则快运箱b 可能配装在列车i 上；否则，快运箱b不能配装在列车i 上。

3） 列车装载状态。由图3 可知，列车i 在u 站装载的快运箱数量为

列车i 到达车站u 卸下的快运箱数量为

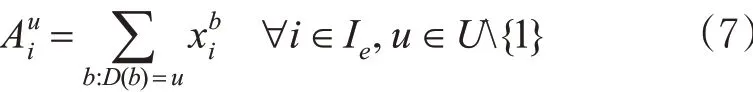
列车i 从u 站出发时车上装载的快运箱数量为

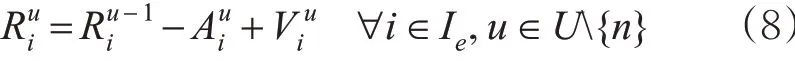
4） 列车装载能力。列车i 从u 站出发时车上装载的快运箱数量不能超过列车的装运能力。即

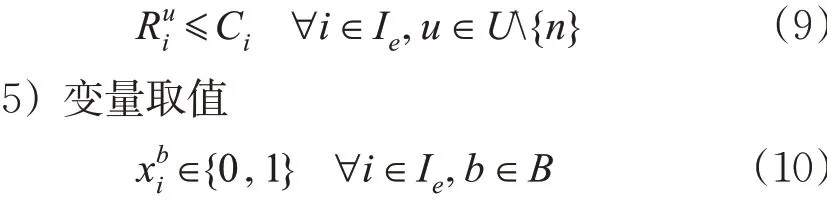
综上，无新增快运专列条件下的配装方案优化模型为

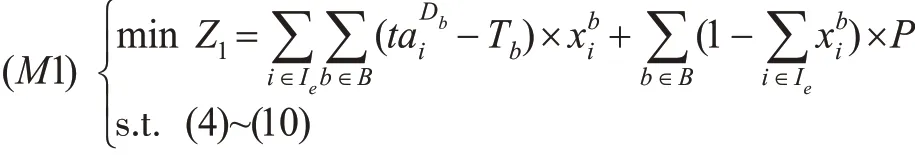
2.2 面向时变需求的快运专列时刻表及配装方案综合优化模型（M2）

当有新增快运列车时，由假设1）可知，新增快运专列的数量和停站方案预先确定。如前文所言，列车时刻表问题和配装方案问题关系密切，需要对新增快运专列的时刻表和配装方案综合优化，即综合确定新增快运专列在车站的到发及停站时间和快运箱的配装方案。值得说明的是，为简化问题，传统的对运输组织中2 个相互影响的问题一般采用“两阶段”的优化方法[15-16]，与综合优化相比，这种两阶段优化方法难以保证解的质量。后文将对本文采用的综合优化方法和两阶段优化方法进行比较。

2.2.1 目标函数

新增快运专列条件下，仍以所有快运箱运达装车站起到运达目的站的总时间最短为优化目标。显然，目标函数（11）是非线性的，后文将对该目标函数进行线性化处理。

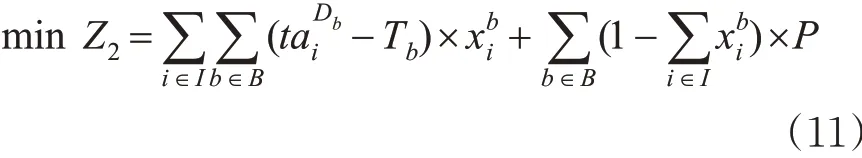
2.2.2 约束条件

1） 快运箱装配。快运箱的配装约束在形式上同模型M1的约束（4）～（9），只是这些约束在这里是对于阶段内所有列车（∀i ∈I ），包括新增的快运专列。

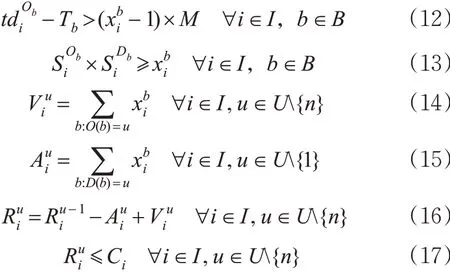
2） 新增快运专列运行。对于新增快运专列k ，给定在始发站的出发时间窗[TEk,TLk] 是大多研究列车时刻表文献的普遍方法。为保证新增快运专列时刻表的灵活性，本文取TEk为研究阶段的开始时刻，TLk为研究阶段的结束时刻。新增列车的出发时刻约束、停站时间约束和运行约束分别为式（18）～（20）。

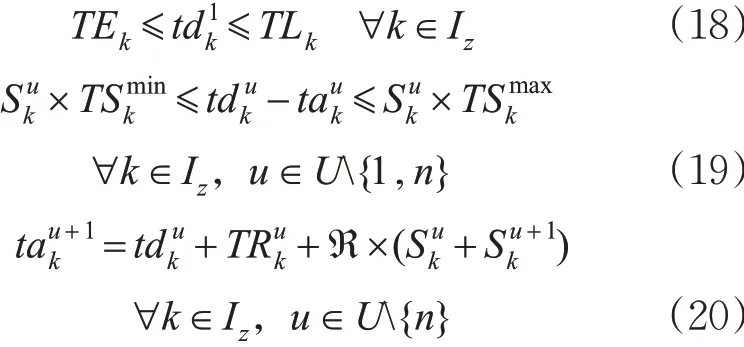
3） 安全间隔及越行。由于新增的快运专列可能被图定的高速列车越行，因而，引入了关于任意2列列车在车站出发的顺序变量，统一刻画列车之间的到发安全间隔约束和越行约束。当列车i 先于列车j 在u 站出发时，即= 1 ，此时后行列车j 与前行列车i 在u 和u + 1站分别满足最小出发和到达安全间隔；反之，不等式（21）～（22）恒成立。

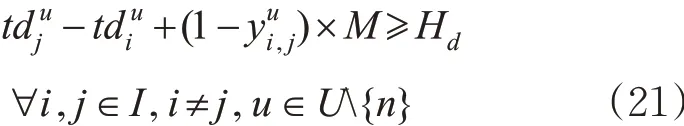
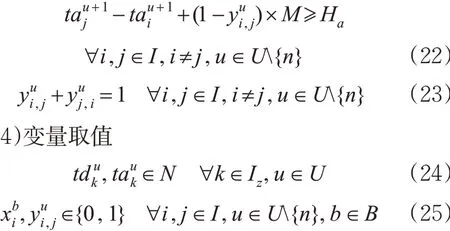
综上，面向时变需求的高铁快运专列时刻表及配装方案综合优化模型为

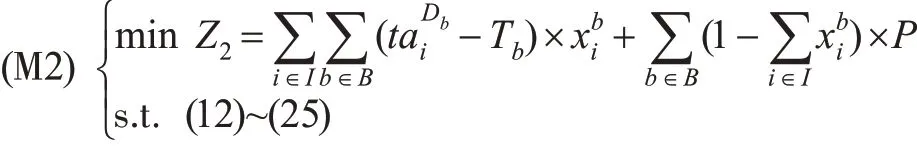
2.3 模型分析与求解方法

本质上，配装方案优化是非标准指派问题，可以利用经典的匈牙利算法对0-1 整数规划模型M1 精确求解[17]。模型M2 为带有线性约束的非线性混合整数规划模型，对于此类问题，可以对模型的非线性目标进行线性化处理[18]。具体地，引入新的整数变量，令

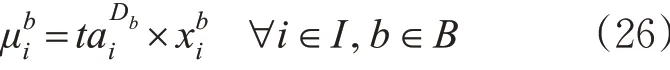
该非线性等式可以利用1 组线性约束等价代替，即

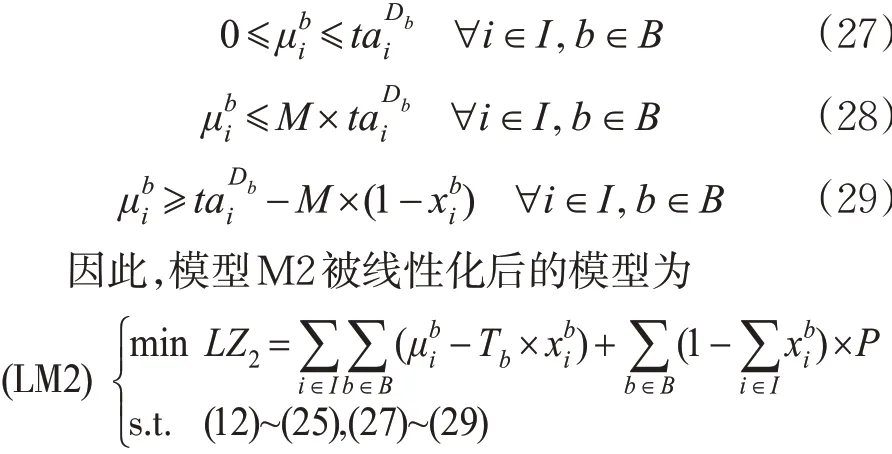
线性化后的模型LM2 可以利用常用的分解算法（如拉格朗日松弛算法、Benders 分解算法、ADMM方法等）将快运专列时刻表及配装方案综合优化问题分解为分别求解列车时刻表和配装方案的子问题，然后单独求解子问题，以获得最优解或者近似解[19-21]。

见表1，模型M1的复杂度主要取决于新增快运专列和快运箱的数量。模型LM2 的复杂度主要由列车数量、车站数量及快运箱需求数量决定。根据本文分阶段优化的特点，在研究阶段内，新增列车的数量一般较少，模型中变量的组合特性不明显，从而无需设计复杂的求解算法，可以直接利用通用优化求解器直接对模型求解，在较少的时间可以获得最优解或近似最优解。基于此，本文对模型M1和LM2利用通用优化软件GAMS的CPLEX求解器求解。

表1 模型约束数量Tab. 1 The number of constraints

3 实例分析

以宁杭高铁线路为例，选择全天运营时段内的第2个阶段（09:00—12:00）为研究对象。图定列车时刻表来源于列车运行图编制系统（实验版）的2018年第一季度数据，该数据可能与实际存在偏差，但并不影响算例分析说明。为方便描述，对线路上的车站依次编号为1～11。限于篇幅，本文所使用的图定列车时刻表和快运箱需求数据以及源代码全部上传至https://github.com/ruhugao/paper-resource-code。

3.1 无新增快运专列条件下配装方案分析

当线路上无新增快运专列时，在图定列车时刻表给定的基础上，仅需要将运达各站的快运箱配装到图定的列车上，直接利用CPLEX 求解器求解模型M1即可得到最优的快运箱配装方案，快运箱不能被配装的惩罚值设为P =10 000，给定运达线路上各车站的快运箱数量为1 000个。程序运行时间为0.01 s，目标值为2.375 732×106。限于篇幅，这里不再展示具体的快运箱配装方案。最后滞留的快运箱的数量为209，被配装的快运箱总的运达为2.373 7×106-209×10 000=285 732。各车站快运箱被服务及滞留的数量见图4，运达车站1～6和10的快运箱全部被配装，由于图定列车在第7站均不停车，导致该车站的快运箱全部滞留。由于列车能力的限制，车站8和车站9部分快运箱没能被配装。以第8 站为例，各个列车对该车站运达的快运箱配装及滞留情况见图5。

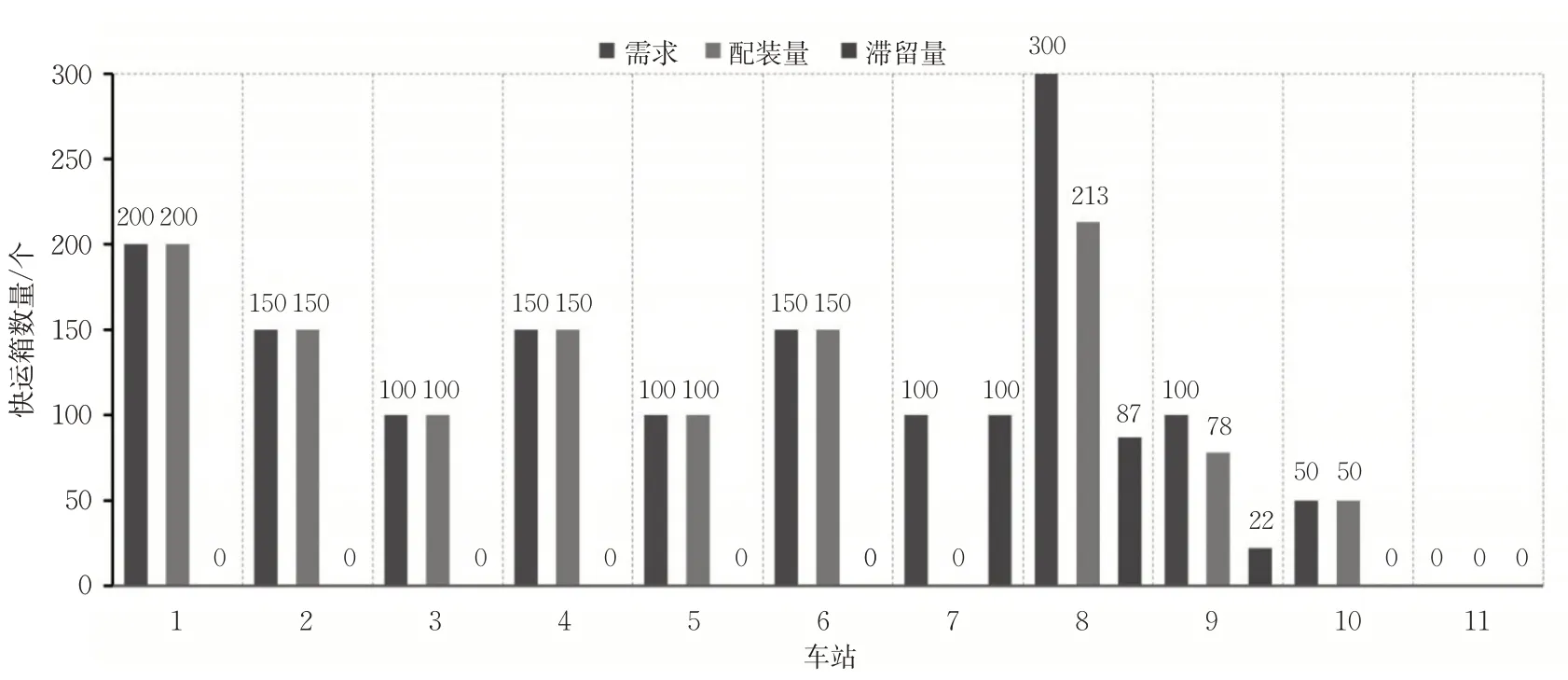
图4 各车站快运箱的配装及滞留数量Fig. 4 The loading and remaining amounts of special delivery boxes at each station

3.2 新增快运专列时刻表和配装方案分析

在新增快运专列条件下，传统的对列车时刻表和配装方案的优化方法是两阶段法，即先对列车时刻表优化，然后在列车时刻表的基础上，再优化配装方案。值得说明的是，这里“两阶段”优化方法与前文“分阶段”优化思路的含义不同，前者表示列车时刻表与配装方案分2 个阶段优化，后者表示按“阶段计划”的优化思路。为便于和本文提出的综合同优化方法比较，将传统的两阶段法模型定义为SM2。模型SM2 的列车时刻表优化阶段一般以列车旅行时间最短为优化目标，配装方案优化同样以快运箱运达时间最少为优化目标。模型SM2 为

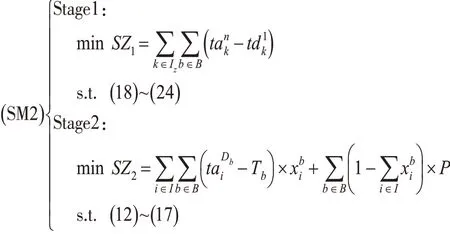
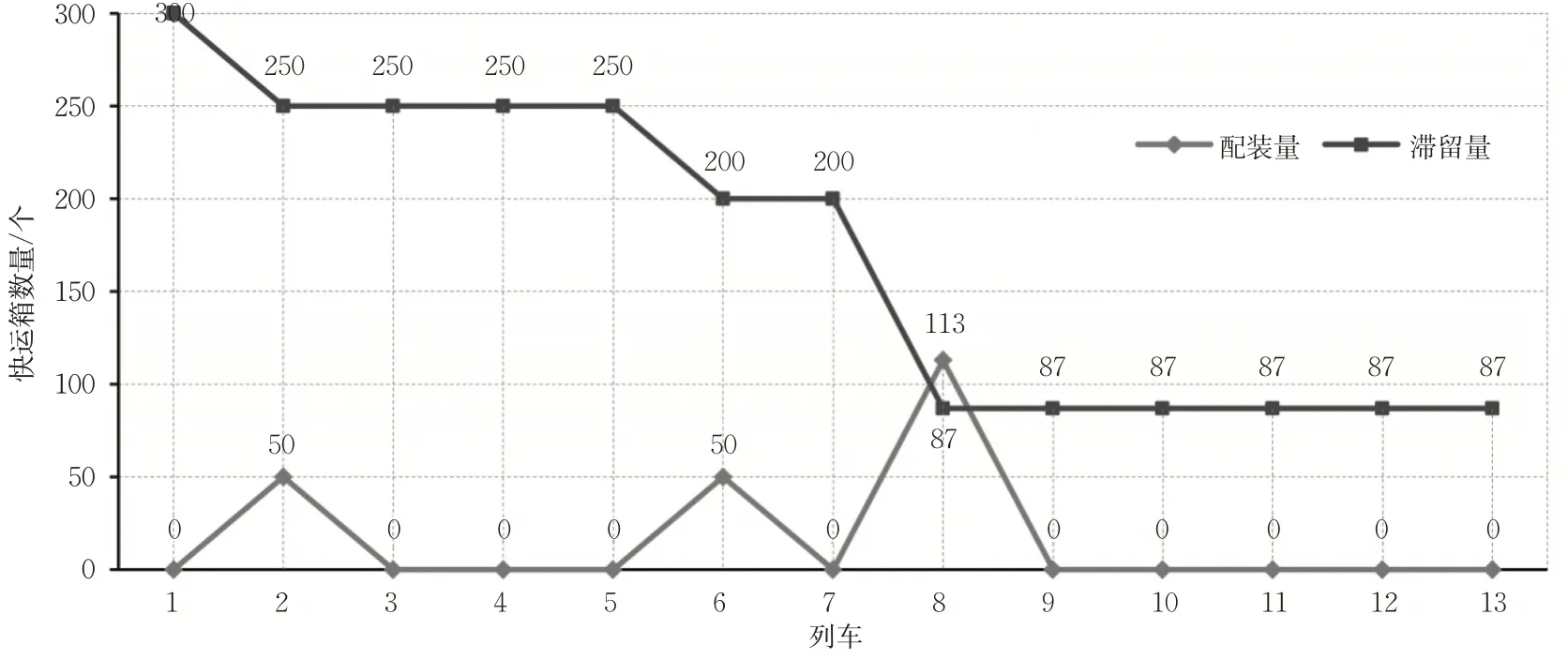
图5 各列车在第8站的配装量及发车后滞留数量Fig. 5 The loading and remaining amounts of special delivery boxes at the 8-th station for each train

宁杭高铁列车最小出发和最小到达安全间隔均为4 min，给定运达线路上各车站的快运箱数量为5 400 个，假定新增列车3 列，运载能力均设为400，假定新增列车停站方案为站站停模式，最小停站时间为2 min，最大停站时间为15 min。同样利用CPLEX 求解器对两阶段优化模型LM2 和综合优化模型SM2 求解，结果见表2。新增快运专列后，列车运行图见图6。

表2 求解结果比较Tab. 2 The comparison of computing results for model SM2 and LM2

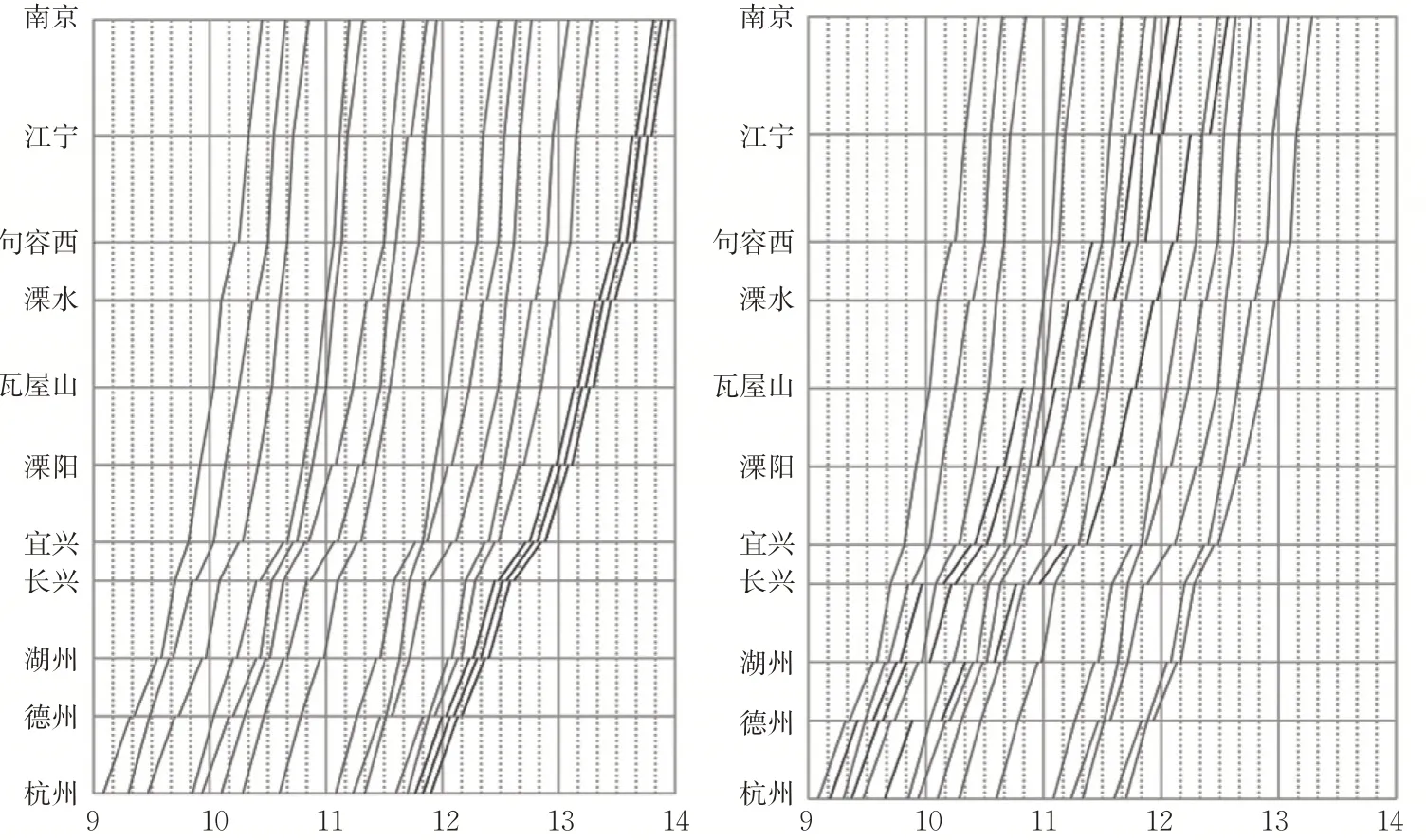
图6 2种方法优化的列车运行图Fig. 6 The optimized train timetable of two different optimizing methods

从结果中可以看出，两阶段优化方法的计算时间较短，并且gap 值为0，但目标值较大。综合优化方法在可接受的计算时间范围内求得近似最优解，目标值比两阶段法的目标更优。有趣的是，2种优化方法求得的快运箱滞留数量相同，这意味着总的被配装的快运箱数量也相同，但2种方法快运箱的运达时间却相差较大。从列车运行图中可以看出，两阶段法在求解列车时刻表时没有考虑需求，求解得到的新增列车运行线均位于本阶段的末端，导致配装方案中快运箱运达时间较大。而综合优化方法，在优化新增列车时刻表时，以需求为导向，使得快运箱的运达时间大大较少，与两阶段优化方法相比，总的快运100%= 17.80%。

4 结束语

以高铁快运列车时刻表为研究对象，以快运箱运达时间最少为优化目标，以高铁快运时变需求为导向，构建了无新增快运专列条件下的快运箱配装方案优化模型（M1）和新增快运专列时刻表和配装方案综合优化模型（M2）。对带有线性约束的非线性混合整数规划模型M2 进行了线性化处理，通过对模型的复杂度分析，本文利用高效的通用求解软件GAMS的CPLEX求解器对模型精确求解。通过实例验证表明，在时变需求驱动下的列车时刻表和配装方案综合优化方法与传统的两阶段法优化方法相比，更能缩短快运需求的运达时间，提高快运需求运到时效性。未来有必要对新增列车数量不确定情况下的列车时刻表进行优化，提出相应的优化算法，使得优化的列车时刻表更加贴合实际，实现高铁快运的动态调度。同时，针对高铁网络的快运列车时刻表优化也是一个有趣的研究方向。