基于路网空间拓扑结构的交通流数据填补模型研究*

孙江涛 钟 鸣▲ 马晓凤 刘少博

（1. 武汉理工大学智能交通系统研究中心 武汉430063；2. 武汉理工大学国家水运安全工程技术研究中心 武汉430063）

0 引 言

随着城市化进程的加快，城市交通基础设施建设速度也是逐年增加的，由此带来的是汽车保有量的迅速增加，2018 年我国新注册登记机动车3 172万辆，机动车保有量已达3.27 亿辆，其中汽车2.4 亿辆，小型载客汽车首次突破2亿辆；机动车驾驶人达4.09亿人，其中汽车驾驶人为3.69亿。同期，武汉市机动车保有量超过324 万辆，同比增长12.6%。随着机动车保有量的增加，带来的是交通问题的增加，及时和正确掌握交通状况对于交通决策起着相当重要的作用。

针对出现的种种交通状况，决策者需要掌握精确的实时交通流数据，但由于实际情况下交通检测器自身故障、损坏，以及传输的种种问题，交通流数据存在大量的丢失。以往存在的数据丢失情况，研究者通常利用自身检测器的历史数据进行丢失数据填补[1]。

关于数据补齐，美国州政府公路交通官员联合会[2](AASHTO)提交的指南中定义了2 条重要的原则:①基础数据完整性原则，采集到的原始数据保存时不应做修改或调整，以保证足够的未经修改过的基础数据用于数据补齐，且补齐数据与原数据应分别存储；②补齐流程的真实性原则，通过文档记载补齐的整个操作流程，有助于增强补齐工作的透明度以便于取舍。

文献研究发现大量关于交通流数据丢失的研究[3-4]，但同时发现对交通流数据填补方面的研究相对很少。20世纪90年代美国、加拿大和欧洲[5-6]等国家多采用历史数据构建补齐模型；姜桂艳等[7-8]采用前1 d的历史数据、前后邻接时段的数据、前几个时段数据以及相邻路段数据实现丢失数据的补齐；Southworth等[9]构建了RTMAS系统，该系统能够应用于城市紧急疏散中。系统中的AUTOBOX 模块根据历史交通流数据进行自回归平均来预测出每个小时的交通流量，从而填补预测出丢失的交通流数据[10]。同样Zhong等[11]采用因子模型、自回归综合移动平均（ARIMA）模型、遗传设计回归模型和神经网络模型对缺失值进行估计。

少量关于交通流数据填补的研究往往是对时间序列下的数据进行小片段预测[12-13]，无法全面考虑数据完整性。Gold等[14]认为应该首先尽可能全面的了解丢失的产生过程，然后根据丢失的性质采取相应的方法补齐，他们采用的补齐方法有Factor Up 插值、线性插值、基于期望最大化估计的多项式回归及核回归等，采用的算法能够实现5 min 以内的丢失数据的补齐，但不能解决更大间隔的数据丢失问题；Sun 等[15-16]利用非参数回归中的局部线性回归模型进行丢失数据的补齐。韩卫国等[17]利用常见的插补法，比较分析平均值法、最大期望法和数据增量法三者之间的优缺点，并根据比较分析结果展望未来交通流数据填补的研究方向。Martin等[18]根据丢失数据的产生间隔不同，开发了不同的补齐方法，主要包括因子法、时间序列法、邻近检测器(时间、空间)数据预测方法等。

从以上文献中可以看出，以往的研究往往都是基于本地历史数据对交通流数据进行填补，但是这些方法在本地历史数据缺失的情况下无法应用。因此，本研究针对传统数据清洗中丢失数据填补模型存在的不足，在数据填补算法中考虑路网的空间拓扑结构。模型算法充分考虑检测器数据的时间和空间关系，能够提高交通流数据填补的速度和精度。

1 基于空间拓扑结构的交通流数据填补模型构建

武汉市交通检测器的在线率常年稳定在20%～30%，交通检测器数据存在大量丢失，对于交通检测器数据的丢失情况，需要对其进行数据补齐，但是初步的数据分析表明，大量的交通检测器的历史数据存在大量缺失，历史数据量并不能完成检测器丢失数据的填补，本研究考虑采用交通网络的空间拓扑结构，利用时空关系进行丢失数据的填补，具体算法的流程见图1。

对于交通检测器数据缺失，根据交通检测器编号找到该检测器的数据表，查找该检测器历史周中相同工作日中是否有足够的数据进行丢失数据填补，如果数据足够，则利用该检测器的历史数据进行填补，填补算法为检测器历史数据取平均值作为丢失数据；如果检测器历史数据不足，下一步链接交通检测器数据表，找到缺失路段的编号，然后判断该路段是否含有其他类型的交通检测器。

1） 如果该路段含有其他类型的交通检测器，继续检查该检测器当前时刻是否含有数据，如果含有数据，则根据不同车道之间的权重（后续将介绍权重计算方法）进行数据填补；若该检测器没有数据按该路段没有检测器处理。

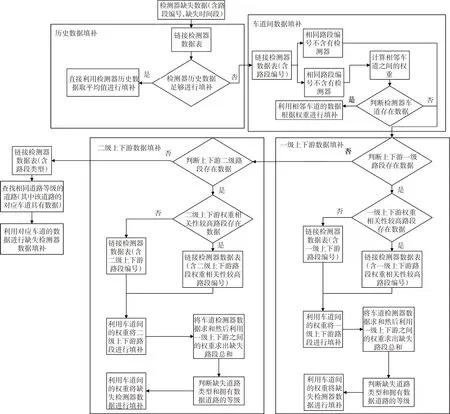
图1 基于拓扑结构的交通流数据填补流程图Fig. 1 Improved imputation methods flowchart for traffic flow data based on spatial topology

2） 若没有相同类型的检测器，则根据上下游数据进行填补，具体如下:链接到ArcGIS 路网信息表，根据丢失路段的拓扑结构确定上下游的路段编号。

根据丢失检测器的路段编号，找到该编号对应的From_node 与To_node，根据From_node 来找到上游路段编号中对应To_node 的路段，同理可以找出下游路段的路段编号。根据上下游路段编号判断一级上下游权重相关性较高的路段车道是否含有交通检测器数据，如果一级上下游权重相关性较高（后续介绍权重计算方法）的路段含有交通检测器的数据，则利用上述所说的车道间权重将一级上下游所有车道的数据全部补齐，再根据车道之间的权重关系将交通检测器的丢失数据进行补齐；如果一级上下游权重相关性较高的路段中交通检测器数据没有数据，继续判断一级上下游权重相关性次之的上下游道路，若找到交通检测器含有数据则填补方法如权重相关性较高的道路填补方法。

在上下游一级道路未找到交通检测器含有数据，则考虑上下游二级道路，如果上下游二级道路中交通检测器含有数据，则根据上下游一级道路处理方法相同进行丢失检测器填补。

在检测器路段一二级上下游均未能找到相应的检测器数据，则继续链接到交通检测器数据表（含有道路类型），在该表中找到与交通检测器数据丢失路段相同的道路类型，在交通检测器数据表中找到与丢失数据路段中相同车道上交通检测器中的数据，将该数据直接应用于丢失数据路段中。

本文构建的交通流数据填补模型在传统交通流数据填补模型的基础上加入空间拓扑结构的填补。模型利用近邻分析模型完成交通检测器的历史数据填补，并在此基础上考虑实际交通网络的空间拓扑结构，构建了基于空间拓扑结果的车道间数据填补模型和上下游空间数据填补模型。相对于传统交通流数据填补模型而言，本文构建的基于空间拓扑结构的交通流数据填补模型能更好地解决实际情况下交通检测器数据丢失严重的情况，并在历史数据填补模型失效的情况下，进一步找寻丢失检测器路段的空间拓扑结构关系，提高数据填补的能力。

2 拓扑关系权重计算

2.1 计算不同车道之间的权重

对于不同道路类型中不同车道之间的权重标定，首先需要构建基于流量数据的不同车道间权重计算的算法，利用编程将算法实现，对挑选出的典型道路数据进行程序处理，得出相应车道间的权重值，最后将权重值存储为静态文件，以便后续对其调用应用到填补算法过程中。

权重算法计算分为工作日和非工作日2 种类型，工作日和非工作日中又分为每个小时不同车道之间的权重。根据道路等级对路网道路进行分类，其中道路等级分为快速路、主干道、次干道和支路，由于在实际情况下不同道路的车道数是不一样的，本研究将所有车道数划分为最内侧车道、中间车道和最外侧车道3类，具体划分原则见表1。

表1 不同车道数分类表Tab. 1 Classification table of different lane numbers

将车道划分完成后，需要计算不同车道之间的权重关系。训练一定量不同道路类型的权重值作为典型道路，具体算法流程为:链接到不同道路类型下交通检测器的数据表，找出工作日不同车道检测器一段时间的数据，然后判断这一段时间中车道的数据量值最小的数据量Xmin，然后其他车道的数据量均取对应这个最小的数据量Xmin，将不同车道的所有数据值进行相加得到不同车道总的交通检测器数据值Sumi，然后将不同车道的数据总和作为不同车道之间的比例系数，也就是不同车道之间的权重。即R1:R2:R3=Sum1:Sum2:Sum3。

对于不同道路等级均要算出不同车道之间在工作日和非工作日每个小时的权重。具体流程图见图2。

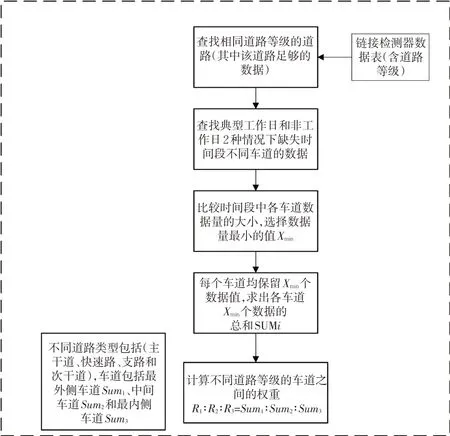
图2 车道间权重计算流程图Fig. 2 Flow chart of calculating the weight between lanes

2.2 计算上下游路段的权重

本文构建基于流量数据的路网上下游权重计算的算法，算法将标定上游一级各路段、下游一级各路段、上游二级各路段、下游二级各路段的流量与目标路段流量之间的关系，在后续模型参数选择时可以调用计算的系数进行模型计算。

基于流量数据的路网上下游权重计算的算法是基于道路网的拓扑结构计算，标定的路段基本结构见图3，其中Q0为目标路段，QlU为一级上/下游路段，QlUi为二级上/下游路段。

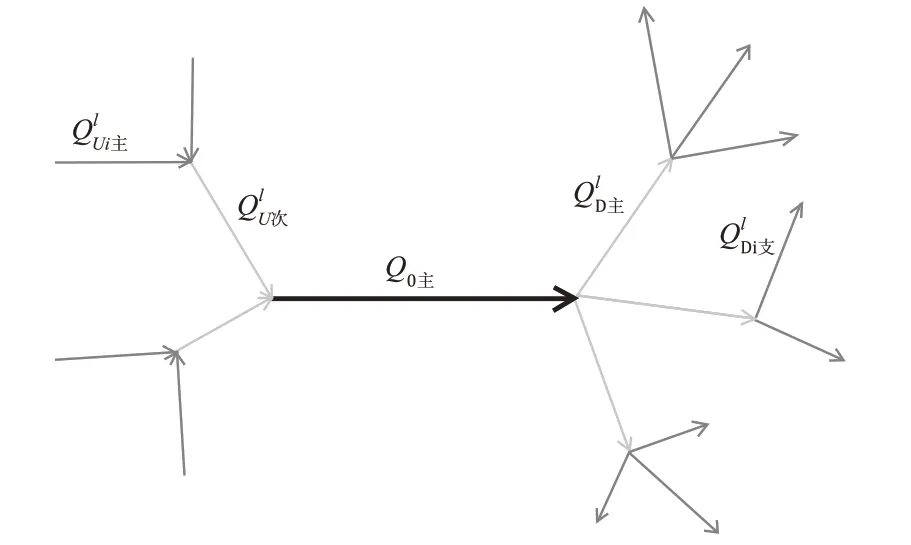
图3 道路基本拓扑结构示意图Fig. 3 The spatial topology of road network

其中标定需要研究的路段流量为Q0；道路的上下游次数为l，当l=1时为一级上下游，l=2时为二级上下游；上游标识符为U，下游标识符为D；一级路段类型为i，i的道路类型分为快速路、主干路、次干路、支路4 种；二级路段类型为j，j 的道路类型同样分为快速路、主干路、次干路、支路4种；上游一级路段流量，下游一级路段流量，上游二级路段流量，下游二级路段流量。

对上下游路段间流量关系采用一元线性回归来描述，对二者构建回归函数公式y = a + bx ，y为目标路段流量值，x 为目标路段的影响范围内上/下游路段流量值。在本研究中，需要先标定一元线性回归函数的参数值。标定通过获取工作日及非工作日的流量数据，对相应时段内的目标路段和上/下游路段的流量采用一元线性回归函数模型进行相关关系分析。对此参数值的标定采用最小二乘解的方法。利用流量数据计算参数的公式见式（1）。

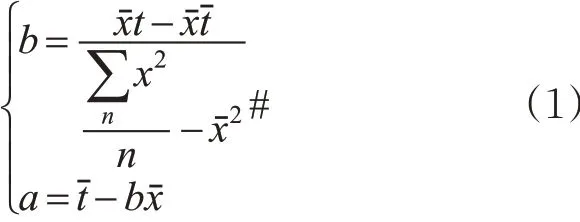
根据上述一元线性回归函数，确定考虑了道路等级的路网拓扑结构回归函数参数符号。在路段权重标定的过程中，目标路段与一级上游路段间的权重系数为，与一级下游路段间的权重系数为，与二级上游路段间的权重系数为、，与二级下游路段间的权重系数为。本级路段流量均值上游二级路段流量均值，下游二级路段流量均值。以一级上游为例，权重参数值的计算公式见式（2）。

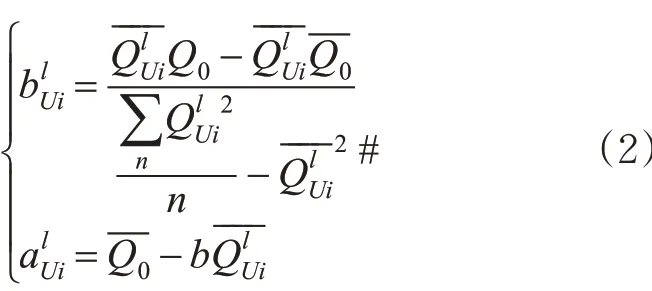
一二级上/下游路段与目标路段间权重的标定流程见图4。

在实际的空间填补模型使用过程中，根据某一上/下游流量值和标定的参数计算目标路段的流量值。具体的表达式见式（3）。

3 实例分析

武汉市智慧决策系统是由武汉理工大学智能交通中心综合研究所与武汉市公安局交通管理局联合开发的武汉市交通管理决策系统，该系统对武汉市地磁检测器、卡口电警、线圈检测器共计5 869 个点位、20 713 个检测器进行监测。通过系统的地图及检测器的空间化信息能够确定检测器、路段的具体位置及空间关系。该系统以1 min的时间间隔将全路网的数据将检测器接入到系统中。系统功能主要包括检测器的数据采集质量分析、检测器数据清洗及填补、检测器数据融合、短时交通流量预测及交叉口评估等。

由于不同功能的道路具有不同的交通流特性，因此考虑根据道路的功能对相应道路下的link进行道路功能组分类。按照现有的道路等级，对市域内的link路段进行道路组的划分，分别分为高速路、快速路、主干道、次干道、支路和辅路6 个道路功能组。构建基于空间拓扑结构的交通流数据填补模型。在使用该模型前，需要输入各个link 的历史数据，通过相应的预测模型离线参数学习标定后，再上线使用。

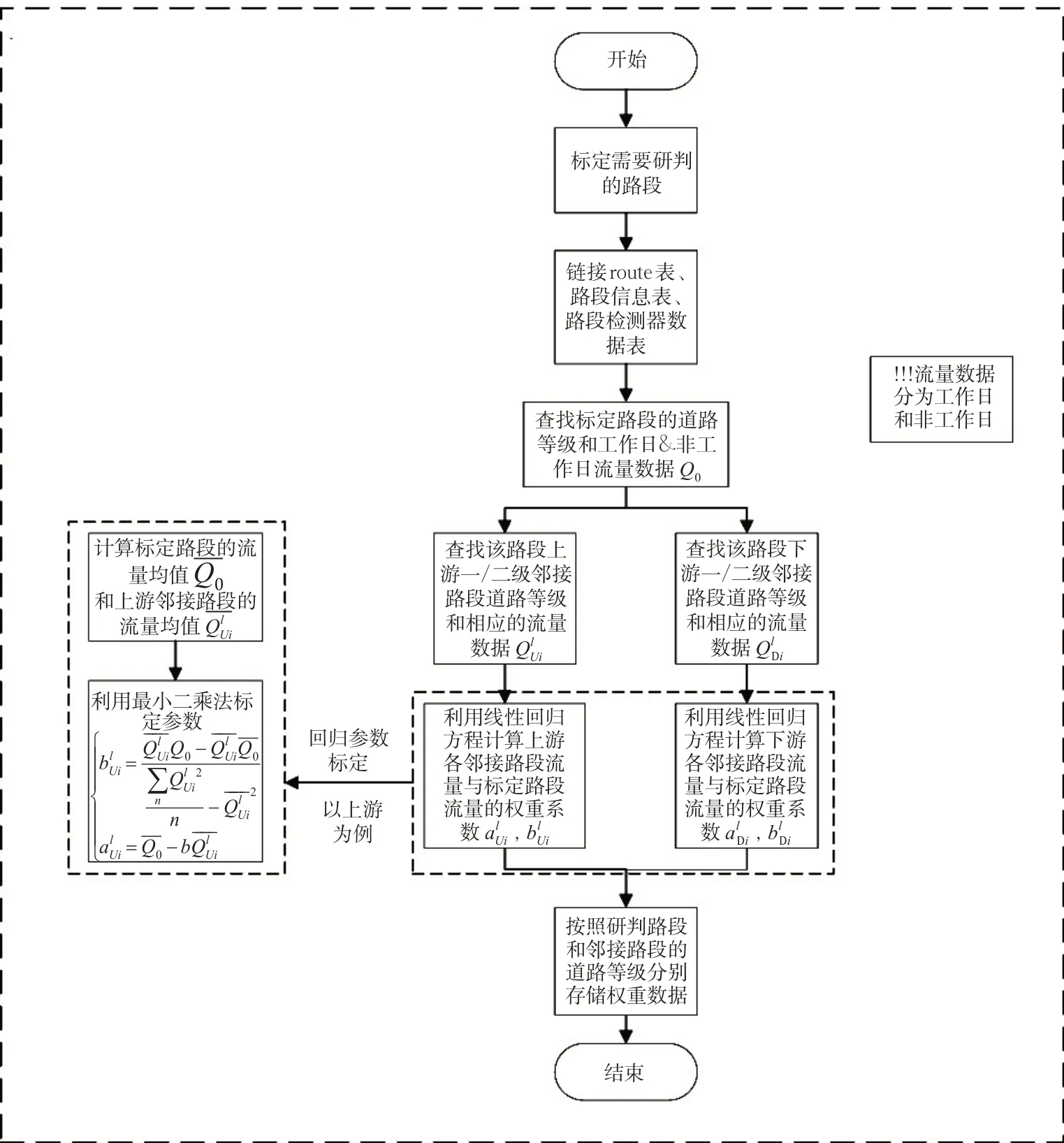
图4 一/二级上/下游路段与目标路段间权重的标定流程图Fig. 4 The calibration flow chart of the weight between the first and second upstream/downstream sections and the target section

基于空间拓扑结构的交通流数据填补模型针对交通流检测器数据丢失严重情况，采用检测器的自身数据无法完全填补，本文构建基于空间拓扑结构的交通流数据填补模型。利用武汉市的交通检测器数据进行模型验证，由于武汉市实际道路检测器数量过于庞大且模型精度测试相对繁琐，因此本论文验证数据采用的是武汉市1条路段上的地磁检测器数据，其中路段的编号为1 015，地磁检测器的编号为A08456和A05638。选取时候的原则是确保该检测器的数据完整且路段上下游含有数据的交通检测器。

验证时假设检测器的数据缺失，利用模型方法将缺失的数据进行填补，得到填补完成后的检测器数据和检测器原始数据进行对比分析，对比得到模型不同阶段的填补误差，采用平均绝对百分比误差（MAPE）计算，具体的计算公式见式（4）。

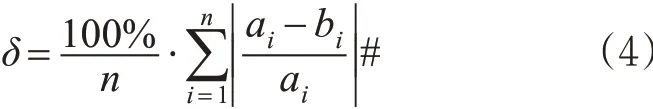
式中:δ 为模型误差；a为检测器自己原始数据；b为模型填补之后的数据；n为测试数据的个数。

测试采用实际的2 个地磁检测器的数据进行，数据时间跨度为1 d 24 h，时间粒度是1 min。根据检测器时间跨度和时间粒度可得实验样本数据量为1 440。实验分别验证不同填补方案对应的填补误差，得到表2。

从表2 可看到，基于空间拓扑结构的交通数据填补模型的2个检测器精度测试的平均相对误差分别为52.88%和51.93%。由于模型车道间和上下游的空间拓扑结构对丢失数据进行填补，上下游和车道的空间关系均对交通流的影响较大，因此数据误差相对较大。但相对于传统交通流数据填补模型，本文提出的模型能解决传统模型不能填补的问题，在现实应用中具有较大的实用性。

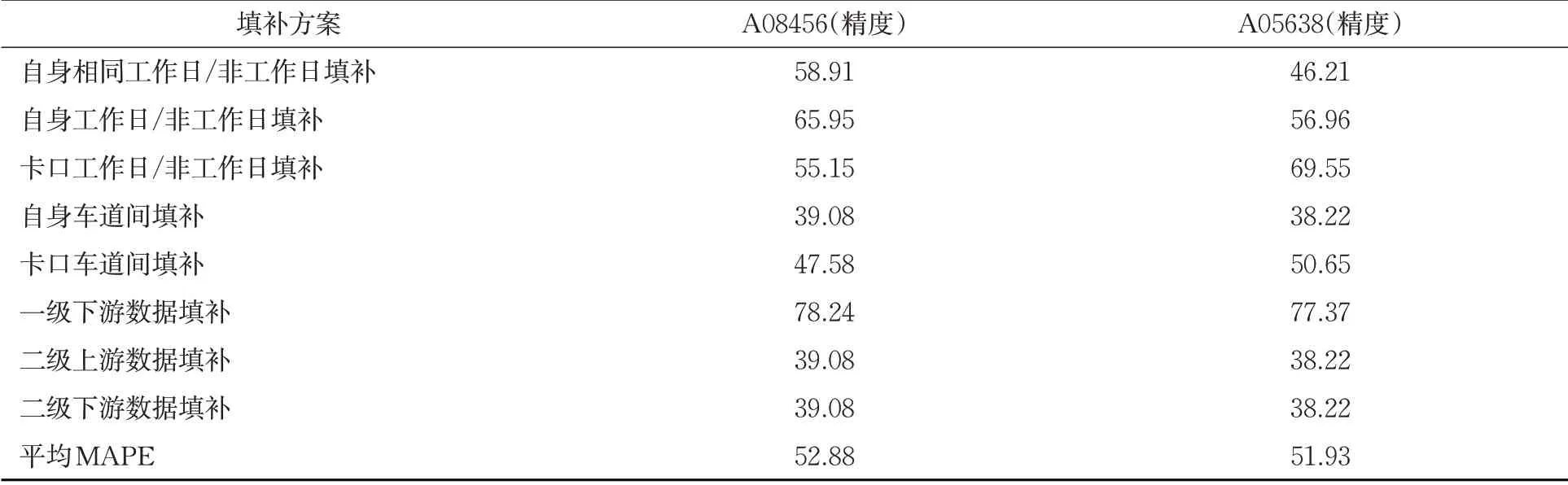
表2 不同填补方案实验误差结果Tab. 2 Experimental APE of different filling model 单位:%

4 结束语

交通流数据作为城市交通规划和管理的基础来源，数据质量的好坏直接影响到实际的路况分析和交通决策，但由于交通检测器数据在实际情况下往往出现大量的丢失，因此对交通流数据填补变得尤为重要。通过阅读交通流数据清洗中关于丢失数据填补的研究发现，现有的研究大量致力于通过自身交通检测器数据进行填补，通过自身历史数据进行平均或者预测等方法将缺失数据填补完成。基于研究现状，本文通过构建基于空间拓扑结构的交通流数据填补模型，研究通过计算不同拓扑结构下的权重关系，计算典型情况下的权重数值，应用于交通流数据填补，模型打破以往研究的瓶颈，增加其他类型检测器和考虑空间拓扑结构关系，最后通过武汉市实际的交通检测器进行模型验证，实验结果表明模型应用性较强，由于检测器数据丢失情况严重，模型在2 个检测器上的平均相对误差为52.88% 和51.93%。虽然在精度上还需要进一步提高，但是能够在大范围内为交通流检测器填补丢失数据，为智慧交通决策提供数据支撑。