考虑土地利用的单交叉口信号配时方法

吴 键 郭建华

（东南大学智能运输系统研究中心 南京210018）

0 引 言

城市交通拥堵问题是城市发展的重要障碍。城市道路网络中的节点是交叉口，承载交通流的汇集与消散，由此可见，交叉口是城市交通控制的重要节点。

单交叉口信号配时研究很早就得到了国内外学者的关注。从20世纪40～50年代开始，交叉口信号配时成为交通工程工作者的重点研究问题［1］。实际上，目前单交叉口信号配时的研究方法绝大多数都是基于延误理论，通常的延误指的是由于交通摩阻与交通管制而引起的行驶时间的损失，单位通常为s或者min［2］。在延误理论的基础上，Clayton 提出了基础交叉口延误模型［3］。Webster 围绕单点交通信号配时进行了研究［4-5］并提出了信号交叉口延误计算模型［6］。Akcelik［7］提出“停车补偿系数”方法，将车辆平均延误和停车次数最小作为多个优化目标的配时方法。美国《道路通行能力手册》（简称HCM）在1985 版本［8］和2000 版本［9-11］中在交叉口延误计算加入了随机附加延误。日本的《平面路口的规划与设计》一书中，用参数修正饱和流率和交叉口形状等，以实现配时参数的精确性［12］。在国内，任福田［13］在延误模型中加入了车道修正因素。杨晓光等［14］提出了不同车道功能组合、不同车种构成、不同排队次序条件下的非饱和状态车辆延误模拟算法。曹成涛等［15］将交叉口停车次数、通行能力作为性能指标，建立多目标信号配时模型，并通过遗传算法进行求解。Kesur［16］建立了以停车次数、延误最小为优化目标的信号配时模型，并对2个参数进行分析，结果表明，延误随着停车次数的减少而增加。Yuan等［17］建立了以停车次数、延误和排队长度最小化为优化目标的信号配时模型，结果表明，该优化模型提高了交叉口的通行效率。于杰［18］提出了基于人均延误最小策略的交叉口信号配时模型，以实现公交优先的改进Webster 信号配时方法。罗小芹［19］提出了以单点优化方法以及感应控制原理为基础的面向混合交通的感应式交通信号控制方法。前述交叉口信号配时优化都没有将土地利用以数量化的形式引入配时计算中，忽略了土地利用与交通需求的联系。

不同于信号配时方面丰富的研究，在土地利用与信号配时关系方面，国内外基本上处于空白状态，只有少部分定性的研究考虑了交通需求与土地的关系。诸如Lowry 等［20］的研究，考虑了人口、经济、工业、土地等因素对交通量的影响，其中土地的因素只是定性分析土地开发对交通量的干扰，没有涉及信号配时阶段。当前，土地利用因素实际上是引入到交通量预测，试图以土地利用为因变量，抛开传统的调查交通量，求解交通量生成，但是大都停留在简单分析论述上，没有实质性的量化进展［21］。可见，传统意义上的交叉口信号配时是处于交通规划四阶段法之后，而土地利用一般在四阶段法中进行长期交通需求的预测，很难在交通信号配时层面进行实质性的量化分析。

然而，在当前的交通信号管控过程中，土地利用是影响交叉口状态的必不可少的因素。因此，需要以定量的形式使得土地利用因素变成配时计算流程中的修正系数，以在单交叉口信号管控系统中顺利引入土地利用因素。本文在量化分析土地利用强度、土地利用混合度对交通量影响因素的基础上，借鉴经典的Webster 方法，构建考虑土地利用的单交叉口信号配时方法，通过实例研究，运用仿真分析，验证所提出方法的有效性。

1 考虑土地利用的信号配时方法

本文构建土地利用强度修正系数、土地利用混合度修正系数、土地利用融合修正系数，实现土地利用影响下交通量修正。同时，借鉴经典的Webster模型，计算给定的交通流在不同时段下的信号配时，得到考虑土地利用的单交叉口信号配时方案。方法具体流程见图1。

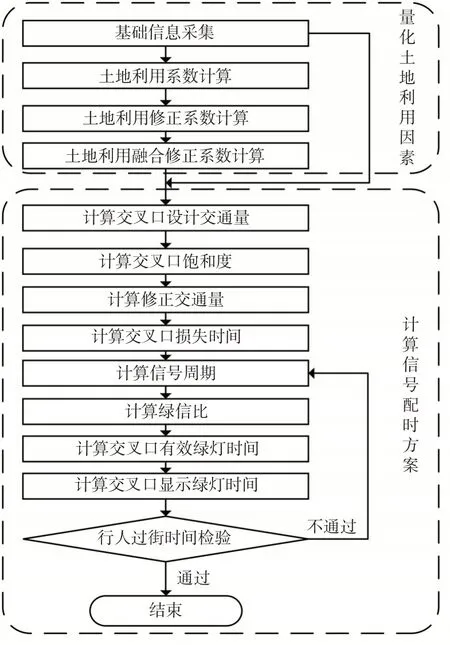
图1 土地利用单点信号配时流程图Fig. 1 Flow chart of land use single point signal timing

为简化土地利用指标的计算，做以下假设:①城市土地规划受到城市规划部门的统一安排布局，土地用地性质的更改一般在短期内不会发生；②各个地块的建筑物容积率是可测的，可以查阅用地规划文件或参考其他同类城市同类建筑物［22］；③可查阅土地规划文件获取混合类型土地面积的划分，如果遇到难以划分的情况，可以采用平均用地面积划分的方法；④只考虑交叉口临近范围内的土地利用影响，不考虑远处其他地块土地利用的叠加影响。

1.1 基础信息采集

为实现基于土地利用的信号配时控制，需要采集基础信息用以服务后续土地利用指标计算和土地利用信号配时，主要包括交叉口信息、土地利用信息和交通量信息3类，见表1。

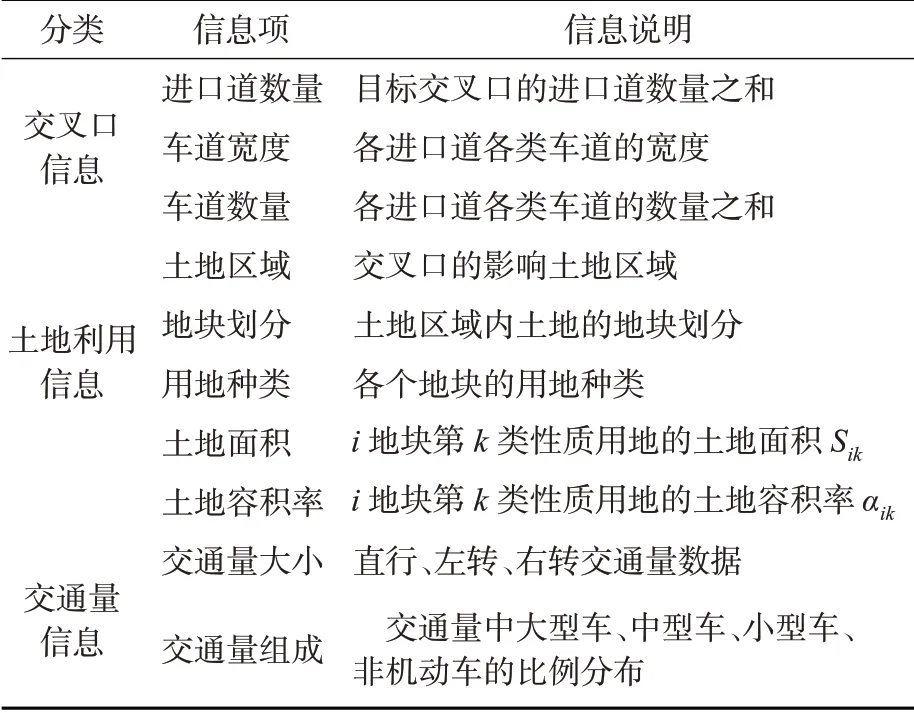
表1 基础信息表Tab. 1 Basic information

1）交叉口信息。交叉口信息主要包括进口道数量、车道宽度、车道数量等。进口道数量用于确定交叉口周边土地分块；车道宽度、车道数量等用于计算交叉口的实际饱和流率和行人最短过街时间检验。

2） 土地利用信息。土地利用信息包括土地区域、地块划分、用地种类、土地面积、土地容积率。

（1）土地区域。以目标交叉口为圆心，以1 000 m为半径画圆，如圆内没有除交叉口进口道以外的干道，则该圆内土地为交叉口的影响土地区域；如圆内有除交叉口进口道以外的干道，则这些干道包围的土地为交叉口的影响土地区域。

（2）地块划分。沿着目标交叉口各个进口道向周围割开，即可将交叉口的影响土地区域割裂为单独的地块。因为地块的划分是按照进口道切割的，故地块的数量和进口道的数量是一致的。由于进入交叉口的车流按照靠右行驶规则，对进口道影响最大的地块是该进口道右侧的地块，且各个地块均可能存在多种性质用地。设i 地块的用地种类数量为Ni。其中i 地块第k 类性质用地的土地面积为Sik，i 地块第k 类性质用地的土地容积率为αik。

（3） 用地种类。按照《城市用地分类与规划建设用地标准》将交叉口的影响土地区域内各个地块中的土地划分为居住用地、商业用地、公共设施用地等多种性质用地。

（4）土地面积。交叉口的影响土地区域内各地块各用地种类的面积，可以测量或者查阅相关规划文件获取。

（5）土地容积率。容积率主要指的是在一个规划小区或者建筑物地上的总建筑面积与其用地面积的比值。交叉口的影响土地区域内各地块各种类土地的容积率可以查阅规划文件获取，或者参考同类城市同类建筑物获取。

3） 交通量信息。交通量信息包括交通量大小、交通量组成。交通量大小、交通量组成用于计算换算后标准车辆的交叉口交通量，为后续修正交通量提供数据基础。

1.2 土地利用系数计算

土地面积、土地容积率作为土地利用影响因素，可以反映交叉口周边土地利用开发的密集程度及多种类土地的混合程度。密集程度和混合程度是干扰进口道交通的2 个土地利用因素，为实现基于土地利用的信号配时，需要将其量化并引入配时计算。本部分对土地利用系数进行计算，包括各地块的土地利用强度系数和土地利用混合度系数。

1） 土地利用强度系数。土地利用强度反映出居民出行的强度特征，土地开发强度越大，其承载的居民出行量也就越大，对交通流的干扰也就越强。现实生活中，城市土地的容积率是土地利用强度的重要表现，容积率与土地利用强度之间呈现正相关关系。由于城市土地规划中地块的开发程度不一致，通常一个地块的建筑面积远大于其用地面积。可取i 地块的上所有建筑面积与土地面积的比值，作为i 地块的土地利用强度系数Mi。

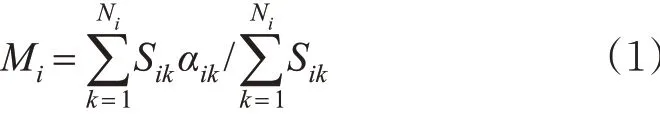
由式（1）可知，Mi是i 地块上的土地容积率的加权平均值。而城市土地容积率由城市规划部门确定，根据我国《建筑工程建筑面积计算规范》可知，一般城市住宅类建筑容积率在0.8～4.5 之间，特殊超高层建筑物容积率可达到5～10之间。

2） 土地利用混合度系数。土地的开发程度不仅仅体现在土地利用强度上，多种类用地混合、多职能用地现象也是土地开发程度的一种表现。土地的混合利用指的是城市规划的某一片区中具有多重性质的土地，这些土地共同组成有机的整体。实际上，越复杂的混合用地情况本身就是一种强不稳定现象，其会对交叉口周边交通流产生干扰。为了量化该指标，类比物理学中的熵（混合度）的概念，提出i地块的土地利用混合度系数Wi。

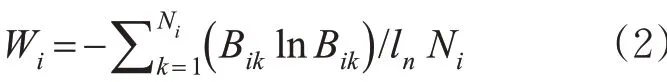
式中:Bik为i 地块中第k 类性质用地的土地面积在整个i 地块中土地面积的占比。

Wi只和i 地块中各类性质用地的土地面积相关，其取值范围为（0，1］。当i 地块中某一性质用地的土地面积占据i 地块的绝大多数比例，其他性质用地的土地面积几乎为0（即混合程度低）时，Wi取值接近0；当i 地块中各性质用地的土地面积比例完全相同（即混合程度高）时，Wi取值为1。Wi取值越大表示i 地块土地利用混合度越高，i 地块中各性质土地混合情况越复杂；Wi取值越小表示i 地块土地利用混合度越低，i 地块中各性质土地混合情况越单一。

1.3 土地利用修正系数计算

本文引入土地利用修正系数用以量化土地利用对交通流的影响，主要有土地利用强度修正系数和土地利用混合度修正系数。考虑分别位处人迹罕至的郊区和繁华的市区的2 个完全相同的交叉口，不同的土地开发情况给进口道交通流带来的干扰是不一致的，因此这2 种情形下的信号配时方案应有所区别。但目前配时方法只和交叉口的观测交通量、车道等因素相关，虽然观测交通量一定程度上间接反映了土地利用的影响，但当前的配时方法却很难直接量化土地利用的干扰，因此，本文引入土地利用修正系数，以数量化的方式描述土地利用对交通流的影响。

1） 土地利用强度修正系数。土地利用强度修正系数是基于土地利用强度系数，对与该地块相对应的交叉口进口道的交通量进行修正的系数。对一般的十字型交叉口而言，共4 个土地利用强度修正系数。根据式（1）可知，Mi是i 地块上的土地容积率的加权平均值，其数值变化区间较大且仅与i 地块相关，而交叉口周边有x 个地块，为了反映i 地块与交叉口周边x 个地块的土地利用强度系数之间的联系与强弱比较，本文以i 地块的土地利用强度系数Mi和x 个地块中最小的土地利用强度系数min(M1,M2,…,Mx) 的比值，作为i地块土地利用强度修正系数ρi。

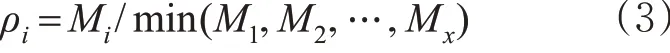
ρi的取值范围为［1，+ ∞）。当Mi是整个交叉口所有地块土地利用强度系数的最小值时，ρi等于1。 i 地块的土地容积率较高，而其他地块的土地容积率均趋于0 时，ρi趋近于正无穷大。事实上在现实生活中，ρi常常在1～2 之间波动。当ρi大于1时，表明i 地块的土地利用强度系数大于整个交叉口所有地块土地利用强度系数中的最低值，即该地块的对应进口道交通流受到土地开发强度的干扰大于整个交叉口的最低值，因此需要对该进口道处的交通量进行放大处理。

2） 土地利用混合度修正系数。土地利用混合度修正系数是基于土地利用混合度系数，对与该地块相对应的交叉口进口道交通量进行修正的系数。对一般的十字型交叉口而言，共4 个土地利用混合度修正系数。根据式（2）可知，土地利用混合度系数类比物理学中的熵，主要反映地块自身多种类用地的混合程度。同样地，土地利用混合度系数无法反映交叉口周边范围内各个地块的土地利用混合度系数的强弱次序。不同于Mi的变化区间较大，Wi的变化区间只有（0，1］，故在设计公式时，做了平方项处理。本文以i 地块的土地利用混合度系数的平方项和x 个地块中最小的土地利用混合度系数的平方项min() 的比值，作为i 地块土地利用混合度修正系数γi。

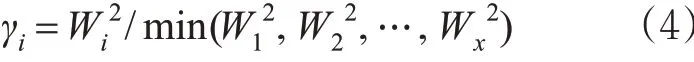
γi的取值范围为［1，+ ∞）。当Wi是整个交叉口所有地块土地利用混合度系数的最小值时，γi等于1。当i 地块的土地面积构成正常，而其他地块的土地面积均趋于0 时，γi趋近于正无穷大。事实上在现实生活中，γi常常在1～2 之间波动。当γi大于1时，表明i 地块的土地利用混合度系数大于整个交叉口所有地块土地利用混合度系数中的最低值，该地块影响下的进口道上交通流受到的土地开发混合度干扰大于整个交叉口的最低值，因此需要对该进口道处的交通量进行放大处理。

1.4 土地利用融合修正系数计算

由前文分析可知，交叉口各进口道两侧的土地的利用强度、混合度不同，对交叉口各个进口道交通流带来的干扰也不同，为此，需要同时考虑土地利用强度修正系数和土地利用混合度修正系数的影响，为此，本文引入i 地块的土地利用融合修正系数δi见式（5）。

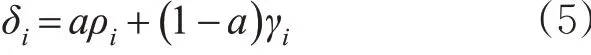
式中:a(0 ＜a ＜1) 为权重参数，与具体的交叉口具体的交通量相关，需根据具体情形进行标定。

土地利用融合修正系数与各个地块的土地利用强度修正系数、土地利用混合度修正系数相关，其取值范围为［1，+ ∞）。现实生活中，δi常常在1～2之间波动。当δi大于1时，表明i 地块影响下的i 进口道上交通流受到的土地干扰（来自土地开发强度、混合度）大，需要对该进口道处的交通量进行放大处理。

1.5 土地利用信号配时计算

当前的交叉口信号配时方法往往没有考虑交叉口周围土地开发因素的影响。本文利用各个地块的土地利用融合修正系数修正其对应进口道的交通量，并以修正后的交通量作为经典的Webster 模型的输入量，得到考虑土地利用的信号配时方案，其基本步骤如下。

1） 计算交叉口设计交通量。 i 进口道n 流向的设计交通量qin为

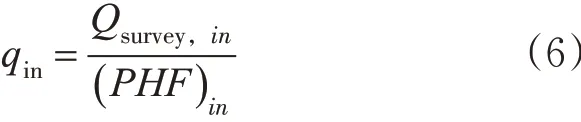
式中:Qsurvey,in为配时时段中i 进口道n 流向的调查交通量，pcu/h；( )PHFin为配时时段中i 进口道n 流向的高峰小时系数，主进口道取0.75，次进口道取0.8［23］。

2） 计算交叉口饱和度。根据HCM2010［12］计算交叉口的实际饱和流率，将进口车道划分成不同的车道组，第s 相位的饱和流率Qs为

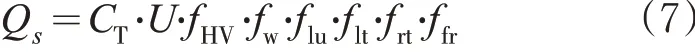
式中:CT为单车道理想饱和流率，一般取值为1 500 pcu/h；U 为车道组的车道数量；fHV为交通组成修正系数，其赋值与车道组交通流量中的重型车的百分比相关；fw为车道宽度修正系数，以车道宽度3.6 m 为界限，超过3.6 m 则修正系数大于1，反之则小于1；flu为车道利用修正系数，其赋值与车道利用程度相关；flt为左转修正系数，其赋值与左转车的比例相关；frt为右转修正系数，其赋值与右转车的比例相关；ffr为横向干扰修正系数，其赋值与行人干扰程度相关。

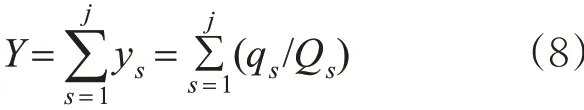
式中:Y 为周期内所有相位的关键车道组的流率比之和；ys为第s 相位的关键车道组的流率比；j 为相位数量；qs为第s 相位的关键车流量，pcu/h。

3） 计算修正交通量。在交通量修正计算中进口道设计交通量qin与i 地块是相互对应的。且1个进口道的3 个不同流向的交通量都对应同1 个土地利用融合修正系数。 i 进口道n 流向的修正后的设计交通量q'in为

式中:L 为交叉口损失时间；ls为第s 相位的启动损失时间，一般取3 s；As为第s 相位末的黄灯时间，一般取3 s；rs为第s 相位的全红时间，一般取2 s；Is为第s 相位末的绿灯间隔时间。

5） 计算信号周期。信号周期计算公式为

式中:C 为信号周期，s。

6） 计算绿信比。绿信比是交叉口信号周期中有效绿灯时间与信号周期时长的比值。绿信比按照各个相位的关键车流流量比之间的比例进行分配，计算公式为

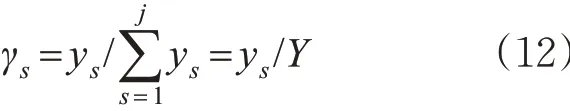
式中:γs为第s 相位的绿信比。

7） 计算交叉口有效绿灯时间。对于信号周期内任意第s 相位的有效绿灯时间gE,s为

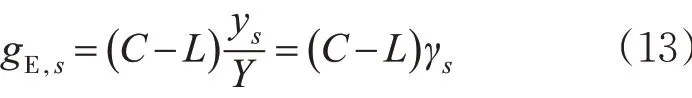
8） 计算交叉口显示绿灯时间。对于信号周期内任意第s 相位的显示绿灯时间g 为

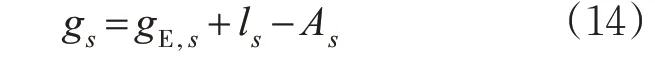
9） 行人过街时间检验。最短绿灯时间的设置是为确保行人能安全过街，通常以行人过街所需要的绿灯时间作为依据来确定最短绿灯时间，如果不满足要求则需要返回式（11）调整信号周期，行人过街最短绿灯时间gpedestrian为

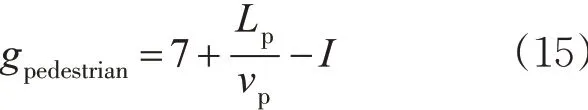
式中:I 为绿灯间隔时间；Lp为行人过街长度，m；vp为行人过街步行速度，一般取1.2 m/s。

2 基于GA的土地利用融合参数优化

2.1 目标函数

前文得到的基于土地利用的信号配时方案是关于权重参数a 的函数。本文信号配时目标是使得交叉口各个进口道的车辆延误总和最小。因此，可以以该车辆延误总和最小为目标，优化确定具体的权重参数a ，用以确定土地利用融合修正系数δi，最后得到完整的配时方案。

基于Webster方法，交叉口车辆中延误为

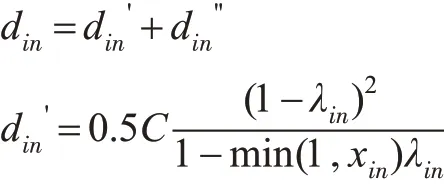
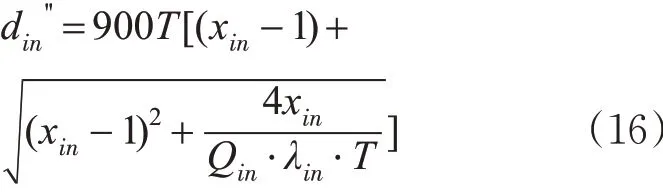
式中:din为i 进口道n 流向车道的每车的平均信控延误；din' 为i 进口道n 流向车道的每车的均匀延误；din''为i 进口道n 流向车道的每车的附加延误；xin为i 进口道n 流向的饱和度；λin为i 进口道n 流向车道的绿信比；Qin为i 进口道n 流向车道的饱和流率；T 为分析时段的持续时间，h，一般取0.25 h。

则基于土地利用融合修正系数优化模型的目标函数定义如下。

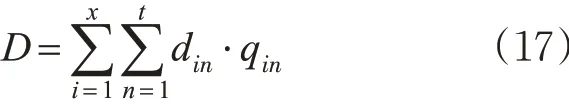
式中:D 为交叉口分析时段T 内各个进口道各个车道的车辆延误总和；t 为交叉口的流向数量。

2.2 约束条件

1） 权重参数约束。权重参数a 反应的是土地利用强度修正系数在土地利用融合修正系数中的权重，是非负值且应小于1。

2） 周期长度约束。交叉口的周期长度是所有相位的总绿灯时间和总损失时间之和，为确保交叉口正常运行，设置最短周期和最长周期。

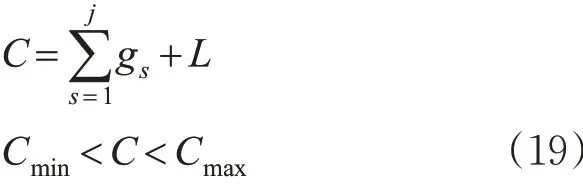
式中:gs为第s 相位的绿灯时间；Cmin为最短周期时长，一般取值60 s；Cmax为最长周期时长，一般取值180 s。

3） 绿灯时间约束。为确保各个相位车辆的安全运行，需要设置最短绿灯时间和最长绿灯时间。

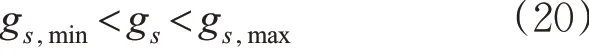
式中:gs,min为第s 相位的最短绿灯时间，一般取值15 s；gs,max为第s 相位的最长绿灯时间，一般取值60 s。

2.3 优化求解算法设计

土地利用融合修正系数优化模型如下。

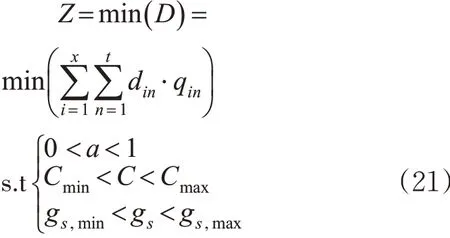
本文采用遗传算法（genetic algorithm，GA）进行求解上述模型。GA 是基于生物进化领域优胜劣汰的遗传机制，利用随机搜索的一种启发式算法。该算法将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程，在求解较为复杂的优化问题时，通常能够较快地获得较好的优化结果。应用遗传算法时，需要一定的代码来表示问题的解，本文采用二进制编码规则对可行解进行编码，各个染色体上有1 个基因，即对应的待估计的权重参数a 。

遗传算法流程见图2。

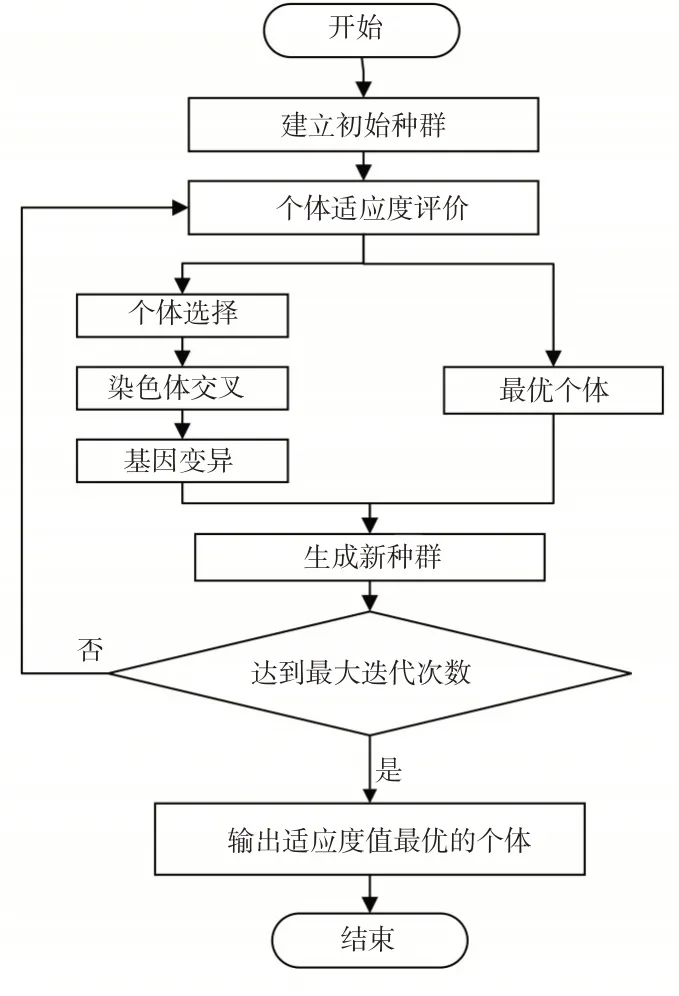
图2 遗传算法流程Fig. 2 Process design of GA

步骤1。建立初始种群。为保证种群中个体的差异性和多样性，本文初始种群规模为100。

步骤2。个体适应度评价。通过适应度函数可以评价个体的优缺点。它直接影响计算速度和结果的可靠性。在参数优化过程中，利用适应度函数筛选信号配时方案。以目标函数的倒数作为适应度函数。当目标函数值越小时，适应度值越大，被选择的概率也就越大。适应度函数（Fitness）的计算公式为

步骤3。个体选择。采用轮盘赌法，根据各个个体的适应度值决定其保留概率。第n 个个体的适应度为fn，种群整体的适应度之和为，则第n 个

步骤4。染色体交叉。染色体交叉概率为0.99，根据约束条件判断个体的可行性，若为无效的个体，则继续执行交叉直到生成有效的个体。

步骤5。基因变异。基因变异概率为0.01，根据约束条件判断个体的可行性，若为无效的个体，则继续执行变异直到生成有效的个体。

步骤6。检验是否达到最大迭代次数500，如果满足则执行步骤7；如果不满足则执行步骤2。

步骤7。输出种群中适应度值最优的染色体作为问题的满意解或者最优解。在种群个体中出现最优解或达到设置的停止准则时，结束优化过程，并输出当前个体中的最优解。

通过遗传算法输出的适应度值最优的个体即为需要标定的权重参数a 。计算得出权重参数a 后，带入式（5）求解i地块土地利用融合修正系数δi。然后按照式（6）～（14）计算求解优化的信号配时方案，并通过式（15）检验行人过街最短绿灯时间。

3 案例设计

3.1 交叉口现状

以江苏省徐州市丰县“人民路-工农路”交叉口为研究对象。人民路（ Lp为12.5 m）是东西方向的主干路，工农路（ Lp为14.7 m）是南北方向的次干路。4个进口道均有1条左转车道，1条直行车道和1条右转车道。除北进口道车道宽度为3 m 以外，其余进口道车道宽度均为2.9 m。东、南、西、北4个进口道长度分别为638，485，639，423 m。该交叉口地处丰县传统县城中心，整体片区地块主要是商业、居住混合，兼有部分公共设施。该交叉口为十字交叉口，为方便描述将周边土地从北到南、从西到东，依次划分为A，B，C，D 这4 个地块。该交叉口的车道分布及地块划分见图3。

当前该交叉口原始方案为4相位控制，第1相位为东西方向左转；第2 相位为东西方向直行；第3 相位为南北方向左转；第4 相位为南北方向直行。交叉口信号相位见图4。

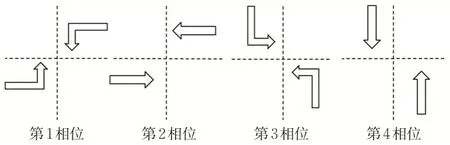
图4 交叉口信号相位图Fig. 4 Signal phase diagram of intersection

3.2 交叉口交通状况

针对选定交叉口，选取2018 年8 月该交叉口2组不同时段的交通流数据，见表2。

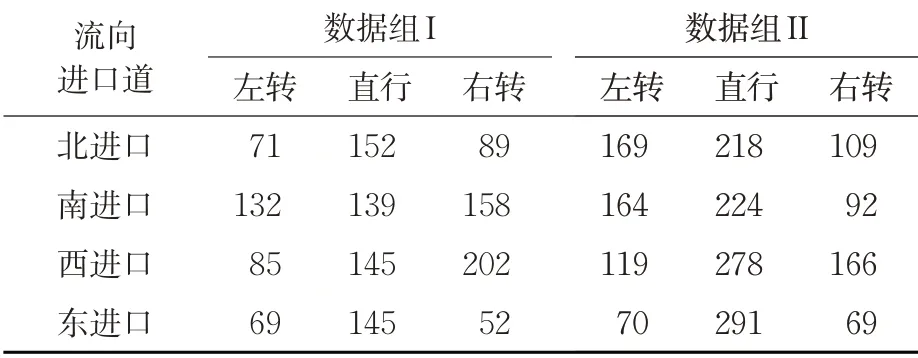
表2 交叉口调查交通量表Tab. 2 Survey traffic volume of intersection pcu/h

在交通调查时发现该交叉口较为拥堵，主要原因是三轮车等非机动车过多，车道狭窄，行人混行现象严重。另外，在数据组I调查时，南进口、西进口的右转车比例较高，虽然有专用的右转车道，但是仍然给交叉口带来了较大的延误。在数据组II 中，左转车比例较高，左转车道出现了一定的拥堵状况。

3.3 土地利用指标计算

将该交叉口周围土地划分为居住用地、商业用地、公共设施用地等用地类型，见图5。

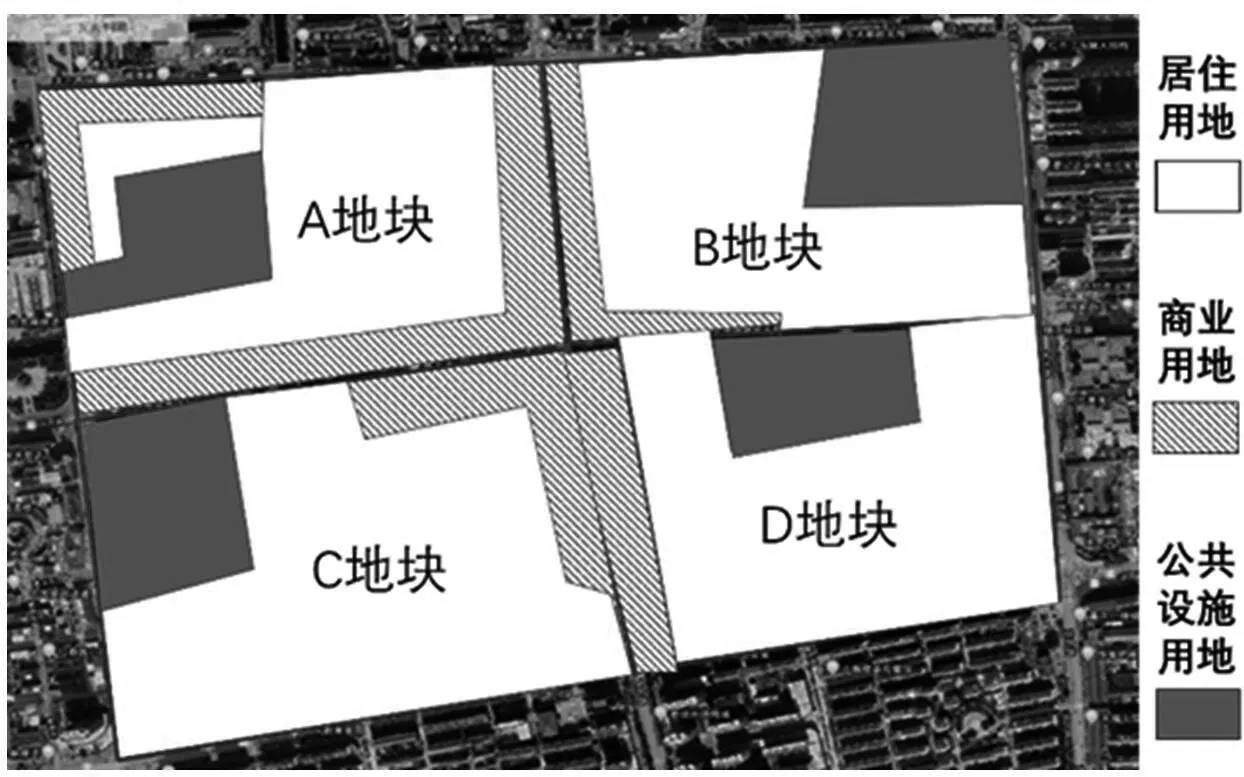
图5 交叉口地块用地分类图Fig. 5 Land classification map of intersection plot

土地容积率参考文献［22］，土地面积依据百度地图测量，地块土地利用信息整理见表3。

4个地块的主体部分为居住用地，其中B，C这2个地块上的住宅的容积率较高，存在多处高密住宅群，且B，C 地块的居住用地面积相对较大，故B，C地块的土地开发强度较大，其对影响下的东进口、西进口的干扰应该是所有进口道中较强的；同时，相比A，B地块，C，D地块的土地开发混合程度较大，其对影响下的西进口、南进口的干扰应该是所有进口道中较强的；具体的土地利用对交通量的影响需要后续的土地指标计算。

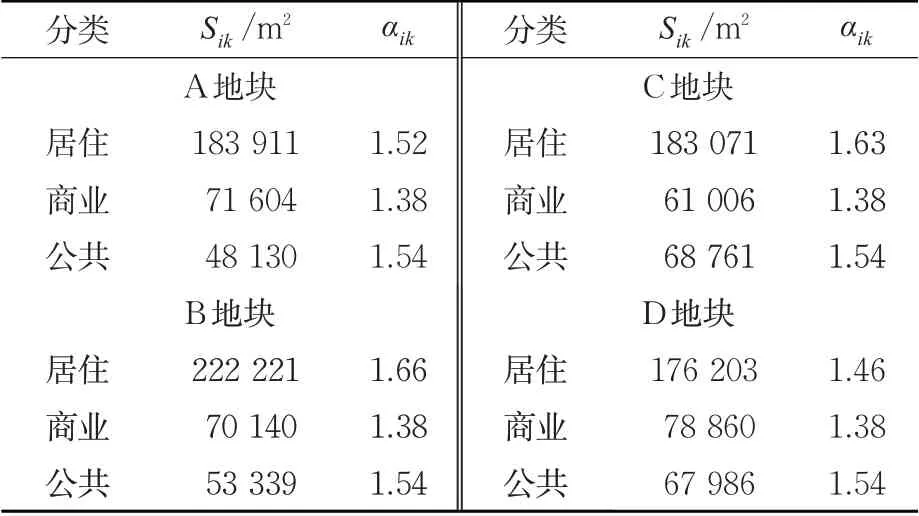
表3 交叉口地块土地利用信息表Tab. 3 Land use information of intersection plot

依据表3 和式（1）、式（2）计算各地块土地利用强度系数Mi、土地利用混合度系数Wi，并按照式（3）、式（4）计算各地块土地利用强度修正系数ρi、土地利用混合度修正系数γi，数据整理见表4。

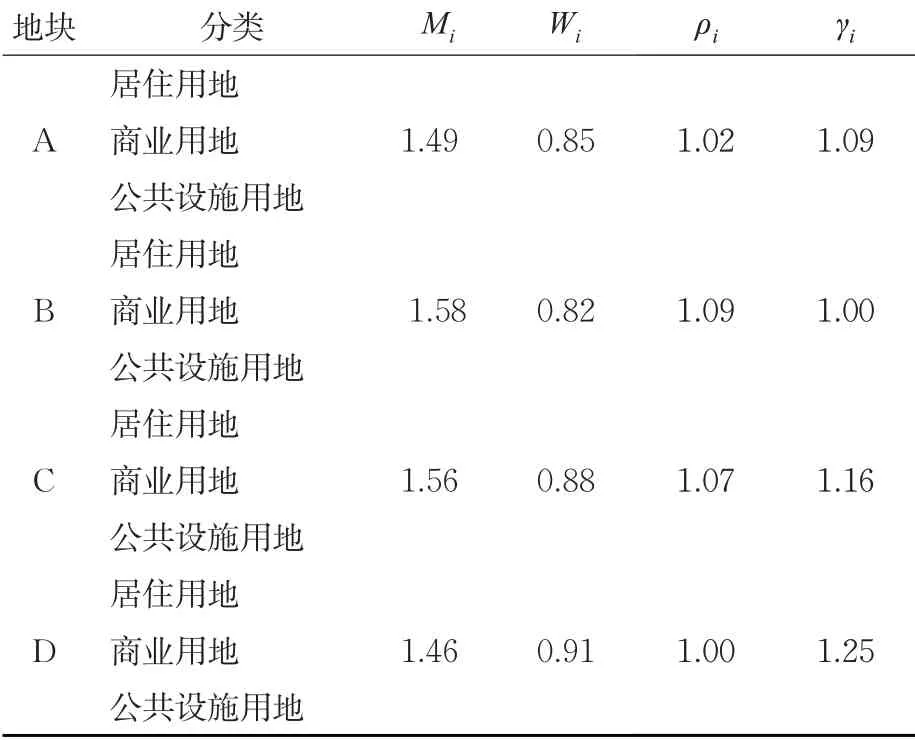
表4 交叉口土地利用指标表Tab. 4 Land use indicators of intersection

由表4可知:①B，C，A，D的土地利用强度修正系数依次递减，其分别对应的东进口、西进口、北进口、南进口受到来自土地开发强度的干扰也是依次递减；②D，C，A，B的土地利用混合度修正系数依次递减，其分别对应的南进口、西进口、北进口、东进口受到来自土地开发混合度的干扰也是依次递减；③当各个进口道对应的土地利用强度修正系数（或者土地利用混合度系数）大于1时，该进口道的交通量需要在配时中放大处理，但是由于2 个指标融合的权重参数a 未知，具体的数值需要结合具体交叉口交通量进行后一步分析计算。

3.4 信号配时计算

按照式（6）计算i 进口道n 流向的设计交通量qin，数据整理见表5。

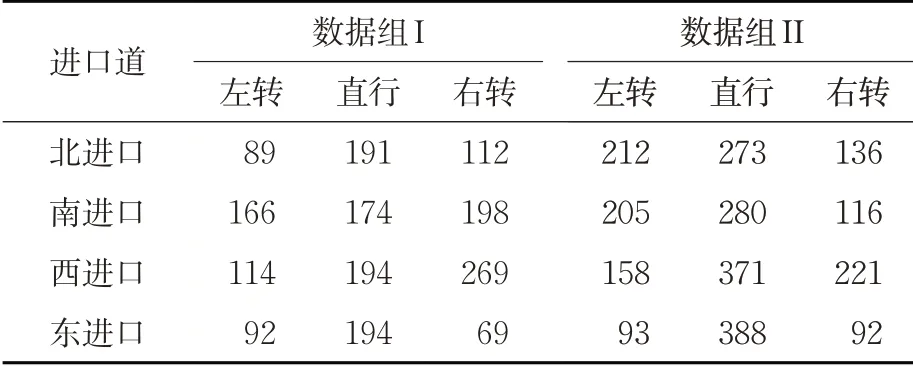
表5 交叉口设计交通量表Tab. 5 Design traffic volume of intersection pcu/h

应用前文中的基于GA 的模型优化算法，并借助Matlab 求解交叉口在一组交通量数据、二组交通量数据中的权重参数a 。一组数据的权重参数a 是0.942 0，二组数据的权重参数a 是0.742 6。将其分别代入式（5）求解2 组数据的土地利用融合修正系数，计算结果见表6。

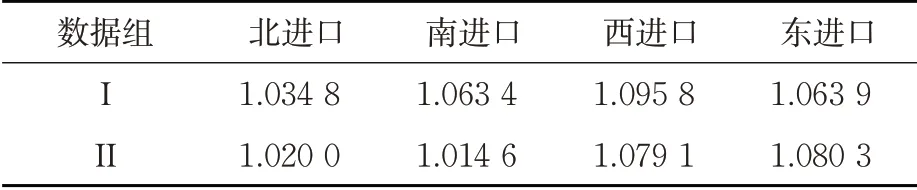
表6 土地利用融合修正系数表Tab. 6 Table of land use integration correction coefficient

按照式（9）计算i 进口道n 流向的修正后的设计交通量q'in，数据整理见表7。

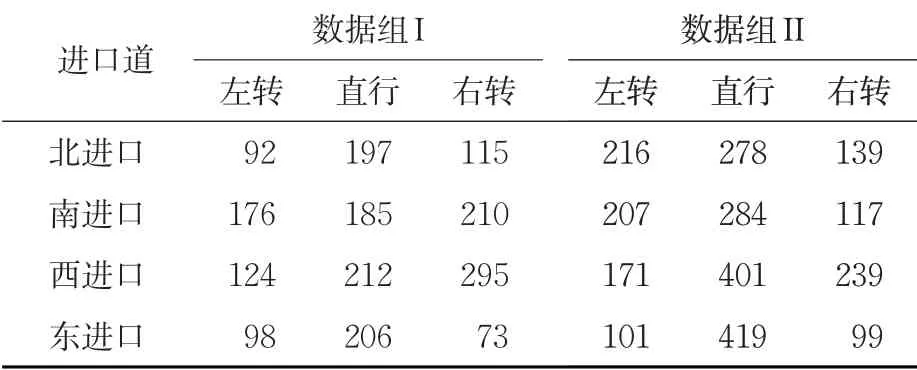
表7 交叉口设计交通量表（修正后）Tab. 7 Design traffic volume of intersection （revised）pcu/h

分别以表7中交通量作为输入值，依据式（10）～（14）计算求得交通量修正后的优化信号配时方案（简称:优化方案）。其中各相位黄灯时间、全红时间均分别取为3 s和2 s，相位设计同图4，交叉口优化配时方案见表8。

因为依据式（10）各相位绿灯间隔时间均为5 s，按照式（15）反推最小绿灯时间为

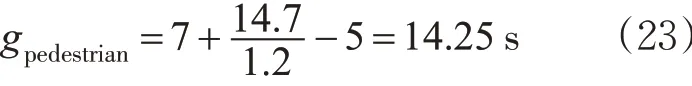
计算结果gpedestrian=14.25 s ，小于表8中最小的绿灯时间22 s，即可知表8 中绿灯时间全部满足行注:gs为第s相位绿灯时间；C 为周期长度。人最小过街时间检验要求。

表8 交叉口优化配时方案Tab. 8 Optimal timing scheme of intersection

4 仿真评估

4.1 仿真建模

利用Vissim 软件分别建立交通仿真模型模拟交通流的运行状况。为保证控制变量原则，仿真中交通量赋值均为表2中的原始调查交通量，唯一改变的是信号配时时间。仿真时间为0～3 600 s，仿真计数间隔为1 s。按照东、南、西、北的顺序，在4 个进口道所有车道设置了监测点，交叉口仿真示意见图6。

图6 交叉口仿真示意图Fig. 6 Simulation diagram of intersection

4.2 仿真方案选择

为了更好地检验本文方法的有效性，选择以下2组共计5种信号配时方案进行仿真。

实验组:本文基于土地利用的信号配时方案（简称:优化方案），即表8中的数据组I、数据组II这2种信号配时方案。

对照组:①交叉口当前的原始信号配时方案（简称:原始方案）；②普通的Webster 方法的信号配时方案（简称:普通方案），即根据表5计算的数据组I、数据组II这2种信号配时方案。对照组的配时方案见表9。

4.3 评价指标选取

本文选用4项性能指标对交叉口信号配时进行评价:①平均行程时间，其表示交叉口驾驶员的出行时间总值的均匀分布；②平均延误时间，其表示车辆通过交叉口所需时间与遇到障碍物时在同一距离正常行驶所需时间之差；③平均停车时间，其表示车辆占用交叉口车道而不在行驶状态的时间；④平均停车次数，其表示车辆通过交叉口时在信号控制的影响下停车次数。

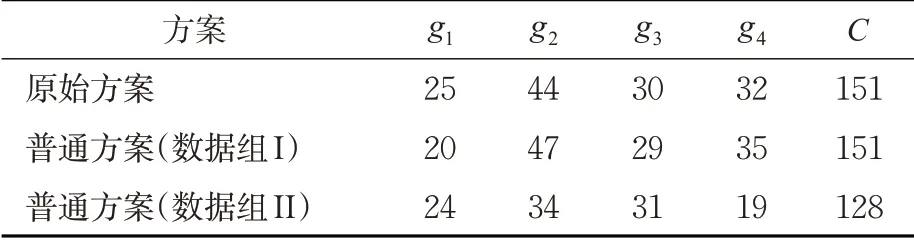
表9 交叉口对照组配时方案Tab. 9 Intersection timing scheme of control group s

4.4 仿真结果分析

在对上述5 种信号配时方案进行10 次仿真后，通过取平均值的办法，获取了各项评价指标数据，处理见表10。

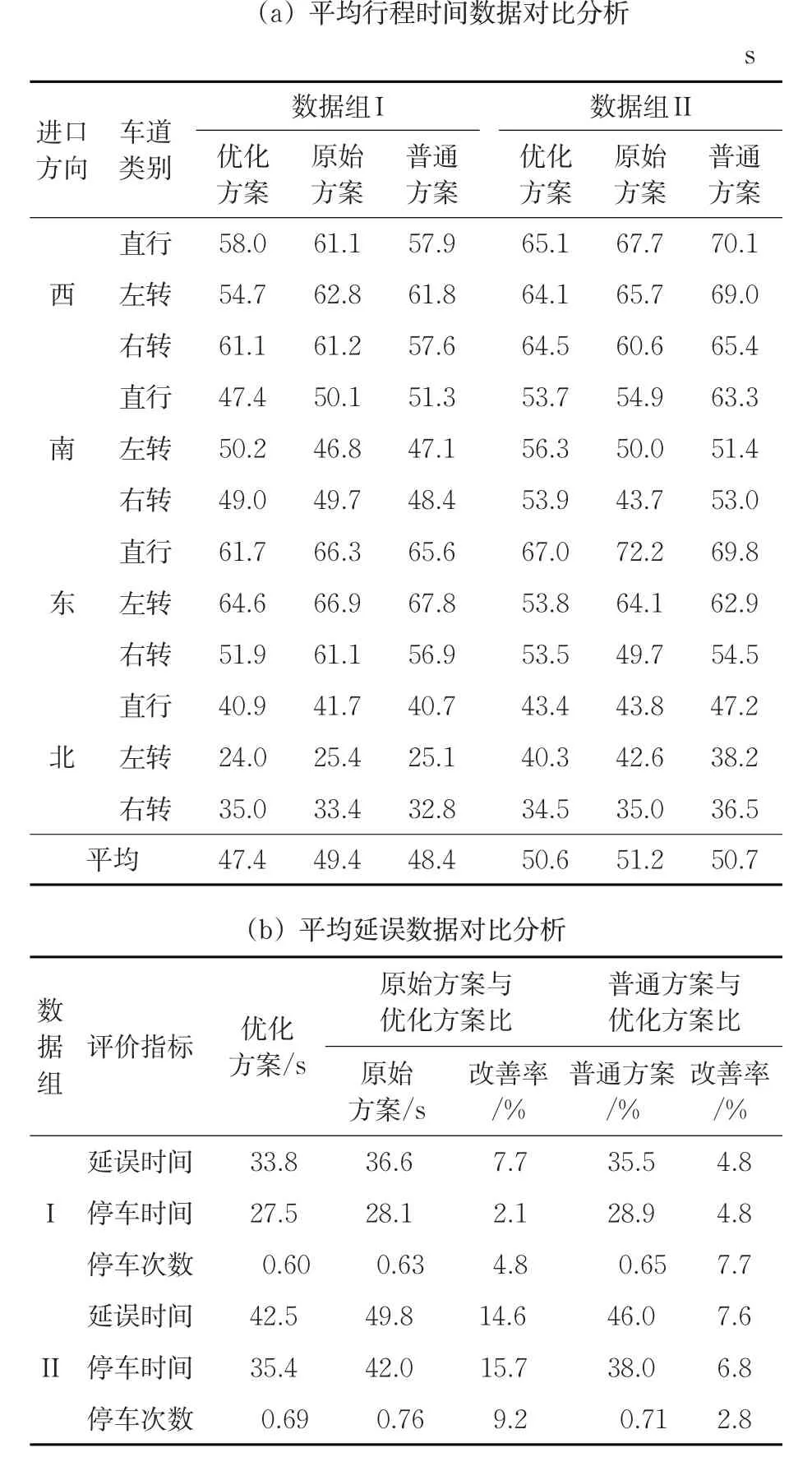
表10 评价指标对比表Tab. 10 Comparison table of evaluation indexes

由表10 可以看出:①由平均行程时间数据可知，主要的平均行程时间的缩减集中在西进口、东进口上，这与表6 相对应，表6 中在这2 个进口道上的土地利用融合修正系数较大，这说明本文的考虑土地利用的方法能够有效提高整体交叉口运行效率；②无论对于数据组I 还是数据组II，“人民路-工农路”交叉口的配时方案，在平均行程时间数据、平均延误数据这2类指标上，均是优化方案最佳（即考虑土地利用的信号配时方法），其次是普通方案（即普通的Webster信号配时方法），最后是交叉口的原始方案，这验证了本文考虑土地利用的单交叉口信号配时方法的有效性。

5 结束语

为实现基于土地利用的信号配时控制，本文提出一种考虑土地利用的单交叉口信号配时方法。该方法量化土地利用指标成修正系数，用以优化城市单交叉口原始交通量，得到考虑土地利用的修正后的交通量数据，随后利用Webster 信号配时方法获取新的配时方案。本文以徐州市实际交叉口为研究对象，构建单交叉口仿真模型，采用实际交通流数据，分析考虑土地利用的交叉口信号控制的性能，证明了本文提出的配时方法的有效性。同时，仿真结果表明:①本文方法的优势在于以数量化的形式定义了土地利用对交通流的干扰，且在配时流程中通过放大交通量的形式，有效地体现了不同土地开发情况对交叉口信号配时的影响，②本文方法可以随着交叉口交通量的变化而动态调整土地利用融合系数中的权重参数a ，动态地引入土地利用因素，实现考虑土地利用的实时单点交叉口信号配时。在后续研究中，可采集海量交叉口周边土地数据，构建区域类型的城市土地利用对交通信号的影响研究，实现由点到线、由线到面的层层递进。