基于时段偏好的高速铁路列车停站和频率优化*

黄志鹏 牛惠民

（兰州交通大学交通运输学院 兰州730070）

0 引 言

高速铁路作为一种安全、快捷、绿色的交通方式受到越来越多旅客的青睐。旅客选择高铁出行不仅仅局限于传统的铁路客运产品——位移，同时对列车服务提出了新的更高要求，而列车出发时段则是旅客最为关心的服务品质。旅客通常会根据各自的出行目的和出行习惯选择最理想的出发时段，即旅客对1 d 中的不同时段表现出明显的偏好和差异，这必然会导致旅客需求分布的时间不均衡。对应地，铁路部门必然会感受到这种偏好，并在不同时段提供不同的列车服务以响应这样的需求分布特征。在列车运营阶段，列车停站方案和开行频率是铁路供给产品的最重要体现，在很大程度上决定列车服务的品质。因此，深入研究旅客出发时段偏好和需求分布之间的耦合关系，据此优化高铁列车停站方案和开行频率，具有重要的现实意义。

轨道列车停站和频率优化始终是国际热门的研究问题。许多学者将列车停站方案作为列车运行图的子问题进行研究，Yue等[1]、Qi等[2]分别构建了以运输收益最大、列车空座位运行距离以及列车总停站次数最小为目标的规划模型，Shang等[3]将旅客出行过程抽象到基于空间-时间-状态的3维网络中优化列车停站方案。李得伟等[4]、牛丰等[5]将列车停站次数作为优化目标或者约束条件，构建高铁列车停站方案模型。Niu等[6]针对1条拥挤的高铁走廊，以最小化乘客的候车时间为目标，研究了列车时刻表和停站方案的协同优化问题。文献[7-8]以铁路运输企业运输效益最大化为目标对列车开行方案进行优化。文献[9-11]分析了影响旅客出行满意度的因素，并构建了列车开行方案模型。Wang[12]和Zhao 等[13]分析了旅客出行选择行为和列车开行方案优化的关系，并设计了优化模型和算法。考虑到需求与供给之间的博弈关系，文献[14-18]建立了双层规划模型对列车停站和频率问题进行数学描述，取得了重要的研究成果。

国内外学者对轨道列车停站和频率问题做了大量深入的研究，但如何在优化过程中体现旅客对出发时段的偏好属性，尚未见到公开的报道。本文针对1 条高速铁路走廊，引入吸引度与排斥度来量化旅客对出发时段的偏好，据此构造了新的高铁旅客出行阻抗函数，通过构建双层规划模型反映企业和旅客的不同利益博弈，研究基于时段偏好的列车停站和频率优化问题。本文的主要创新点是将旅客的出行时段偏好与列车停站方案和开行频率结合起来，将道路交通流平衡分配理论运用在轨道交通运输组织中，把多OD 客流需求分配问题转化为旅客出行方案（时空出行路径）选择问题。以期达到铁路运输企业运营“系统最优”和出行者“用户均衡”的协同优化。

1 问题分析

1.1 问题和假设

本文研究1条拥挤的高铁线路，拥挤性表现为受列车服务供给的影响，旅客不能全部按照自己最理想的时段出发。不失一般性，本文研究单方向列车的运营问题。设该高铁线路含有m 个车站，从始发站1开始，沿列车运行方向依次标记为2，3，…，m ，并用S 表示车站集合。

首先假设在给定的高铁线路上，所有列车的运行速度和编组长度相同。此外，假定高铁全天的运营时间限制在06:00—24:00之间，并以1 h为1个时段，按照时间顺序依次编号1，2，…，18，共18 个时段，如将07:00—08:00标记为时段2，并用H 表示时段的集合。

为了响应需求分布的时间不均衡特征，在不同时段，铁路部门会选用不同的停站方案及不同的开行频率或列车数量。本文将以时段为单元，依据旅客对出发时段的偏好，制定各时段的列车停站及频率方案，最大限度地满足具有时段偏好差异的旅客

需求。因此，本文研究的列车停站和频率问题，实际上就是确定集合为h时段开行p 停站方案的列车数量；P 为停站方案的集合。

1.2 时段偏好

从2 个方面度量旅客出发时段偏好，基于客观的时段吸引度和基于客流影响的时段排斥度。

1.2.1 时段吸引度

对于1 条运营的高铁线路，不同时段对旅客出发的吸引程度具有明显差异，其大小受出行目的、旅行时间、经济条件、文化习惯等多因素的影响。对于指定的车站i ，本文用1个介于0-1之间的常数来表示h 时段的吸引度。时段越好或该时段越吸引乘客，则吸引度的取值越小，反之则吸引度的取值越大。通常情况下，吸引度的取值可以通过旅客问卷调查或客流数据统计分析来获得。对于本文讨论的兰西高速铁路走廊（兰州西—西安北），在始发站（兰州西站）组织实施了含有1 067份有效问卷的数据调查，辅助于历史订票信息的分析，得到了该站的时段吸引度（见表1），其中时段4（09:00—10:00）最吸引乘客。

1.2.2 时段排斥度

对于某个出发时段，除了时段吸引度，还有一种受客流反向影响的属性，本文称之为时段排斥度，其大小受制于该时段加载的客流量。当某个时段的吸引度取值较小时，大量的旅客选择在这个时段出行，这必然会导致部分旅客买不到该时段车票，或者为了确保能在这个时段出行，旅客必须提前购票，使得出行灵活性降低，最终导致该时段的排斥度变大。

表1 兰州西站时段吸引度Tab. 1 Period attractivity of Lanzhouxi station

时段排斥度的数值，取决于从始发站发出的累计客流量。例如，车站对（1，2）关于时段1的排斥度，除了受时段1产生的（1，2）站之间客流影响，还要受时段1从始发站1发出的（1，3）、（1，4）、（1，5）等客流的影响和支配。基于此，用度量车站对间h 时段的排斥度。其中:xihj为变量，为从i 站出发途经车站对的累计客流量；为车站对( i,j )之间旅客能够在h 时段出发的数量，这与h 时段列车开行的数量有关。显然，累计客流量xihj越大，则该时段的排斥度越大。

1.3 阻抗函数

旅客出行的综合成本，可以用阻抗函数大小来度量。结合前文引入的时段吸引度和排斥度，本文定义车站对( )i,j 间旅客选择h 时段出行的阻抗函数见式（1）。

式中:α 为调节系数；τij为列车在车站对( i,j )的平均运行时间。式（1）定义的阻抗函数是累计客流量的增函数，具有普通阻抗函数的特征。

高铁旅客对出发时段的选择，类似于城市交通出行者对路径的选择，他们总是期望能够在阻抗最小的时段出行。不同于城市交通系统拥挤现象主要发生在行驶途中，高铁系统的拥挤现象则发生在上车站，表现为部分旅客不能够在自己期望的时段出发。

乘客首先会选择阻抗值最小的时段出行，当很多旅客都做出这种选择时，会导致该时段的阻抗增加，并使该时段不再是旅客最佳的选择，部分旅客会转而选择其他时段。如此循环反复，最终旅客对出发时段的选择达到UE 平衡状态。也就是说，所有时段上的出行阻抗相等，都等于它们共同的最小值。

1.4 停站方案

对于1 条含有m 个车站的高铁线路，列车将有2m种可能的停站选择。当m 较大时，这是1 个典型的NP问题。然而，现实中真正需要选择是否停车的车站数量往往并不太多。如始发站1 和终到站m ，以及部分客流量大的中心城市所在站，列车必须停车。排除这些必停站，需要决策是否停车的车站是很有限的。

如含有10 个车站的兰西高铁走廊，除兰州西、定西北、天水南、宝鸡南、咸阳秦都、西安北等6个必停站，真正需要选择列车是否停靠的车站只有4个。因此，全部停站方案的总数为:24= 16 。基于此，对于本文讨论的列车停站问题，可以用枚举法列出所有可能的方案，再用优化模型计算相应的列车频率。然而，当停靠车站增多时，这种建立列车停站方案备选集的方法会降低求解效率，应当增加1 组0-1决策变量来表示沿途停靠站的“停车/通过”状况。

1.5 求解思路

本文运用双层规划模型刻画问题，用遗传算法和Frank-Wolfe方法求解模型。在构模阶段，上层模型确定列车停站和频率方案，下层模型确定时段配流结果。具体地说，就是将全天的OD 客流需求作为输入常数，对枚举的每个停站方案和当前的列车频率，运用Frank-Wolfe 方法将客流需求加载至时段；然后，利用得到的配流结果，计算和度量方案的优劣，再运用遗传操作生成更好的列车频率；如此循环反复，最终得到最优的基于时段偏好的列车停站和频率方案。

2 模型和算法

2.1 符号说明

本文建模所需符号见表2。

表2 符号说明Tab. 2 Notation's description

2.2 上层规划

1） 目标函数。在一个出发时段，可以选用不同的停站方案和开行频率。这些不同的列车开行方案，必然产生不同的运营成本。本文以最小化铁路部门总运营成本为上层规划的优化目标。当第h 时段，选用停站方案p 的列车数量为yhp（决策变量）时，将产生rp⋅yhp的运行成本，对于铁路运输企业，运营成本最小化是其目标，故上层目标函数可以表示为

式中:θij为铁路部门为车站i 与j 之间分配的票额比例，假定该数值为已知的常数，取值可根据历史数据进行估计。约束条件（3）表示h 时段开行的列车总数不能超过额定能力，约束条件（4）表示车站i 与j 之间在h 时段提供的服务能力应该不小于相应的客流需求。

2.3 下层规划

旅客总是选择出行阻抗最小的时段出发，而阻抗函数（1）又是流量的增函数，这必然会导致不同旅客间的选择博弈，这种选择博弈最终会达到一种UE用户平衡状态。即对于车站对(i,j) 间的旅客，任意时段只要存在客流，则这些时段上旅客出行阻抗相等。用uij表示车站i 与j 之间的最小出行阻抗，则UE平衡条件可表示为

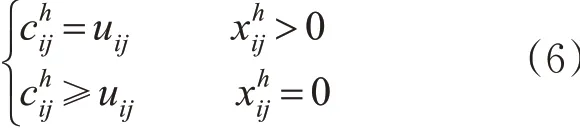
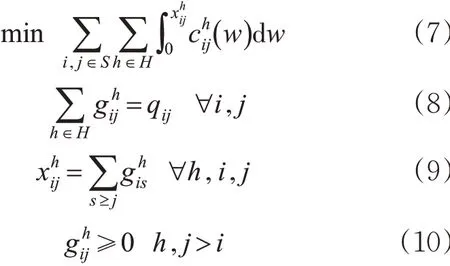
图1 算法流程Fig. 1 Algorithm process

上述最优化模型具有和城市交通UE 配流模型相似的形式，差异性表现在其中的路段、路径和阻抗函数具有完全不同的意义。其中决策变量表明在上层决策的基础上，流量分配的结果，其又能反馈给上层约束（4）。

2.4 算法

所建模型是1 个双层规划问题，它被公认为是极其困难求解的NP完全问题。目前，国内外学者普遍运用智能算法从全局角度寻找满意解。考虑到遗传算法编码与本文模型有较好的契合度，同时具有较好的全局收敛性。另一方面，所建的下层模型是在Beckmann 模型基础上进行的转化模型，而Frank-Wolfe 算法是目前广泛应用的求解Beckmann模型的有效算法。因此，采用嵌套Frank-Wolfe方法的遗传算法对双层规划模型进行求解。

遗传算法染色体采用整数编码，每个染色体表示1个可能的停站和频率方案。每个基因位置表示各时段各种停站方案的列车数量yhp。算法流程见图1。

3 算 例

3.1 参数设置

以兰西高铁走廊（见图2）为背景，对所提出的模型和算法进行测试。为了方便表示，按照列车运行方向依次编号1，2，…，10，并标记相邻2站间运行时分，如车站对(2,3)间运行时分为0.5 h。

图2 兰西高铁走廊示意图Fig. 2 Lanzhou-Xi'an high-speed-rail corridor

3.1.1 参数取值

对于上述单向列车运行问题，根据西兰高铁上行方向（兰州西—西安北方向）2025 年客流预测数据，并以目前西兰高铁上各OD 间的票额分配比例作为算例的输入。车站i 到车站j 之间的旅客出行需求qij、及票额比例 θij见表3。

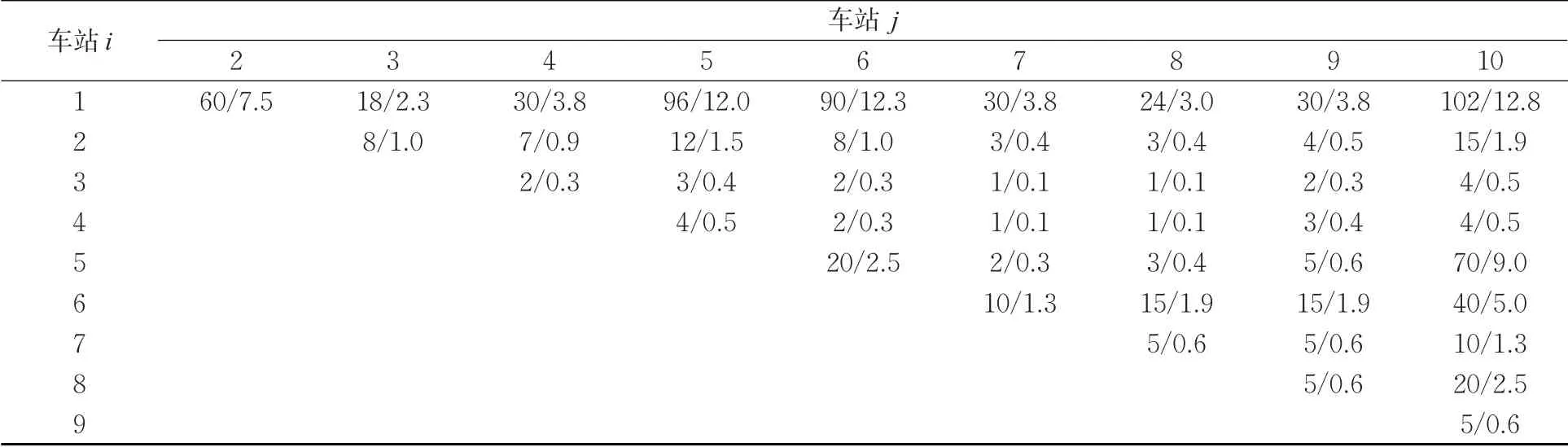
表3 参数qij 和 θij 的取值Tab. 3 Value of qij and θij

各时段均按最小发车间隔5 min 进行设置，即各时段的最大发车数fh均为12 列。列车定员按照CRH3C 型动车组，β = 601 。对于参数，可通过车站对( i,j )之间的列车运行时分τij可通过计算( i,j )之间的所有区间运行时分之和得到。不同停站方案下的列车运行成本rp见表4。考虑到兰西高铁沿线各站的时段吸引度相差不大，本文用兰州西站的吸引度（见表1）来替代所有车站的吸引度。此外，遗传算法中的种群规模popsize = 200 ，交 叉 概 率 Pc= 0.8 ，变 异 概 率Pm= 0.07 ，最大迭代次数为100代。

表4 参数rpTab. 4 Value of rp (unit: ten-thousand yuan/train)万元/列

3.1.2 参数α 的标定

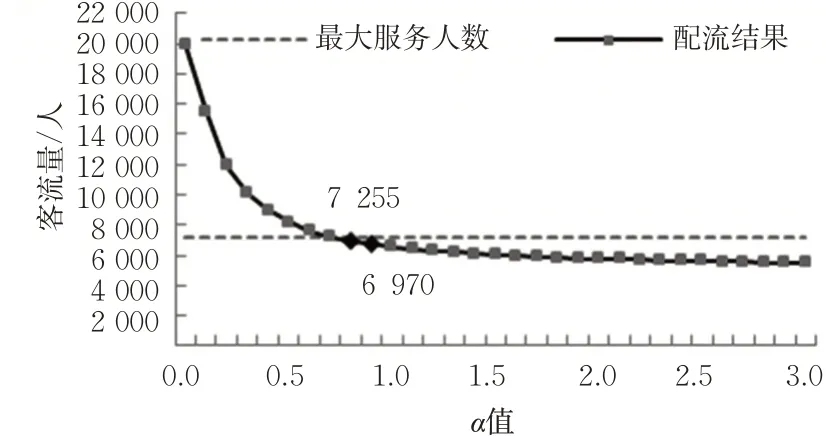
图3 不同α 值，时段4客流分配结果Fig. 3 Passenger assignment for period 4 with different α value

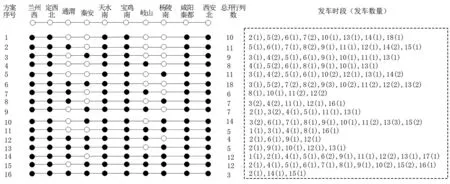
图4 列车停站方案及数量Fig. 4 Train skip-stop operations and quantities

3.2 计算结果

上层规划的优化结果见图4。图4的左侧，枚举了所有16种列车停站方案，右侧列出了各时段不同停站方案的列车数量。如第一行的方案1表示列车在通渭、秦安、岐山和杨陵南不停车，该方案全天开行10列，其中在第2时段开行1列、第4时段开行1列等。

下层规划的配流结果见表5，可得到各车站全天18 个时段的总出发人数。共有45 个车站对，表5 列出了部分车站对之间的流量分配输出。上述配流结果符合通常情况下旅客对出发时段的偏好，如旅客选择第4 时段（09:00—10:00）和第12 时段（17:00—18:00）的出发客流最大。

表5 各时段配流结果Tab. 5 Passenger assignment in each period人·次

图5 描述了吸引度、排斥度和客流量随时段变化的情况。吸引度曲线与排斥度曲线的走势相反，而排斥度曲线与客流曲线的走势相同，这与吸引度、排斥度的意义完全吻合，即出发时段越好，则吸引度取值越小，排斥度取值越大，所加载的客流也就越多。

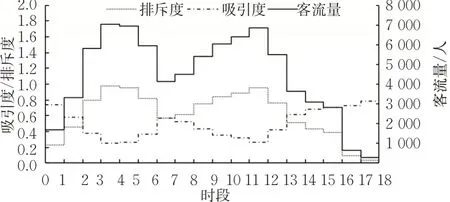
图5 各时段客流量、吸引度和排斥度Fig. 5 Passenger volume, attractivity and inaccessibility in each period

4 结束语

考虑到出发时段对高铁旅客出行决策的重要影响，利用吸引度与排斥度描述旅客对出发时段的偏好，并据此构造旅客出行阻抗函数。针对旅客和企业之间的不同利益博弈，建立了高速铁路列车停站和频率优化的双层规划模型，上层规划用于确定列车的停站和频率方案，下层规划用于计算客流分配结果。对所建立的双层规划模型，设计了嵌套Frank-Wolfe 方法的复合遗传算法。以兰西高铁为背景对模型和算法的有效性进行测试。计算结果表明:在可接受的求解时间范围内，本文提出的方法能够得到满意的高铁列车停站和频率方案。本文研究过程中，隐含着列车在时段分布均衡的假定。现实的高铁运营中，铁路部门为了响应旅客对出发时段的偏好，会考虑发车间隔不均衡的列车运行组织模式。如何优化基于时段偏好的列车服务方案，将是一个有意义的研究方向。