中弧线参数化曲线形式对压气机叶栅性能的影响

2020-12-29张馨艺羌晓青滕金芳余文胜

科学技术与工程 2020年33期

张馨艺，羌晓青，滕金芳，余文胜

(上海交通大学航空航天学院，上海 200240)

压气机是航空发动机的重要部件之一，航空发动机性能指标的不断提升，对压气机设计提出了更高的要求。叶片造型对发展高负荷和高效率等性能要求的压气机至关重要。

航空压气机叶片造型与叶片吸力面、压力面以及前尾缘连接处的光滑性息息相关。由于曲率特征不同，不同参数化曲线构造的压气机叶型存在着差异，进而影响压气机叶片气动性能。肖敏等[1-2]对超音压气机叶片中弧线设计方法做了大量的研究。Derksen等[3]基于使用多项式曲线和贝塞尔曲线等形式减少叶型设计自由度的思想，讨论了一种新的参数化叶型方法，拓展并改善了现有的贝塞尔参数化方法。

影响叶型气动性能的几何因素在于局部一阶和二阶曲率导数的变化。Yi等[4]研究了叶型局部轮廓变化对不同压力区域叶型气动性能的影响。研究结果表明，叶型型线一阶和二阶导数的变化会导致叶型气动性能参数的波动。局部一阶和二阶导数越大，空气动力系数的变化幅度越大。近年来，中外研究学者对保证曲率连续的叶型设计投入了大量精力。新的叶型设计方法在压气机和涡轮等叶轮机械上得到广泛应用[5-7]。宋寅等[8]使用曲率连续前缘对原始叶型进行优化后，抑制了前缘分离泡的产生，降低了叶型在大攻角工况下的总压损失。Korakianitisv等[9]提出了一种预置表面曲率分布的叶片设计方法，通过确保叶片表面前缘到尾缘的曲率和曲率斜率的连续分布，来优化叶轮机械叶片。相比原型，改型叶片气动性能和效率的提升显示了这种方法的有效性。

Nemnem等[10]提出了一种二维叶型生成工具。该工具采用立方B样条曲线控制中弧线二次导数，两次积分得到中弧线。给出的压气机叶片、涡轮叶片和风扇叶片的造型实例，验证了该方法的实用性和普遍性以及叶型光滑的重要性。

Sommer等[11]使用类似的方法，将基于曲率的方法和经典的中弧线厚度参数方法结合起来，提出了一种新型设计方法。叶片吸力面的型线通过给定的曲率分布(Bspline)数学积分后获得，叶片压力面的型线和中弧线通过叶片吸力侧坐标和厚度分布计算分析得到。这种方法可以不受限制地控制叶片吸力侧曲率，从而获得曲率连续的叶片吸力面和压力面。

研究表明，叶片型线的变化和曲率对叶片损失和气动性能有重要影响，然而关于中弧线参数化形式对压气机叶栅性能造成的影响却鲜有研究。将采用中弧线厚度法生成压气机二维叶型。中弧线厚度法是高压压气机叶片参数化的有效方法，其优势在于简单性和较少的设计变量。采用简单贝塞尔曲线、多项式曲线和曲率积分三种形式构造中弧线，对原型叶片进行改型设计，研究不同参数化曲线对叶型气动性能的影响。

1 研究对象与数值方法

1.1 研究对象

研究对象是高亚音速可控扩散叶片MAN GHH 1-S1，其几何参数和相关实验数据均由Steinert等[12]公开发表在文献上。二维叶型如图1所示。

b表示轴向弦长；c表示叶片弦长；t表示栅距；γ表示安装角； β1表示入口气流角；β2表示出口气流角图1 平面叶栅示意图Fig.1 Sketch of the cascade

叶栅的几何参数如表1所示，将原叶高为168 mm的叶片等比缩放至叶高为100 mm，缩放后叶片弦长为41.667 mm，安装角为30°。

表1 叶片几何参数

1.2 数值方法

采用计算流体力学软件NUMECA进行压气机叶栅的数值模拟，采用Autogrid5模块对研究对象进行结构化网格的自动划分，网格拓扑类型选定O4H，即叶片表面区域采用O型贴体网格，其余区域采用H型网格。平面叶栅的B2B(blade to blade)面网格分布如图2所示。数值计算采用Fine/Turbo模块，定常计算，工质为理想气体。空间离散格式采用中心差分格式。入口给定总温总压的边界条件，出口给定平均静压，壁面给定绝热无滑移的条件。

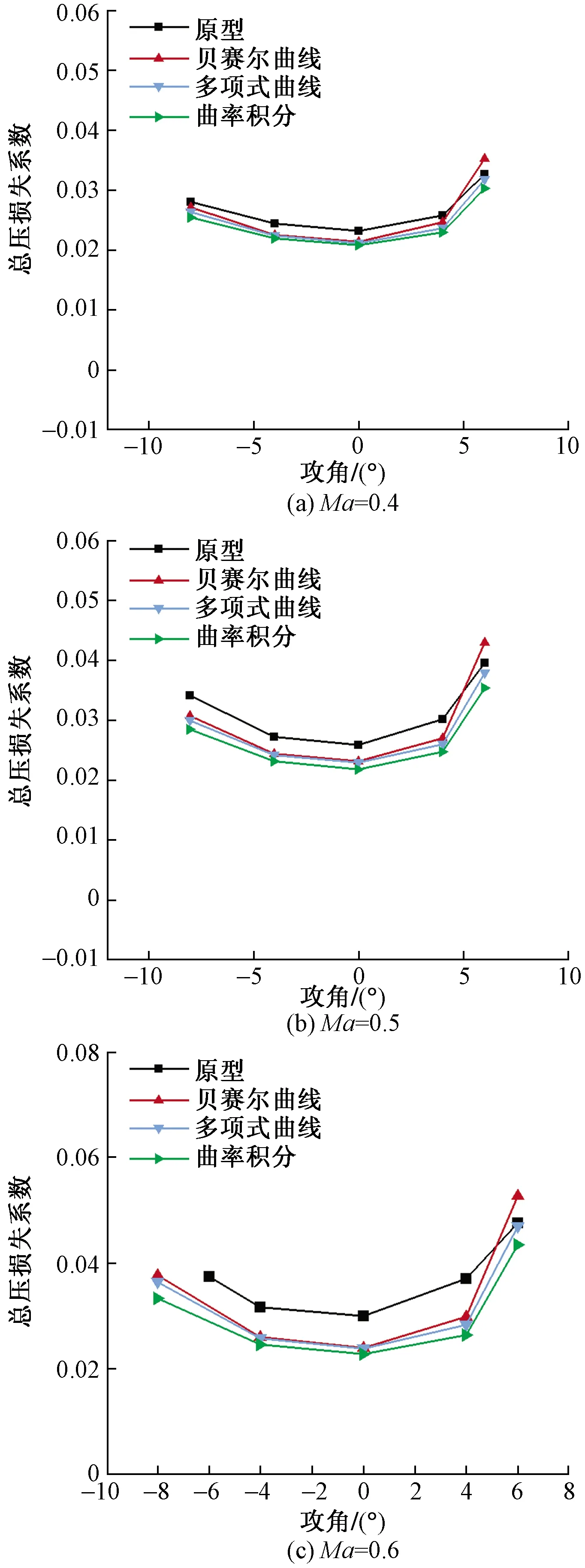
采用不同密度的网格研究B2B面网格拓扑结构的影响，分别设定单层网格数量为0.8×104、1.2×104、1.5×104、2×104、2.4×104，并根据网格密度调整第一层网格厚度，确保1

图2 B2B网格示意图Fig.2 Blade-to-blade surface mesh

1.3 数值方法验证

为了验证数值计算方法的正确性，将叶片表面中间叶高处的等熵马赫数分布与文献[12]中的实验值做比对。图3显示了4°攻角工况下叶片表面的等熵马赫数分布。

图3 4° 攻角下叶片表面等熵马赫数数值结果与实验值Fig.3 Experimental and numerical surface isentropic Mach number distributions at 4° incidence

从大体趋势上看，数值计算结果非常好地贴合了实验数据，只是在吸力面1/2弦长处误差较大，这可能与计算流体动力学(computational fluid dynamics，CFD)软件本身的计算模拟精确性以及湍流模型适用偏差有关。综上所述，数值计算结果与实验结果吻合度较高，计算方法可靠。

2 参数化方法

二维叶型的造型过程，首先是确定叶型的中弧线等主要几何参数，然后选择合适的原始叶型进行叠加。目前在压气机叶型造型中，广泛应用的中弧线形式主要有圆弧、多圆弧、抛物线及任意多项式等。3种中弧线的生成方式：①简单贝塞尔曲线；②多项式曲线;③3次非均匀B样条曲线控制曲率。

其中，简单贝塞尔曲线为二阶贝塞尔曲线，有3个独立的控制点。为了与压气机叶型设计参数关联，将基元叶型的几何进气角(β1)、几何出气角(β2)、轴向弦长(b)作为造型参数。多项式曲线采用拉格朗日插值法通过已知数据点来构建拉格朗日插值多项式，从而计算出插值数据点。

曲率积分中弧线方法则采用3次非均匀B样条曲线控制中弧线曲率沿弧长的分布，其中B样条曲线由6个控制点(P1～P6)确定，如图4所示。曲率分布经过一次积分以后即可得到叶型折转角沿弧长的分布，再一次积分以后获得中弧线型线。

图4 3次非均匀B样条曲线控制中弧线的曲率Fig.4 Curvature of camber line controlled by 3rd non-uniform B-spline

利用此造型方法一方面可以实现对曲率的直接控制，满足了精细化叶型控制的需求；另一方面中弧线曲率分布具有2阶可导的性质，保证了叶型中弧线的曲率高阶可导，有利于对流动的精细化控制。

3 参数化曲线的影响

以MAN GHH 1-S1叶型为原型，在保证进出口几何角、弦长及厚度分布均保持不变的前提下，分别使用贝塞尔曲线、多项式曲线、曲率积分曲线作为参数化曲线，对原叶型进行拟合，得到不同的中弧线参数化曲线方案。图5给出了3种参数化曲线得到的叶型几何对比。

图5 叶型几何对比Fig.5 Geometry comparisons of different profiles

3.1 原型叶型性能分析

在对压气机叶栅进行流场分析时，会进行总压损失系数ω的比较，其表达式为

(1)

图6给出了原型叶片在进口马赫数为0.4、0.5、0.6的情况下的攻角损失特性。

由图6可知，各马赫数下的总压损失系数都随着攻角增大而呈现先降低后增大的趋势，在入口马赫数为0.4时的叶栅损失系数在-4°～4°攻角范围内变化较为平缓，最小损失系数均在0°攻角处。在正大攻角工况，即高负荷阶段，叶栅损失迅速增加。

3.2 中弧线参数化曲线的影响

图7给出了进口马赫数为0.4、0.5、0.6时不同中弧线参数化曲线方案的叶栅总压损失系数随攻角的分布。由图7可知，不同进口马赫数下，不同的中弧线参数化曲线方案的总压损失系数随攻角的增大都呈现先减小后增大的趋势，且最小损失攻角都在0°附近。

图6 原型总压损失系数随攻角分布Fig.6 Variations of total pressure loss coefficients with different incidence angles

图7 不同进口马赫数时总压损失随攻角的变化Fig.7 Variations of total pressure loss coefficients with different incidence angles and inlet Mach numbers

随着马赫数增大，各方案的攻角范围均明显缩小。相较于原型叶栅，贝塞尔曲线方案的叶栅在正大攻角时总压损失急剧增大，多项式曲线、曲率积分这两种方案的叶栅损失在各攻角工况都有所减小，这种差异在较高马赫数(Ma=0.6)下尤为明显。总体而言，曲率积分方案效果最为显著，既拓宽了攻角适应性范围，且在各攻角工况降低了总压损失系数。

将从叶片表面等熵马赫数分布和流场结构等方面分析损失变化的原因。

图8给出了在0°攻角下，各叶型方案在进口马赫数分别为0.4、0.5、0.6时的叶片表面等熵马赫数分布。由图8可知，不同参数化曲线的中弧线对叶型的等熵马赫数分布有一定的影响，其中，3次多项式中弧线叶型和贝塞尔中弧线叶型的表面等熵马赫数分布几乎一致。曲率积分中弧线的叶型前加载现象最为明显，叶片在10%弦长附近载荷较大，尤其是在较高马赫数为0.6下较为明显。

图9将4种方案在6°攻角的马赫数分布云图进行比较和分析。从图9可以看出，相较于原型叶栅，曲率积分和三次多项式曲线方案的叶栅靠近尾缘区域的叶背分离损失减少很多，但是贝塞尔曲线方案的叶栅尾迹宽度与原型相比相差不大，这也解释了贝塞尔曲线方案叶型在正大攻角工况损失较大的原因。