基于神经网络的尾流激励叶片气动力辨识方法

张新燕， 刘 钊， 李金玖， 王沐晨， 张 珺， 李立州*

(1.中北大学机电工程学院， 太原 030051； 2.太原学院数学系， 太原 030001)

在航空发动机中，存在着随转动轴旋转的转子叶排和与机匣连接静止不动的静子叶排交错排列，两者之间存在轴向间隙。当发动机工作时，转子叶排与静子叶排之间产生相对转动，上游叶排的叶片尾流相对于下游叶排的叶片是一种随时间变化的非定常流动，会迫使下游流场的叶片发生振动，这是导致叶片疲劳损坏的原因之一。同时一些研究发现上游尾流也会影响下游叶片的气动弹性稳定性和颤振特性，影响叶片使用寿命[1-3]。因此，准确快速地预测上游尾流激励下的下游叶片气动力对航空发动机设计具有十分重要的意义。

随着计算机技术的发展，计算流体力学(computational fluid dynamics，CFD)方法成为研究叶片气动弹性振动问题的一种有效技术途径，但在应用时一些问题也随之而来，CFD方法在计算相对复杂的模型时计算时间十分长、计算效率较低[4-7]。为解决这些问题，Dowell[4]和Silva[5]提出了基于CFD技术的非定常气动力降阶模型(ROM)理论，在一定程度上代替了CFD方法研究非线性气动弹性问题，同时也在不低于CFD计算精度的情况下具有计算效率高、计算时间短的优点[13]。目前用于降阶模型的主要有谐波平衡法[7](harmonic balance，HB)、Volterra级数法[6]、本征正交分解技术(proper orthogonal decomposition，POD)[13]及神经网络模型[14-16]方法等。李立州等[6,17]利用基于系统辨识的Volterra级数方法建立尾流激励叶片气动力的降阶模型，可以较准确地描述下游叶片气动力振荡情况。罗骁[7]等提出了基于谐波平衡法的尾流激励的叶片振动降阶模型方法，算例表明该方法可以快速分析叶片气动力下的振动特性。近年来，越来越多的研究者将神经网络模型用于非定常气动力降阶模型的建模。Marques等[8]采用多层函数的神经网络法辨识二维翼型的非定常气动力，算例表明在有限的马赫数范围下该方法具有良好的预测能力。Diaconescu等[9]采用NARX递归神经网络预测混沌时间序列。王博斌等[10]运用带输出反馈的径向基函数神经网络建立非线性气动力模型，预测了气动力系数以及极限环颤振响应。Kou等[18]基于径向基函数神经网络，提出了一种多核神经网络的降阶模型方法，并将其应用于非线性非定常气动力问题。

将神经网络模型应用于上游尾流激励的叶片气动弹性振动问题。选择二维叶片模型作为算例，采用CFD计算模型获得训练信号和测试信号，分别用误差反向传播(back propagation，BP)神经网络和带外部输入的非线性自回归(nonlinear autoregre-ssive with external input，NARX)神经网络建立随机尾流激励下的叶片气动力模型，预测不同振幅的随机尾流激励和周期尾流激励下的叶片气动力，并与CFD模型计算结果进行比较，来进一步验证比较两种神经网络模型的性能。

1 基于神经网络的气动力建模

目前在系统辨识领域应用较为广泛的神经网络模型是BP神经网络，主要由输入层、隐含层和输出层组成[14-15]。BP神经网络的训练学习过程通过信号的正向传播与误差的反向传播来进行，输入信号从输入层进入网络，经过隐含层处理和传播，进入输出层；若输出层的结果与期望结果不同，则进入误差的反向传播过程，将误差传递给各层进行权值调整，直至误差达到预先设定的值，整个学习训练过程结束。BP神经网络是一种多层前向静态网络，无法准确描述系统的动态特性，NARX神经网络是一种动态神经网络，其网络结构相当于是在BP网络结构基础上引入输入延迟和输出反馈。

以二维叶片作为算例(图1)，该叶片气动力系统中，输入为尾流激励压力波，输出为叶片气动力(升力为C′l、阻力为C′d、力矩为C′m)，尾流激励的叶片气动力系统用行波法可简化表示为：{Cl(t),Cd(t),Cm(t)}=ψ{P(t)}(具体简化过程参见文献[6])。其中ψ表示叶片气动力系统中输入压力与输出气动力的对应关系，P(t)表示t时刻的进口总压。

采用图2所示的单隐层BP神经网络结构，建立尾流激励的叶片气动力辨识模型。其中，输入神经元个数为p，隐含层神经元个数为l，输出层神经元个数为q，输入层与隐含层之间的连接权值为v，隐含层与输出层之间的连接权值为w。

考虑到叶片气动力系统是一个弱非线性系统，在模型的输入层引入输入量的延迟，以时变尾流的进口总压P及其m阶延迟量作为模型输入xk(xk={Pk,Pk-1,…,Pk-m′}T)，分别以气动升力系数(Cl)、阻力系数(Cd)和力矩系数(Cm)作为模型输出yk。BP神经网络一般采用Sigmoid函数作为隐含层传递函数，输出层传递函数采用线性函数。那么，第j个隐含层节点的输出可表示为

(1)

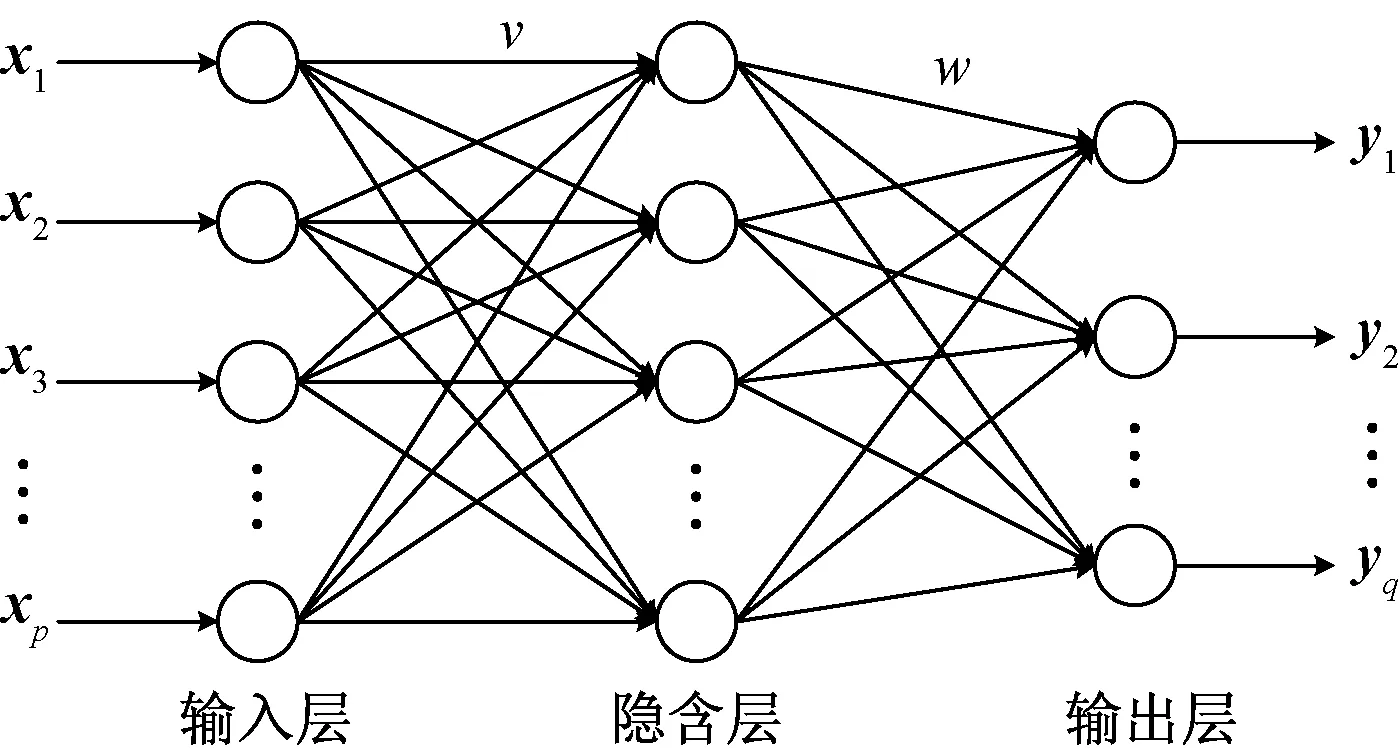
图2 BP神经网络的一般结构Fig.2 General schematic of BP neural network

则第j个输出层节点的输出可表示为

(2)

在BP神经网络的结构基础上引入输入延迟和输出反馈，得到图3所示的NARX神经网络结构，其表达式为

y(k)=f[y(k-1),y(k-2),…,y(k-n),x(k),x(k-1),x(k-2),…,x(k-m′)]

(3)

式(3)中：y(k)为神经网络的输出向量;n为输出向量反馈延迟长度;x(k)为神经网络的外部输入向量;m′为外部输入向量的延迟长度;k为离散时间，k=1,2,…,N;f表示神经网络模型。

图3 NARX神经网络的一般结构Fig.3 General schematic of NARX neural network

采用NARX神经网络建立尾流激励的叶片气动力辨识模型，采用串并联形式，以时变尾流的进口总压P作为神经网络的外部输入，分别以气动升力系数(Cl)、阻力系数(Cd)和力矩系数(Cm)作为神经网络的输出。当采用NARX神经网络计算叶片气动升力系数时，模型的输入可以表示为{Pk,Pk-1,…,Pk-m′,Cl(k-1),Cl(k-2),…,Cl(k-n)}T；计算叶片气动阻力系数时，模型的输入可表示为{Pk,Pk-1,…,Pk-m′,Cd(k-1),Cd(k-2),…,Cd(k-n)}T；计算叶片气动力矩系数时，输入可表示为{Pk,Pk-1,…,Pk-m′,Cm(k-1),Cm(k-2),…,Cm(k-n)}T。

采用神经网络模型辨识尾流激励下的叶片气动力的一般工作步骤如下。

(1)通过CFD模型计算不同尾流激励下的叶片气动力。

(2)选取其中一组尾流及气动力数据作为训练数据，以尾流压力波作为模型输入，叶片气动力作为模型输出，对神经网络进行训练。

(3)使用训练好的神经网络模型来预测其他尾流下的叶片气动力，并与 CFD 计算下的气动力结果进行比较，进一步验证该降阶模型的性能。

2 算例分析

采用流场CFD模型(图4)计算这两组尾流压力波在不同振幅时的叶片气动力，作为神经网络的训练数据及测试数据。设计两组不同的尾流压力波作为系统模型的输入，分别为随机尾流压力波(图5)和周期尾流压力波(图6)。二维叶片流场系统采用FLUENT进行求解，设置稳态出口压力为101 325 Pa，理想气体，计算模型为Spallart-Allmaras，计算初始温度300 K。尾流压力波以10 m/s的速度沿着进口y方向移动。

首先用一组随机尾流压力波及其叶片气动力作为系统模型的输入输出，对比验证BP网络和NARX

图4 二维叶片CFD模型Fig.4 CFD model of two-dimensional blade

图5 随机尾流压力波Fig.5 Random wake pressure waves

图6 周期尾流压力波Fig.6 Periodic wake pressure waves

网络的性能。如图5所示，设计一组减去稳态压力值的随机尾流激励压力波数据，即尾流压力波增量为ΔP(t)=random(t)5 000-2 500，单位：Pa。选定尾流压力波的稳态进口总压为120 500 Pa，采用CFD模型计算不同振幅的随机尾流压力波时[P=βΔP(t)]的叶片气动力系数，振幅系数(β)分别取为1.0、0.7、0.5、0.3、0.1、0.05。选择β=0.5的随机尾流压力波及其叶片气动力作为神经网络的训练信号，测试信号为β=1.0、0.7、0.3、0.1、0.05的尾流压力波及其叶片气动力。为了减少神经网络的训练时间，使用zscore函数对输入输出数据进行标准化处理。

采用BP神经网络建模时，引入输入延迟阶数m′=20，设置隐含层神经元个数为300；采用NARX神经网络建模时，引入输入延迟阶数m′=5，输出反馈延迟阶数n′=5，设置隐含层神经元个数为10；BP和NARX神经网络的训练算法均采用LM算法。首先用训练信号分别对BP网络和NARX网络进行训练，用训练好的BP网络和NARX网络模型分别对测试信号的叶片气动力进行预测，将测试信号的结果与CFD计算结果进行对比，结果如图7～图11所示。

图7～图11中，黑色点线基本被红色点线所覆盖，说明NARX神经网络对叶片气动力的辨识结果与CFD模型计算结果几乎一致，用随机尾流信号训练得到的NARX网络能够较好地辨识不同振幅随机尾流激励的叶片气动力。用随机尾流信号训练得到的BP神经网络模型预测叶片气动力，从图7～图11可以看出，在0～0.01 s这一时间段内蓝色点线与黑色点线均有明显偏差，振幅系数β=1.0、0.7、0.3、0.1、0.05的叶片气动力预测结果较好，振幅系数β=0.1、0.05的叶片气动力预测结果误差较大，说明用随机尾流信号训练得到的BP神经网络模型对于一定范围内不同振幅的随机尾流激励下的叶片气动力具有较好的预测能力，但其对于初始冲击阶段的叶片气动力预测效果较差。

图7 测试信号β=1.0的气动力结果对比Fig.7 Comparison of the aerodynamic results when β=1.0

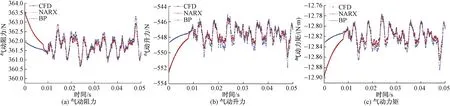
图10 测试信号β=0.1的气动力结果对比Fig.10 Comparison of the aerodynamic results when β=0.1

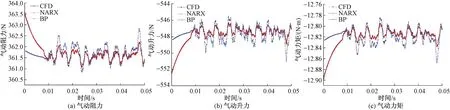
图11 测试信号β=0.05的气动力结果对比Fig.11 Comparison of the aerodynamic results when β=0.05

从算例可知，用随机尾流信号训练得到的NARX神经网络模型能很好地辨识不同振幅随机尾流激励的叶片气动力，不仅能较好地辨识振荡阶段的叶片气动力，也能较好地辨识初始冲击阶段的叶片气动力；而用随机尾流信号训练得到的BP神经网络模型的预测能力有限。

为了进一步探究BP神经网络模型和NARX神经网络模型对于不同尾流激励的叶片气动力的辨识效果及泛化能力，仍使用上面算例中经β=0.5时的随机尾流信号训练过的BP和NARX网络，来辨识周期性尾流激励的叶片气动力。

设计如图6所示的尾流压力波增量ΔP(t)，该波形不包含稳态压力，ΔP(t)是具有周期性的一组数据。探究随机信号训练的BP神经网络模型和NARX神经网络模型辨识不同振幅时周期性尾流激励的叶片气动力特性。尾流稳态进口总压仍为120 500 Pa，采用CFD模型计算振幅系数β=0.8、0.2、0.05的周期尾流压力波Δp′(t)激励下的叶片气动力系数，并以此作为测试信号，用随机信号训练的BP和NARX神经网络模型进行辨识。β=0.8、0.2、0.05时的叶片气动力辨识结果如图12～图14所示，并在图中给出了CFD模型计算的气动力进行对比。

图12～图14中可以明显看出，红色点线依然与黑色点线重合，说明用随机信号训练的NARX神经网络模型能很好地辨识不同振幅的周期尾流压力波激励下的叶片气动力；然而，蓝色点线已经与黑色点线完全偏离，说明用随机信号训练的BP神经网络模型对于不同振幅的周期性尾流压力波激励下的叶片气动力无法准确辨识。

从上述两个算例结果看，经训练得到的NARX神经网络模型比BP神经网络对于尾流激励下叶片气动力的辨识能力更强，计算精度更高。NARX神经网络模型经过一次训练，就可以辨识不同振幅下随机尾流压力波激励的叶片气动力以及不同振幅下周期尾流压力波激励的叶片气动力。而BP神经网络模型经过随机尾流信号训练后，只能辨识一定范围内的不同振幅下随机尾流压力波激励的叶片气动力且精度一般。

图12 测试信号β=0.8的气动力结果对比Fig.12 Comparison of the aerodynamic results when β=0.8

图13 测试信号β=0.2的气动力结果对比Fig.13 Comparison of the aerodynamic results when β=0.2

图14 测试信号β=0.05的气动力结果对比Fig.14 Comparison of the aerodynamic results when β=0.05

3 结论

基于BP神经网络模型和NARX神经网络模型，分别建立了尾流压力波激励下的叶片气动力辨识模型，并探究了这两种气动力辨识模型对于不同振幅随机尾流压力波激励的叶片气动力以及不同振幅周期尾流压力波激励的叶片气动力的辨识精度。二维叶片流场的两个算例表明：基于BP神经网络模型建立的尾流激励叶片气动力辨识模型，需要选择合适的训练信号来训练神经网络，才能预测一定范围内的尾流激励下的叶片气动力特性，该气动力辨识模型对于尾流激励下的叶片气动力辨识效果一般，有一定的局限性。基于NARX神经网络建立的尾流激励叶片气动力辨识模型，经过一次训练后，就可以辨识不同振幅的尾流激励下的叶片气动力，其辨识结果与CFD 计算结果基本一致，该气动力辨识模型对于尾流激励下的叶片气动力辨识精度高，泛化能力强。