孔隙式隔振系统非线性阻尼特性*
2020-12-29田浩男刘海超
闫 明, 田浩男,刘海超
(沈阳工业大学 机械工程学院, 沈阳 110870)
为避免冲击引起的破坏,舰载设备需要加装隔振系统.采用大阻尼粘滞阻尼器的隔振系统可以显著提高舰载设备的抗冲击性能.粘滞阻尼器装置结构简单、耗能效果好,广泛应用于航天、机械、军事等领域的隔振系统中,尤其是双出杆型液压缸式粘滞阻尼器克服了单出杆型阻尼器因真空效应产生的拉压力不均等弱点,可实现较大、较稳定的阻尼出力[1].
国内外学者对液压孔隙式粘滞阻尼器进行了研究,de Domenico等研究了非线性流体粘滞阻尼器耗能结构的抗震性能,在优化设计过程中采用了一种新的等能量非高斯随机线性化方法来处理非线性本构特性问题[2].van Tan等建立了某重型车辆的电子伺服阀液压阻尼器模型,阻尼器模型参数由试验数据确定[3].Singiresu提出在实际工程中按照基于周期内能耗守恒原则进行等效阻尼计算,使用等效阻尼系数和等效阻尼力替代液压阻尼器实际产生的阻尼力,但需要利用试验数据确定等效阻尼公式中的参数[4].孙靖雅等设计并制作了一种非牛顿流体粘滞阻尼器样机,从流体力学角度分析阻尼力机理,建立了改进幂律模型,并通过拟合试验数据获得待定参数[5].王琳等利用AMESim软件基于孔口流动原理建立了船用液压阻尼器的数学模型,将通过仿真得到的液压阻尼器速度响应曲线与试验测得的速度响应曲线进行对比,证明了优化设计结果的有效性[6].
目前粘滞阻尼器的研究多集中于阻尼器减震性能分析、阻尼器结构参数优化和粘滞阻尼器力学模型建立等方向,由于粘滞阻尼器中的介质为非牛顿流体,因而阻尼力随载荷形式和大小变化呈现非线性变化,粘滞阻尼器数学模型中的阻尼系数需要依据试验数据来确定.试验方法虽然能够有效验证理论结果,但增加了研究成本和周期.本文采用AMESim仿真软件,针对孔隙式液压阻尼器的阻尼力进行了理论和仿真研究,并通过试验对仿真结果进行了验证,为粘滞阻尼器非牛顿流体阻尼力的计算提供了有效、快捷的途径.
1 液压隔振系统数学模型
1.1 原理模型
舰船在行驶过程中的颠簸是一个随机振动过程,为保证船载仪器设备的平稳性和安全性,需要安装舰船用隔振系统.隔振系统原理模型如图1所示,该系统主要包括弹性元件、阻尼元件和质量块.为提高隔振效果,采用孔隙式液压粘滞阻尼器,且该液压粘滞阻尼器为速度相关型阻尼器[7].考虑到液压油的压缩性,液压粘滞阻尼器产生的粘滞阻力具有非线性特征[8-10].在建立隔振系统原理模型时,将液压粘滞阻尼器视为由弹簧和阻尼器构成的串联结构[11-12].隔振系统参数如表1所示.
1.2 数学模型
为了研究隔振系统的隔振效果,需要建立隔振系统数学模型.以被隔离设备为研究对象,应用达朗贝尔原理建立隔振系统数学模型.以液压粘滞阻尼器为研究对象,建立液压粘滞阻尼器数学模型,相应模型表达式为
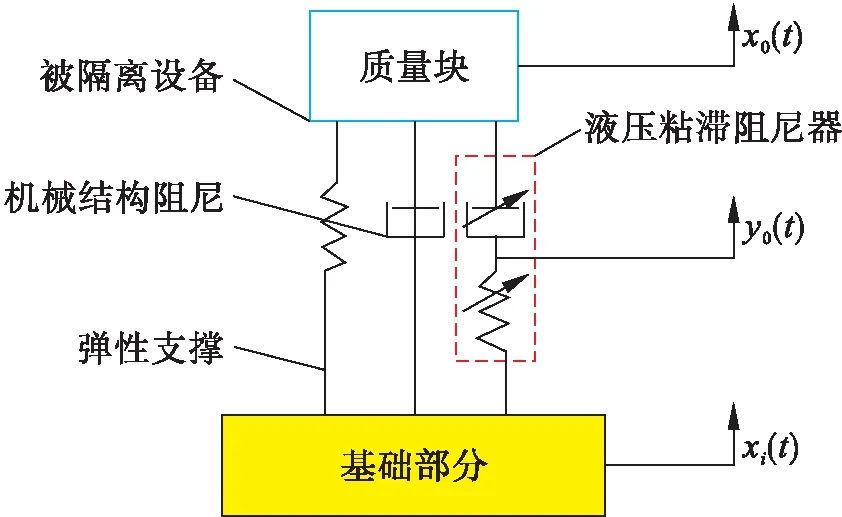
图1 隔振系统原理模型Fig.1 Principle model for vibration isolation system
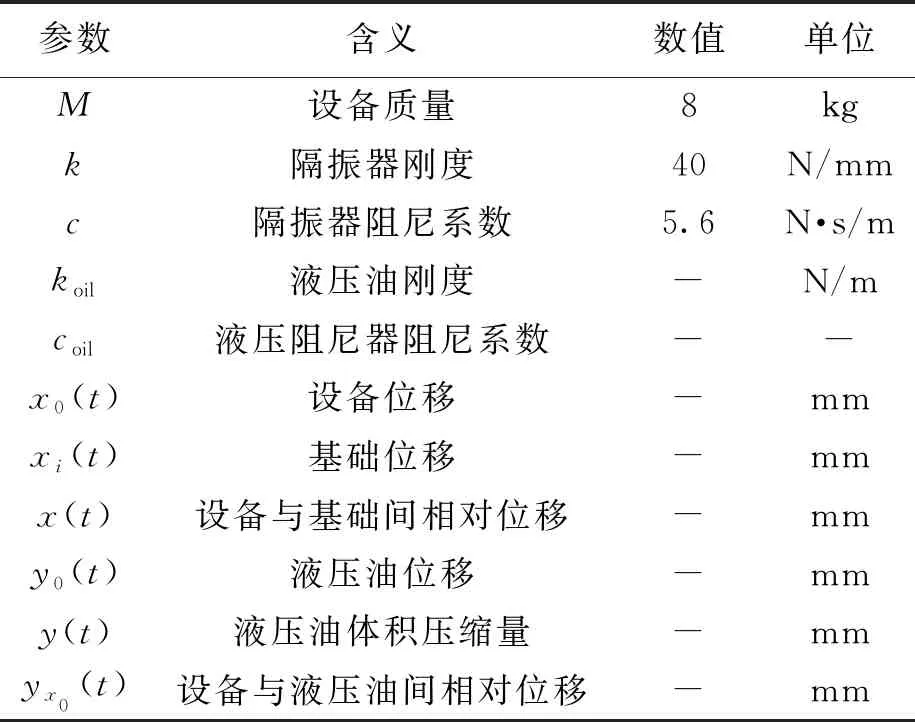
表1 隔振系统参数Tab.1 Parameters of vibration isolation system
(1)
(2)
由于y(t)是一个微小量,可以近似认为yx0(t)≈x(t),修正后的隔振系统数学模型表达式为
(3)
隔振系统的输入为冲击载荷,根据德国军标BV043-85的相关规定,采用图2所示的正负双半正弦波表示水下非接触爆炸冲击载荷,相应冲击载荷参数如表2所示.
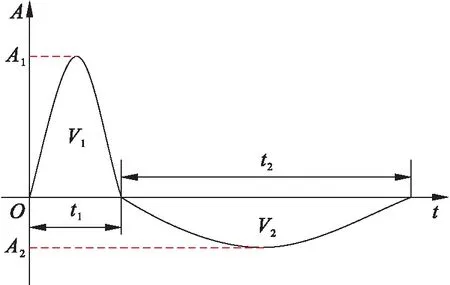
图2 冲击载荷Fig.2 Shock load

表2 冲击载荷参数Tab.2 Parameters of shock load
加载函数表达式为
(4)
式中,f1、f2分别为正、负波频率.
2 液压阻尼力的分析与计算
在上述隔振系统中被隔离设备的质量、机械结构弹性元件的刚度和阻尼元件的阻尼都是已知参量,为了求解式(3)所示的隔振系统数学模型,必须求解液压阻尼器的阻尼力.
2.1 理论计算
液压阻尼力实际上由两部分组成,分别为孔缩效应产生的阻尼力F1与粘滞摩擦阻尼力F2.设阻尼器活塞上开有S组孔径不同的节流孔,且第i组节流孔直径为d1i.设e为阻尼孔总面积,v为阻尼器相对运动速度,则液压阻尼力表达式[13]为
coilv=F1+F2
(5)
(6)
式中:∑ζ为总阻力损失系数(选为0.49),且∑ζ=ζc+ζe,ζc为入口收缩损失系数(选为0.15),ζe为流速扩大损失系数(选为0.34);ck为孔隙系数;α为孔缩衰减系数(0.1≤α≤2),且α=0.103+(e/5)-0.175.
粘滞摩擦阻尼力表达式为
cNvm
(7)
式中:m为流动指数;cN为粘滞阻尼系数.非牛顿流体流动指数是一个小于1的量,由于m值的大小对cN影响不大,因而计算cN时可将m取为1.
液压阻尼力表达式为
coilv=ckvα+cNvm
(8)
由于系统选用的油液为非牛顿流体,液压油的流动指数是一个未知参量,因而无法通过理论计算确定粘滞摩擦阻尼力.本文利用AMEsim软件[14]求解液压阻尼力,确定阻尼力表达式中的流动指数,并完成数学模型的求解和试验验证.
2.2 仿真求解
双出杆液压孔隙式粘滞阻尼器的结构原理如图3所示.该阻尼器主要由活塞杆、端盖、带节流孔的活塞和缸体几部分组成,其主要参数如表3所示.双出杆液压孔隙式粘滞阻尼器的工作原理为:当粘滞阻尼器受到外部冲击时,活塞与液压缸缸体产生相对运动,迫使活塞一侧油液通过节流孔流向另一侧,由孔缩效应产生阻尼力来耗散冲击能量,从而实现隔振的目的.
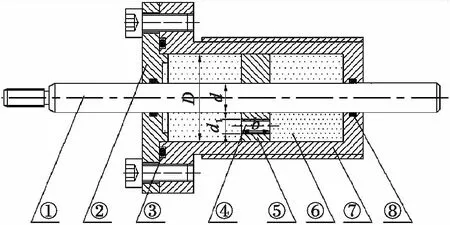
①活塞杆 ②端盖 ③O型密封圈 ④节流孔 ⑤活塞 ⑥阻尼介质 ⑦缸体 ⑧型密封圈图3 双出杆液压孔隙式粘滞阻尼器Fig.3 Double-out rod hydraulic pore-type viscous damper
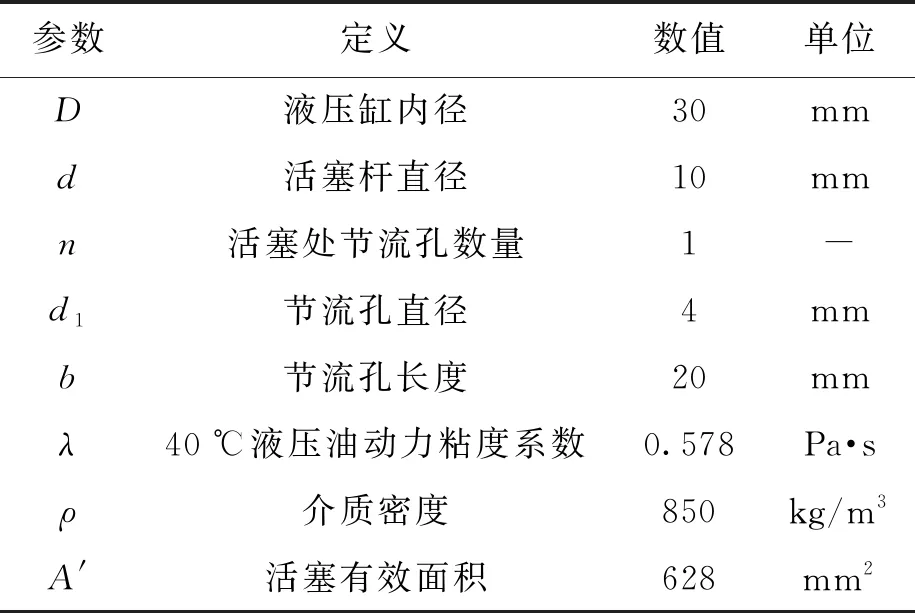
表3 液压阻尼器参数Tab.3 Parameters of hydraulic damper
根据液压隔振器的结构原理、流体力学特性和数学模型分析,分别建立液压阻尼器、隔振弹簧和正负波输入装置的AMESim模型,结果如图4所示.液压限位隔离系统仿真计算模型主要包括信号源、隔离部分、液压限位部分和质量块四部分.
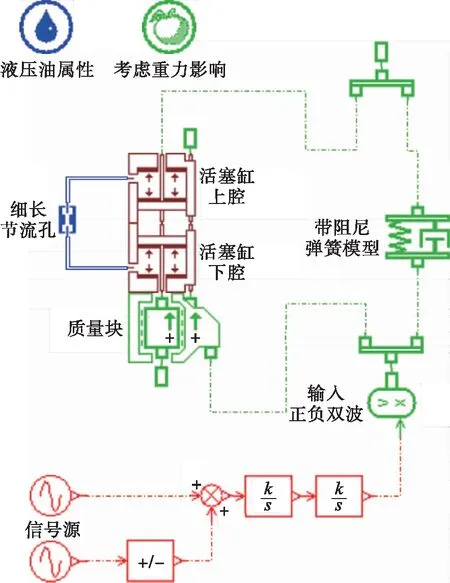
图4 基于AMESim的液压隔离系统仿真模型Fig.4 Simulation model for hydraulic vibration isolation system based on AMESim
在AMESim模型中施加式(4)所示的载荷,得到液压缸上、下腔压力,当输入载荷(加速度峰值)A1为40g,A2为18.824g时,液压缸上、下腔压力如图5所示.液压缸上、下腔压力差与活塞有效面积的乘积即为液压阻尼器的阻尼力值[15],即
ΔpA′=ckvα+cNvm
(9)
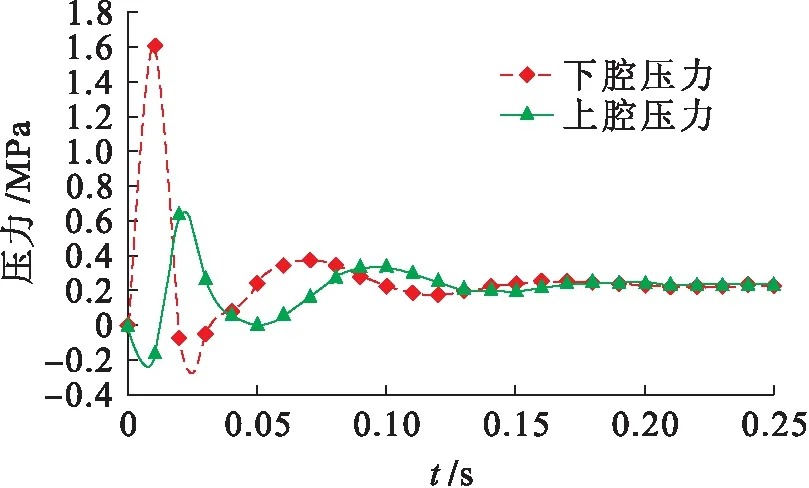
图5 液压缸上、下腔的压力Fig.5 Pressure of upper and lower chambers of hydraulic cylinder
由式(9)求出流动指数,得到其平均值为0.838 6,将其代入式(8)中进行计算.将通过AMESim仿真得到的液压阻尼器阻尼力ΔpA′与由式(8)计算得到的阻尼力coilv进行比较,结果如图6所示.由图6可见,阻尼力ΔpA′与coilv趋势非常接近,最大峰值误差为4.6%.
为了探究阻尼器结构参数对系统性能的影响,对阻尼孔尺寸与阻尼力的关系进行了仿真分析,将AMESim模型中阻尼孔的直径分别设定为2、3、4、5和6 mm,施加同样载荷得到图7所示的阻尼力.
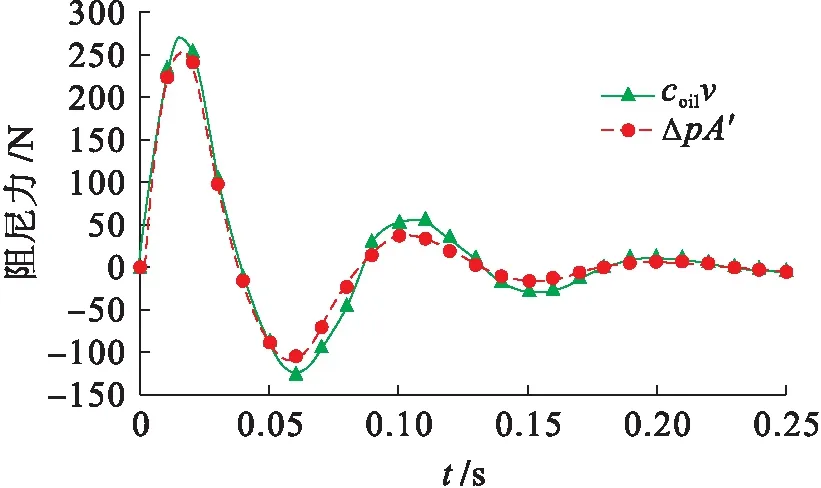
图6 阻尼力与比较Fig.6 Comparison between damping forces
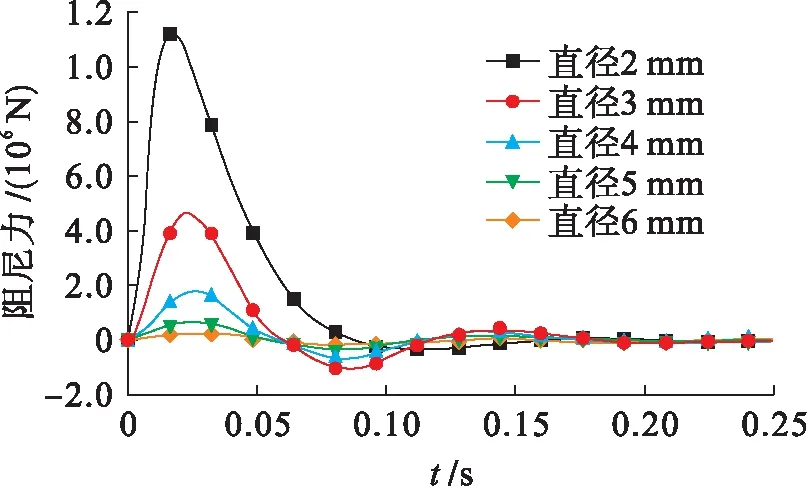
图7 阻尼孔直径为2~6 mm时的阻尼力Fig.7 Damping force of damping holes with diameter from 2 mm to 6 mm
由图7可见,阻尼孔越小产生的阻尼力越大,当阻尼孔直径为2 mm时,产生的阻尼力最大.当阻尼孔直径从2 mm增大到3 mm时,对应的阻尼力峰值迅速减小,此过程变化较为剧烈.在实际工程中需要根据隔振系统整体性能指标来选取阻尼孔直径的尺寸.
3 液压阻尼力的试验验证
3.1 试验装置与原理
为了验证基于AMEsim仿真结果修定的隔振系统数学模型的正确性,设计隔振系统的试验装置如图8所示.该试验装置由底座、隔离部分、被隔离设备和液压阻尼器四部分构成,液压阻尼器的缸筒通过法兰盘与隔振系统的底座刚性连接,由液压阻尼器中带冲击头的活塞杆支撑被隔离设备.图9为垂向双波冲击台原理简图.采用500 kg垂向双波冲击试验机进行冲击试验,该试验机主要由基础系统、液压系统、机械系统和测控系统等几部分组成[16],其主要工作原理为:冲击前由蓄能器存储冲击所需能量,冲击时蓄能器中的能量在正波液压系统控制下释放,驱动冲击锤撞击冲击台产生正波冲击;当冲击台向上运动达到最大速度时,阻尼缸在负波液压系统控制下对冲击台实施制动产生负波冲击,使冲击台减速运动直到停止.

图8 双出杆孔隙式液压阻尼器试验装置Fig.8 Test device of double-out rod hydraulic pore-type viscous damper
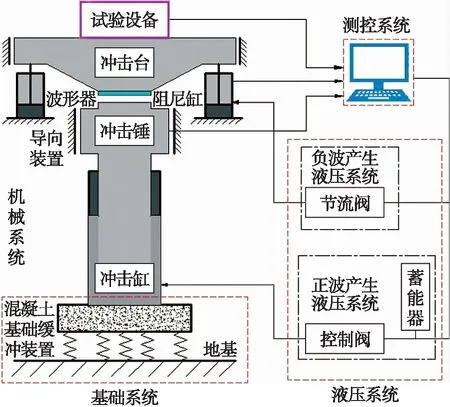
图9 垂向双波冲击台原理简图Fig.9 Schematic principle diagram of vertical double wave shock table
调整试验装置各部分参数使其同仿真计算参数一致,通过垂向双波冲击试验机施加与仿真相同的冲击激励进行冲击试验验证.
3.2 冲击试验与仿真数据对比
图10、11为当冲击试验机施加特定冲击激励(参数见表1)时,液压隔振系统加速度响应和相对位移响应的仿真计算与试验结果时域历程对比曲线.不同冲击载荷激励下,液压隔振系统的相对位移响应和加速度响应试验峰值数据与仿真计算误差如表4所示.
结合图10、11和表4可知,在40g输入载荷作用下试验测得的系统加速度响应峰值为20.67g,仿真计算误差为2.5%;试验测得的系统相对位移响应峰值为13.11 mm,仿真计算误差为2.97%,均在误差允许范围内.可见,液压隔振系统通过试验得到的相对位移响应和加速度响应时域历程曲线与仿真计算结果具有较好的一致性.由表4可知,在40g~70g输入载荷作用下系统的相对位移响应和加速度响应峰值随冲击载荷的变化趋势与仿真计算具有较好的一致性,仿真计算与试验结果的最大误差为5.48%,远远小于20%的允许误差范围,证实了本文数学模型的准确性.
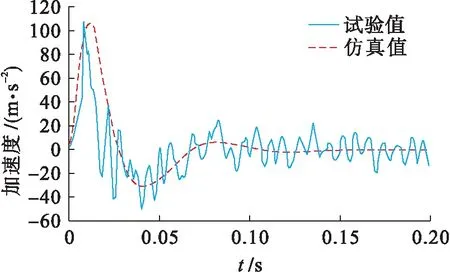
图10 系统加速度响应对比Fig.10 Comparison of acceleration response of system
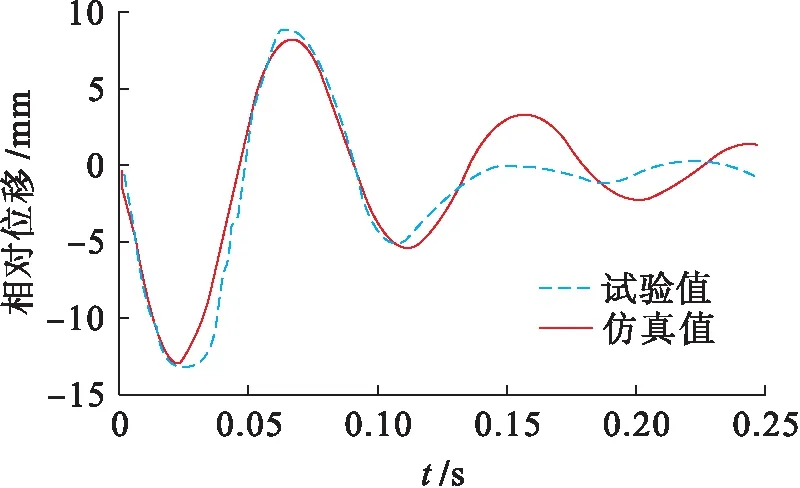
图11 系统相对位移响应对比Fig.11 Comparison of relative displacement response of system
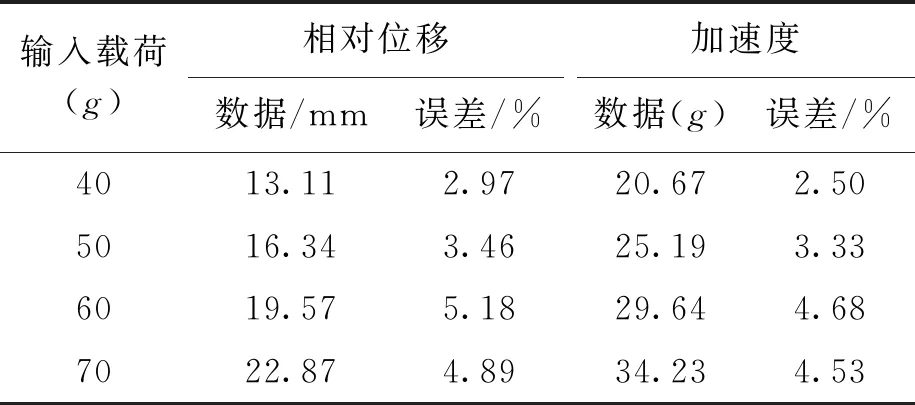
表4 不同载荷下隔振系统冲击响应数据Tab.4 Shock response data of vibration isolation system under different loads
4 结 论
通过以上分析可以得出如下结论:
1) 孔隙式液压隔振系统数学模型的建立过程中考虑了液压阻尼力的非线性特征,提出了利用AMESim软件仿真计算液压阻尼器阻尼力的有效方法,并确定了数学模型中的流动指数;
2) 基于AMESim软件计算液压阻尼器阻尼力的方法相比常规试验法节约了成本,缩短了液压隔振器的开发周期;
3) 利用MATLAB软件对液压隔振系统的数学模型进行了仿真计算,其结果与试验数据相比具有较好的一致性,仿真计算误差均在允许范围内,表明本文建立的隔振系统数学模型能够准确反映隔振系统各参数特性.
综上所述,在设计舰载设备用液压隔振装置时,通过AMESim软件仿真来确定液压阻尼器阻尼力的方法是切实可行的,能够在仿真基础上对试验做出较为准确的预测.这种方法为液压隔振系统的理论研究提供了行之有效的理论依据.
