参考坐标系对Davis-Smith 方法计算磁通门磁强计磁零点补偿值的影响

王国强，程甚男‡，孟立飞，易 忠，肖 琦，潘宗浩，胡小文，刘 凯，张铁龙,4

（1.哈尔滨工业大学（深圳）空间科学与应用技术研究院，深圳518055；2.北京卫星环境工程研究所，北京100094；3.中国科学技术大学 地球和空间科学学院，合肥 230026；4.奥地利科学院 空间研究所，格拉茨A-8042）

0 引言

卫星通过搭载科学载荷设备记录空间环境中的物理参数，从而为开展空间探索提供科学数据[1-2]。因此，科学载荷技术的研发对空间科学的发展具有重要意义。磁场测量是空间探测中的一项重要任务[3-6]，精确的磁场测量有助于研究磁重联、波粒相互作用等物理过程及一些空间小尺度的物理结构等[7-11]。搭载在卫星上的磁测设备一般为磁通门磁强计，其所测得的磁场包含卫星本体磁场、磁强计磁零点补偿值（简称零位补偿）和自然磁场[2-3]。为获得准确的自然磁场，需要明确磁强计的零位补偿。尽管在卫星发射之前会对磁通门磁强计进行地面标定，但零位补偿值会随时间发生缓慢变化[12-14]。因此，需要对磁通门磁强计进行在轨标定，从而获得可靠的零位补偿值。

对空间探测的磁通门磁强计进行在轨标定的常用技术为Davis-Smith 方法[15-17]。空间等离子体环境存在大量磁流体力学波动，包括阿尔芬波动和压缩波动，其中阿尔芬波动不会改变总磁场强度[18-20]。基于阿尔芬波动对应的磁场三分量与总磁场强度不相关这一特征，利用Davis-Smith 方程可获得准确的磁强计零位补偿值[16]。然而，行星际空间中没有纯粹的阿尔芬波动，即磁场扰动中存在压缩波动[16]，因此利用Davis-Smith 方程计算出来的零位补偿值不可避免地存在计算误差，但可以通过筛选出阿尔芬特性足够强的磁场波动来确保磁补偿的计算误差足够小。为此，有学者提出复杂的磁场波动筛选判据[16]，并已应用于美国MMS（Magnetospheric Multiscale）卫星的磁通门磁强计在轨标定[21]。

近期的数值分析结果表明，无论是阿尔芬波动还是压缩波动，其波动参数（如波动幅度、周期等）对Davis-Smith 方程计算磁强计的零位补偿值存在不同程度的影响[22-24]——压缩波动幅度越小，零位补偿值的误差则趋向于更小[22]；而当压缩波动周期与阿尔芬波动周期相同时，即便压缩波动幅度较小，Davis-Smith 方程的计算结果也可能出现非常大的误差[23]；零位补偿值的误差在压缩波动所在的磁场分量上会相对较大，这表明同一波动在不同参考坐标系中对Davis-Smith 方程的计算误差影响可能不相同[22]。

本文利用数值分析，研究不同直角坐标系中Davis-Smith 方程对同一磁场波动的计算误差特征，以考查参考坐标系对基于Davis-Smith 方法的磁通门磁强计在轨标定的影响。

1 Davis-Smith方程

设磁通门磁强计所测磁场为BM=(Bx,By,Bz)，零位补偿值为O=(Ox,Oy,Oz)。假定磁强计所测到的卫星本体磁场噪声为0（该假设在卫星上放置磁传感器的伸杆足够长的情况下是合理的），则自然磁场BA=BM–O。如果卫星上的磁通门磁强计探测到一段纯的阿尔芬波动，则将该时段的磁场数据BM代入Davis-Smith 方程，即可获得零位补偿值O。Davis-Smith 方程的表达式[16]为

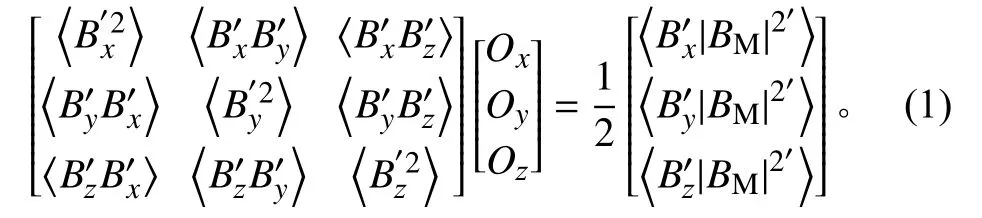
其中Bx′、By′、Bz′和|BM|2′分别为Bx、By、Bz和|BM|2与其各自的平均值之差。

2 数值仿真

假设卫星本体磁场为0且磁通门磁强计不存在磁零点漂移，即零位补偿值为0，那么磁强计所测得磁场BM即为自然磁场BA。此时，将BM代入Davis-Smith 方程后所得到的零位补偿值O即为该方程的计算误差。我们首先设定初始平面波动，然后通过旋转坐标系来考查该波动在不同参考坐标系下Davis-Smith 方程的计算误差分布特征。

2.1 初始波动设置

为便于分析，我们假设阿尔芬波动为单色平面波动，扰动分量分别在x和y方向上；压缩波动只在z分量上。该设置类似于磁场矢量所在的坐标系为场向坐标系，磁场三分量设置如下：

式(2)～式(4)中：A、C分别为阿尔芬波动和压缩波动的幅度；ωA和ωC分别为阿尔芬波动和压缩波动的角频率。磁场单位为nT。

采用式(2)～式(4)设置2个波动事件，如图1所示。事件1的阿尔芬波动幅度A=1 nT，周期为60 s；压缩波动幅度C=0.2 nT，周期为10 s。事件2的阿尔芬波动幅度A=2 nT，周期为90 s；压缩波动幅度C=0.3 nT，周期为20 s。在后文分析中，这2个波动的时间窗口分别取对应阿尔芬波动周期的10倍时长。

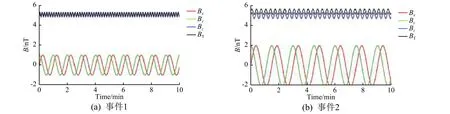
图1 所设置波动事件的磁场三分量和总磁场Fig.1 Three components of the magnetic field and the strength of the two wave events designed in this paper

2.2 坐标系旋转对单个波动事件的零位补偿误差的影响

对磁场矢量按如下方式进行坐标系转换：将xyz坐标系的磁场矢量先绕y轴旋转一个角度φ，得到新坐标系x′y′z′；再将x′y′z′坐标系下的磁场矢量绕z′轴旋转θ角，从而得到x″y″z″坐标系下的磁场数据。把x″y″z″坐标系下的磁场数据代入Davis-Smith 方程，就可以考查坐标系对零位补偿计算的误差特征。θ按步长1°从0°增加到360°；φ按步长1°从0°增加到180°。每进行一次坐标系转换，便将x″y″z″坐标系下的磁场数据代入到式(1)计算出对应的零位补偿值。

图2展示了波动事件1对应的磁通门磁强计零位补偿值O随θ和φ的分布。这里需要注意的是，图中所示的零位补偿值为Davis-Smith 方程的计算误差。如图2(a)所示，Ox、Oy和Oz的绝对值随θ和φ的变化在0.01～10 nT之间变化：Ox在(θ,φ)=(0°,90°)或(180°,90°)附近达到极大值；而Oy在(θ,φ)=(90°,90°)或(270°,90°)附近达到极大值。Ox和Oy随θ的变化相差90°可能与Bx和By的相位相差90°有关。Ox、Oy在φ=0°和180°时达到极小值；而Oz在φ=0°和180°时达到极大值，在φ=90°时达到极小值。图2(b)展示了Ox、Oy和Oz的正负符号：Ox在0°＜θ＜90°和270°＜θ＜360°区间为负，在90°＜θ＜270°区间为正；Oy和Oz也在不同的θ或φ区间表现出不同的正负情况。由此可见，即便是同一波动，参考坐标系对Davis-Smith 方程所计算零位补偿的精确度亦有显著影响。

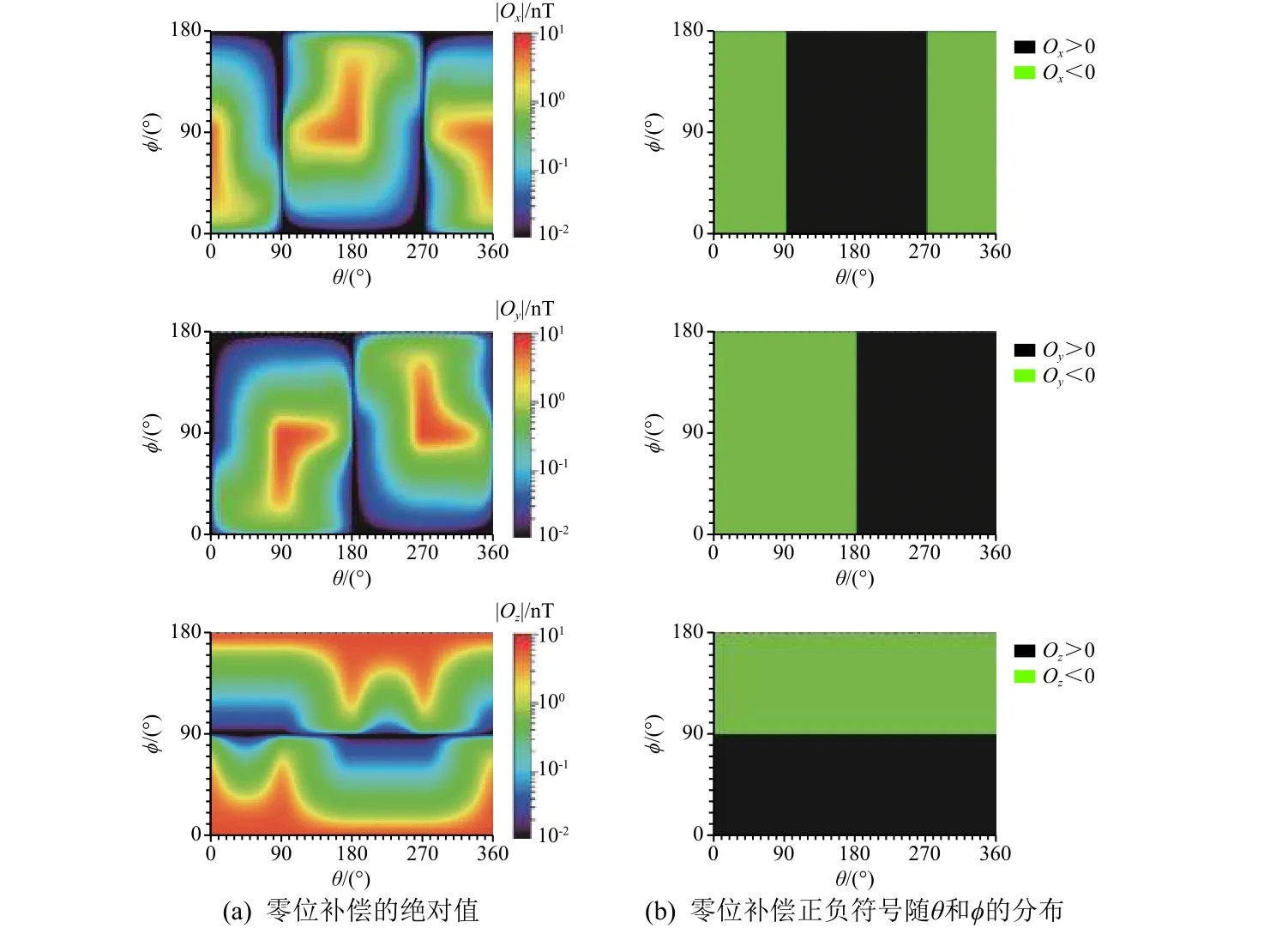
图2 波动事件1的零位补偿的绝对值及其正负符号随θ 和φ的分布Fig.2 Theabsolutevalue (left)and the plusor minus (right)of the magnetic zero-offset for wave event I

近期的数值分析结果表明，磁场压缩波动若与阿尔芬波动周期相同，则即便压缩波动幅度较小也可能产生较大的零位补偿计算误差[21-22]。将波动事件1中的压缩波动周期改为与阿尔芬波动周期相同，即60 s，其他参数保持不变，然后分析参考坐标系对该波动的影响（如图3所示）。可以发现，图3中磁场三分量的零位补偿误差与图2显著不同（图中白色区域表示在计算零位补偿时，求解逆矩阵的结果不可信，从而导致零位补偿的计算值不可靠）：Ox和Oy在φ=80°以及90°＜θ＜180°和270°＜θ＜360°区间出现极大值，误差可达几十nT，远大于阿尔芬波动的幅度（1 nT）；在0＜θ＜90°和0＜φ＜80°以及180°＜θ＜270°和80°＜φ＜160°区间，Ox和Oy的值非常小（在0.01 nT 附近或更小）；Oz在φ=170°附近出现极大值。对比图3和图2可以发现，即便是同一阿尔芬波动，压缩波动周期是否与阿尔芬波动周期相同亦对Davis-Smith 方程计算结果的精确度有显著影响。

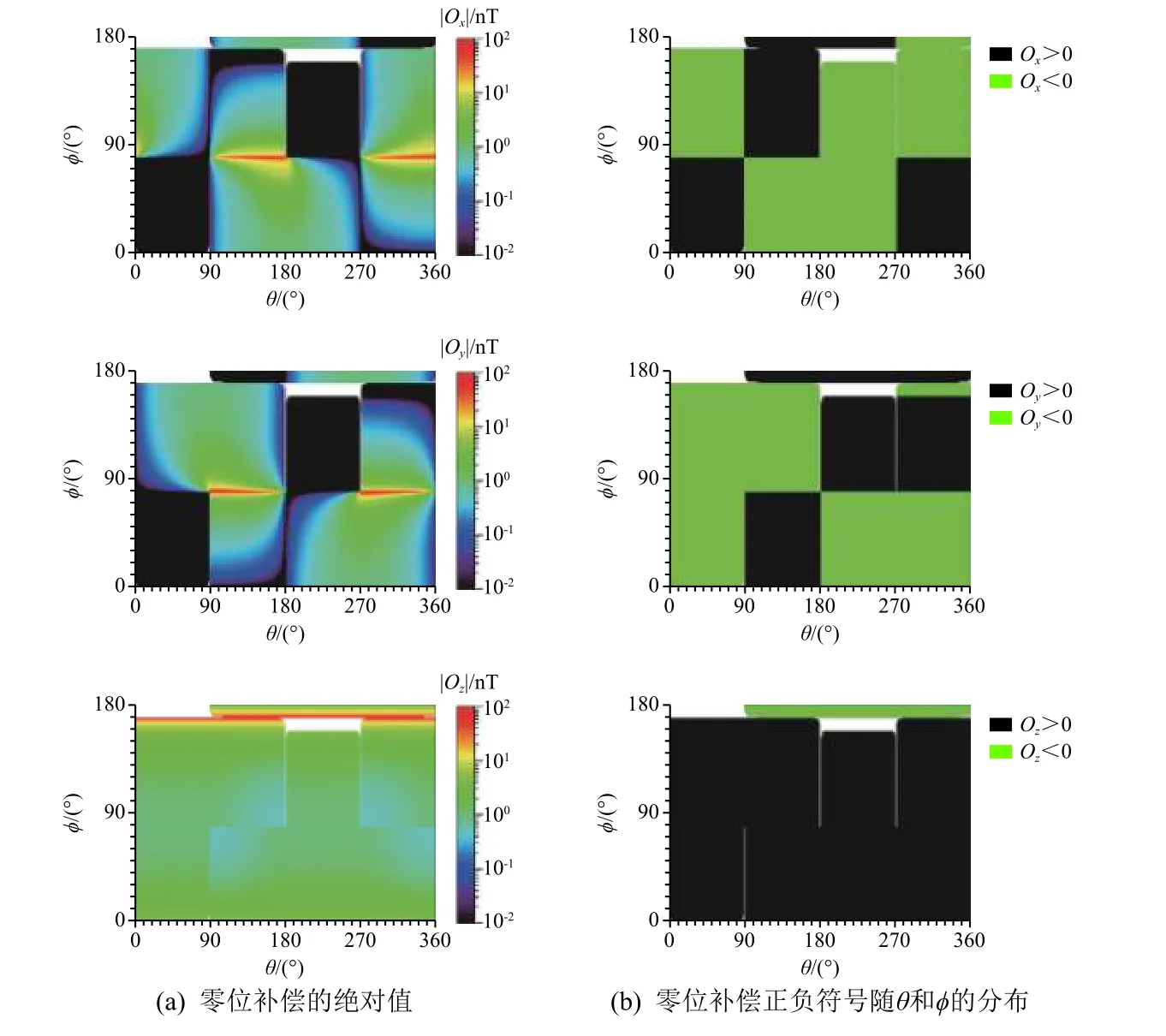
图3 波动事件1的零位补偿的绝对值及其正负符号随θ 和φ的分布（其中该事件中的压缩波动周期已修改为与阿尔芬波动周期相同）Fig.3 The absolute value(left)and the plus or minus(right)of the magnetic zero-offset for wave event I,in which the period of the compressional wave is set to be the same with the Alfvén wave

图4所示为波动事件1对应的零位补偿总误差OT，其中图4(a)对应波动事件1中压缩波动周期为10 s，图4(b)中的压缩波动周期与阿尔芬波动周期相同，为60 s。图4(a)显示：OT最小可低至0.4 nT，最大可达5 nT；在θ=45°、φ=130°或θ=225°、φ=50°附近，OT达到极小值。这表明，在对单个波动用Davis-Smith 方程进行计算时，挑选合适的磁场波动可显著减小OT的计算误差。图4(b)显示：OT在φ=80°以及90°＜θ＜180°和270°＜θ＜360°区间，或φ=170°时，误差可达几十nT；OT的最小值在1 nT附近。对比图4(a)和图4(b)可以发现，当压缩波动周期与阿尔芬波动周期不同时，OT值会显著变小。因此，在对磁通门磁强计进行在轨标定时，如果阿尔芬波动事件足够多，应尽可能选取与压缩波动周期不相同的波动事件来用Davis-Smith 方程计算零位补偿。

图4 波动事件1的零位补偿总误差Fig.4 The total error of the magnetic zero-offset calculated by using the data from waveevent I

2.3 坐标系旋转对波动事件零位补偿误差的影响

在对磁通门磁强计进行在轨标定时，一般选取若干个阿尔芬特性足够强的时段来用Davis-Smith方程计算零位补偿。同时将波动事件1、2的数据代入Davis-Smith 方程来计算零位补偿，且为考查参考坐标系对计算结果的影响，假设波动事件1的磁场数据保持不变，然后对波动事件2进行坐标系旋转。图5给出了OT随θ和φ的分布，其中图5(a)中压缩波动周期分别为10 s和20 s，图5(b)中压缩波动周期与对应的阿尔芬波动周期相同。图5(a)中OT在0.1～5 nT 区间变化，这表明尽管用于计算零位补偿的2个波动事件的阿尔芬特性足够强，其误差依然可能非常显著。在给定θ时，OT随φ增大而减小，因此选取合适参考坐标系（相对于场向坐标系而言）下的波动事件，零位补偿值的精度可以得到显著提高。和图4(a)对比可以发现，用2个波动事件的磁场数据来计算零位补偿的误差一般而言比用单个波动的要小。

图5 用2个波动事件计算的零位补偿总误差Fig.5 The total error of the magnetic zero-offset calculated by using the data from two wave events

图5(a)中的OT值从整体而言比图5(b)中的要显著减小；但在θ=270°和φ=45°附近，图5(b)中的OT值比图5(a)中的小，约为0.3 nT。由此可见，在选取阿尔芬特性强的波动时段时，不仅需要考虑压缩波动周期，还需要考虑参考坐标系（或阿尔芬波动的波矢方向）的影响。

3 结束语

本文通过数值仿真研究了参考坐标系对用Davis-Smith 方程计算磁通门磁强计零位补偿的影响。结果发现：即便是同一个磁场波动事件，在不同的参考坐标系下通过Davis-Smith 方程计算产生的误差也是不同的，其最大误差与最小误差之间相差可达1个数量级或者更大；当用2个波动事件来计算零位补偿时，即便是相同的2 个波动，计算结果也会随着其中1个波动扰动平面的不同而不同，其误差也可达到不容忽视的程度。尽管如此，利用2个波动事件来计算零位补偿，其误差相比于单个波动事件而言显著减小。以上仿真结果表明，在挑选阿尔芬特性足够强的波动时段时，还需充分考虑参考坐标系的影响，以有效降低Davis-Smith 方程的计算误差。