正弦扫频振动试验结构响应的高精度频谱分析方法

王营营，白 杨，徐晓辉，王继虎，李霖圣

（1.上海卫星装备研究所，上海200240；2.上海航天技术研究院，上海201109）

0 引言

正弦扫频振动试验是航天器研制过程中常开展的力学环境模拟试验，其试验结果对于评估航天器耐受振动环境的能力、改进航天器在轨可靠性设计等起着重要作用。

力学环境试验数据采集和分析处理系统具有对应试验时间短、测量通道多、数据流量大、实时性要求高、可靠性要求高等特点。由于单套数据采集系统的通道数发展受到硬件性能的限制，以分布集成式系统代替超大系统模式成为多通道大型数据采集系统的发展趋势[1]，而大量分布式采集和存储的结构响应时域数据对数据后处理能力提出了较高要求。

航天器上安装的力学环境测量系统可以测量真实的主动段动力学环境和在轨微振动力学环境，对航天器的力学环境优化和设计有重要参考价值[2]。地面振动试验期间进行测试，并和地面数据采集系统得到的幅值谱进行对比分析，可以验证在轨力学环境测量系统的有效性[3]。由于在轨力学环境测量系统在航天器上独立工作，和地面振动控制仪不能实现同步，对其采集的时域振动响应数据进行准确的频谱分析才能实现数据对比和开展系统有效性研究。

地面振动试验数据采集系统通常利用振动控制仪输出的COLA（constant output level adapter）信号进行实时频率辨识，从而实现同步数据采集和在线数据处理。实时处理振动响应数据对系统硬件要求高，而系统的通道数发展受到硬件制约，因此不依赖COLA 信号的正弦振动试验时域数据分析方法在结构响应分析中有重大研究意义。

有效的正弦振动响应信号分析基于对适用于非平稳信号的时频分析方法的探索。短时傅里叶变换（STFT）定义的谱图是简单、直观的时频表示，但其受到测不准原理的制约，不能同时兼顾时间分辨率和频率分辨率[4]。使用离散傅里叶变换（discrete Fourier transform,DFT）分析振动响应信号时，时域信号的整周期截断和同步采样通常难以实现，频谱泄漏会造成严重的分析误差[5]。一般利用窗函数和插值方法来减少频谱泄漏[6]，通过调整窗宽和采样率等技术可以在一定程度上减小误差[7]，但是窗函数的引入会对幅值分析的精度产生影响[8]。针对DFT方法中非同步采样信号的幅值和频率分析精度不高的问题[9]，对泄漏频谱进行插值校正[10]或推导出真实频谱[11]都可以达到减小误差的效果。针对信号的非整周期截断问题，采用残周期正弦拟合方法[12]可以获取低频信号的振动参数。基于Hilbert 变换和滤波算法可以利用驱动信号[13]或构造参考信号[14]分析得到频谱曲线，但是滤波处理的精度和结构特性有关，并且分段滤波会导致局部的幅值误差较大。单帧FFT 法[15]可以有效识别结构动特性和频响曲线，但是无法得到准确的幅值谱。基于自适应带通滤波的STFT方法[16]能有效改善STFT幅值分析的精度，但与地面数据采集系统的处理结果相比有较大误差。

本文针对不依赖COLA 信号的正弦振动响应分析，提出一种基于扫频规律的频率跟踪DFT 方法，根据正弦扫频试验的频率变化特性[17]，基于过零点检测和最小二乘法进行信号频率辨识，同时在较小的时间尺度上将正弦扫频信号近似为平稳周期信号，根据基频对时域振动响应信号进行整周期截断和DFT频谱分析，旨在提高正弦振动响应频率和幅值的分析精度。

1 时频分析理论

1.1 正弦扫频振动试验概述

正弦扫频振动试验是按照规定的振动量级，在一定频率范围内连续改变振动频率来激励试验件。其振动频率的变化率称为扫描速率。

试验激振频率f、试验时间t和扫描速率β的关系在线性扫频中表示为

在对数扫频中表示为

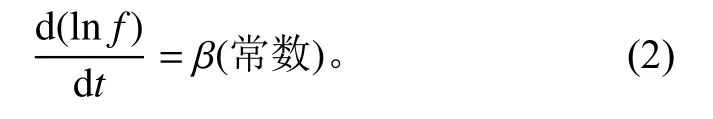
将振动试验的起始频率记为f0，起始时间记为t0，利用式(2)可得到对数扫频试验的实时频率f和时间t的关系为

若取β=k×ln 2，则可得到工程中常用的倍频程表示形式

式中k为倍频程扫描速率。

激振频率f与时间t在线性扫频和对数扫频试验中均有比较简单的函数关系，对于复杂的频率扫描方法，可以用曲线函数、分段函数或者离散点序列等方式来描述。正弦扫频试验中的频率扫描规律是已知的，只有起始时间t0是由数据采集器定义的，只需确定t0就能按照频率扫描规律计算出任意时刻的激振频率。

1.2 频谱分析方法

正弦振动试验地面数据采集系统通过COLA信号得到振动台的实时激振频率，系统硬件以高采样率进行时域数据采集、实时分析处理、数据传输和存储。振动响应幅值谱的计算方法主要有绝对峰值法、平均值峰值法、有效值峰值法和滤波方式峰值法。除绝对峰值法外，其他3种方法都有一定的滤波效果；滤波方式峰值法的分析速度快，处理结果曲线平滑，并且可以获得相位信息，是工程中常用的分析方法。

滤波方式峰值法将正弦振动信号表示为

式中：N为数据块中的数据个数；Δt为采样周期。

地面数据采集系统的硬件采样率通常远高于信号基频：以比利时LMS公司的SCADASⅢ系统为例，其前端单通道采样率可达到204.8 kHz，而振动试验频率上限一般小于2 kHz。系统在1个信号周期内即可采集到足够的数据，然后通过最小二乘法和式(7)得到ac和as的精确估计值，从而计算出信号幅值A(ω1)。

使用振动响应时域数据后处理的方法进行频谱分析主要有2个难点：1）通常没有COLA 信号作为参考，难以进行精确的频率辨识；2）受时域数据传输和存储过程的硬件性能限制，实际的采样率较低，通过式(7)进行幅值估计时，分析结果的抗干扰能力较差。

2 频率跟踪DFT方法

2.1 正弦扫频信号的频率识别

通常正弦振动试验激励频率和结构响应频率的相关性很高，因此，由过零点检测方法得到的数据点(tr,lnfr)应该落在式(8)所描述的直线附近。如图1所示，对过零点检测法计算出的数据点序列使用最小二乘法即可得到lnf和时间t的直线表达式；利用式(8)和起始频率f0可得到起始时间t0，然后根据式(4)进行频谱分析中的频率辨识。

对于试验频率单调递增或单调递减的扫频方式，只需要1对精确的时间‒频率值就能计算出起始时间t0，但考虑由过零点检测方法得到的频率值容易受到干扰信号影响，故需要取响应信号的多个过零点检测值并利用最小二乘法减小分析误差。试验频率不符合单调递增或单调递减规律时，可以先估计起始时间t0的大致范围，使得t0的取值范围小于试验频率的变化周期。

结构的固有频率特性和信号干扰对过零点检测方法的频率计算精度影响较大，一般可以通过滤波和设置阈值的方法排除数据畸变点。受到非同步采样的影响，在采样率较低时，高频信号的频率计算误差也比较大，在最小二乘法中只选取低频段的数据点可有效减小误差，提高频率辨识精度。

2.2 频率识别算例

对于二次函数扫频正弦振动，瞬时频率fi(t)是时间t的二次函数。例如，式

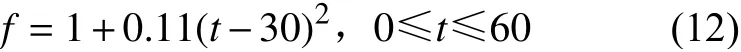
的含义为：0 s—30 s的时间内，瞬时频率从100 Hz按照二次函数规律连续变化到1 Hz；在30 s—60 s的时间内，再从1 Hz 连续变化到100 Hz。

利用式(12)的扫频规律可以构造加速度幅值为1g的扫频数据。为模拟数据采集器时间和扫频时间不能同步的情况，在时域扫频数据前后分别增加5 s 的定频振动（加速度幅值1g、频率100 Hz）。将扫频起始时间记为t0，显然在扫频数据前面增加了5 s的定频数据后，有t0=5。在式(12)中引入起始时间t0，将其改写为

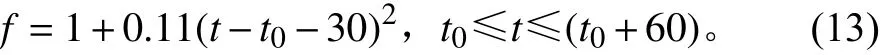
下面假设t0是未知量，并使用过零点检测法和最小二乘法对构造的时域扫频数据进行分析，来详细说明求解t0的过程。在开始求解t0之前，将图2所示的冲击响应信号叠加到时域扫频数据中，为过零点检测方法引入干扰项，最终得到的时域扫频数据见图3，时间长度70 s，STFT得到的频谱如图4 所示。

第1步，在时域数据中每隔2 s（分别从时刻0 s、2 s、4 s、 ···、68 s开始）使用过零点检测方法按照式(9)向后寻找2个过零点，2个过零点时间差的倒数为频率值fi，2个过零点时刻的平均值为时刻ti。在70 s的扫频数据总时长中，可以计算得到35组时间‒频率值(ti,fi)，其中1≤i≤35。

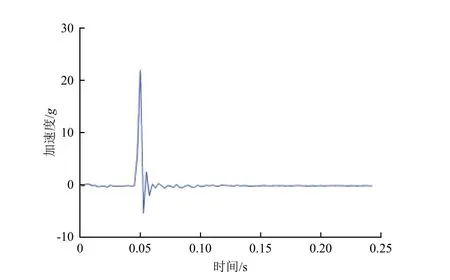
图2 冲击响应信号Fig.2 Shock response signal

图3 二次函数扫频振动时域响应Fig.3 The time domain response of quadratic sine-swept vibration

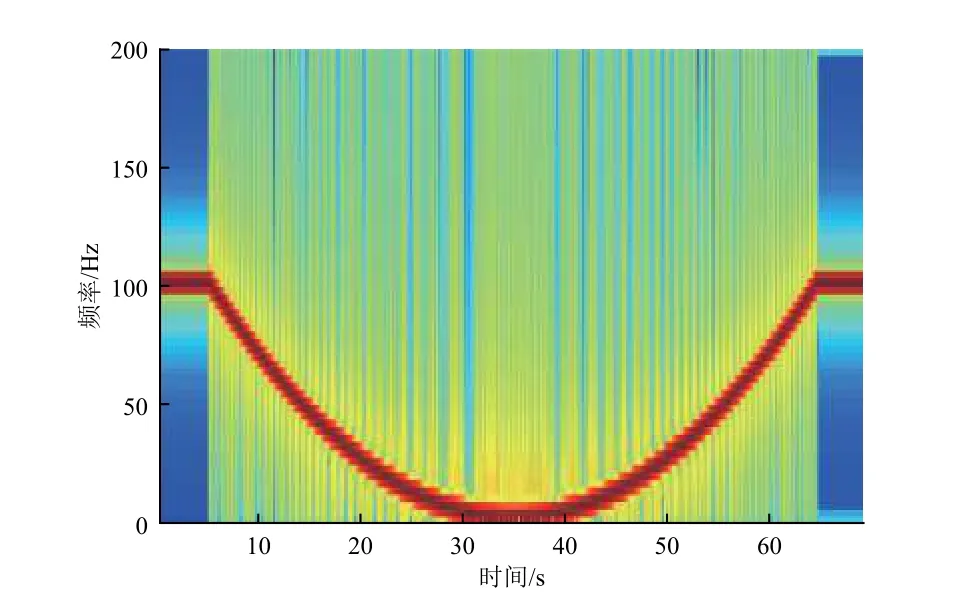
图4 二次函数扫频振动频谱Fig.4 The spectrum of quadratic sine-swept vibration

第2步，选取低频数据计算均方根误差。由于低频部分每个信号周期内的采样点数目较多，过零点分析所得频率值fi的误差小，所以优先使用低频数据。本文取1≤f≤5，根据式(13)可得ti需要满足条件：由于0≤t≤70，根据式(13)可得起始时间t0可能的取值范围为[0,10]，在该范围内取t0为任意值，通过式(14)即可选取出[ta,tb]范围内的过零点分析值(ti,fi)，其中m≤i≤n。图5所示为：t0=1的情况下m=14、n=18；图6所示为：t0=9的情况下m=18、n=23。

图5 瞬时频率曲线（t0=1 s）Fig.5 Thecurve of instantaneousfrequency (t0=1 s)

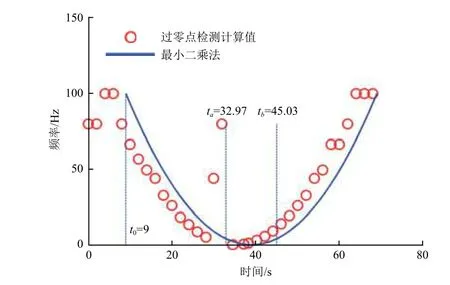
图6 瞬时频率曲线（t0=9 s）Fig.6 Thecurve of instantaneousfrequency (t0=9 s)

的过零点分析值(ti,fi)剔除；将区间[ta,tb]内剩余的N个过零点分析值记为(tj,fj)，其中1≤j≤N，重新计算均方根误差

对于任意的t0值，均可按照上述方法计算出相应的均方根误差ERMS。

利用最小二乘法的原理，求解t0最优解的问题可以描述为：在[0,10]范围内求t0的值，使得均方根误差ERMS的值最小。求解该问题最直接的方法是在[0,10]范围内以采样周期为步长求解所有ERMS，通过寻找ERMS的最小值来确定对应的t0。该问题也可以使用工程数值优化算法快速求得最优解（如图7所示），其值为t0=5。

图7 最小二乘法计算结果Fig.7 The resultsof least squaresmethod

2.3 时频分析方法

利用式(21)可得到ac和as的值，再根据式(6)即可得到该频率处的信号幅值。该方法和滤波方式峰值法相似，在计算幅值的同时可获取相位信息。

上述方法基于响应信号的频率辨识和频率跟踪，并使用整周期截断有效减小了DFT频谱分析误差。由于数据截断时将信号频率视为常数，所以频率变化太快或数据长度N较大时会产生截断误差。另一方面，由于信号的非同步采样导致谱线频率fk不会精确等于信号基频，所以采样频率相对信号基频太小或数据长度N较小时会增大频谱分析误差。航天器正弦振动试验中，为了激发结构在试验频率的稳态响应，扫描速率通常不宜太快，取周期数M=4可以有效地控制误差。

3 对比分析及验证

3.1 与构造的正弦扫频试验数据幅值谱理论值的对比

算法构造一个正弦扫频数据序列，使用频率跟踪DFT 方法进行时频分析，并将计算结果和理论值进行对比，验证第2章所述方法的计算精度。

构造正弦扫频试验数据，其采样率为1000 Hz，频率范围1～200 Hz，扫描速率4 oct/min，加速度幅值1g。用频率跟踪DFT 方法进行时频分析：频率范围2～100 Hz，频率分辨率为每倍频程100谱线。对构造的时域数据进行过零点检测并选取2～5 Hz 的频率范围进行频率识别，频域幅值谱的理论值和分析结果的曲线见图8，具体结果对比和误差数据见表1。

由图8可见，幅值谱的高频部分误差稍大，这主要是因为采样频率相对高频段信号的基频较小，导致频谱分析中非同步采样误差的影响较大。由表1可见，频率跟踪DFT 方法的分析结果和理论值间的误差很小，幅值相对误差最大为0.69%。

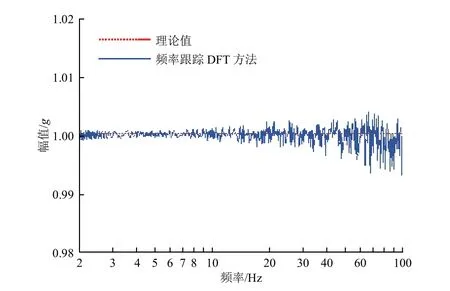
图8 幅值谱理论值和频率跟踪DFT 方法结果Fig.8 The theoretical value of amplitude spectrum and that obtained by frequency tracking DFT

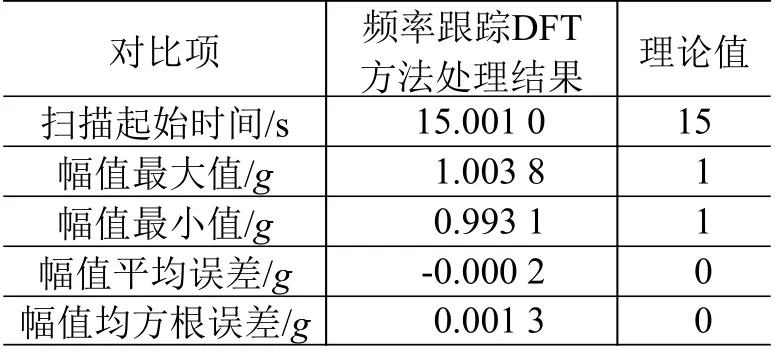
表1 频率跟踪DFT方法处理结果和理论值对比Table 1 Comparison between results obtained by frequency tracking DFT and theoretical value

采样率为400 Hz 时，对扫描速率为4 oct/min 的对数扫频和式(13)描述的二次函数扫频分别使用本文方法进行分析，幅值分析结果与理论值之间的误差见图9（其中，左图为频域幅值谱的理论值和分析结果的曲线，右图为相对误差数据）。可以看到：误差大小和1个信号周期内的采样点个数（即采样频率与信号频率的比值）相关——采样频率大于扫频频率的4倍时分析误差在5%以内，采样频率大于扫频频率的10倍时分析误差在1.5%以内。

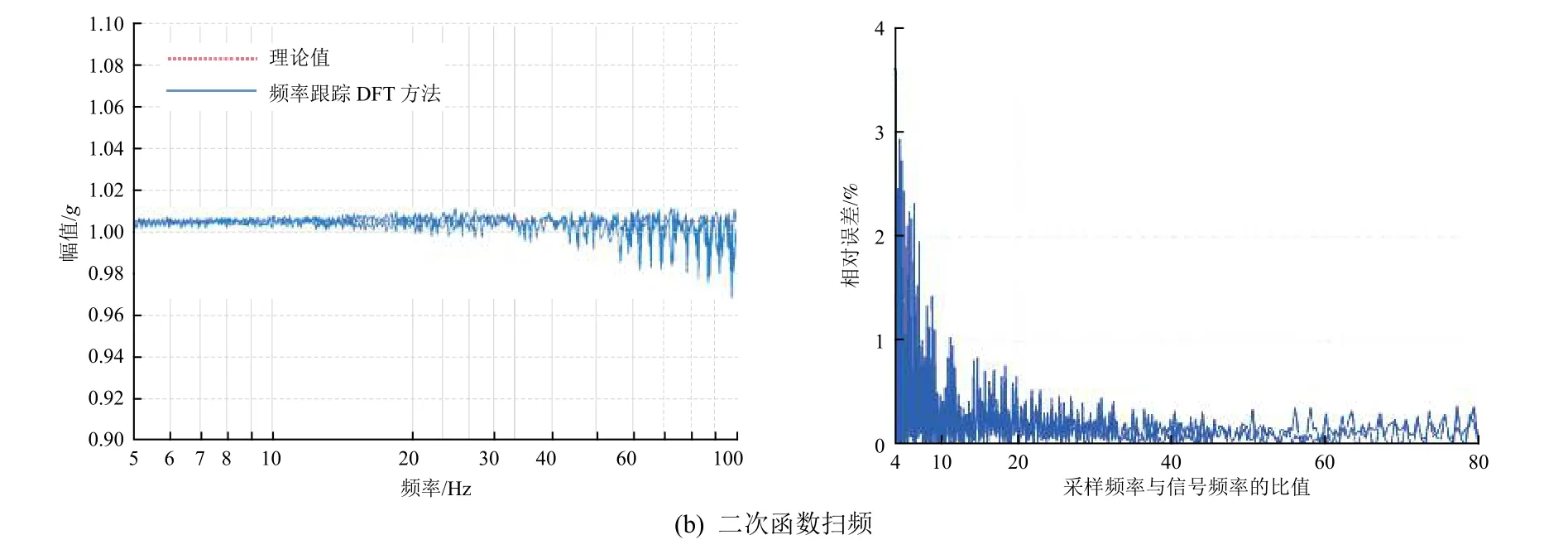
图9 频率跟踪DFT 方法所得幅值谱的误差Fig.9 The errorsof theamplitude spectrum obtained by frequency tracking DFT ascompared with the theoretical values

3.2 与地面数据采集系统幅值谱处理结果对比

使用频率跟踪DFT 方法分析某航天器的正弦振动试验数据，并和地面数据采集系统的滤波方式峰值法处理结果进行对比。

结构振动响应测量点有3个：1号测点在航天器上部，2号测点在航天器中部，3号测点在航天器底部。试验的频率范围为5～100 Hz，扫描速率为4 oct/min。振动激励方向为航天器x方向，同时采集了x向和y向的振动响应时域数据和频域幅值谱数据。时域数据采样率为400 Hz，加速度响应曲线如图10所示（其中，1x、1y分别代表1号测点的x向、y向振动响应，其他依此类推）。频率分辨率为每倍频程100 谱线。

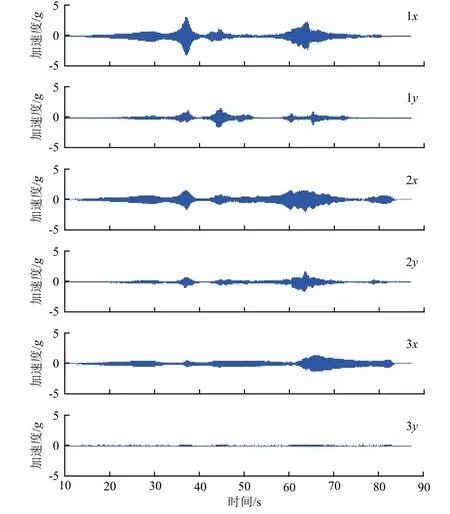
图10 某航天器振动响应时域数据Fig.10 The time domain vibration response of the spacecraft

由于x向是振动激励方向，所以对x向响应数据进行频率识别的精度较高。对3x测点响应数据的频率辨识结果如图11所示，可得到扫描起始时间为16.865 s。振动响应数据采集时使用的是同一套数据采集系统，因此各通道的时域数据对应的时间是同步的，由3x测点得到的扫描起始时间适用于所有通道。

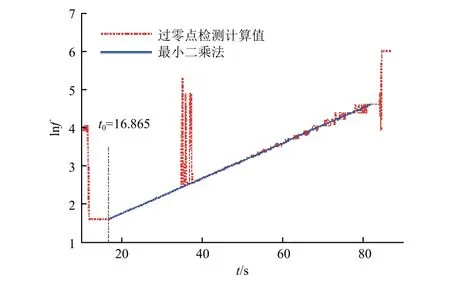
图11 频率辨识结果Fig.11 The frequency identification results

由图11可见，过零点检测法得到的频率值在35～40 s之间存在明显的异常数据，这和结构的一阶频率特性有关。另外，结构响应中的撞击信号也会使该频率检测方法计算得到异常值。使用低频段（5～7 Hz）范围的数据进行最小二乘法频率辨识，可有效避免响应信号中的异常干扰，显著提高频率识别精度。

根据振动试验的扫描起始时间进行频率识别，使用频率跟踪DFT 方法对振动响应数据进行频谱分析，所得频谱曲线见图12，可见分析所得幅值谱和地面数据采集系统的处理结果基本一致，具体误差数据见表2。表2列出了幅值谱曲线的最大峰值及其对应的频率值，对比显示，频率跟踪DFT方法和地面数据采集系统所得结果之间的峰值误差最大为2y测点的1.149 2%，振动激励方向的峰值误差最大为1x测点的-0.369 3%；峰值频率误差最大为-0.688 5%；幅值谱平均误差最大为-0.000 7g，均方根误差最大为0.035 3g，相关系数均在0.99以上。频率跟踪DFT 方法显著减小了非整周期截断引入的频谱分析误差，幅值分析精度和地面数据采集系统滤波方式峰值法的处理精度相差不大。同时，该方法不需要使用窗函数并且可以获得准确的幅值谱，与传统的时频分析方法相比具有明显优势。

图12 频率跟踪DFT 方法和地面数据采集系统所得幅值谱Fig.12 The amplitude spectrum obtained by frequency tracking DFT and the ground data acquisition system

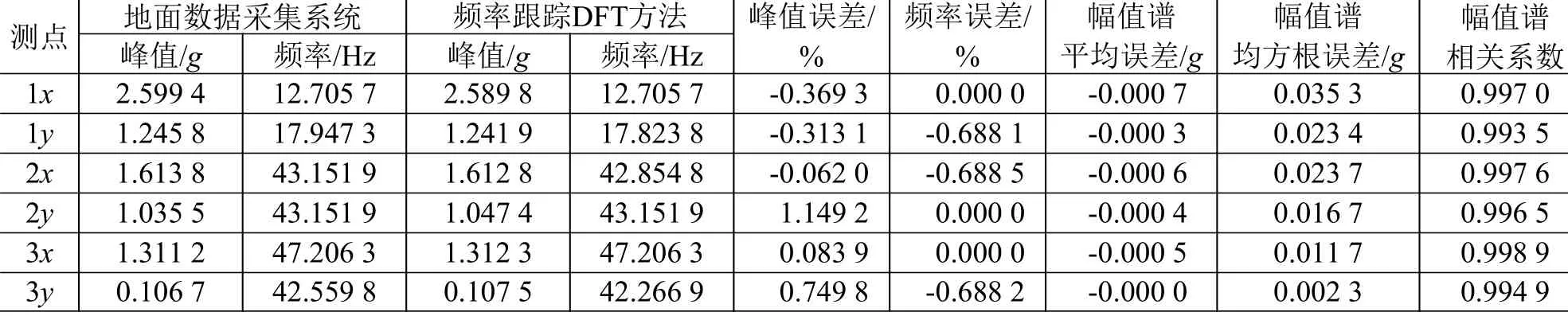
表2 频率跟踪DFT 方法和地面数据采集系统所得结果对比Table 2 Comparison of resultsobtained by frequency tracking DFTand the ground data acquisition system

当时域数据的采样率较高时，非同步采样误差的影响变小，频率跟踪DFT 方法计算得到的幅值谱精度将会更高。当一套数据采集系统同时采集的结构响应数据中没有激振方向的数据时，需要选取和振动控制相关性较好的响应数据进行频率辨识，并进行必要的滤波处理。

4 结束语

本文提出了频率跟踪DFT方法，应用于正弦扫频振动试验数据处理可以得到高精度的幅值谱。该方法不依赖振动控制仪输出的COLA 信号，也不需要数据采集系统对响应信号进行在线频谱分析，对系统的硬件性能要求比较低，有利于发展多通道分布式大型数据采集系统；在时域数据采样率较低的情况下，能得到准确的频谱数据，分析结果和地面数据采集系统的处理结果间误差很小，适用于振动环境试验中航天器在轨力学环境测量系统的有效性验证；使用整周期截断技术避免了传统时频分析方法中的窗函数引入的分析误差。如果对高频段的振动响应分析精度要求较高，可采用针对非同步采样的频谱校正算法进一步提高频谱分析精度。值得一提的是，在结构响应信号失真严重的情况下，该方法的频谱分析精度及适用性有待进一步研究与验证。