中等收入阶段收入差距有效测度建模研究

贾康 苏京春 余乐

【摘要】国内外对收入差距的测度主要在总量和结构两个视角下开展， 不同测度指标具有不同的内涵、特征及实用性。 鉴于此， 将中等收入阶段收入差距的特征概括为以贫富两极差距的结构性矛盾为主并兼顾总量性问题， 指出帕尔玛比值为现有的较为合适的测度指标， 进而构建收入差距测度建模可选取的矩阵分析框架， 并结合框架内的四种组合， 提出我国研究中等收入阶段收入差距的建模思路， 即遵循以帕尔玛比值为核心权重的“三要素”收入差距综合测度表构建的组合IV。

【关键词】中等收入阶段;收入差距;数理分析;测度建模;总量性;结构性

【中图分类号】 F230     【文献标识码】A      【文章编号】1004-0994（2020）23-0116-8

一、中等收入阶段收入差距研究现状

从经济体经济发展至中等收入阶段再到高收入阶段期间， 收入差距究竟是扩大还是缩小， 在很大程度上具有不确定性， 亦揭示出科学、及时、如实地反映收入差距对我国当下发展的重要性。 实际上， 在收入分配过程中， 总量性与结构性问题往往是并存的， 收入差距作为收入分配的最终结果亦受到来自这两个方面因素的影响， 且这两方面之下不同影响路径的反映具有不同的测度方法。

（一）收入差距的总量性研究视角

经济学领域中关于收入差距测度的研究离不开着力形成某一经济体收入差距总体程度的指标构建。 这些指标能够在不同视角下观察、识别某一类群体收入的占比。 沿着学界的研究路径， 可观察到收入差距总量性研究视角下， 从衡量社会总体收入分配不平等程度， 发展至城乡间、区域间以及行业间收入差距这样一条逻辑发展路径。

1. 基于某一类群体收入占比的总量测度。 19世纪末， 随着概率统计理论逐步进入经济学方法论范畴， 意大利经济学家维弗雷多·帕累托通过观察英国收入分配的数据， 首次以概率统计中的最小二乘法（OLS）拟合出高收入群体占总人口的分布函数， 系统性地以数据的形式证实了财富逐步流向高收入群体的事实。 美国社会学家丹尼尔·贝尔以举例的形式， 讲述了帕累托在收入分配上的“二八原则”， 即社会总财富的80%由前20%的人群占有。 也有学者对帕累托收入分配定律做出改进， 并通过欧洲各国的例子， 以帕累托α值判断社会稳定性。 当帕累托α值的绝对值高于1.5时， 高收入阶层将会发动上层革命;当其小于1.5时， 低收入阶层将会发动无产阶级革命。 后续研究中出现了不同形式的统计函数用以测度收入差距， 如伽玛函数、广义伽玛函数、对数正态分布等[1] 。

在测度社会总体收入不平等方面， 广为使用的指标当属基尼系数。 该指标的最初推导也源于统计分布函数， 由意大利统计学家科拉多·基尼提出， 其基于洛伦兹曲线的面积比， 提出总收入和微观个体收入的联合累积分布函数， 用以测度社会总体收入不平等， 即整体的收入差距程度可视为洛伦兹曲线与完全平等曲线之间的面积（B）与总面积（A）之比（B/A）[2] 。 后续研究者主要基于基尼系数的新方法并结合各国实践应用， 开展内容更为丰富的研究。 随着数理方法的发展， 从曲线面积法、基尼均值法到协方差法、矩阵推演法等， 经济学家们将不同数学方法应用于基尼系数的计算， 如杨小凯[3] 避免了各类概率密度函数分布式较为繁琐的缺陷， 将回归方程与洛伦兹曲线相结合， 以较为简便的方式推导出基尼系数。 李实等[4] 通过对我国不同家庭收入、消费数据的抽样方法的商榷， 指出不同的数据结构偏差将对基尼系数产生显著高估、低估。 有学者利用基尼系数检验了其与经济增长率之间的定量关系， 发现低收入国家经济落后的主要原因在于巨大的收入差距[5] 。 但也有学者对此提出异议， 认为基尼系数具有仅限于静态测度的局限性， 难以反映一段时期内收入差距的情况， 并且難以甄别出不同原因引起的收入差距。

2. 总量测度的多样性发展。 随着基尼系数局限性的逐步显现， 学者们开始聚焦于对基尼系数的分解， 以博弈论的方法将其进一步划分为组间差距、组内差异等[6] ， 或以群体类别为依据将其划分为城乡间、地域间以及行业间组别， 再利用基尼系数计算不同组别间的收入差距。 李实等[7] 以居民身份为依据， 将基尼系数划分为总基尼系数、农村居民基尼系数与城镇居民基尼系数， 对比得出农村居民收入差距远高于城镇居民。 还有学者以基尼系数为基础， 测度我国东部地区与中西部地区之间收入初次分配、再分配的公平程度[8] ， 以及石油、电力等部分国有企业因其行业性垄断存在的行业间收入差距、国有企业与非国有企业之间的收入差距等[9-11] 。

（二）收入差距的结构性研究视角

从全球经济体发展实践来看， 当某一经济体从低收入阶段发展至中等收入阶段的过程中， 收入差距现状呈现出结构性问题：社会总体收入偏低， 贫困群体占比偏高[12] 。 拉丁美洲经济历经“失去的十余年”， 各国政府无财政约束的福利政策拖垮经济、提高失业率， 导致中低收入者剧增， 使得收入差距进一步扩大[13] 。 在拉美“福利陷阱”现象的基础上， 可观察出拉丁美洲各国在收入分配政策方面错误的战略导向[14] 。 经济学者基于拉丁美洲经济发展不平衡现象提出“中心—外围”经济结构主义理论。 这一方法论开拓性地颠覆了一般均衡理论对经济事物“同质化”的假设， 转而探究其内部分布的多维度、多层次等异质性特征。 借鉴结构分析方法， 本文将某一类收入差距测度结果归纳为结构性问题， 首先通过复杂的社会福利函数辨别出收入差距的公平程度， 然后运用简单的比值运算甄别要素间收入回报的差异性。

1. 公平分配的结构性问题。 收入差距的公平研究往往涵盖规则公平、过程公平及结果公平等[15] ， 归结到理论层面则可从社会福利视角考察分配的结果， 如安东尼·阿特金森认为微观个体的均值收入越接近于社会总体收入的均值， 意味着公平程度越高， 其结果为阿特金森指数（A?）越小[16] 。 阿特金森指数被提出之后， 诸多研究围绕社会福利函数构建的前提去探寻测度指标的最佳值， 具有更强的经济含义， 由此出现了不同福利函数下多种较为复杂的阿特金森指数， 如功利主义阿特金森指数、纳什阿特金森指数和罗尔斯主义阿特金森指数等， 用以测度同一地区的收入差距情况， 其结果呈一致性[17] 。

2. 动态考察要素间收入回报的结构性差异。 托马斯·皮凯蒂[18] 在《21世纪资本论》中创设了一个测度收入差距的新指标——资本与收入的比值， 其使用最为简单的“除法”数学运算来构建新指标， 却能甄别出收入差距形成的结构特征， 反映“资本收益远超经济增长”的要素间回报的差异性事实。 该比值意味着可鼓励劳动创造所带来的收入差距， 而需逐步抑制纯资本增值所形成的差距， 如财富继承。

皮凯蒂等在对中国社会收入差距的研究中， 描述了改革开放近40年中国社会的情况， 即资本与收入的比率从350%增加至700%， 公共财产却在国民财富中的份额下降， 由70%降至30%， 以此有针对性地提出实施高额累进所得税、遗产税等调节高收入群体的税制改革[19] 。 简单的数理计算方法可应用于动态考察收入差距的演变， 皮凯蒂等利用该指标和详实的个人所得税报税数据， 证实了库兹涅茨所设定的1913 ～ 1948年为期35年的观测期收入差距的图形确实是倒U型， 但1950 ～ 1970年美国社会的收入差距趋于稳定， 而1980年之后收入差距并没有随着美国“新经济”时代的到来而出现弥合， 反而重新扩大至1913年的差距水平[20] 。 然而， 颇具影响力的达隆·阿西莫格鲁等指出， 资本与劳动的收入比值难以甄别出其他要素与劳动、资本的结合， 如技术创新、制度变迁等因素与劳动、资本所结合形成的收入差距， 因此简单地以此作为高额税制的施政依据， 或将产生驱赶高新科技人才、抑制科技资本增值等负面作用[21] 。

（三）中等收入阶段收入差距的特征

通过对反映收入差距总量性与结构性问题的表征方式进行分类梳理， 可归纳出中等收入阶段收入差距的特征， 即以贫富两极差距较大等结构性问题为主、双重问题并存的现实。 而对这一特征的准确识别则成为中等收入阶段收入差距测度建模的关键目标之一。

收入差距的表征方式存在问题表现上的相互割裂、单一而难以兼顾等弊端， 但个别现有指标依然能够较为合适地反映出此阶段的特征。 英国经济学家帕尔玛提出了一个能够较为妥善地兼顾总量性与结构性问题且突出表达贫富两极差距特征的测度指标， 即全社会前10%人群与后40%人群收入份额的比值[22] 。 亚历克斯·科巴姆和安迪·萨姆纳提出了以帕尔玛比值作为描述收入差距的有效方法论[23] 。 英国经济学家帕尔玛等将帕尔玛比值与基尼系数进行对比分析， 说明了帕尔玛比值测度对以拉美国家为首的发展中经济体收入差距的适用性[24] 。 也有学者通过计量方法证实了帕尔玛比值的可靠性[25] 。 还有学者指出， 开放市场下国际资本流动通过干预生产条件、套利等方式， 加大了中国前10%高收入与后40%低收入群体的收入差距[26] 。

近年來， 帕尔玛比值的提出及应用弥补了中等收入阶段收入差距现实问题表征的缺失， 究其原因：第一， 能准确甄别出特征。 经济不同发展阶段对应了不同原因造成的收入差距问题， 而中等收入阶段正是一个经济体爬坡上坎的关键时期， 在此时期， 后发优势使得一部分人率先富裕， 造成全社会贫富差距两极分化， 国民收入差距显著增加。 由此， 更能反映两极差距的帕尔玛比值恰能准确识别其特征。 第二， 数据日趋丰富。 全社会收入分配的研究离不开详实的微观个体收入数据， 现阶段入户调查采集工作的完善、基于平台的消费大数据估计等科技的应用， 有效助力了收入差距问题的研究工作。 第三， 方法更“接地气”。 收入差距问题表征的推导过程贴近现实远比推导本身所用的复杂数理计算更为重要， 并且更贴近现实的表征推导方式也更容易与微观数据相结合， 加快其应用研究进程。

二、中等收入阶段收入差距测度指标及特征

在有关研究中经济学家们创造了诸多测度收入差距现状的方法， 本文基于第一部分的研究， 在当下学界所涉及的系数、指标、曲线以及比值中， 选取具有代表性的指标进一步考察， 不难发现， 它们分别基于不同的构建方法为我们提供了测度中等收入阶段收入差距总量层面和结构层面的指标， 其中也不乏兼具总量与结构两个层面的指标。

（一）收入差距的总量性测度指标：帕累托α值和基尼系数

1. 帕累托α值：收入差距总量的粗糙测度。 1897年， 帕累托利用已有的不完整的统计数据， 归纳出“收入分配定律”， 并构造了高收入群体的收入分布式：N=AY-α（对数形式为logN=A-αlogY）。 其中：A和α是统计量， 由最小二乘法拟合该方程得到;Y为收入分布（高于社会总收入的中位数）;N为收入高于中值的人数比率。 帕累托使用经验统计学的数据整理方法， 利用长期数据估计出α值集中分布的区间为[1.5，1.7]， 并获得规律性结论：收入差距越小， α值越大; 反之亦然。

随着经验统计数据日趋完整与丰富， 帕累托α值在实践中出现了矛盾现象。 究其原因：一方面， 帕累托在构造α统计量时数据不够完整， 尤其是缺少中低收入人群样本的数据;另一方面， 在经验统计方法上使用最为简单的最小二乘法进行拟合， 但该方法的应用基于参数线性等严格的假设条件， 背离了经济实际。 因此， α值这一测度指标实质上已失去了价值。

2. 基尼系数：收入差距总量的精细测度。 长久以来， 意大利统计学家科拉多·基尼提出的基尼系数被人们广泛用来测度某一经济体的收入差距。 现阶段， 世界银行、国际货币基金组织以及各国政府的统计部门也广泛使用基尼系数来评价收入差距。 该系数基于“洛伦兹曲线”， 以图示面积法推导而来， 其样本选取全社会口径的微观家庭收入。 系数值分布在0与1之间， 越接近于1， 意味着全社会整体收入差距越大， 越靠近于0， 则意味着分配越公平， 目前通行的警戒线标准为0.4。

基尼系数推导的数理方法具有均值统计量的特性， 其优点在于大样本下可全面反映样本的离散程度， 即个人或者家庭中收入差距偏离统计均值的程度。 但由于这一数理特性， 基尼系数也存在一定的缺陷：第一， 大样本下仅能反映出收入差距的总量特征， 难以深入至收入差距的结构性问题。 第二， 难以直观认识基尼系数持续走高的经济原因， 进而探寻缩小收入差距的政策建议。

（二）收入差距的结构性测度指标：阿特金森指数和资本与收入的比值

1. 阿特金森指数：收入差距的相对结构测度。 英国经济学家安东尼·阿特金森认为， 现有收入差距测度指标如基尼系数、统计理论中的方差和离差等， 虽从表象上避开了社会福利分析， 但社会福利函数是隐含在上述测度指标的推导之中的。 以此分析， 他构建了融入价值判断的更为综合的测度指标， 即阿特金森指数（A?）。 该指数将社会福利函数显性化， 明示其测度指标的公平观， 该指标以概率密度函数形式表征：A?=1-y?/μ。 其中：μ表示平均收入;y?为等价敏感平均收入， 是实际收入yi的概率密度函数， 可理解为公平分配时的收入水平， ε为不平等厌恶参数。 y?与μ越接近， 表示收入差距越小， 意味着当平均收入相等时， 收入分布函数表征的结果差距将导致社会福利更低。

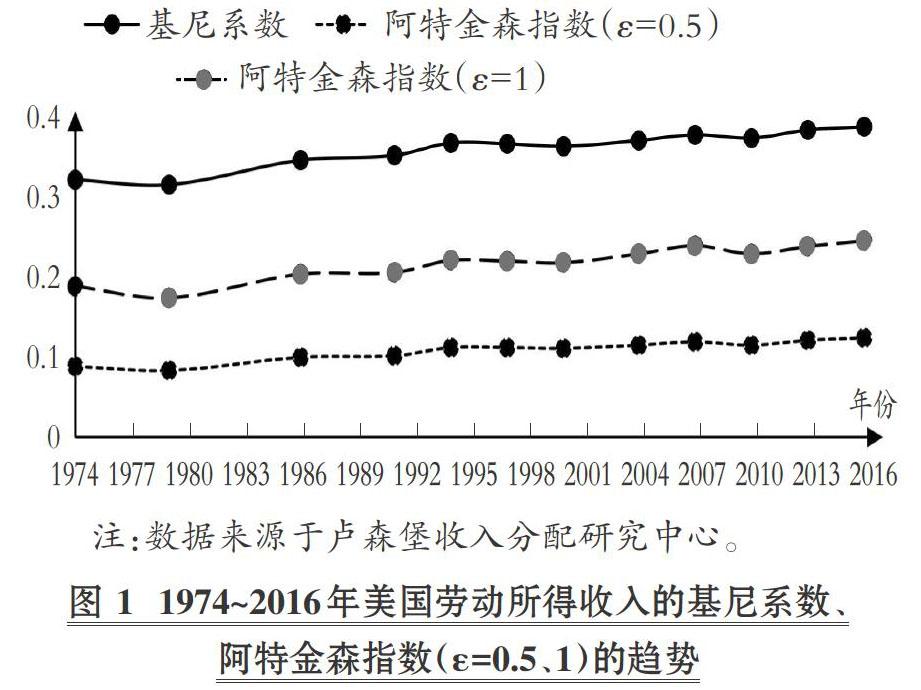
相较于基尼系数等直接测度人与人之间收入分配的差距， 基于不同类别社會福利函数构建的阿特金森指数的优势在于， 其更关注社会总福利分配下的收入差距。 图1刻画了1974 ～ 2016年美国劳动所得收入的基尼系数、阿特金森指数（ε=0.5，1）的趋势。

由图1可知：第一， 从收入差距测度指标总量的趋势来看， 美国社会的劳动所得收入差距逐步扩大。 第二， 阿特金森指数中ε表征的是不平等厌恶程度， 可理解为基于社会福利函数考虑的人们对收入差距的偏好情况。 就经济现实来看， 基尼系数的不平等厌恶程度向中等收入群体赋予了更多的权重， 而基于社会福利函数的阿特金森指数中的ε为[0，∞）， 即随着赋值的增加， 函数的权数更多赋予低收入群体， 这样的权重转移赋值计算方法在实际生活中能观测出微观个体间相对收入的结构性变化比例。 第三， 阿特金森指数与其他统计指标、基尼系数相比， 是收入差距测度指标从总量性测度转向结构性测度的开端之一， 其原因往往在于基于社会福利函数所构建的指标赋值方式， 体现了微观个体间的相对收入变化比例， 但不足之处在于， 当各社会阶层发生同比例的结构性变化时， 该指标测度会失效， 即微观个体间绝对的收入差距难以测度， 这意味着难以反映出如托马斯·皮凯蒂[18] 所言的“穷人更穷、富人更富”的资本主义社会收入差距演化状态。

2. 资本与收入的比值：收入差距的绝对结构测度。 托马斯·皮凯蒂[18] 构造了一个全新的测度收入差距的指标——资本与收入的比值（r/g）。 他认为， 基尼系数等收入差距总量性测度指标“一刀切”地评估一国经济体发展过程中收入差距的大小， 不尽科学， 原因在于收入可进一步结构性地划分为劳动所得、资本所得， 鼓励劳动所得形成的收入差距， 可促进经济增长。

从2005 ～ 2015年美国社会各阶层群体税前劳动收入占国民总收入的分布来看， 劳动所得收入占比最多的仍为中产阶级及中产以上阶级， 这也是美国基尼系数偏高、收入差距总量性测度指标较大， 但美国经济增长率仍较高的关键原因之一。 有鉴于此， 皮凯蒂综合了流量概念的劳动所得与存量概念的财富继承等所得， 构造了资本与收入的比值指标， 以表征长期以来资本所得是否向高收入阶层集聚。 以此理论联系实际， 资本与收入的比值越高， 说明占有相对较多的储蓄、投资以及回报机会的极少数高收入群体， 越多地拥有了该国资本所得收入， 由此在收入分配政策调控方面， 应对其施行累进所得税以及增加低收入群体的社会福利支出等。

皮凯蒂构建的资本与收入的比值指标将收入结构性地划分为财富与劳动所得， 其在表征收入差距时， 既弥补了基尼系数等难以测度收入结构特征的缺陷， 又改进了阿特金森指数仅能测度相对收入差距的不足， 可用以测度绝对收入差距， 阐释“富人是否更富， 穷人是否更穷”的关键性命题。 但劳伦斯·萨默斯、格里高利·曼昆以及德隆·阿西莫格鲁等从资本贬值、技术革命、全球化扩张、个税政策以及制度等多角度， 质疑了其测度方法的科学完备性。

（三）兼具总量性与结构性的收入差距测度指标：帕尔玛比值

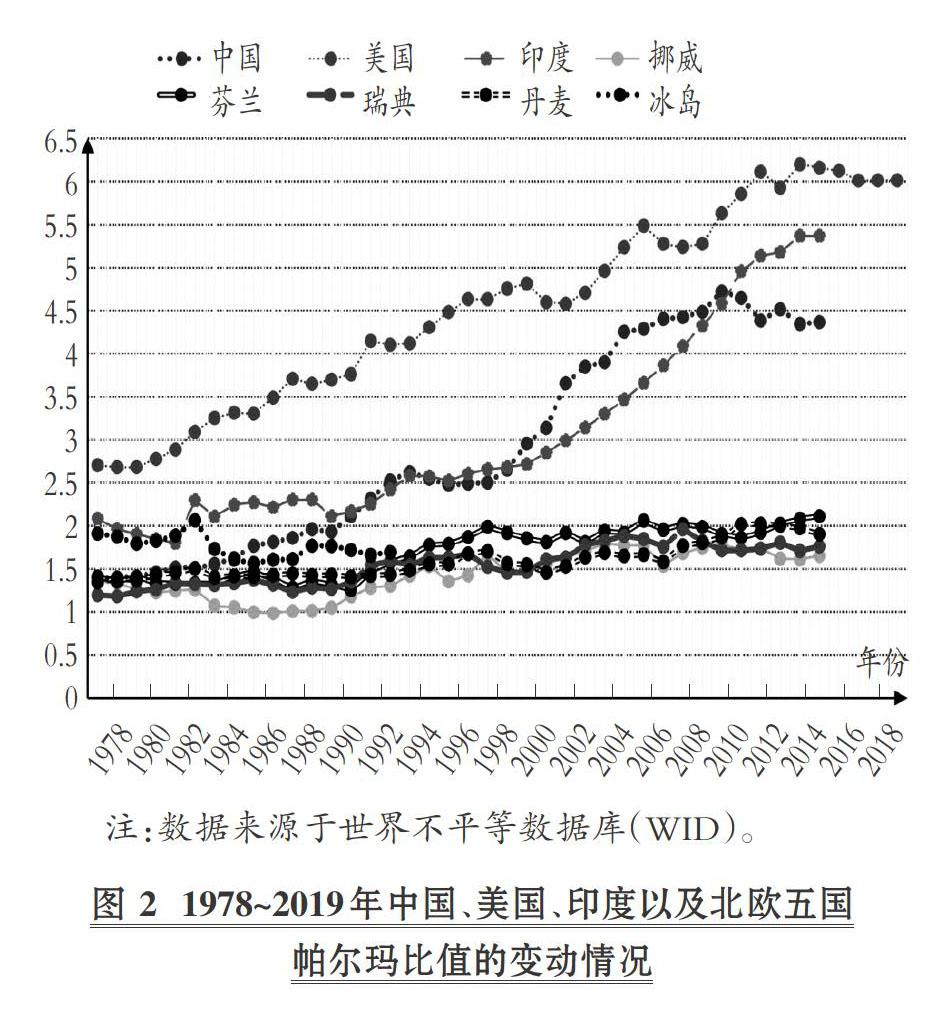
英国经济学家帕尔玛通过对135个国家1990 ～ 2010年的收入数据进行整理， 发现收入状况处于社会整体收入50%的群体在此期间所占的份额保持相对稳定， 对全社会收入差距结构变化的影响不大， 由此提出了一个新的测度指标， 即在测度时忽略处于中等收入的50%群体， 重点关注位于贫富两极的前10%与后40%群体收入份额的比值， 这样可敏感地测度出贫富两极的差异[22] 。 如图2列式了1978 ～ 2019年中国、美国、印度以及北欧五国帕尔玛比值的变动情况。

由图2可知：第一， 从总量特征来看， 长期以来北欧五国的帕尔玛比值平稳地处于较低状态， 符合通常认知中的“中间多、两极少”的“橄榄型”收入分配格局; 而美国、印度的帕尔玛比值长期以来持续走高， 印度的帕尔玛比值更是逐年直线上升， 符合“哑铃型”收入分配格局。 第二， 与基尼系数对比看其结构特征， 图3展示了1996 ～ 2016年中国基尼系数的变动情况。 由图3可知， 中国基尼系数也呈现出先逐年上升后略有下降的趋势， 但难以从指标中直接观察出下降的原因。 相比之下， 从图2来看， 中国改革开放以来， 东部地区率先发展， 国民收入差距逐渐扩大， 帕尔玛比值逐年上升。 而近年来， 在中国政府以“坚决打赢脱贫攻坚战”为目标的减贫政策的调控下， 贫困人口显著减少， 国民收入差距的结构性矛盾得到有效改善， 帕尔玛比值明显降低， 并且从帕尔玛比值的定义可直接观察其下降的原因在于减贫政策调控后贫困人口数显著减少。

综上所述， 如果对测度指标的方法论发展进行观察， 不难发现测度指标随着数理研究方法论的日趋成熟， 亦呈现出从单一方法向综合方法的发展逻辑; 如果对测度指标本身进行观察， 可以发现沿着时间序列， 其表现出较为明显的由总量向结构的发展逻辑， 即测度收入差距总量从粗糙表征的帕累托α值到精细表征的基尼系数， 再演变为测度收入差距结构的绝对差距以及相对差距。

三、中等收入階段收入差距测度矩阵分析框架的构建

基于理论联系实际的方法， 为便于比较、分析与观察收入差距测度建模的实现路径及其预期发展， 我们试借鉴数学中的矩阵特征， 总结其规律， 构建收入测度矩阵分析框架。

（一）为收入差距测度引入矩阵分析框架

本文借鉴矩阵的图形形式， 构建出收入差距测度建模矩阵分析框架， 即从收入差距方法论视角将收入差距测度方法划分为两大类：一是测度指标推导及使用的方法论视角， 分为单一的和综合的;二是测度指标应用于测度收入差距问题类型视角， 分为总量性的和结构性的。 四种情况的排列组合可形成不同收入差距方法论的四类情况， 如图4所示。

此分析框架基于收入差距及其测度的方法论与测度指标应用视角提炼出理论与实践的要领， 并将现有的收入差距测度指标按其对应特征归类划分为四种组合。

1. 组合I：测度收入差距总量， 方法论单一。 其特征为测度指标主要应用于观察与度量收入差距的总体情况， 并且所使用的是具有严格限制、理想化的单一数理方法， 其测度结果偏于粗糙， 与真实收入差距结果可能相距甚远， 且不可验证其偏离程度。 对此可作如下分析：随着概率统计知识进入经济学研究范畴， 利用统计分布函数构建出以有限数据收集仅针对高收入群体的收入分布函数的帕累托α值， 在其推导方法方面， 由于分布函数求解方法的限制， 仅使用了具有严格推导假设的最小二乘法。 因此， 以此连续函数描述的收入差距测度指标理想化程度较高。

2. 组合II：测度收入差距结构， 方法论单一。 其特征为测度指标主要应用于观察与度量收入差距的结构情况， 并且所使用的是单一数理方法， 其测度结果主要反映收入差距的结构， 但该方法忽略了影响收入分配的其他变量， 使得其在实际应用中的参考价值降低。 对此可作如下分析：随着经济发展中收入差距现象的日益普遍， 收入差距的总量性测度指标虽可表征其现象的均值增长水平， 但就政策实践层面来看， 无法根据收入差距的均值水平对症下药、精准施策。 其根本原因在于， 总量性测度指标难以辨别收入差距现象是中产阶级缺失还是高收入与低收入群体差距过大所致。 与此同时， 经济增长与收入差距又存在交集影响因素， 区分劳动、资本等不同要素对收入差距的影响就显得尤为重要， 但上述种种现实情况均难以通过总量性测度指标反映出来。 因此， 随着实际收入分配数据的日趋详实， 测度收入差距的结构性指标应运而生。

3. 组合III：测度收入差距总量， 方法论综合。 其特征为测度指标主要应用于观察与度量收入差距的总体情况， 但使用了较为丰富、综合的数理方法论， 从不同角度、逐渐演进地精确测度收入差距的中位数值， 但仍无法反映收入差距的结构性问题。 对此可作如下分析：相比单一数理方法推导出的粗糙总量测度， 随着收入差距数理方法论的逐渐丰富与收入差距数据的日益详细， 测度收入差距中位数值的准确性显著提高。

4. 组合IV：测度收入差距结构， 方法论综合。 其特征为测度指标主要应用于观察与度量收入差距的结构情况， 并且使用了较为丰富、综合的数理方法论， 从不同角度、相互印证地精确测度收入差距的结构分布， 用以准确反映收入差距的结构性问题。 对此可作如下分析： 对于中国、印度等处于中等收入阶段的发展中经济体而言， 这样的测度方法可以甄别出贫富两极收入群体的份额占比、贫富两极资产与劳动对收入的贡献程度、公平分配的程度以及社会总体收入状况， 由此可更准确地综合描述此发展阶段的收入差距状况。 就现有指标来看， 帕尔玛比值因其对贫富两极的敏感甄别而颇为合适， 但其数理方法论综合性仍有待改进， 如尚不能甄别出不同群体可占有不同要素的难易程度以及要素间形成收入差距的差异。 根据上述指标的综述， 笔者提出通过构建以帕尔玛比值为核心权重的“三要素”收入差距综合测度表， 待测数还包括资本与收入的比值和阿特金森指数， 共三种指标， 以此多维度综合评价中等收入阶段的收入差距。

（二）四种组合与中等收入阶段收入差距测度实现路径

本文提出的分析框架的四大区域， 对应收入测度建模实现路径的四种组合。 其中， 组合IV即以帕尔玛比值为核心权重的“三要素”收入差距综合测度表， 应是中等收入阶段收入差距测度较为适合的建模路径。 原因有二：第一， 以旨在甄别贫富差距的帕尔玛比值可甄别出此阶段收入两极分化的主要问题， 而造成两极分化的重要原因， 如要素间回报差异、分配过程的公平性等， 则可利用资本与收入的比值和阿特金森指数辅助识别。 第二， 帕尔玛比值兼顾了总量性与结构性问题两种特征。 一方面， 中等收入阶段收入差距仍具有低收入阶段的特征， 呈现出社会总体收入偏低的情况， 因此仍需刻画收入差距总量情况， 而帕尔玛比值也可描述出如“哑铃型”“橄榄型”等不同国民收入分配格局;另一方面， 基于对中等收入阶段收入差距的特征判断， 其以贫富差距为主的描述恰好与帕尔玛比值的定义相适应， 因此甄别的敏感性较强。 由此可见， 在此时期收入差距建模应采用系统性测度表形式， 以甄别贫富差距的结构性矛盾为主、总量性问题为辅。 其中， 收入差距测度建模中帕尔玛比值权重较高， 是该表构建的关键， 具体建模思路如图5所示。

四、研究结论与启示

从收入差距视角来看， 在低收入阶段发展至中等收入阶段期间， 由于全社会低收入群体规模偏大、中高收入群体缺乏， 收入差距总量性问题突出; 随着经济的高速增长， 在中等收入经济体向高收入阶段迈进时期， 有限经济红利不为全社会所共享， 导致贫富差距增大、资本收益率增长过快以及分配公平程度降低等， 收入差距呈现出结构性矛盾。 在冲关过程中， 如不能妥善解决突出的结构性矛盾， 或将陷入“中等收入陷阱”的恶性循环局面。 对此， 本文构建了中等收入阶段收入差距测度建模的矩阵分析框架， 以组合IV中的建模思路， 试总结出以下启示。

（一）聚焦中等收入阶段， 合理选取矩阵组合

现阶段我国收入差距所面临的问题更偏重于结构性矛盾， 但并不意味着不存在总量性问题， 因此， 在选取测度建模的组合时， 需要兼顾灵活适度原则， 组合IV中提出的以帕尔玛比值为核心权重的“三要素”收入差距综合测度表， 既要以结构性指标为主识别冲关阶段存在的因经济结构调整不到位所衍生的分配问题， 又要适时跟踪全社会的收入差距现状， 以防返贫风险。

另外， 灵活适度体现在不能就指标论指标， 如皮凯蒂的资本与收入的比值指标难以甄别出由技术创新带出“新经济”中资本积累引致的收入差距扩大现象。 随着互联网的兴起， 我国依托巨大的人口规模、市场潜力和改革赋能优势， 对接全球互联网产业链需求侧， 在供需互动中历经计算机技术模仿、追赶阶段， 诞生了以阿里巴巴等为代表的中国互联网科技巨头。 由此， 现阶段的中国社会又产生了对“寡头垄断”的热议， 其要义正涉及对由技术创新带出资本积累引致的收入差距扩大问题的反思。 现有的最接近于测度各阶层间收入差距的结构性指标， 即皮凯蒂的资本与收入的比值指标， 虽然该指标区分了劳动所得与资本所得， 进而从政策层面鼓励劳动所引致的收入差距扩大， 以此形成良性的正向激励市场制度， 但其对资本所得是予以抨击的， 需要通过税收等方式来改善收入差距。 追本溯源， 皮凯蒂的初始研究对象为欧洲， 尤其是英法两国的收入分配。 从产业革命的发展历程来看， 以信息技术为代表的“新经济”现象未在欧洲各国形成最有代表性的表现。 因此， 资本与收入的比值指标对技术创新引发财富积累、收入差距扩大现象的分析和认识不足。 从中国的现实层面来看， 对互联网科技巨头企业所存在的“寡头垄断”需要再认识， 垄断经济会抑制竞争和创新且减少社会总福利， 但数字技术与企业结合后并没有减损社会福利， 反而是基于一定的规模门槛提升了社会福利的必要“头部”状态。 鉴于此， 技术创新引发财富积累、收入差距扩大这类现象与劳动所带来的差距扩大一样， 有值得肯定的一面。

（二）注重数据的详实整理， 跟踪观测收入差距

梳理收入差距測度指标的发展规律可知， 一方面， 随着数理理论进入经济学的方法论视野， 收入差距的研究也从古典经济学中定性分析的分配理论转向定量研究。 如概率统计理论促进帕累托首次提出以统计分布函数形式描述的收入分配定律， 但由于当时数据的缺失， 该指标仅能有限判别高收入群体的分布。 另一方面， 随着计算机技术的发展和大数据时代的到来， “数据为王”“数据霸权”等现象也出现在经济学研究领域中， 尤其在收入差距的研究中， 库兹涅兹理论得到广泛热议， 此后的研究者多以不同计量方法证实了倒U型曲线的存在性， 但由于计量方法本身具有一定的数学限制， 其适用性仍存在一定争议。 然而， 托马斯·皮凯蒂[18] 以更为长期的丰富数据颠覆了倒U型曲线推导中所使用的相对短期的数据结论， 其对全球各个经济体详实的数据整理， 尤其是构建的WID数据库， 如今更成为全球收入差距研究的焦点。

观察我国同一时间收入差距测度的不同结果， 即世界银行的基尼系数0.385（数据来源于世界银行2016年基尼系数）， 以及皮凯蒂以资本与收入的比值指标测出的“2016年中国社会财富占比前10%的居民占总财富的67%”[19] ， 从前者来看， 收入差距不算大， 但从后者来看， 贫富差距现象严重。 将不同维度的指标进行对比固然有其不合理性， 但最终指向都是需整理出更为丰富的收入差距数据， 以更加合理地估算我国收入差距的真实情况。 如借鉴皮凯蒂使用的原始资料（如个人所得税申报单）， 而现阶段我国个税申报的电子化、数字化恰好形成了研究收入差距现状的第一手素材。

（三）数据与调研相结合， 综合评估实际情况

组合IV中提出的建模思路， 即构建“三要素”收入差距综合测度表， 其实质是多维度、层次化以及结构化地识别中等收入阶段收入分配过程中的特征， 而从经济理论层面来看这些特征或都是一定制度因素所致。 正如德隆·阿西莫格鲁等[27] 在《国家为什么会失败》一书中提出的制度二分的方法， 即攫取性与包容性， 相对劣势在收入分配制度上的攫取性体现为收入关联的计划性配置资源特征明显。 宏观视角下， 缺乏全社会各行业、各阶层人力资本的竞争性报酬机制; 微观视角下， 社会成员的工资固定而刚性， 未与以市场在资源配置中起决定性作用的调节机制相衔接， 生产者收益集中分配， 缺乏生产性劳动激励。 由此产生的收入差距的结构性因素在于配置资源的主体权力倾向， 接近权力核心的社会群体与远离权力核心的社会群体形成收入差距。

由此可见， “三要素”收入差距综合测度表可以全面评估实际收入差距情况的关键原因在于其更多地考察和分析了实践层面的具体情况。 如帕尔玛比值构建的前提条件是根据观察得出中等收入群体的稳定性较高， 但我国的现实表明， 中等收入群体具有不确定性， 因病残致贫、返贫等由于社会兜底政策不到位导致的现实偶发情况， 教育资源的不均衡导致的阶层间代际滑落， 城乡间户籍制度的限制造成人才流动的阻滞等， 都值得纳入研究分析视野。 因此， 结合我国的具体实践来看， 除了数据系统表征， 将实地案例调研反映在建模中也尤为重要。 综上， 收入差距测度模型除了需要进行详实的数据收集整理、使用科学的计量分析方法， 还应结合有一定样本规模的案例调查分析， 这样才有助于提高对收入差距现实情况的认识水平。

【 主 要 参 考 文 献 】

[1] Salem A. B. Z.， Mount T. D.. A Convenient Descriptive Model

of Income Distribution：The Gamma Density[ J].Econometrica，  1974（6）：1115 ～ 1127.

[2] Gini C.. Measurement of Inequality of Incomes[ J].The Economic

Journal，1921（121）：124 ～ 126.

[3] 杨小凯.社会发展的重要经济指标——基尼系数[ J].武汉大学

学报（社会科学版），1982（6）：73 ～ 76.

[4] 李实，万海远.提高我国基尼系数估算的可信度——与《中国家

庭金融调查报告》作者商榷[ J].经济学动态，2013（2）：43 ～ 49.

[5] Barro R. J.. Inequality and Growth in a Panel of Countries[ J].

Journal of Economic Growth，2000（1）：5 ～ 32.

[6] Anon. On the Interpretation and Disaggregation of Gini Coeffi-

cients[ J].The Economic Journal，1976（342）：243 ～ 255.

[7] 李实，朱梦冰.中国经济转型40年中居民收入差距的变动[ J].

管理世界，2018（12）：19 ～ 28.

[8] 孙敬水，赵倩倩.中国收入分配公平测度研究——基于东中西

部地区面板数据的比较分析[ J].财经论丛，2017（2）：18 ～ 27.

[9] 蔡昉，都阳，王美艳.中国劳动力市场转型与发育[M].北京：商

务印书馆，2005：1 ～ 276.

[10] 夏庆杰，李实，宋丽娜等.国有单位工资结构及其就业规模变化

的收入分配效应：1988-2007[ J].经济研究，2012（6）：127 ～ 142.

[11] 王询，彭树宏.中国行业工资差距的演化与特征[ J].中国人口

科学， 2012（5）：47 ～ 55.

[12] 蔡昉.中国经济如何跨越“低中等收入陷阱”？[ J].中国社会科

学院研究生院学报，2008（1）：13 ～ 18.

[13] 樊纲，张晓晶.“福利赶超”与“增长陷阱”：拉美的教训[ J].管理

世界，2008（9）：12 ～ 24.

[14] 贾康，苏京春.直面“中等收入陷阱”真问题——基于1962-

2013年全球数据对“中等收入陷阱”的判断、认识[ J].中共中央党校学报，2015（9）：51 ～ 63.

[15] 贾康.论居民收入分配中政府维护公正、兼顾均平的分类调节

[ J].地方财政研究，2007（7）：4 ～ 7.

[16] Atkinson A. B.. On the Measurement of Inequality[ J].Journal

of Economic Theory，1970（3）：244 ～ 263.

[17] 欧阳葵，王国成世社会福利函数与收入不平等的度量——一个

罗尔斯主义视角[ J].经济研究，2014（2）：87 ～ 100.

[18] 托马斯·皮凯蒂著. 巴曙松等译.21世纪资本论[M].北京：中

信集团出版社，2014：1 ～ 740.

[19] Thomas Piketty， Li Yang， Gabriel Zucman. Capital Accumula-

tion， Private Property and Rising Inequality in China， 1978-2015[ J].American Economic Review，2019（7）：2469 ～ 2496.

[20] Thomas Piketty， Emmanuel Saez， Gabriel Zucman. Distribu-

tional National Accounts：Methods and Estimates for the United States[ J].Quarterly Journal of Economics，2018（2）：553 ～ 609.

[21] Daron Acemoglu， Pascual Restrepo. The Race Between Man

and Machine：Implications of Technology for Growth， Factor Shares， and Employment[ J].American Economic Review，2018（6）：1488 ～ 1542.

[22] Palma J. G.. Homogeneous Middles Vs. Heterogeneous Tails，

and the End of the "Inverted U"： It's All about the Share of the Rich[ J].Development and Change，2011（1）：87 ～ 153.

[23] Alex Cobham， Andy Sumner. Is It All about the Tails？ The Palma

Measure of Income Inequality[Z].Center for Global Development Working Paper，2013.

[24] Palma J. G.， Stiglitz J. E.. Do Nations Just Get the Inequality

They Deserve？The "Palma Ratio" Re-examined[M].London：Palgrave Macmillan，2016：35 ～ 97.

[25] 張涛.中国收入差距的变动及其原因分析：1985～2012年[ J].

数量经济技术经济研究，2016（12）：3 ～ 22.

[26] 黄泽清，陈享光.国际资本流动与我国各收入群体收入份额的

变动——基于帕尔玛比值的分析[ J].经济学动态，2018（8）：3 ～ 22.

[27] 德隆·阿西莫格鲁，詹姆斯·A·罗宾逊著.李增刚译.国家为什

么会失败[M].长沙：湖南科技出版社，2015：1 ～ 424.

【作者单位】1.中国财政科学研究院， 北京 100142;2.华夏新供给经济学研究院， 北京 100089