候答一分钟，智慧一百分

钱鸣

【摘  要】  美术的教学过程中，有种艺术叫留白，其实在常态的教学过程中，我们教师抛出问题以后，也需要留白，这种留白其实就是候答，在我们的课堂教学研究过程中，如何候答，候答什么？候答多久等都是一种教育艺术的体现。

【关键词】  候答;初中数学;智慧;策略

初中数学有其特定的学科特点和学科魅力，在初中数学的课堂教学过程中，我们的候答也有其特定的教育艺术和教育机智在其中。笔者就以初中数学的常态教学为例，谈谈如何通过课堂教学行为来达成候答艺术的升级，具体我们可以从以下几个环节着手。

一、优化问题设计

有了问题才能回答问题，因此要让候答艺术科学合理地服务于课堂教学行为，我们必须实现优化我们的问题设计，无论是课堂上教师结合具体教学问题设计的问题或问题链，还是教师为了达成某一教学目标而设置的问题链，我们都需要深入优化我们提出的问题。具体我们可以从以下三个环节来优化问题的设计。

1.锁定学情、精准提问。结合学生的基础和我们的教学内容，我们的问题一定要适合学生的思维生长，千万不能盲目提升，随机提问。而是结合学生的能力，巧妙化解问题，将一个主要解决的大问题化成几个小问题，一步一步引导学生去回答。

2.锁定难点、巧妙提问。问题要突破的关键是课堂教学的难点和重点，此时，我们需要解决学生的思维盲点，在这个过程中，我们需要缓解问题，我们需要结合难点，让问题一一突破。

3.迎合学生、注重追问。学生在候答的过程中肯定会遇到一定困难，为了让学生有一定的思维，并结合他们的候答现状，我们需要进一步追问学生，这种追问是一种变相的启发学生。

比如，在认识一元一次方程的教学过程中，我们为了让学生会判定一元一次方程，我们作以下提问：①2X+1=3;②y2-2y+1=0;③2a+b=3;④2-6y=1;⑤x=13是一元一次方程的有____，说说你的理由____？

在学生回答正确以后，我们再追问学生，你能总结判定方法吗？

问题的优化，配合候答的巧妙，学生在此过程的参与度远远超越我们的想象，效果也是显而易见的。

二、预设问题答案

在教学过程中，我们都需要预设我们活动开展以后可能出现的教学现象，并对相应的现象做好充分的准备。只有做好这方面的充分准备，我们才能在教学过程中锁定候答的时间，把握候答的火候。为此，在预设问题答案的过程中，我们需要从下面三个环节来预设。

1.预设正确答案，无论是抛出一道题目，还是课堂中的一个简单提问，我们都需要预设好正确的答案，这是备课所必需的第一条。

2.预设错误答案。这一个环节是直观重要的，学生是千变万化的，学生的思维也是海阔天空的，答案也就是千变万化，有些答案教师在教学过程中是可以预设或者及时驾驭的，但是有些答案没有充分预设的话，很多教师可能就会挂黑板，或者顺势忽悠过去，这是千万不可的。为此，我们要尽可能考虑全面、考虑充分。

3.预设应对策略。知己知彼百战百胜，在问题呈现以后，我们不仅需要预设学生可能出现的解答，也要预设好相应的应对策略，让学生充分思考后，得到充分的提升，也顺应教师的预设，巧妙地突破难点，建构新认知。

比如，以一元一次方程的应用教学为例，我们在教学活动结束后，布置如下一道例题来让学生思考，一方面，我们为了预设其效果，让答案更加丰富、更加具有进阶，我们这样设计。

例题2，一桶油连桶的重量为8千克，油用去一半后，连桶重量为4.5千克，桶内有油多少千克？设桶内原有油x千克，则可列出方程___________________。我们还可以设哪个量为未知数，你可以列出几种方程。

这样的开放性问题有其特定的价值和优势，但是也势必有其候答的空间，为了确保候答的价值，预设充分那是必须的。

三、循序候答空间

候答的过程是要求讲究艺术与智慧，教师在教学过程中要注重候答空间的循序渐进，在教学过程中，教师不仅要把时间给学生，更要把空间给学生，具体我们可以从以下三个环节着手。

第一步，把握学生候答的难度。教师要锁定好适合候答的内容和难度，即必须值得候，有候的价值，不能太简单，简单到很多学生不假思索答案就出来;更不能花太多的时间也候不出来。

第二步，提升学生候答的价值。这些候答的内容不仅仅是为了解决单一的问题，更是为了系统问题的解决，起到承上启下、继往开来的效果，有了这个问题的解决，学生提升的不仅仅是这个题目，更是系统知识的掌握或者某个重点、难点的突破。

第三步，还原学生候答的空间。在候答的过程中，一定要发挥小组合作的力量，启发学生全员参与到候答中，让集体的力量促进全员的思维跟进，全面提升候答的全员育人的价值。

比如，在专题复习《 三垂直全等模型》的过程中，笔者呈现这两道具有梯度的题目，以此促进隐性分层，全员候答的效果，确保每个学生都参与其中，又有循序渐进、分层提升的效果。

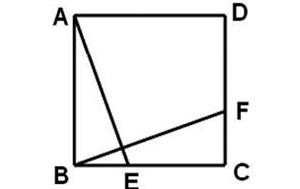
例题1，如图，正方形ABCD，BE=CF。   求证：（1）AE=BF;（2）AE⊥BF。

例题2，直线上有三个正方形a、b、c， 若a、c的面积分别是5和11，则b的面积是                     。

总之，在课堂教学中，候答是一种策略，也是教师教育机智的提升，更是凸显学生学习能力进阶提升的关键。教师需要不断深化候答的實践与研究，促进其价值的最大化。

【备注：本文系江苏省教育科学“十三五”规划专项课题《生态教育视域下初中课堂候答实践研究》的理论研究成果之一（E-b/2020/14）。】