繁忙高速铁路列车运行图结构优化研究

于汝滨，任 冲，闫海峰

YU Rubin1, REN Chong1, YAN Haifeng2

（1.中铁二院工程集团有限责任公司 交通与城市规划设计研究院，四川 成都 610031；2.西南交通大学 交通运输与物流学院，四川 成都 610031)

(1.Institute of Transportation and Urban Planning and Design, China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031, Sichuan, China; 2.School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, Sichuan, China)

随着高速铁路客流激增，国内外繁忙高速铁路干线能力紧张问题日渐凸显。以京沪高速铁路(北京南—上海虹桥)为例，2018年发送旅客1.96亿人次，全线日行车量108对/d，其中徐州东—蚌埠南区段高达157对/d，高峰小时列车平均运行间隔仅为5 min，高速铁路列车运行非常繁忙[1]。为了满足不断增长的客运需求，亟需优化繁忙高速铁路列车运行图的结构，提升区间通过能力。由于世界上典型的繁忙高速铁路较少，因而国内外针对繁忙高速铁路运行图优化的研究较少。同时，由于运行图结构的几何特性难以描述，运行图的结构指标与通过能力间的关系难以量化分析。既有运行图结构优化通常采用非线性规划建模[2-5]或建立评价体系并进行运行图仿真[6-8]，表达复杂，求解困难，不利于指导实际。繁忙高速铁路设施设备利用率高、列车间隔时间短，常规扩能措施并不适用。由于繁忙高速铁路行车量大、运行线铺画密集，考虑列车运行图中密铺运行线几何结构的敏感性，可以通过优化运行图结构来提升区间通过能力。因此，通过理论分析，明确运行图结构与通过能力间的定性关系，建立运行图结构与通过能力间的数量表达方法，并以此为基础，优化运行图结构，以提升通过能力。

1 繁忙高速铁路列车运行图结构分析

1.1 列车运行图结构

繁忙高速铁路干线(简称“繁忙高速铁路”)定义为：连接经济发达地区或经济大区，在路网中起重要骨干作用，全线日均行车量超过100对/d，繁忙区间行车量超过140对/d的高速铁路干线。根据最新世界各国铁路运营资料[1,9-13]，国内外繁忙高速铁路能力利用情况如表1所示。由表1可知，今世界繁忙高速铁路仅有6条。

繁忙高速铁路有以下特点：①行车量大，区间能力紧张；②跨线列车多且占比大，接入时间固定，运行调整困难，对能力有一定影响；③停站次数及越行限制多，停站产生的能力扣除是影响高速铁路通过能力的主要因素。繁忙高速铁路由于列车停站次数多、停站规律性差、越行组织复杂，加剧了该因素对通过能力的限制。

列车运行图结构指运行图上各类列车运行线的时空布局。当铁路信号、联锁、闭塞设备固定的前提下，铁路通过能力主要受到列车运行图结构的影响。从理论层面看，运行图结构即为运行线和停站间的协调。运行线间特定的结构可以降低运行图无效时间，从而提高区间通过能力，如“递远递停”铺图结构、利用作业停时组织越行等。分析京沪高速铁路运行数据，可以得出繁忙高速铁路运行图结构优化原则如下。

（1）同类列车成组铺画。成组铺画的追踪列数越多，每一列车占用运行图的时间越少，相应B类列车(低速动车组列车)对A类列车(高速动车组列车)的影响越小，可以铺画的总列数越多；除了同类列车外，停站方案相近列车也可邻近铺画。相似停站列车先后布置次序如图1所示。

（2）相邻列车“递远递停”。相邻列车停站顺序可以由远而近，也可以由近及远。A类列车“递远递停”停站方式如图2所示。2种方法对高速铁路通过能力的影响不同。图2中，a + b与c + d方式比较，后者的停站方案呈现阶梯式特点，可以更好地节约运行图能力。

（3）减少越行与待避的次数。A类列车不越行过多的B类列车（含停站多的A类车），以减少运行图的空费时间，B类列车待避次数不宜过多，否则将严重影响B类列车的旅行速度。

表1 国内外繁忙高速铁路能力利用情况Tab.1 Capacity utilization of the busy high-speed railway at home and abroad

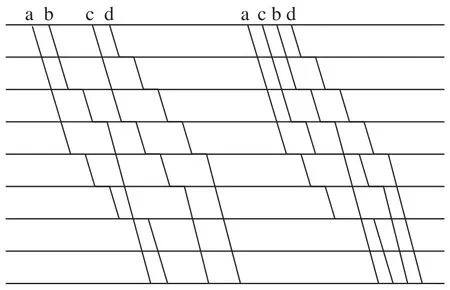
图1 相似停站列车先后布置次序Fig.1 Order of similar stop plan trains

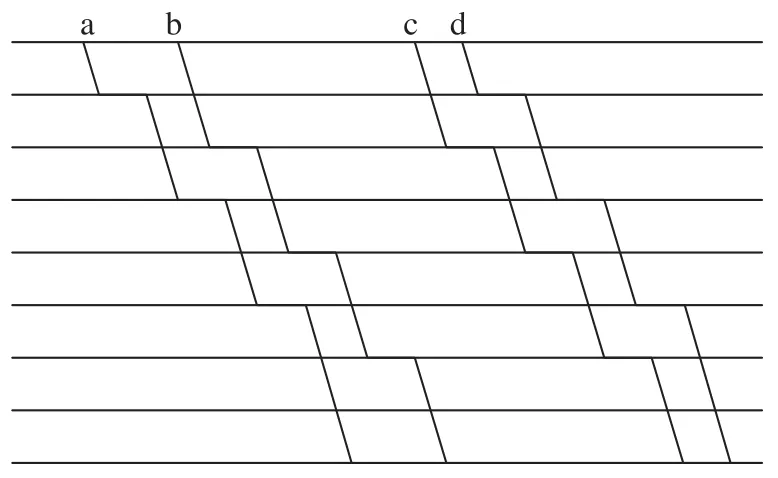
图2 A类列车“递远递停”停站方式Fig.2 A type trains’ stop plan diagram

根据上述特点，可以给出运行图结构的优化原则，在运行图的图解分析中，可以根据这些原则，设计运行图结构的评价指标。

1.2 列车运行图结构指标分析

1.2.1 运行线占用时间

运行线占用时间是通过能力的评价指标，可以用于量化运行图结构。在运行图统计区域中，对于任意车站i(i= 1，2，…，n)，第1条运行线在i站到达时刻(始发时刻)与最后一条运行线在i站出发时刻(终到时刻)之间的间隔时间，为i站的车站占用时间。统计区域中所有车站占用时间的最大值即为运行线占用时间(简称“占用时间”)，记为T运占(单位为min)，计算公式为

式中：为i站的车站占用时间，min；为统计的第1条运行线在i站的到达时刻，如果i为该运行线的始发站，则为始发时刻；为统计的最后一条运行线在i站的出发时刻，如果i为该运行线的终到站，则为终到时刻。

1.2.2 运行图结构指标

（1）列车停站方案数。在运行图中，如果列车区间运行速度相同，则占用时间取决于列车停站方案的数量。

（2）越行次数。对于繁忙高速铁路，每次越行均会出现前方列车停站等待后方列车的情况，从而使占用时间增加。

（3）区间群数。对于一个列车运行区段，相同停站方案运行线相邻密铺可以最大程度地减少空费时间。为了统计运行图这一结构特点，定义区间群数指标。自运行图某一时刻开始按时间顺序统计，将首条运行线记为i，其相邻运行线i+1如果与i的停站方案完全相同，则记i与i+1属于同一个群I1；继续向右搜索i+2，i+3，…，i+n，直到找出与i停站方案不同的列车i+k，将i至i+k-1记入到群I1中，群I1饱和；将i+k-1与i+k记入群I2并继续搜索，直至搜索时间域的时长达到设定阈值的上限。此时，搜索时间域内互不包含的群Ix的个数称为群数。某一区间内的群数简称为区间群数(单位为组)。区间群数统计示例如图3所示。①②③区间两端车站停站方案一致，可以归为一个群；③④相邻，但停站方案不一致，可以归为一个群；同理，④⑤，⑤⑥各为一个群。因此，图3的运行图中，区间群数为4。由图3可知，区间群数反映的是运行图中相同列车连发的车组数。

图3 区间群数统计示例Fig.3 Statistical examples for the interval groups

（4）运行图四边形平均面积。为统计相同停站方案运行线是否相邻密铺，引入运行图四边形平均面积概念，与区间群数指标进行比较分析。运行图四边形、运行线距离统计示例如图4所示。运行图中任意纵向相邻2条运行线与横向相邻车站间距线共同构成一个“四边形”，如图4中①—⑧均为四边形，每个小四边形的面积为1。其中，具有相同停站方案的相邻运行线间四边形个数为1（①②、③④可分别合记为一个大的四边形）。运行图中小四边形的总面积除以四边形的总个数，即可以得到运行图四边形平均面积，简称“四边形平均面积”。四边形平均面积与区间群数一样反映了相同列车连发车组数。

图4 运行图四边形、运行线距离统计示例Fig.4 Statistical examples for the quadrilateral and running line distance of the train diagram

（5）运行线距离。对于某一车站，2条相邻运行线采用同一停站方案可以减少占用时间。为统计该特性，参考信息编码中的“海明距离”，引入“运行线距离”。运行图中相邻2条运行线因停站方案不同而存在停站差异的车站数量称为运行线距离。如图4中，A，B示例在车站2的运行线距离为0；C，D示例车站2运行线距离为1。

2 列车运行图结构指标计算与优化

2.1 列车运行图铺画步骤

以京沪高速铁路若干客运区段为研究对象，在给定不同列车开行方案条件下，批量铺画列车运行图。图解方案采用京沪高速铁路的标尺，铺图方法为随机铺画，即大部分列车严格按照京沪线标尺紧密铺画，小部分列车通过固定停站率，调整区间均衡性。在保证停站率不变的前提下，合理铺画运行线，要求不同停站方案的列车均匀分布在各个时段，避免所有列车都是集中连发的情况出现。为方便研究，仅铺画下行方向运行线，假设列车的技术速度相同，不允许压缩运行图的缓冲时间。依据运行图铺画结果[1]，运行图的铺图步骤如下。

步骤1：选取实际运行图作为参照。根据2019年上半年京沪高速铁路列车运行图统计资料[2]，最繁忙区段(徐州东—蚌埠南)的高峰时段(10 : 00—11 : 30)铺画20对列车，考虑本线上、下行运行线结构具有对称性，选取徐州东—蚌埠南区段高峰时段(10 : 00—11 : 30)下行方向作为研究对象。

步骤2：选定列车运行区段为滕州东—定远段（含徐州东—蚌埠南），虽然徐州东—蚌埠南为最繁忙区段，但是为了便于铺图研究徐州东、蚌埠南2个车站的停站方案，将此区段向两端延长至滕州东及定远，能直观体现徐州东—蚌埠南的停站方案。

步骤3：设定最小追踪间隔时间为3 min，铺画20列下行动车组列车。

步骤4：京沪高速铁路区段各站的列车停站率和越行率取值如表2所示。按表2数据铺画运行图，并尽可能减少停站方案的数量。

表2 区段各站的列车停站率和越行率取值 %Tab.2 Values of train stop rate and overtaking rate of each station in the section

步骤5：将直达和停站列车分别成组铺画。

步骤6：将具有相同停站方案的列车成组铺画。

步骤7：根据“递远递停”的原则，调整各列车组间的前后顺序。

步骤8：调整开行方案，直达列车应均匀铺画，高峰时段增加列车停站，低峰时减少列车停站；不同停站方案列车交错开行，合理安排越行[14]。

按上述运行图铺画步骤，铺画得到70张列车运行图，均计入统计样本集。

2.2 列车运行图结构指标计算

（1）运行线占用时间。统计铺图样本集中的运行图，可以得到运行线占用时间分布如图5所示。由图5可知，运行线占用时间在86 ～ 193 min之间，平均占用时间约114 min，标准差19.5 min。由占用时间的统计结果可知，在相同行车量下(20对)，随着占用时间的增大，列车占用的运行图能力随之增大。当列车运行图被占用率达到100%时，样本运行图能力无富余，运行线占用时间与运行图被占用能力的关系如图6所示。占用时间与被占用能力百分比基本呈线性正相关。占用时间为90 min时，能力占用为78.9%；占用时间升至114 min时，能力占用达100%。由图6可知，运行线占用时间与能力利用率存在明显的相关关系，可以将占用时间作为评价运行图能力利用率的指标，以定量地评价运行图结构的优劣。

图5 运行线占用时间分布Fig.5 Train path occupied time distribution

图6 运行线占用时间与运行图被占用能力的关系Fig.6 Relationship between occupied time and occupied capacity of train diagram

（2）列车停站方案数。停站方案数与占用时间的关系如图7所示。由图7可知，列车停站方案数与占用时间相关性较弱。

（3）越行次数。越行次数与占用时间的关系如图8所示。由图8可知，越行次数与占用时间的相关性较弱。

（4）区间群数。区间群数与占用时间的关系如图9所示。由图9可知，区间群数与占用时间呈正相关关系。

图7 停站方案数与占用时间的关系Fig.7 Relationship between the number of stop plans and occupation time

图8 越行次数与占用时间的关系Fig.8 Relationship between the frequency of overtaking and occupation time

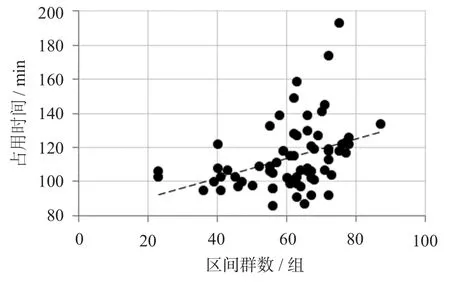
图9 区间群数与占用时间的关系Fig.9 Relationship between the interval groups and occupation time

（5）运行图四边形平均面积。四边形平均面积与占用时间的关系如图10所示。由图10可知，四边形平均面积与占用时间呈负相关。

（6）运行线距离。运行线距离与占用时间的关系如图11所示。由图11可知，运行线距离与占用时间呈正相关。

2.3 运行图结构与通过能力关系分析

图10 四边形平均面积与占用时间的关系Fig.10 Relationship between the average area of quadrilateral and occupation time

图11 运行线距离与占用时间的关系Fig.11 Relationship between the train line distance and occupation time

根据运行图结构指标与占用时间关系分析可知，区间群数与占用时间相关性最强，即对应区间群数对线路通过能力影响最大。但是，研究[1]发现区间群数、四边形平均面积等5个评价指标之间也具有相关性，且无法完全剔除。因此，为了分析区间群数变化对占用时间的影响，制订适用的控制变量法：根据评价指标间相关性，将区间群数分段，各分段中区间群数变化的同时，控制四边形平均面积、运行线距离、越行次数、停站方案数等其余评价指标在一个较小的范围内波动，从而减少这些变量对数量关系的影响。由此方法筛选样本，可以得到控制变量法下样本集筛选结果如表3所示。

通过曲线拟合，得到控制变量下样本集区间群数与占用时间的关系如图12所示。图12为区间群数所描述的运行图结构与区间通过能力之间数量关系。由图12可知，区间群数与占用时间基本服从正指数函数分布，当每20列车的区间群数增至19组时，京沪高速铁路通过能力被完全占用。

2.4 运行图结构优化

以上研究表明，区间群数是区间通过能力的强相关指标，可以用于描述运行图结构与区间通过能力之间的数量关系，而四边形平均面积、运行线距离、越行次数、停站方案数等指标与区间通过能力的相关性较弱。因此，以京沪高速铁路为例，利用以上方法分析高峰时段繁忙区段的列车运行图结构对通过能力的影响。京沪高速铁路徐州东—蚌埠南单位时间列车运行图(优化前)如图13所示。

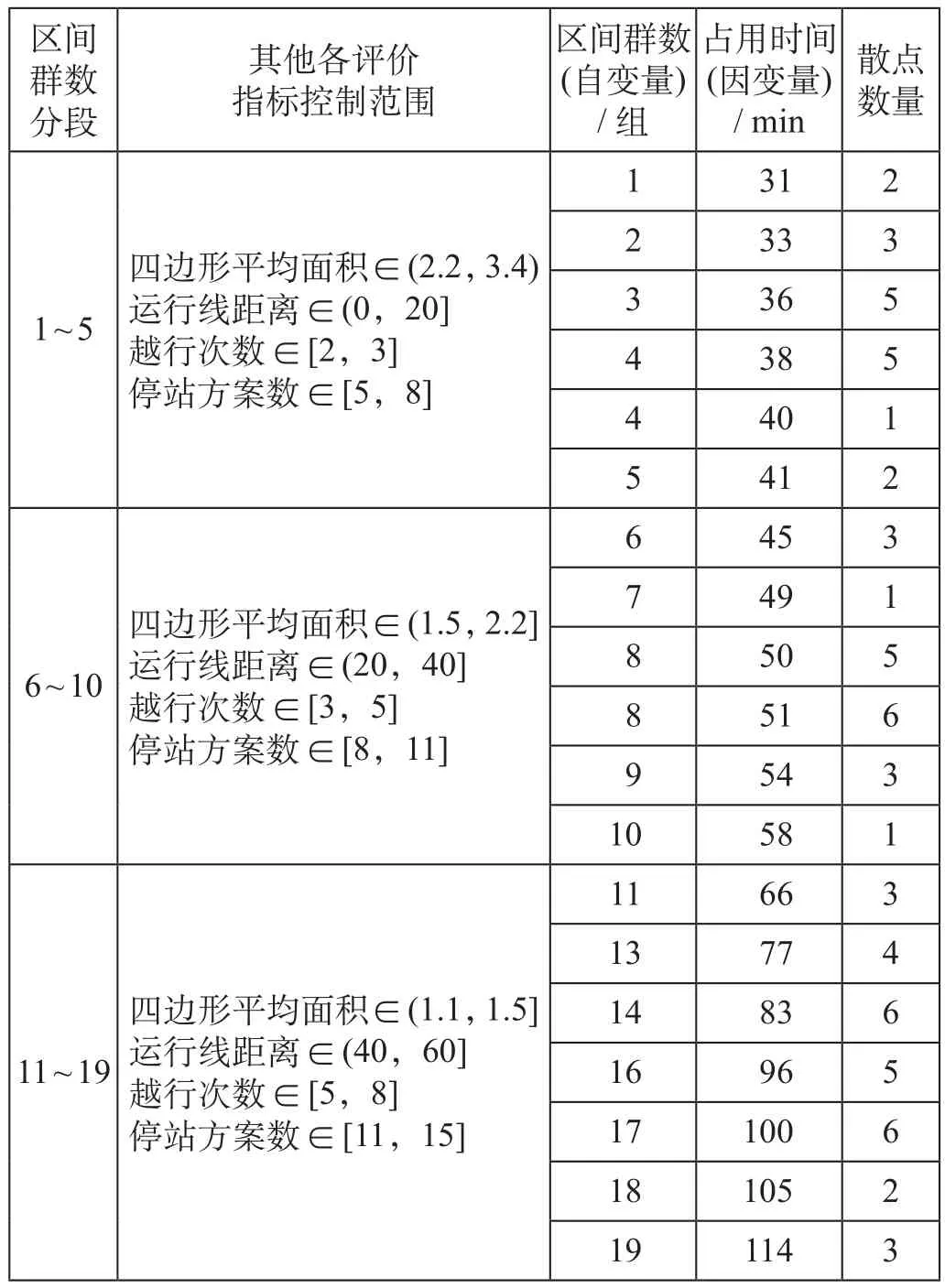
表3 控制变量法下样本集筛选结果Tab.3 Sample set chosen result under the control variable method

图12 控制变量下区间群数与占用时间的关系Fig.12 Relationship between the interval groups and occupation time after the variable is controlled

图13 京沪高速铁路徐州东—蚌埠南单位时间列车运行图(优化前)Fig.13 Train diagram of unit time of Xuzhou East-Bengbu South section of Beijing-Shanghai high speed railway before the optimization

由图13可知，选取京沪高速铁路高峰时段繁忙区段共包含20列下行列车。统计这20条运行线对应的区间群数为16组，在徐州东站的占用时间为98 min，区间群数和占用时间均有优化空间。根据列车运行图图解铺画步骤，以区间群数为评价指标，设计运行图结构优化算法，并选取徐州东—蚌埠南区段设计算例，具体实现步骤如下。

步骤1：缩减列车停站时间。设置京沪高速铁路旅客乘降标准时间为2 min (北京南、上海虹桥站除外)，设置徐州东—蚌埠南区段部分列车停站时间为 3 ～ 5 min。

步骤2：成组铺画相同停站方案列车。徐州东—蚌埠南段列车停站方案如表4所示。按照表4中的停站方案，成组铺画相同停站方案的列车，得到运行图初始方案。

表4 徐州东—蚌埠南段列车停站方案Tab.5 Train stop plans of Xuzhou East-Bengbu South

步骤3：调整运行图结构。通过逐站微调运行线布局，使停站、不停站列车大体呈交错分布，避免同种列车过度集中到发，并保证一定的运行图冗余时间，使运行图的结构更加合理。

步骤4：调整运行线顺序。在运行线交错分布的基础上，相邻运行线按“递远递停”原则调整，以减小占用时间。

步骤5：判断占用时间是否小于优化前占用时间98 min。如果是，则更新储存运行图方案，再选取1条京沪实际运行线增铺至图中，并返回步骤3；如果否，则输出运行图结果并统计占用时间和区间群数。

通过算法I得京沪高速铁路徐州东—蚌埠南段单位时间列车运行图(优化后)如图14所示。对比优化前后的运行图，可以得到徐州东—蚌埠南段运行图优化前后占用时间比较如表5所示。由表5可知，在列车对数相同条件下，优化后运行图占用时间缩短14 min；占用时间同为98 min条件下，优化后运行图可以增加3对列车。因此，经结构优化京沪高速铁路高峰时段(10 : 00—11 : 30)最繁忙区间(徐州东—蚌埠南)通过能力可以达到23对，较现行方案增加3对。

此外，本算例计算的是京沪高速铁路最繁忙区段的高峰时段，为了进一步提升该区段通过能力，铺画得到的运行图中预留的冗余时间很少。而对于通过能力相对富余的非高峰时段，还可以合理调整运行图结构，保证一定的运行图冗余时间。

3 结束语

繁忙高速铁路连接经济发达地区或经济大区，在路网中起重要骨干作用。优化繁忙高速铁路的运行图结构，对于提升高速铁路能力利用率，为旅客提供更加高效率的运输服务具有重要意义。利用图解法模拟铺画运行图，引入通过能力等价指标和运行图结构指标，可以较为准确、全面地对列车运行图的结构进行定量分析。利用该方法对现行京沪高速铁路列车运行图结构进行分析，结果表明京沪高速铁路的列车运行图结构存在优化空间，可以通过优化列车运行图结构，进一步提高线路的通过能力。

图14 京沪高速铁路徐州东—蚌埠南段单位时间列车运行图(优化后)Fig.14 Train diagram of unit time of Xuzhou East-Bengbu South section of Beijing-Shanghai high speed railway after the optimization

表5 徐州东—蚌埠南段运行图优化前后占用时间比较Tab.5 Comparison of occupation time before and after the optimization of Xuzhou East-Bengbu South train diagram