考虑席位类型的旅客列车开行方案优化研究
2020-12-28姜春阳杨信丰
姜春阳,杨信丰,李 涛
JIANG Chunyang, YANG Xinfeng, LI Tao
(兰州交通大学 交通运输学院,甘肃 兰州 730070)
(School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou 730070, Gansu, China)
0 引言
随着铁路运输的飞速发展,越来越多的旅客选择铁路出行,旅客出行需求多样化,对乘车过程中的舒适性有了更高要求。硬卧席位性价比较高,旅客选择较多;硬座席位舒适度较差但价格较低,适合部分旅客尤其是短途旅客;软卧席位拥有较高的舒适度和价格,旅客选择相对较少。铁路部门在制定开行方案时,考虑旅客对各类席位的需求以及旅客需求对列车编组的影响,有利于提升旅客对铁路运输服务的满意度,高效完成旅客运输任务,增加铁路运输部门的收益。
目前,国内外学者针对旅客列车开行方案优化问题和铁路席位管理问题做了大量的研究。黄鉴[1]首先分别建立了客流预测模型与开行方案优化模型,再将其综合优化,模型以运输收益最大化和列车运行路径广义阻抗最小化为目标函数。魏文萍等[2]根据不同的消费水平将客流划分为3个层次,以预测的客运量为基础,制定合理的列车开行方案。张博等[3]引入非集计理论的Logit 模型分析旅客的乘车选择行为,在此基础上建立高速铁路列车开行方案优化模型。诺敏[4]和龙品秀等[5]分别从节假日和不同需求日对旅客列车开行方案进行优化,建立不同需求的开行方案,提高不同需求的旅客满意度。Chew等[6]、Schon[7]以及Sato等[8]建立了离散时间条件下的动态规划模型,使用多项Logit模型来描述客户的离散选择。宋晓芳[9]提出针对单趟车的票额分配方法及动态调整策略,解决单线路多区段的供需匹配问题。Hetrakul等[10]综合考虑了定价和座位分配,提出用多项式Logit和潜在类模型的离散选择方法来描述铁路旅客购票情况。包云[11]和骆泳吉[12]构建了多等级票价下多列车席位控制模型,设计了列生成算法进行求解。苏云汉[13]针对席位管理策略,分析铁路动态嵌套席位存量控制策略后,提出了速度更快、原理更简单的最优席位选择法。
现有文献大多以客流动态变化的情况优化列车开行方案,从铁路运输企业和旅客2个方面考虑建立多目标优化模型,但在旅客对席位类型的需求特性以及列车不同席位类型的编组对于客流的吸引方面研究较少。因此,将旅客对不同席位类型的需求及不同席位的列车编组方案纳入开行方案设计考虑因素,以满足旅客多样化的选择需求。
1 考虑席位类型的旅客列车开行方案模型设计
1.1 模型相关设置
以普速铁路旅客列车为研究对象,旅客列车分类定义为列车类型k,k= 1代表直达特快列车,k= 2代表特快列车,k= 3代表快速列车。普速旅客列车的席位可分为硬座、硬卧、软座和软卧4种,将软座和硬座统一归于硬座席位,旅客列车的席位分类为席位类型w,w= 1代表硬座,w= 2代表硬卧,w= 3代表软卧。
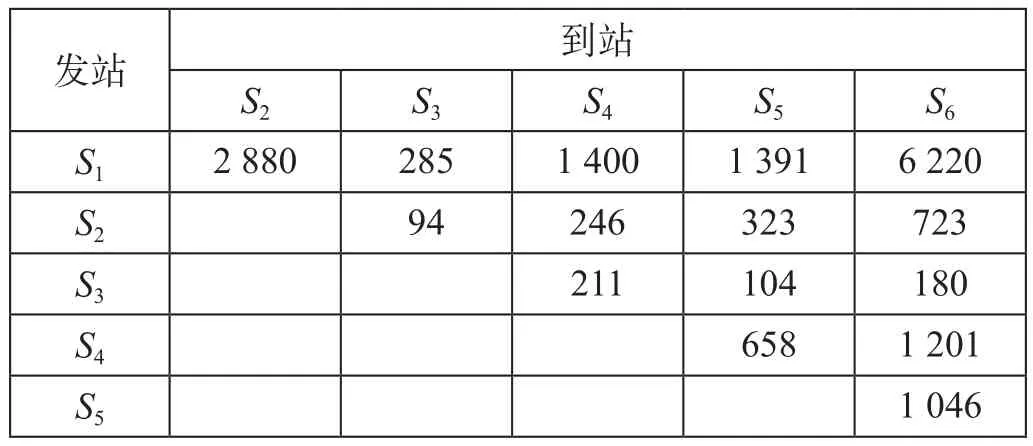
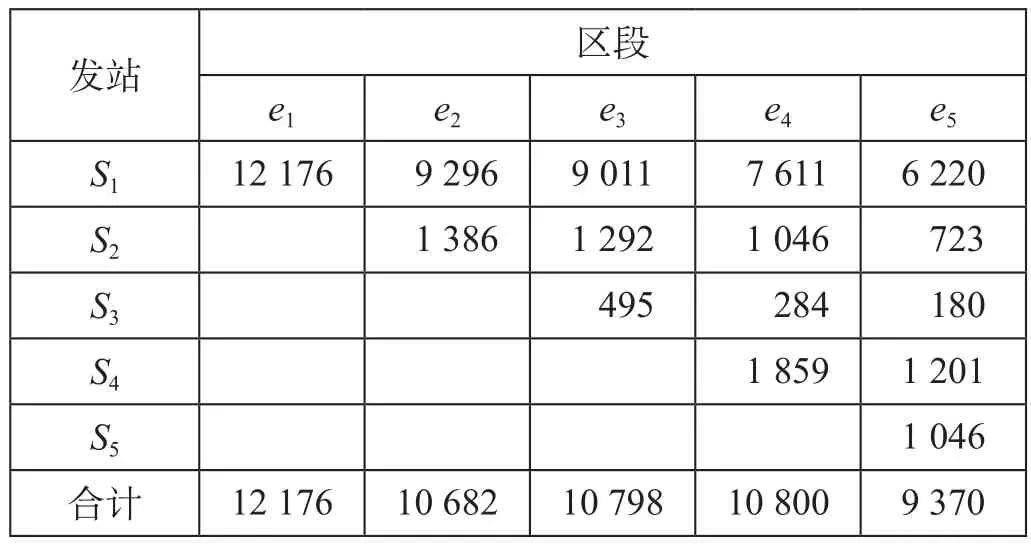
定义各变量如下。S= {s1,s2,…,sn}为所有车站的集合,si为车站标识,si∈S;SO∈S为始发站的车站集合,SD∈S为终到站的车站集合;sa为始发站且sa∈SO,sb为终到站且sb∈SD,a 旅客出行会根据出行距离、消费观念、列车特性等因素,选择不同的席位类型。制订合理的开行方案,考虑旅客多样化的选择需求,各类列车灵活编组,满足铁路运输收益最大化和未满足理想席位类型的旅客数量以及各类席位虚糜数量最小化。 (1)铁路运输收益最大化。铁路运输的运营成本一般可分为变动成本和固定成本。变动成本可以用车公里消耗和停站成本所表示。固定成本在通过能力范围内不会随运量的变化而变化,因此对于列车开行方案的影响较小。不同的席位车辆的“旅客列车服务”中的各项成本也有所不同,不同编组内容的列车成本也有所差异。不考虑固定成本,旅客列车开行成本的计算公式为 旅客列车运营收入即为旅客的票价支出,计算公式为 因此,旅客列车运输收益最大化的目标函数为 (2)未满足理想席位类型的旅客数量以及各类席位虚糜数量最小化。未满足理想席位类型的旅客数量以及各类席位虚糜数量最小化目标函数为 (1)列车停站约束。列车停站方案划分为大站停、交错停和站站停3种基本模式,列车具体停站方案应满足不同车站的停站要求。对于车站si∈S,将车站si的等级记作Ti,Ti= 1,2分别表示大站和小站,将k类列车的停站模式记作Γk,Γk= 1,2,3,分别表示大站停、交错停和站站停[1]。则此约束为 由公式 ⑸ 和 ⑹ 可知,当Ti>Γk时,yik= 0,即列车在比其停站等级低的车站不停靠;当Ti<Γk时,yik= 1,即列车在比其停站等级高的车站必然停靠;当Ti=Γk时,yik= 0,即列车在与其停站等级相当的车站可选择性停靠。 (2)上座率约束。模型必须满足各类席位的上座率达到一定的要求,即各类席位的席位利用率保持在一定的范围内。当各类席位上座率满足下限时,可以保证铁路部门的收益;当各类席位上座率达到上限时,可以为旅客提供更多的服务,提高旅客对于铁路运输的满意度。假设上座率的下上限分别为β1,β2,则此约束为 同时此约束也对目标函数中的公式 ⑷ 进行约束,各类席位虚糜数量最小化且保证上座率不能低于上座率的下限β1,也不能超过上座率的上限β2。考虑铁路部门的收益及我国铁路运营现状,上座率的下限β1取0.75;铁路运输会出现列车超员现象,为保证运输服务的质量,上座率的上限β2取1.1。 (3)客流需求约束。各个区段的旅客列车开行对数应该满足客流需求,即各个区段开行列车的载客容量应该大于等于客流需求,则此约束为 任意两站之间不同席位旅客选择所有列车类型的总人数应不大于这两站之间的旅客需求,约束为 (4)列车编组约束。各类列车的编组应符合相应的规定要求,假设各类列车编组的下上限分别为γ1,γ2,根据规定要求列车编组的下上限分别取13和20。此约束表达为 (5)客流量相互关联约束。该约束表达为 定员相互关联约束表达为 列车编组相互关联约束表达为 考虑席位类型的旅客列车开行方案的多目标优化模型是一个非线性多目标混合整数规划问题,该模型被公认为是极其困难求解的优化问题之一[14],这里采用遗传算法求解,核心思想是计算种群中个体的适应度,对适应度函数值的高低进行优胜劣汰,不断繁衍后代。遗传算法的优点在于全局收敛性较好,可以在较短的时间里得到满意解。 (1)染色体编码。染色体编码采用实数编码的方式。例如,Q1-6:[x1,x2,x3]表示始发站1、终到站6分别开行直达特快、特快和快速列车的数量;W1-6:[y1,y2,y3]表示始发站1、终到站6分别开行直达特快、特快和快速列车的停站方案;表示始发站1、终到站6开行直达特快列车的每辆车上硬座、硬卧和软卧的编组辆数。染色体编码示意图如图1所示。 图1 染色体编码示意图Fig.1 Schematic diagram of chromosome coding (2)计算适应度。计算时先统一量纲,将目标函数规范化。首先,求出目标函数C铁路的最大值和最小值然后,求出目标函数Q未的最大值和最小值最后,得规范化函数 根据规范化的函数,2个目标函数分别是求最大值和最小值,先将求最小值的目标函数取相反数,再线性处理双目标函数,设计适应度函数,则函数表达式为 式中:Z为个体的适应度函数值;δ为2个目标函数达到期望目标值的权重系数。 为了同时满足旅客和铁路部门的期望目标值,设δ= 0.5,记录该列车开行方案下的适应度值。 (3)选择算子。文中使用轮盘赌法选取新种群,对所有适应度函数求和作为分母,每个个体的适应度函数作为分子,得到的比值即为该个体被选中的概率,则公式表达式为 式中:Pi为个体i被选中的概率;Zi为个体i的适应度函数值,由公式(14-16)计算;M为种群大小。 遗传算法流程图如图2所示。 图2 遗传算法流程图Fig.2 Flow chart of genetic algorithm 算法步骤如下。 步骤1:设置列车运行区段和各类列车的相关参数取值。 步骤2:根据各类列车分担率和列车区段,固定列车编组产生初始种群。 步骤3:计算个体适应度函数值。 步骤4:根据轮盘赌法选择新种群。 步骤5:对新种群进行交叉、变异操作。 步骤6:判断最优适应度值是否发生变化。如果否,则停止当前运算,输出开行各类列车数量和停站方案的最优解且转到步骤7;如果是,转到步骤3。 步骤7:根据得到的各类列车的数量、停站方案和初始固定列车编组辆数,将该过渡方案作为初始染色体。 步骤8:计算个体适应度函数值,并根据轮盘赌法对个体进行选择,得到新的种群。 步骤9:对该条件下的新种群进行交叉、变异操作。 步骤10:判断最优适应度值是否发生变化。如果否,则停止当前运算,输出各类列车不同席位的编组辆数;如果是,转到步骤8。 (1)普速铁路网络假设。假设算例中普速铁路线沿途有6个车站,各车站均为大站,客流量较大,因此各类列车均站站停。普速铁路网络案例如图3所示。 (2)输送客流量假设。假设各车站间的日均输送客流量如表1所示。 (3)票价率设置。各类席位的票价率如表2所示。 (4)车公里费用、列车停站成本及各类席位的标准辆成本设置。各类列车的车公里费用如表3所示。 列车停站成本f停站= 1 000元 各类席位的标准辆成本如表4所示[15]。 (5)旅客列车车厢定员设置。各类席位的车厢定员如表5所示。 (1)多列车多席位旅客选择行为分析。根据既有客票数据分析旅客在不同列车不同席位等级之间的选择,主要考察经济性和旅行时间2个影响因素。运用多项Logit模型计算旅客选择各类列车的概率。旅客选择的广义成本效用函数[16]用Uk表示。 表1 各车站间的日均输送客流量 人Tab.1 Average daily passenger flow between the various stations 表2 各类席位的票价率 元/人公里Tab.2 Passenger-kilometer fare rate for various seat class 表3 各类列车的车公里费用 元/车公里Tab.3 Vehicle kilometer costs for various trains 表4 各类席位的标准辆成本 元Tab.4 Standard vehicle cost of various seats 表5 各类席位的车厢定员 人Tab.5 Various types of cabin seats capacity 式中:Ck为k类列车的直接费用成本,元;Tk为k类列车的旅行时间,h;B2,B3表示各自的系数;B1为常数项。 文中各类列车的直接费用的相关数据取各类列车的车公里费用进行计算[17],各类列车的旅行时间根据我国各类列车运行时速进行换算[18]。各类列车的相关数据如表6所示。 图3 普速铁路网络案例Fig.3 Case study of conventional railway network 表6 各类列车的相关数据Tab.6 Relevant data of various trains 计算过程中,常数项B1取0;各自的系数B2,B3均取1;为了统一数量级,旅行时间均按照列车运行100 km所花费的时间进行计算;用区间缩放法对2个影响因素做无量纲化的处理。 旅客选择k类列车的概率用Pk表示[17]。 区间缩放法的公式表达为 根据旅客选择行为的多项Logit模型,计算旅客选择各类列车的概率。各类列车的广义成本及分担率的计算结果如表7所示。 表7 各类列车的广义成本及分担率的计算结果Tab.7 Calculation results of generalized cost and share rate of various trains 利用表7各类列车分担率的计算结果,可以作为决策变量k类列车的数量Xk的参考指标。 根据不同类列车车厢编组的实际情况,以及调查研究客流需求情况[9],得到各类列车不同席位类型的车厢编组比例如表8所示。 表8 各类列车不同席位类型的车厢编组比例 %Tab.8 Car formation of different types of seat of various trains 利用表8各类列车不同席位类型的车厢编组比例,计算k类列车中每列车上w类席位的编组辆数Nkw。 (2)初始方案。由表1各车站间的日均输送客流量计算出各区段客流密度情况。两站之间的客流密度就是所有利用了该区段的客流之和。因此,各区段客流密度如表9所示。 表9 各区段客流密度 人Tab.9 Passenger flow density in each section 根据表7各类列车的分担率得出乘坐各类列车的客流量,依照“按流开车”的基本原则[16],得到列车初始开行方案示意图如图4所示。初始开行方案下客流密度与客运能力比较表如表10所示。 区段S1—S6中开行4列直达特快列车、3列特快列车和1列快速列车;区段S1—S5中开行1列特快列车;区段S1—S2中开行1列快速列车。其中,每列直达特快的车厢编组为3节硬座、11节硬卧和2节软卧,直达特快的定员为1 152人;每列特快列车的车厢编组为5节硬座、9节硬卧和1节软卧,特快列车的定员为1 220人;每列快速列车的车厢编组为5节硬座、10节硬卧和1节软卧,快速列车的定员为1 286人。 (3)优化方案。计算求得的列车近似最优开行方案示意图如图5所示。根据求得的近似最优开行方案以及表8各类列车不同席位类型的车厢编组比例和各席位车厢定员,得出各区段不同类列车的编组情况如表11所示。近似最优开行方案下客流密度与客运能力比较表如表12所示。优化后的开行方案任何区段的客运能力均能满足客流密度。 图4 列车初始开行方案示意图Fig.4 Schematic diagram of initial train operation scheme 表10 初始开行方案下客流密度与客运能力比较表 人Tab.10 Comparison table of passenger flow density and passenger capacity under initial operation scheme 从算例结果可以看出,优化后所得开行方案与初始开行方案相比,优化后所得的开行方案不仅可以满足更多客流对不同席位类型的需求,而且能够提高列车中各类席位的上座率、减少列车能力虚糜。同时,优化后的开行方案采用不同列车灵活编组,与固定的列车编组相比,提高了列车上座率。优化方案可以在保证铁路运输收益的前提下,满足旅客多样化的选择需求,提升旅客对铁路运输服务的满意度。 通过对考虑席位类型的旅客列车开行方案的研究,较全面地满足了旅客出行的不同需求,建立了考虑席位类型的旅客列车开行方案的优化模型,设计遗传算法对模型进行求解,得到以下研究结论。 图5 列车近似最优开行方案示意图Fig.5 Schematic diagram of the approximate optimal train operation plan 表11 各区段不同类列车的编组情况 辆Tab.11 Formation of different kinds of trains in each section 表12 近似最优开行方案下客流密度与客运能力比较表 人Tab.12 Comparison table of passenger flow density and passenger capacity under approximate optimal operation scheme (1)考虑到旅客对不同席位需求的同时,兼顾了铁路部门的收益情况。所得方案不仅可以保证铁路部门的收益,而且可以较好地满足旅客的乘车选择需求。 (2)运用Logit模型对选择直达特快列车、特快列车和快速列车3类列车客流之间的分担率进行预估。 (3)在设计算法时,构造适应度函数时对2个目标函数进行线性加权处理,并对目标函数未满足理想席位类型的旅客数量以及各类席位虚糜数量最小化做相反数处理,最终计算得到较优的考虑席位类型的旅客列车开行方案。 (4)在一定的假设条件下建立模型,可能与实际问题有偏差,如缺乏旅客对于不同席位选择因素的研究、车站通过能力以及区间通过能力约束的考虑等,后期将对其进行研究,完善考虑席位类型的旅客列车开行方案的优化。1.2 目标函数




1.3 约束条件
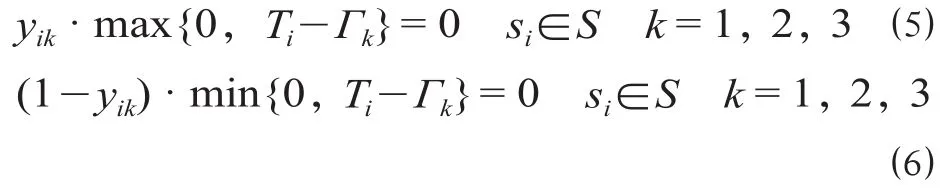
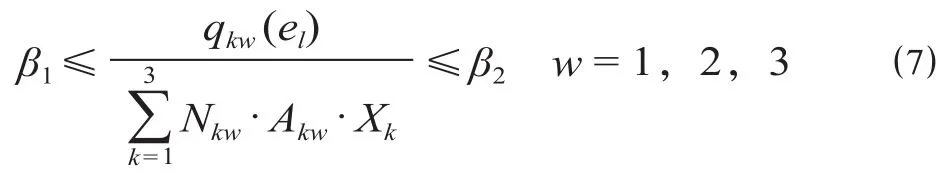






2 考虑席位类型的旅客列车开行方案多目标优化模型求解算法
2.1 遗传算法关键步骤



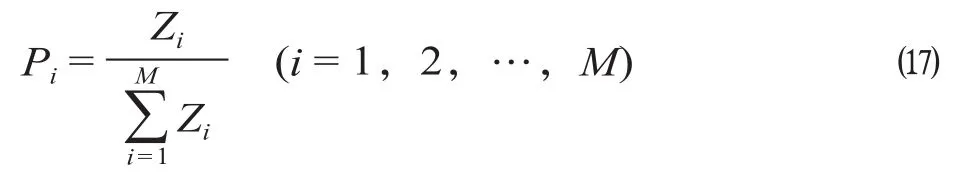
2.2 算法流程

3 算例分析
3.1 算例假设
3.2 算例求解








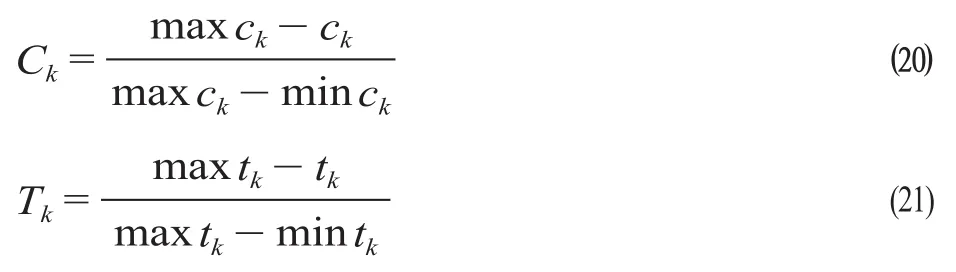




4 研究结论



