时变扩散系数对混凝土结构服役寿命的影响

蒋琼明, 吉学宽, 农忠霖

(1.广西大学土木建筑工程学院， 南宁 530004； 2.北部湾大学建筑工程学院， 钦州 535011)

混凝土氯离子扩散系数是影响氯盐环境下混凝土结构的耐久性能的一个重要材料参数，因此扩散系数模型的准确性直接影响着混凝土结构服役寿命预测的准确性。混凝土氯离子扩散系数的大小与混凝土材料内部的孔隙率及孔隙特征直接相关，会随着混凝土水化过程的进行而不断衰减，表现出时变性。通常采用浸泡实验[1-5]和电场加速实验[5-9]，通过数据拟合衰减系数来量化表示扩散系数的衰减快慢。Song等[10]通过Monte Carlo抽样(MCS)方法对混凝土海底隧道的可靠度进行了计算，并重点分析了氯离子扩散系数的时变性对混凝土结构服役寿命的影响；杨绿峰[11]建立摄动随机有限元法研究了氯离子扩散系数的时变性对氯离子扩散过程的影响；徐彧[12]针对各地区海工混凝土暴露不同时间的2 481 组混凝土氯离子表观扩散系数数据(最长达97 a)，系统研究了时变性对不同暴露地区氯离子扩散系数的影响。研究表明氯离子扩散系数的时变性能明显减缓氯离子侵入混凝土的速度，有效延长了混凝土结构的服役寿命[10-12]。

然而，由于混凝土氯离子扩散系数及其衰减系数既与混凝土材料本身有关[12]，又受实验过程的影响，所以衰减系数与氯离子扩散系数一样具有随机性[13]，相关研究中对混凝土氯离子扩散衰减系数的随机特性进行了讨论[14]，并同时考虑氯离子扩散系数及衰减系数的随机性，通过MCS方法对氯盐环境下混凝土结构中钢筋的耐久性可靠度进行了计算分析[15]。

参数敏感性是结构可靠度分析的一个重要组成部分，可以据此确定模型中不同参数及其变异性对结构可靠度的影响程度[16]。Saassouh等[17]利用重要性因子反映随机变量变异性对混凝土结构耐久性可靠度的影响，但该重要性因子不能反映随机变量均值对可靠度的影响，且未考虑氯离子扩散系数的是时变性及其随机性。Hohenbichle等[18]分别利用可靠指标对随机变量均值和标准差的偏导数定义结构可靠度对随机变量均值和标准差的敏感系数，但这两个参数带有量纲，容易受到工程结构中不同参数量纲的影响，因此不能准确反映随机量对结构可靠度的敏感性。为此，Mansour等[19]将Hohenbichle等[18]定义的敏感系数乘以随机变量标准差，使之无量纲化。但该敏感系数纯粹为了满足无量纲化的需要而建立，其物理意义缺少合理解释，难以正确反映随机变量对可靠度的影响程度。

考虑混凝土氯离子扩散系数衰减系数的随机性，结合一次二阶矩法，建立了基于氯离子二维扩散的混凝土结构服役寿命可靠度分析模型，据此计算氯盐环境下混凝土结构基于正常使用极限状态的可靠度及其服役寿命。根据全微分公式导出可靠度对随机变量均值和变异性的无量纲敏感系数，克服了传统的可靠度敏感系数的缺陷，并据此研究了氯离子扩散系数衰减系数对结构耐久性的影响。计算结果表明，混凝土氯离子扩散衰减系数及其随机性和混凝土保护层厚度对氯盐侵蚀下混凝土结构耐久性的影响占主导地位。

1 混凝土氯离子扩散时变模型

混凝土水化是一个缓慢的过程，随着水化的不断进行，混凝土的孔结构会得到逐步改善，从而使氯离子扩散系数逐渐减小，因此认为氯离子扩散系数是具有时变衰减性的。测量混凝土结构的氯离子扩散系数衰减模型一般有浸泡实验[1-5]和电场加速实验[5-9]两类实验方法。通过这两类实验通常得到的扩散系数模型分别为氯离子扩散时间(t)和混凝土龄期(t′)的函数[20-21]：

Dt=Dr(tr/t)n

(1)

Dt=Dr(t′r/t′)n

(2)

式中：Dt表示随时间衰减的氯离子扩散系数，mm2/a；t表示混凝土暴露于氯离子环境中的时间，a；t′表示混凝土的龄期，a，且t′=t0+t；t0表示混凝土开始暴露于氯盐环境的龄期;Dr表示在参考暴露时间tr(或参考龄期t′r)时的混凝土氯离子扩散系数，mm2/a；n为氯离子扩散系数的衰减系数，是无量纲参数，可表征混凝土材料的氯离子扩散系数随时间衰减的快慢程度。

基于Fick第二定律，并考虑氯离子扩散系数的衰减性能时，氯离子二维扩散方程为[6]

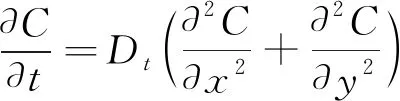
(3)

式(3)中：C表示混凝土中氯离子浓度，%，表示氯离子质量占混凝土质量的百分比)。

通过变量替换∂T/∂t=Dt，可得到常系数扩散方程：

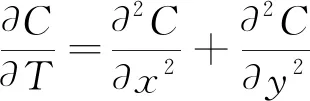
(4)

由于式(3)中t表示混凝土暴露于氯盐环境中的时间，根据混凝土的暴露时间域[0,t]，则中间变量T积分形式为

(5)

将式(1)、式(2)分别代入式(3)得

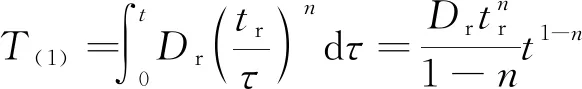
(6)

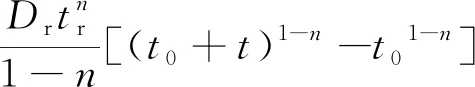
(7)

式中：t0表示混凝土开始暴露于氯盐环境的龄期，a；τ表示积分变量；n为氯离子扩散系数的衰减系数，是无量纲参数；T(1)、T(2)分别表示由式(1)、式(2)求得的中间变量，是无量纲参数。

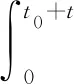
尽管如此，式(1)所表示的扩散系数时变模型存在较明显的缺陷，即当扩散时间t→0时，Dt→∞，与有限大小的混凝土实际氯离子扩散系数不符，因此采用式(2)进行计算。并且取t0=t′r=28 d=0.076 7 a。所以式(4)结合边界条件和初始条件C(x=0,y,t)=Cs，C(x,y=0,t)=Cs，C(x→∞,y→,t)=0，C(x,y,t=0)=0可得解析解：

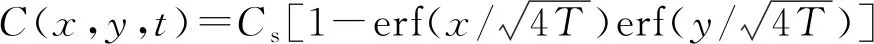
(8)

2 氯离子扩散系数时变衰减过程的随机性

衰减系数可以通过两种方式确定，一种是经验取值计算法，另一种是试验拟合方法。前者根据经验或规范建议的计算公式确定取值。试验拟合法是通过试验得到不同龄期混凝土的氯离子扩散系数，然后根据回归分析，拟合得到混凝土的衰减系数。然而，无论是经验取值法还是试验拟合方法所确定的氯离子扩散系数衰减系数值都无法准确地反映实际混凝土氯离子扩散系数的时变衰减性能，因此在分析混凝土结构中氯离子扩散规律时应该充分地考虑取值的随机性，通过可靠度方法计算混凝土结构的耐久性能。

欧洲技术指南DuraCrete中给出了不同种类的混凝土结构处于不同氯盐环境下时的扩散系数衰减系数的随机特性，其中概率分布类型统一为Beta分布。范宏[13]通过计算分析认为衰减系数的概率分布类型取正态分布更为合理。Saelensminde等[22]根据DuraCrete选取衰减系数的均值与标准差，概率分布类型采用正态分布。Nogueira等[23]和Peter等[24]分别取正态分布和对数正态分布进行计算。Gjørv[25]通过总结文献资料给出了海洋环境下潮汐区和浪溅区混凝土结构扩散系数衰减系数的取值，如表1所示，并采用正态分布类型对混凝土结构进行了服役寿命计算。

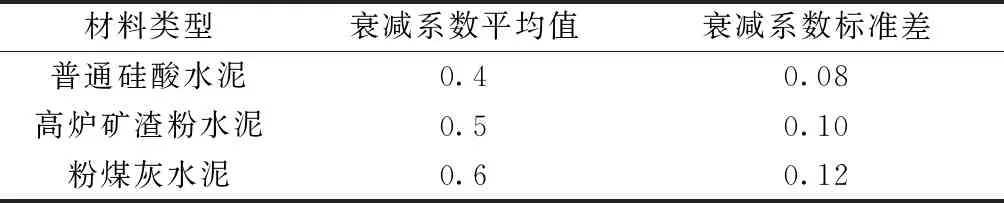
表1 衰减系数的部分建议值

3 时变扩散系数混凝土结构及参数敏感性分析

3.1 时变扩散系数混凝土结构可靠度

根据混凝土保护层厚度处(x=y=d)的氯离子浓度Cd=C(d,d,t)与钢筋脱钝阈值浓度(Cr)间的关系建立氯盐侵蚀下混凝土结构正常使用极限状态函数g=Cr-Cd。当采用式(8)计算Cd时，也可以根据服役时间建立正常使用极限状态函数[13]g=Tr-T，其中Tr=d2/[2erf-1(1-Cr/Cs)1/2]2。

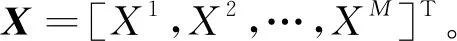
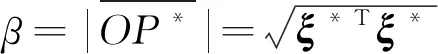
(9)

式(9)中：ξ*为验算点P*的坐标，可通过梯度优化迭代求解公式确定：

ξ(r+1)=[(ξ(r))Tα+b]{α}

(10)

式(10)中：ξ(r+1)、ξ(r)表示两相邻迭代步的验算点ξ*的坐标，其初始值可取{ξ}(0)=0；b和α分别表示迭代步长和迭代方向梯度，且

b=G(ξ(r))/‖G(ξ(r))‖

{α}=-G(ξ(r))/‖G(ξ(r))‖

(11)

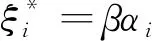
(12)

3.2 时变扩散系数混凝土结构可靠度参数敏感性分析

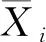
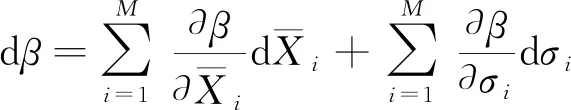
(13)

式(13)中：M表示随机变量个数。

式(13)可变为

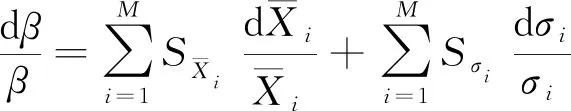
(14)

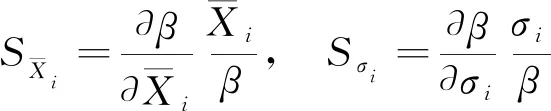
(15)

由式(9)和式(12)代入式(15)可得敏感系数：

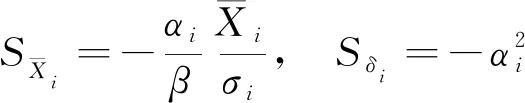
(16)

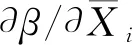
S1,i=-αi，S2,i=-β(αi)2

(17)

由于灵敏系数αi反映的是可靠指标对随机变量变异性的敏感性，式(17)从理论上证明了文献[14]定义的敏感系数S1,i和S2,i都只反映了可靠指标对随机变量变异性的敏感性，无法反映随机变量均值对结构可靠度的影响。分析可知，通过全微分定义的两个敏感系数能够分别反映随机变量本身及其变异性对结构可靠度的影响，克服了文献[17-19]所定义敏感系数的局限性。

4 算例分析

设一矩形粉煤灰混凝土桥墩位于海水浪溅区，截面尺寸为500 mm× 500 mm。根据《混凝土结构耐久性设计规范》(GB/T 50476—2008)，混凝土保护层厚度为60 mm，随机参数的具体统计特征信息如表2所示。

4.1 可靠度分析

采用本文方法分别计算：①不考虑氯离子扩散系数的龄期衰减特性；②考虑扩散系数的龄期衰减特性，但不考虑其衰减过程的随机性；③既考虑扩散系数的龄期衰减特性，也考虑其衰减过程的随机性三种情况下混凝土柱随着服役时间增加钢筋腐蚀概率的大小变化规律，分别用n=0、μn和μn+σn表示，计算结果如图1所示。图1中，MCS表示Monte Carlo 随机抽样方法，采用100 000次抽样进行计算。

从图1可以看出，本文方法与MCS方法相比，计算结果非常吻合，证明本文方法具有较好的计算精度。并且本文方法一般只需要不大于6次的迭代就能得到收敛的结果，比需要大量随机样本的MCS法效率要高得多。另外，从结构的可靠指标大小可以看出，与不考虑扩散系数的龄期衰减特性的情况相比，考虑衰减性能后可以显著提高混凝土结构的可靠度，而与忽略衰减系数随机性情况相比，考虑衰减系数的随机性时在结构服役前期则会明显降低可靠度。

分别取结构的目标可靠指标为1.3、1.5和1.8，采用T1、T2和T3分别表示n=0、μn和μn+σn这3种情况下的混凝土结构服役寿命，计算结果如表3所示。由表3可以看出，扩散系数的龄期衰减特性能显著地增加混凝土结构的服役寿命，忽视衰减系数的随机性就会过高估计了混凝土结构的服役寿命，从本算例的计算结果来看，当目标可靠指标分别为1.3、1.5和1.8时，由于忽视衰减系数的随机性而使混凝土结构服役寿命分别被高估了114%、115%和111%，说明忽视衰减系数的随机性会给服役寿命计算结果造成非常严重的误差。

取结构的可靠指标为1.5，按表1中的各参数的取值，保持衰减系数的变异系数取0.2不变，计算衰减系数均值取不同值时结构的服役寿命，计算结果如表4所示。从表4可以看出，随着混凝土扩散系数衰减系数均值的增大，是否考虑衰减系数的随机性对混凝土结构的服役寿命计算结果影响也越来越显著。因此，对于衰减系数较大的高性能粉煤灰混凝土结构来说，考虑衰减系数的随机性对准确地评估结构服役寿命就显得尤为重要。

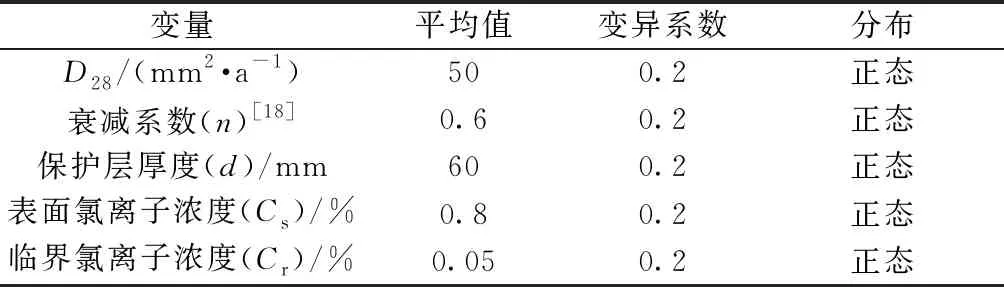
表2 随机参数的统计信息

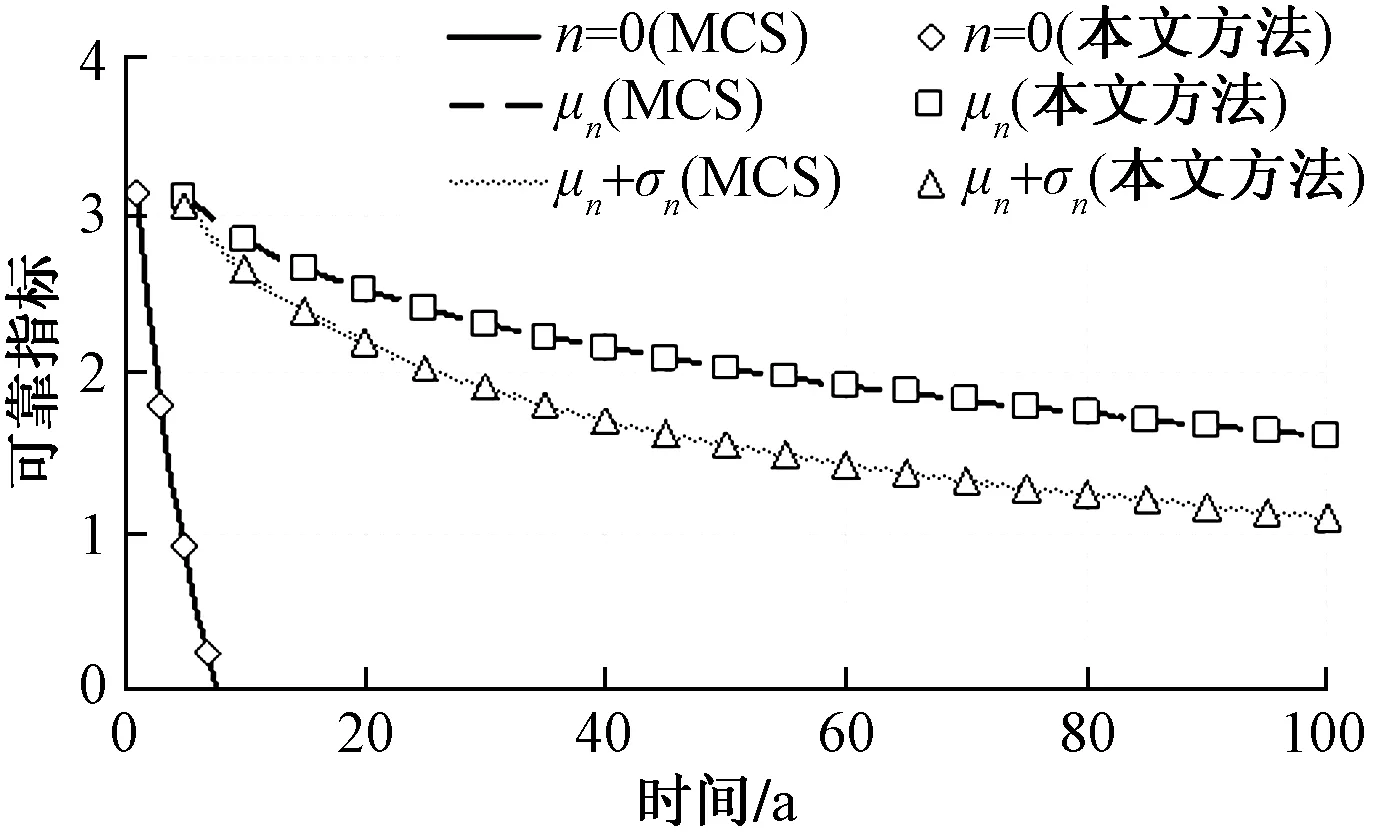
图1 混凝土桥墩的可靠指标Fig.1 Concrete bridge pier reliability indicators

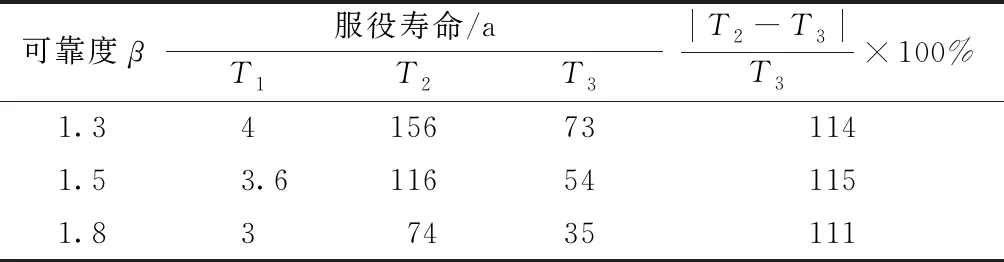
表3 目标可靠指标对服役寿命的影响

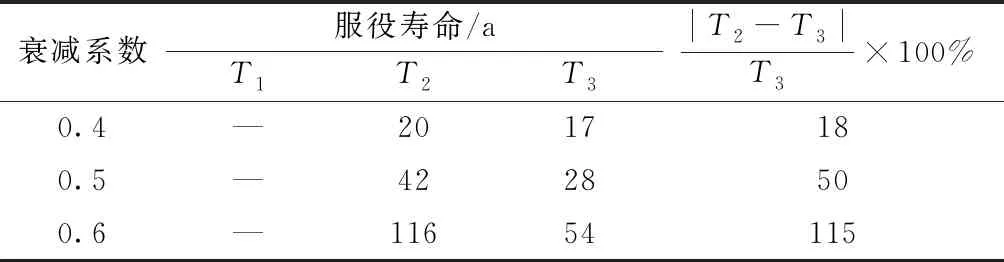
表4 衰减系数均值对服役寿命的影响

4.2 可靠度参数敏感性分析

为了进一步说明氯离子扩散系数衰减系数的随机性对混凝土结构可靠度的影响，根据推导的随机变量参数敏感系数计算了结构可靠指标对随机变量均值及变异性的敏感系数随机服役时间变化的规律，计算结果分别如图2、图3所示。从图2可以看出，随着结构服役时间的增加，各随机变量的均值对结构可靠度的影响都有增加的趋势，其中衰减系数的均值敏感系数增加速率最快，以致在服役时间大于40 a后，衰减系数的均值敏感系数不仅远远大于初始龄期氯离子扩散系数的均值敏感系数，还超过了保护层厚度的均值敏感系数，由此说明衰减系数对结构可靠度的影响与钢筋保护层厚度一样重要占主导地位。所以，正确地认识混凝土的抗氯离子扩散性能，考虑氯离子扩散系数的时变特性才能更准确地预测混凝土在氯盐侵蚀下的耐久性能。

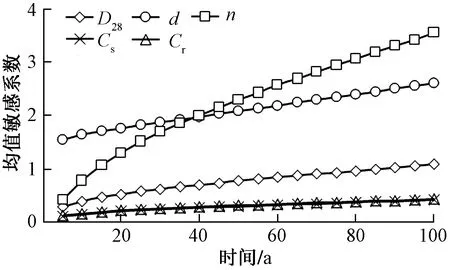
图2 均值敏感系数Fig.2 Mean sensitivity coefficient

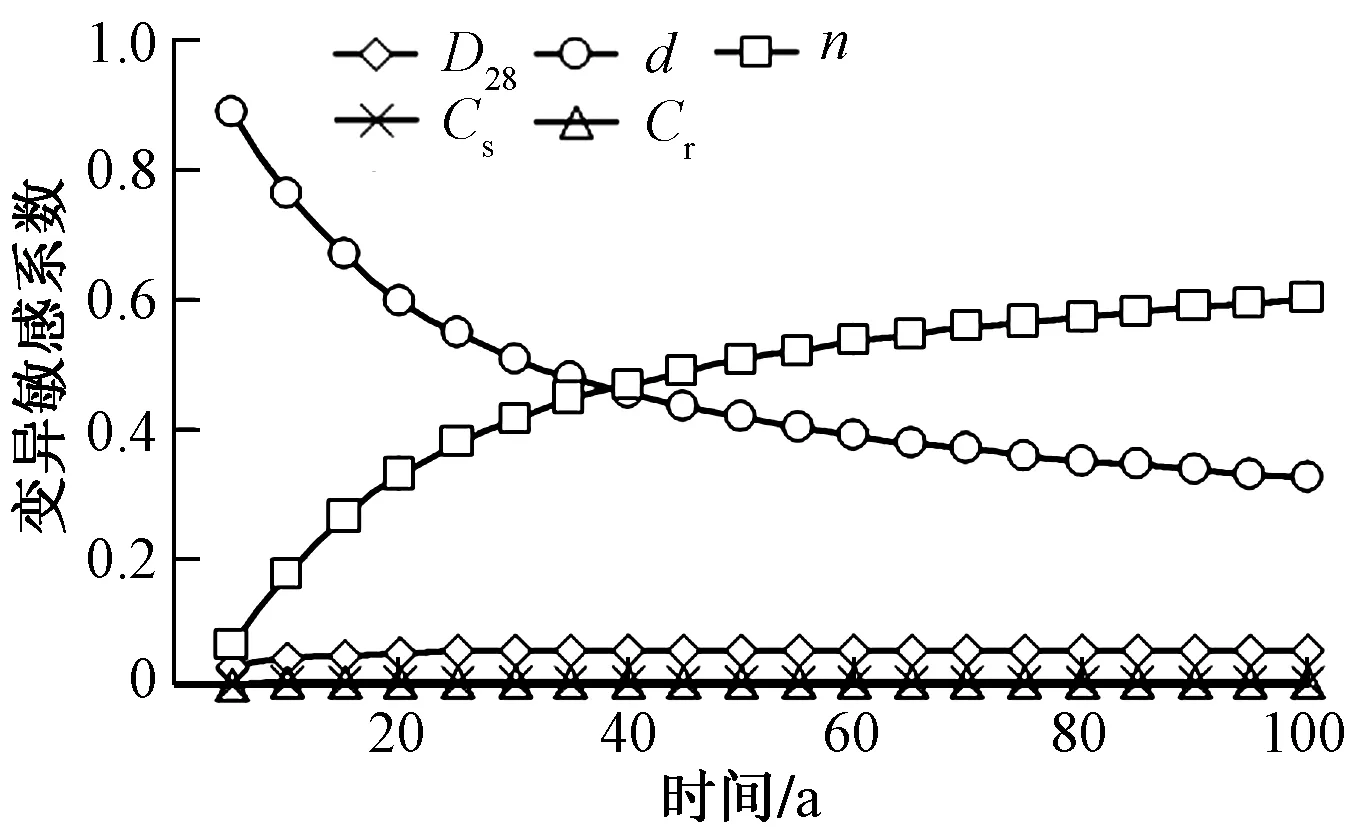
图3 变异性敏感系数Fig.3 Variability sensitivity coefficient

同样，从图3可以看出，衰减系数的变异性敏感系数绝对值随着服役时间的增加也逐渐增大，而保护层厚度的变异性敏感系数绝对值逐渐减小，导致在服役时间大于40 a后，衰减系数的变异性敏感系数超过了保护层厚度的均值敏感系数。图2、图3结果表明，混凝土氯离子扩散系数的时变性及其随机性对混凝土结构的耐久性能起着主导作用，忽略时变性会导致显著地低估结构的服役寿命，而若只考虑时变性不考虑时变衰减系数的随机性又会明显过高地估计结构的服役寿命。因此对实际的氯盐环境下混凝土结构进行耐久性设计和计算时，必须同时考虑混凝土氯离子扩散系数的时变性及其随机性。

5 结论

基于氯离子二维扩散模型考虑混凝土氯离子扩散衰减系数及其随机性，计算了氯盐侵蚀下混凝土结构的可靠度及服役寿命。为克服传统可靠度敏感系数的缺陷，分析氯离子扩散衰减系数及其随机性对混凝土结构耐久性的影响，根据全微分公式导出了可靠度对随机变量均值和变异性的无量纲敏感系数。计算结果表明，忽略氯离子扩散系数时变性会导致显著地低估结构服役寿命，而不考虑衰减系数的随机性又会明显地高估结构耐久性能。敏感性分析结果表明，混凝土氯离子扩散衰减系数与混凝土保护层厚度对氯盐侵蚀下混凝土结构耐久性的影响占主导地位，并随着服役时间的增加，衰减系数的影响会超过混凝土保护层厚度。