基于相关性分析方法建立混凝土RCM扩散系数多因素模型

周 明，董文秀，赵 宏，葛清蕴，常光明

（皖西学院建筑与土木工程学院，安徽六安237000）

暴露于氯盐侵蚀中的混凝土结构常由于氯离子的扩散而发生锈蚀[1]，导致过早被破坏，因此高耐久性、高性能混凝土设计与制备受到普遍关注。矿物掺和料具有良好的效应，可降低孔隙率，具有使混凝土更加密实、孔隙结构匀化等优点，大幅提高混凝土的氯离子渗透性。因此，近年来矿物掺和料普遍应用于抗Cl-耐久性混凝土的配合比设计和制备中[2,3]，但也导致混凝土的扩散系数与混凝土配合比参数关系更加复杂。混凝土的Cl-扩散系数是抗氯盐耐久性的重要指标，为定量分析混凝土的抗氯离子耐久性，有必要建立混凝土Cl-扩散系数与混凝土配合比参数的多因素模型。

在建模之前，应根据所需建立关系的特点选择建立模型的方法，该方法选择的合理性与否决定了所建立模型的优越性及合理性程度。传统建模方法无疑是正确并易于操作的，但仍然存在一些问题。在确定影响因素时，实际上很难确定所有的影响因素及各因素之间的耦合影响。如果考虑各因素之间的耦合影响特别是确定主导影响因素，将大大增加试验工作量和分析的难度；如果考虑过多的影响因素，将难以达到建立准确模型的目的。通过假设不同模型的统计分析建立模型，比较各模型之间的优越性后，最终确定优选模型。如果所假设的模型难以包含所有的耦合项，当所忽略的耦合项是一个权重较大的影响因素时，所建立的模型将难以准确描述客观规律，模型失真，即使通过增加大量试验也难以提高所建立模型的准确性，这也是现有科研的困境之一。

充分考虑氯离子扩散系数多因素模型的复杂性及代表性，运用收集数据、试验研究、数值模拟和数理统计分析，提出一种不依赖于假设模型的建模方法，即以确定各因素及因素之间高次耦合项的展开形式作为基础模型，通过数据与耦合项之间的相关性分析确定筛选耦合项，进而建立Cl-扩散系数与混凝土配合比参数的多因素模型，并以数理和实验数据分析验证所建立的模型及建模方法。

1 混凝土RCM扩散系数实验数据筛选及基本模型

1.1 实验数据筛选原则

混凝土扩散系数是混凝土中Cl-扩散速度的定量描述参数。扩散系数与混凝土本身的密实性、湿度状态及外界环境中Cl-的浓度、温度、电场等相关，即混凝土本身材料因素和外部环境因素共同决定了混凝土的Cl-扩散系数。而混凝土的Cl-扩散系数有多种实验测试方法，每种实验测试方法的结果存在一定差异。为了建立定量描述混凝土扩散系数的模型，选用国内外设计规范和指南所采用的RCM标准实验测试的数据作为研究对象，收集了各课题组[4-21]共计226组28 d龄期的混凝土扩散系数实验数据，在此基础上，建立标准实验条件下混凝土RCM扩散系数与混凝土材料参数之间的关系模型。

1.2 确定混凝土表观扩散系数多因素基本模型

水胶比是影响混凝土孔结构的重要因素，水胶比越小混凝土孔隙率越小，混凝土越密实，Cl-扩散系数越小。掺粉煤灰（FA）、矿渣粉（SG）或者复掺粉煤灰和矿渣粉的混凝土，由于粉煤灰、矿渣粉具有微集料、火山灰的形态效应，在一定掺量范围内使得混凝土具有更加密实、孔隙结构匀化等优点。因此，粉煤灰和矿渣粉的掺入会大幅改变混凝土耐久性能，使混凝土抗Cl-侵蚀能力得到增强。矿物掺和料加入后，由于水胶比、粉煤灰掺量、矿粉掺量等因素之间存在耦合影响，运用单因素的实验及研究方法难以建立准确的多因素模型。考虑混凝土各材料因素之间的相互耦合影响，混凝土中Cl-扩散系数用如下公式：

式中，f1,f2,f3,…,fn为混凝土RCM扩散系数D0的材料因素（水胶比W/B（f1）、粉煤灰掺量FA（f2）、矿粉掺量SG（f3）等独立参数。

式（1）RCM氯离子扩散系数D0可以用多元多项式展开式来表达，即：

式中，f1,f2,f3,…,fn为混凝土RCM扩散系数D0的材料因素。通过收集文献数据分析表明，可取一次和二次项作为混凝土RCM扩散系数的多因素模型D0的基本模型：

式（3）中展开式耦合项对预测模型的计算精度影响不同，运用皮尔逊相关系数ρ的计算公式进行相关性分析：

其中，X为因素项，Y为实验值，得到各一次、二次耦合项与RCM扩散系数试验值的相关系数如表1。

表1 耦合项与D0的相关系数ρ

一般相关性系数ρ在0-0.09之间为没有相关性，在0.1-0.2之间表示相关性较弱，在0.2-0.5之间为中等相关，在0.5-1.0之间为强相关。普通混凝土W/B越大，混凝土中可蒸发水越多，混凝土硬化后结构的孔隙率越大，氯离子渗透通道越多，扩散系数越大，因此Cl-扩散系数与水胶比体现高相关性；单掺粉煤灰混凝土，W/B仍然在一定程度上决定了可蒸发水数量，粉煤灰又能改善混凝土孔隙结构，因此粉煤灰掺量（f2）及掺量的二次项（f2×f2）都体现了一定的相关性；对于单掺矿渣混凝土，由于矿渣粉具有微集料效应，矿渣粉自身具有一定的水硬性，可在水化前期进行二次水化从而改善孔隙结构和数量，W/B、SG及耦合项、二次项都与Cl-扩散系数相关性较大；复掺粉煤灰和矿渣粉混凝土，由于多种材料之间的相互影响，耦合项的相关系数较大。

2 混凝土RCM氯离子扩散系数的多因素模型

依据1.2中相关系数的分析，提出耦合项中相关性不高的项，（3）式的展开式中不显著项剔除后得到：

式中，X1，X2，X3...见表1所示，k1，k11，k12…为拟合常数。基于收集文献中的试验数据[4-21]，通过最小二乘法进行伪线性拟合，得到混凝土RCM扩散系数的预测模型为：

图1为混凝土RCM扩散系数拟合模型即式（6）预测值与试验值的对比示意图。研究表明，混凝土扩散系数的变异系数达到0.3[22]，拟合模型保证率为90%时的上下限参考线的纵坐标值按照公式“横坐标值±1.645×变异系数×横坐标值”可以得到，即图1中预测模型下限和预测模型上限。当试验值与预测值相等时数据点将处于参考线（等值线）上，图1上的数据点与参考线越接近，表示试验值与模型预测结果越接近。从图1可见，绝大部分试验数据点（超过90%）分布于上下限参考线之间，表明预测模型能较好地体现RCM扩散系数和混凝土配合比参数之间的关系。

图1 混凝土RCM扩散系数模型预测值与试验值对比示意图

各类混凝土扩散系数模型与试验值之间的相关系数，以及模型拟合结果与总体数据之间的相关系数如表2。从表2可知，各类混凝土的RCM试验数据拟合的相关系数都大于0.72，总体数据的拟合相关系数达到0.85，可见基于相关系数建立混凝土RCM扩散系数拟合模型具有较高的效率和精度。

表2 混凝土RCM扩散系数拟合模型与试验值之间的相关系数ρ

3 模型的分析与验证

3.1 拟合模型分析

如果拟合得到的混凝土RCM扩散系数预测模型是混凝土扩散系数实际值的真实反应，对于任何一组配合比为的混凝土，则有混凝土的扩散系数实验值，即扩散系数实验值是以预测值为均值的正态分布。假设不同配合比的混凝土扩散系数的变异系数均相同为δ，则有DiμDi～N(1 ,δ2)。由于不同配合比混凝土之间是相互独立的，在进行实验时，每个不同测试数据之间也具备相互独立的特性，将试验值进行归一化处理即除以扩散系数模型值，处理后的数据应符合τ～N(1 ,δ2)。研究归一化处理之后，既可以通过分析实验数据与模型的误差是否符合正态分布，从而检验模型的合理性，也可以求得扩散系数的变异系数。

τ的累积概率函数为：

图2为扩散系数试验值归一化处理后数据的累计概率图。累计概率图与正态分布的累计概率图（图3）非常相似，表明归一化的扩散系数值的分布接近正态分布。

图2 扩散系数归一化处理后数据的累积概率图

图3 扩散系数归一化处理后数据的正态概率纸

根据正态分布函数式（7）求逆函数得到：

则z是τ的线性函数，分别以z和τ作为纵坐标和横坐标，绘制扩散系数归一化处理后数据点在正态概率纸上的分布图（图中空心圆点），并绘制正态分布参考直线（图中实直线）。结果如图3所示。实验数据在正态概率纸上成直线分布的区域较多，说明将扩散系数归一化处理实验数据点与参考直线比较吻合，只是在概率纸上的头和尾部分略有差异，描述为正态分布是合适的。

Lounis等[23]和Karimi等[24]研究认为扩散系数符合对数正态分布。对扩散系数试验值归一化处理后，通过数理分析验证是否符合对数正态分布LN( )λ,ζ（其中λ,ζ分别为统计参数），绘制扩散系数试验值归一化处理后数据的对数正态分布概率纸，如图4所示。扩散系数试验值归一化处理后数据与参考直线比较吻合，只是在头尾部分略有差异，将其分布描述为对数正态分布是合适的。

计算得到λ，ζ分别为-0.052 280 233，0.345 788 953。

图4 扩散系数试验值归一化处理后数据的对数正态分布概率纸

由图2、图3、图4可知，将RCM扩散系数试验值归一化处理后，其分布类型描述为正态分布或对数正态分布都是合适的，同时也表明所建立的模型具有较高的适用性和准确性。

3.2 拟合误差分析

拟合模型预测值与试验值的相对误差符合正态分布，表明拟合模型具有较高的预测效率。即对于RCM扩散系数试验值Di、模型预测值μDi（i=1,2,3,…,n），通过如下处理得到相对拟合误差：

模型拟合精度具有较高的拟合效果，相对拟合误差应符合正态分布。绘制相对拟合误差的累积概率图，如图5所示，RCM扩散系数试验值与模型预测值的相对误差的累计概率图与正态分布的累计概率图非常接近，表明RCM扩散系数相对误差的分布接近正态分布。

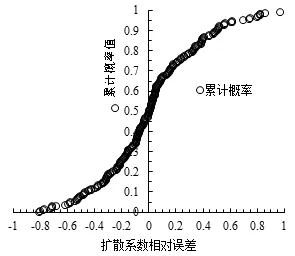
图5 扩散系数相对误差的累积概率图

图6 扩散系数相对误差的累积概率图

绘制相对误差在正态概率纸上的分布图，并绘制正态分布参考直线，如图6所示，相对误差在正态概率纸上成直线分布的区域较多，只有头、尾部和标准正态分布略有差别，表明将扩散系数归一化处理实验数据点与参考直线比较吻合，其分布描述为正态分布是合适的，所建立的拟合模型能比较准确预测混凝土RCM扩散系数。

3.3 试验数据验证

去除文献[25]中扩散系数大于18×10-8mm2/s、单掺粉煤灰掺量不超过40%、单掺矿渣粉掺量不超过60%、复掺粉煤灰和矿渣粉不超过60%及部分异常数据，最终得到58组数据。将这58组数据与预测模型进行对比分析，并绘制混凝土RCM扩散系数模型预测值与试验值的对比结果（图7）。取变异系数为0.3，因此，计算模型保证率为90%时上下限参考直线的纵坐标值按照公式“横坐标值±1.645×变异系数×横坐标值”可以得到，即图7中预测模型下限和预测模型上限。当试验值与预测值相等时数据点将处于参考直线上，图中数据点与参考直线越接近，表示模型预测结果与试验值越精确。由图7可知，绝大部分试验数据点（超过90%）分布于上下限参考直线之间，所建立的预测模型能较好地表征RCM扩散系数和混凝土配合比参数之间的关系。

图7 混凝土RCM扩散系数试验值在预测模型上下限范围内的分布示意图

4 结论

①考虑影响混凝土RCM扩散系数各因素之间的耦合影响，提出了一种考虑耦合项的建模方法，避免分析过程中忽略重要影响的耦合项。

②通过收集226组代表性的标准实验条件下的混凝土RCM试验数据，依据相关系数方法剔除不显著项，并利用最小二次伪线性拟合方法建立混凝土氯离子扩散系数的多因素（参数）预测模型。

③通过与试验数据的对比分析，验证了扩散系数预测模型的有效性和适用性，为混凝土RCM扩散系数预测与抗氯离子耐久性设计提供了基础和依据。