竖向开挖卸载应力引起的基坑坑底土体变形响应

章丽莎， 应宏伟， 张世民*， 魏 纲

(1.浙大城市学院工程学院， 杭州 310015； 2.浙江大学建筑工程学院滨海和城市岩土工程研究中心， 杭州 310058)

随着城市建设过程中地下空间的不断开发，涌现出了大量复杂的基坑工程。基坑开挖将引起坑底中的应力释放，一方面，坑底土体会发生回弹变形，并在坑底桩基础中产生拉应力，使桩身上浮甚至拉裂[1-2]；另一方面，坑底土体的强度和变形参数也会随着基坑开挖卸载而发生改变[3-5]，进而影响整个基坑工程的变形和稳定性。因此，在基坑开挖卸载效应相关研究中，坑底竖向卸载应力分布研究是一个重要的切入点。

《建筑地基基础设计规范》(GB 50007—2011)[6]采用Boussinesq解计算地基表面堆载或卸载引起的土体中的附加应力分布，由于该解答方便易得，被广泛地应用于基坑开挖引起的竖向卸载应力分布及其引起的回弹变形的计算[1, 7-8]。刘国彬等[3-4]根据大量的上海基坑工程实测资料，综合考虑基坑大小、开挖深度及围护结构形式等工程因素，提出了残余应力法用于计算基坑坑底的开挖回弹影响深度和回弹量。残余应力法是通过上海基坑工程经验总结得到的，学者们对该方法的应用或改进研究也多基于上海地区的工程实例开展[9-12]。对于基坑工程而言，开挖卸载对坑底土体的影响是发生在地基内部的，坑底开挖卸载应力的计算时更为准确的是采用Mindlin解答，但由于该解答较为复杂，在基坑工程回弹变形计算中的应用并不常见。

对不同基坑宽度、长度、开挖深度等条件下，对基于Boussinesq解和Mindlin解计算的竖向开挖卸载应力和回弹应力沿深度分布规律开展研究，提出了基于Mindlin解和自重应力抵消法的回弹影响深度和回弹变形计算的方法，通过3个工程实例与残余应力法及实测值进行对比分析。

1 竖向开挖卸载应力计算

1.1 规范法(Boussinesq解)

《建筑地基基础设计规范》(GB 50007—2011)[6]指出在地基变形计算时，地基内的应力分布可采用各向同性均质线弹性变形体理论进行求解，通过附加应力公式来表示堆载或卸载引起的地基基础中竖向应力(Δσz)沿深度的分布情况，如式(1)所示：

Δσz=αBp

(1)

式(1)中：p为地基表面堆载或卸载的总应力，对于基坑开挖的情况，卸载总应力为开挖深度范围内扣除浮力的土层自重应力；αB为基于半无限空间线弹性体表面作用力的Boussinesq解答得到的附加应力系数。规范法又称为附加应力法。

以基坑开挖面中心点以下的土体为研究对象，取开挖前基坑平面中心点为原点，建立坐标系，如图1所示。暂不考虑基坑开挖时竖向挡土结构变形引起的侧向应力的影响，采用规范法求解矩形基坑开挖在坑底土体中产生的竖向开挖卸载应力(ΔσzB)沿深度分布的解答为

ΔσzB=αBp=

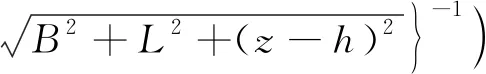
(2)

式(2)中：B为基坑宽度的1/2；L为基坑长度的1/2，且L≥B；h为基坑开挖深度；x、y、z为以基坑平面中心点为原点建立的笛卡儿坐标系，其中x、y表示基坑所在平面，z表示沿土层向下的深度。

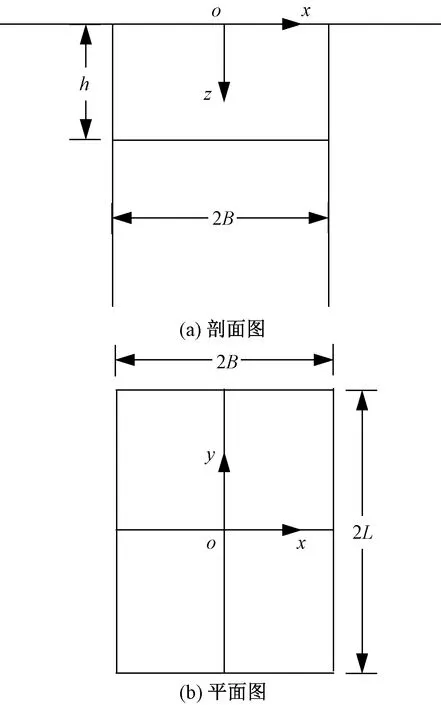
图1 基坑工程示意图Fig.1 The schematic diagram of the foundation pit

1.2 残余应力法

残余应力法认为开挖过程中基坑坑底土体中的应力未完全释放，会有部分应力残留。刘国彬等[3-4]基于大量的上海基坑工程经验，给出了考虑残余应力的竖向开挖卸载应力(Δσzc)表达式为

Δσzc=pc(1-αc)

(3)

式(3)中：pc为开挖深度范围内土层自重应力的总和；αc为残余应力系数，其表达式为

(4)

式(4)中：对上海地区软黏土而言，α0=0.3；由α=0.95定义的残余应力影响深度(hr)的经验表达式为

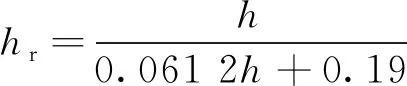
(5)

1.3 基于Mindlin解的竖向开挖卸载应力计算

事实上，基坑开挖是发生在地基内部的卸载，可采用徐志英[13]、周闻一[14]基于半无限土体内部作用集中力作用下土体内应力分布的Mindlin解[15]，推导的矩形面积均布荷载下土体中的竖向应力解析解，来表示开挖引起的基坑坑底中心点以下土体中的竖向卸载应力(ΔσzM)分布。

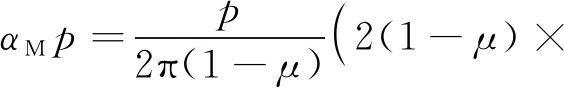
arctan{BL[(z-h)×

μ)arctan{BL[(z+h)×

h)[B2+L2+2(z-h)2]{[B2+

(z-h)2][L2+(z-h)2]×

(3-4μ)z][B2+L2+2(z+h)2]×

{[B2+(z+h)2][L2+(z+h)2]×

2BLhz(z+h)[3B2+2L2+

3(z+h)2]{[B2+(z+h)2]2[B2+

L2+(z+h)2]3/2}-1+2BLhz(z+

h)[2B2+3L2+3(z+h)2]

{[L2+(z+h)2]2[B2+L2+

(6)

式(6)中：μ为泊松比。

采用Boussinesq解和Mindlin解计算竖向开挖卸载应力两种方法本质上都是附加应力法，两者的区别在于附加应力系数的求解方法有所不同。

2 回弹应力的计算及其应用

2.1 回弹应力计算

自重应力抵消法[7-8]认为在基坑开挖引起的坑底回弹变形计算时，土的自重应力是土体回弹过程中的抗力，应予以扣除，但该方法计算卸载应力时采用的是Boussinesq解。

基于Mindlin解的竖向开挖卸载应力解答和自重应力抵消法，给出坑底回弹应力(Δσrz)的表达式为

(7)

式(7)中：γ′i为坑底以下第i层土的有效重度；hi为坑底以下第i层土的厚度。

需要注意的是，基坑开挖对坑底桩基础的影响是由坑底土体的回弹变形引起的，因此认为应采用回弹应力计算坑底桩基础的受力，而不是直接采用基于附加应力法求解的开挖卸载应力。

2.2 开挖回弹影响深度和回弹变形计算

当基坑的长度和宽度均较大时，基坑支护结构的侧向应力对于坑底中心位置处回弹应力的影响，可以忽略不计[16]。当回弹应力等于零，即Δσrz=0，对应的深度z0为开挖卸载影响的最大深度。由此可得开挖回弹影响深度的表达式为

hr=z0-h

(8)

坑底开挖回弹变形(δ)的计算公式为

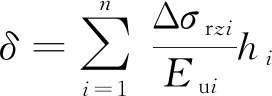
(9)

式(9)中：Eui为坑底以下第i层土的回弹模量。

基于Mindlin解的竖向开挖卸载应力解答和自重应力抵消法的开挖回弹影响深度和回弹变形的计算方法仅适用于不考虑支护结构侧向应力影响的大面积基坑中心区域的情况。

3 计算与分析

3.1 竖向开挖卸载应力的影响因素

3.1.1 长深比和宽深比的影响

令a=L/h，b=B/h，其中a为长深比，b为宽深比，由式(2)和式(6)可知，基于规范法和Mindlin解求得竖向开挖卸载应力解答可开展坑底竖向开挖卸载应力比(Δσz/p)随深度比(z/h)分布的无量纲分析。选取具有代表性的基坑长宽比L/B=1、2、 5、10、50及宽深比b=0.2、 0.4、 1、 2、 5，长深比可通过长宽比和宽深比确定(a=bL/B)；对于软土基坑而言，泊松比(μ)取值为0.3～0.5，图2的计算分析中，取μ=0.35；开展不同长深比(a)和宽深比(b)条件下，基坑开挖引起的坑底竖向开挖卸载应力比沿深度分布的研究。

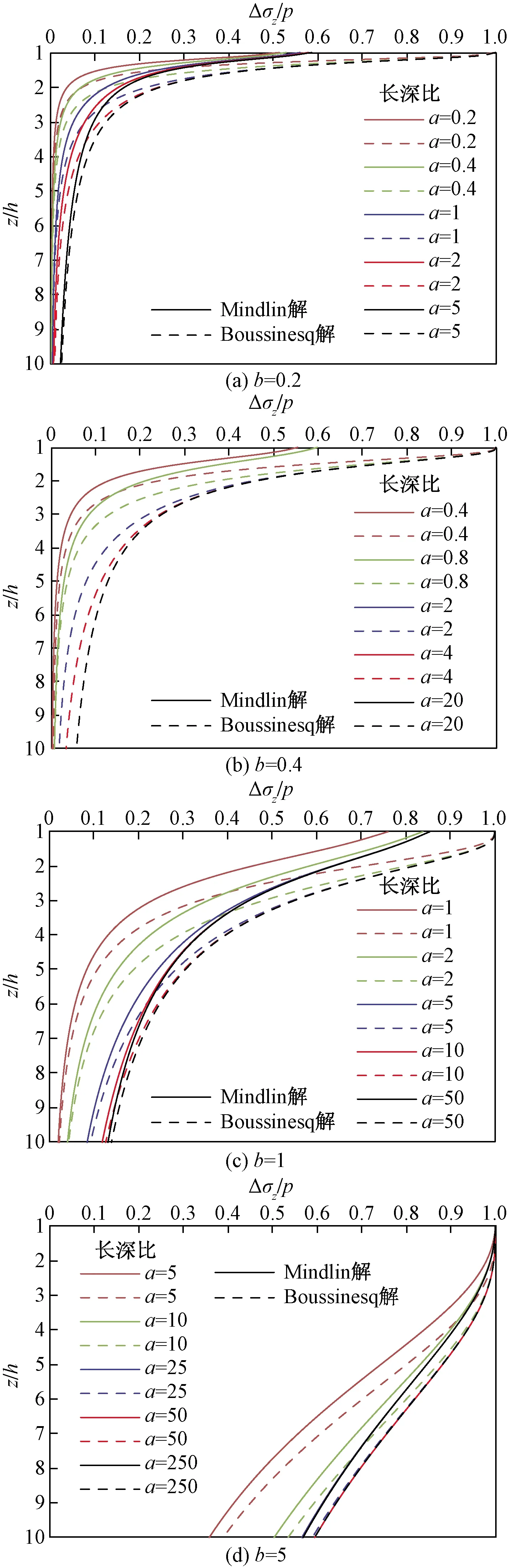
图2 宽深比和长深比对竖向开挖卸载应力比沿 深度分布的影响Fig.2 Influence ofwidth-excavation depth ratio and length- excavation depth ratio on the distribution of excavation- induced vertical unloading stress ratio against depth

从图2可以发现，基于Boussinesq解和Mindlin解的竖向开挖卸载应力比沿深度分布均受宽深比和长深比的影响：基于Boussinesq解的竖向开挖卸载应力比在坑底处始终为1；在坑底附近基于 Mindlin 解的竖向开挖卸载应力比是随基坑的宽深比和长深比不断变化的，当宽深比和长深比均较大(如a≥5,b≥5)时，基于Mindlin解的竖向开挖卸载应力比接近于1，与基于Boussinesq解的结果接近。

对于窄基坑(b≤0.4)[3]，竖向开挖卸载应力沿深度迅速衰减，在靠近基坑坑底基于Boussinesq解和Mindlin解的结果相差较大。随着宽深比的不断增大，基坑坑底附近基于Boussinesq解和Mindlin解的竖向开挖卸载应力比的差异不断减小。当宽深比达到5时，基坑坑底以下一倍开挖深度范围内基于Boussinesq解和基于Mindlin解的竖向开挖卸载应力比均接近于1。

当基坑的宽深比一定时，随着长深比(长宽比)的增大，基于Boussinesq解和Mindlin解的竖向开挖卸载应力比沿深度衰减均减弱，分布曲线均向右移。如图2所示，当长宽比(L/B)大于5时，基于Boussinesq解和Mindlin解的竖向开挖卸载应力比沿深度分布曲线在坑底一定范围内分别重合；随着深宽比的增大，该重合深度增大；如图2(d)所示，当宽深比达到5时，长宽比大于5的基于Boussinesq解和Mindlin解的竖向开挖卸载应力比沿深度分布曲线在整个计算深度范围内分别重合，但是两者解答仍存在差异，说明基于Boussinesq解和Mindlin解求得的竖向开挖卸载应力是有差别的。

3.1.2 泊松比的影响

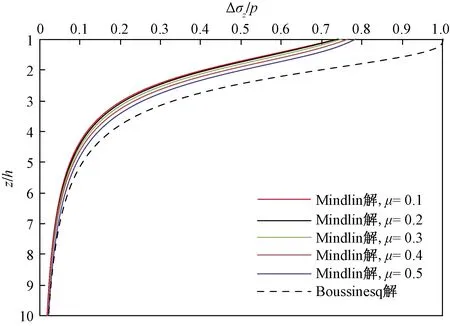
图3 泊松比对竖向开挖卸载应力比沿深度分布的影响Fig.3 Influence of Poisson ratio on the distribution of excavation- induced vertical unloading stress ratio against depth

选取具有代表性的泊松比(μ)为0.1、0.2、0.3、0.4、0.5，取a=b=1，讨论不同泊松比对竖向开挖卸载应力比沿深度分布的影响。如图3所示，泊松比越大，基于Mindlin解的竖向开挖卸载应力比沿深度分布曲线向右移，越接近于基于Boussinesq解的结果。

3.2 回弹应力的影响因素

3.2.1 不同长深比和宽深比的影响

假定基坑土层均匀，地下水位线位于地表处，不考虑开挖基坑内降水的影响，选取与图2相同的长深比和宽深比变化范围及泊松比，开展不同长深比和宽深比对基坑开挖引起的回弹应力比沿深度分布的研究。

由图4可知，当宽深比小于5，且长宽比大于5时，基于Boussinesq解的回弹应力比沿深度分布曲线几乎重合；基于Mindlin解的回弹应力比沿深度分布曲线则在宽基坑[如图4(c)]时才重合。当基坑宽深比等于5时，基于Mindlin解的回弹应力比解答与基于Boussinesq解的结果几乎重合。

不同长深比和宽深比对基坑开挖引起的回弹应力比沿深度分布的影响与其对竖向开挖卸载应力的影响大致相同。对于地下水位线位于地表处的均质土基坑而言，开挖回弹影响深度在一倍开挖深度以内；当考虑地下水位线低于地表以及基坑内降水等因素时，回弹影响深度将增大。基于Mindlin解的回弹应力比和回弹影响深度较基于Boussinesq解的结果要小，当基坑宽深比小于5时，两者的结果有显著的差别；当基坑宽深比等于5时，如图4(d)所示，两种方法计算的回弹影响深度的差别为0.01～0.02倍的开挖深度，当基坑开挖深度较大时，该差异不可忽略。由此可见，基坑开挖回弹应力和回弹影响深度的计算应采用基于Mindlin解的解答。

如图4(a)、图4(b)所示，对于窄基坑，基于Mindlin解的回弹应力比沿深度分布曲线呈弱非线性；随着基坑宽深比的增大，如图4(c)、图4(d)所示，基于Mindlin解的回弹应力比分布曲线呈明显的线性分布。在大型基坑工程的开挖回弹影响深度和回弹变形计算时，可采用基于Mindlin解的回弹应力的线性分布拟合公式。

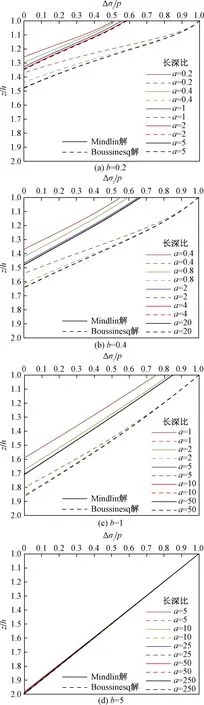
图4 宽深比和长深比对回弹应力比沿深度分布的影响Fig.4 Influence of width-excavation depth ratio and length-excavation depth ratio on the distribution of rebound stress ratio against depth

3.2.2 泊松比的影响

泊松比对回弹应力比沿深度分布的影响，与其对竖向开挖卸载应力的影响类似，即泊松比越大，基于Mindlin解的回弹应力比分布曲线向右移，越接近于基于Boussinesq解的结果。

3.3 工程应用

由上述研究分析可知，回弹影响深度和回变形的计算方法适合开挖长度和宽度均较大的基坑，因此，选取3个典型大面积基坑工程进行工程实例分析。

3.3.1 上海环球金融中心裙房基坑工程

上海环球金融中心裙房基坑工程[17]，长约 216 m，宽约125 m，开挖深度约18 m，采用逆作法施工，工程规模宏大，基坑保护等级为一级，该场地土层参数如表1所示。

取地下水位线位于地面以下0.5 m，不考虑坑内降水的影响(即卸载总应力计算时，地下水位线以下的土的重度取为浮重度)，下同。

首先计算总卸载应力为144.60 kPa，根据式(7)计算基坑开挖引起的坑底回弹影响深度为15.65 m，再由基于Mindlin解和自重应力抵消法提出的回弹变形计算式(8)求得坑底中心点的回弹变形量为4.622 cm，计算结果如表2所示。由表2可知，本文方法与自重应力抵消法的计算结果较为接近，与实测结果的误差最小。

3.3.2 上海虹桥枢纽西交通广场基坑工程

上海虹桥枢纽西交通广场基坑工程[9]，长约699 m，宽约199 m，以开挖深度为10 m处的区域为例，场地土层参数如表3所示，其中，④淤泥质黏土和⑤1-1黏土的回弹模量是根据土层编号及其埋深参考文献[8]确定的。

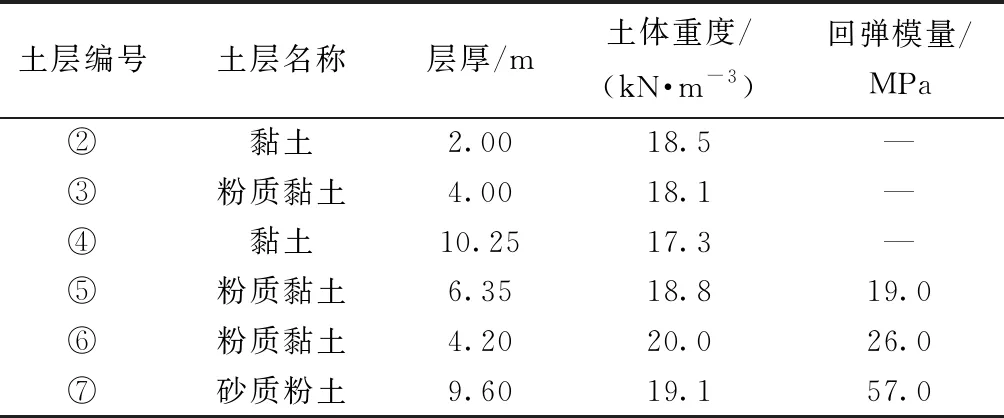
表1 上海环球金融中心裙房基坑工程土层参数[8]

表2 上海环球金融中心裙房基坑工程回弹变形计算结果

首先计算总卸载应力为80.15 kPa，通过式(7)计算坑底的回弹影响深度为10.55 m，再由式(8)计算坑底中心点的回弹量为6.743 cm，计算结果如表4所示。由于无实测数据，与残余应力法对比，两者回弹变形的计算结果相近。

3.3.3 上海某高层建筑基坑工程

上海某高层建筑基坑工程[3]，位于上海市东北区，基坑宽约38.7 m，长约61.45 m，深度约7.6 m，场地土层参数如表5所示。

该算例未直接给出回弹模量，根据回弹模量和回弹指数的关系[8, 18]，计算得到灰色砂质粉土和灰色淤泥质泥黏土的回弹模量分别为10.16、11.76 MPa。通过计算得到总卸载应力为72.07 kPa，由式(7)计算坑底的回弹影响深度为8.60 m，再由式(8)计算坑底中心点的回弹量为2.77 cm，计算结果如表6所示。结果表明本文方法的回弹量计算结果与实测回弹量相符，较其他方法的计算结果更可靠。

通过基坑工程实例中回弹变形的计算结果对比，充分说明本文方法适用于大面积基坑中心区域的回弹变形计算，结果精度高。

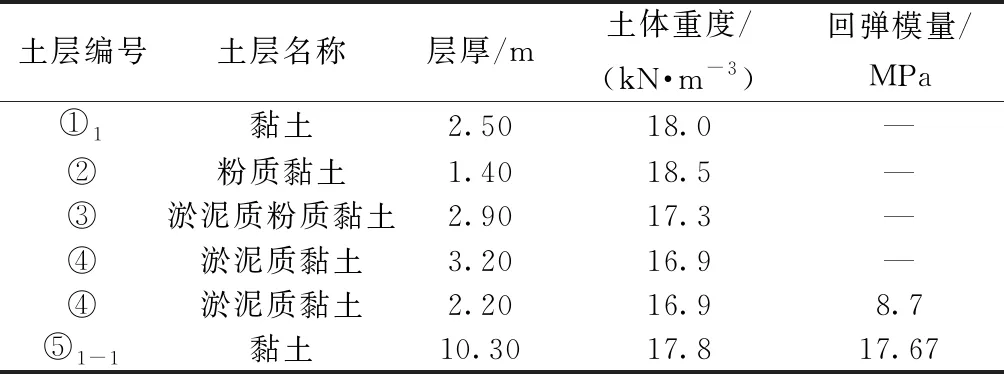
表3 上海虹桥枢纽西交通广场基坑工程土层参数[8-9]

表4 上海虹桥枢纽西交通广场基坑工程回弹变形计算结果

表5 上海某高层建筑基坑工程土层参数[3，11]

表6 上海某高层建筑基坑工程回弹变形计算结果

4 结论

(1)基于Mindlin解和Boussinesq解的基坑坑底竖向开挖卸载应力比沿深度分布曲线有着明显差异，随着宽深比和长深比的增大，该差异将减小，但不可忽略。

(2)基于Mindlin解的竖向开挖卸载应力、回弹应力和回弹影响深度与基坑开挖的长深比、宽深比和泊松比正相关；当基坑的宽深比和长深比均较大(如a≥5,b≥5)时，坑底附近基于Mindlin解的竖向开挖卸载应力比约为1。

(3)当基坑宽深比小于5时，基于Mindlin解的回弹应力比和回弹影响深度明显地比基于Boussinesq解的结果要小；当基坑宽深比等于5时，基于Mindlin解的回弹应力比解答和基于Boussinesq解的结果几乎重合，但两种方法计算的回弹影响深度差值为0.01～0.02倍的开挖深度，当基坑开挖深度较大时，该差异不可忽略；对于基坑工程而言，应采用基于Mindlin解的坑底开挖回弹应力和回弹影响深度计算方法。

(4)基于Mindlin解的竖向开挖卸载应力解答和自重应力抵消法的开挖回弹影响深度和回弹变形的计算方法仅适用于不考虑支护结构侧向应力影响的大面积基坑中心区域的情况；可采用基于Mindlin解的回弹应力的线性分布拟合公式直接计算。

(5)通过上海地区的3个大规模基坑工程实例计算比较，本文方法的计算值接近实测值，且精度高于其他已有计算方法，说明本文方法可直接用于大面积基坑工程开挖回弹影响深度和回弹变形的计算。