W波段目标模拟带外噪声抑制技术
2020-12-26王立权陈德红
王立权,漆 斌,黄 杉,肖 梁,陈德红
(1. 上海机电工程研究所,上海 201109;2. 东南大学 毫米波国家重点实验室,江苏 南京 210096)
0 引 言
随着雷达及无线通信技术的迅猛发展,无线电频谱的应用也随之拓展,目前W波段的雷达探测技术、目标模拟技术研究已成为被关注的热点[1-2]。由于W波段工作频率较高,目标模拟系统链路通常需要通过上变频将微波信号变频到W波段,但是变频链路引入的本振泄露、镜像、交调等信号会直接影响目标模拟系统的动态范围甚至可能产生假目标[3],因此需要设计W波段滤波器来抑制带外杂波、噪声信号。
一般采用带通滤波器来实现对W波段带外杂波信号的抑制,常规微带带通滤波器存在插入损耗较大(≥4 dB)、带外抑制低(≤25 dB)的问题[4]。因此,近年来通过带阻滤波器实现带外杂波抑制的技术正在渐渐兴起。2004年,KNYAZKOV基于彼此相对旋转的两个偏振反射器来创建波导型偏振滤波器,并通过计算测量发现,这种偏振波导带阻滤波器较适用于毫米波和亚毫米波准光接收系统[5],体积结构比较大。2015年,HICKLE等利用E模谐振器实现了带宽可调、高隔离度的带阻滤波器,工作在75~108 GHz,实现了极窄的阻带(1.5%、3 dB带宽)及抑制大于70 dB的陷波[6],该滤波器适合用于对点频干扰或杂散的抑制,却不适合有一定阻带带宽要求的应用。同年,JIN等采用折叠裂环设计了一款E平面波导滤波器,通过在波导E面膜片上加载折叠裂环实现了在W频段的多阻带带阻滤波器[7],同样这种滤波器是基于波导结构的滤波器,其体积不小于19 mm×19 mm×30 mm。2016年,李建东通过引入不同尺寸的开口谐振环和加载变容二极管的谐振环,成功设计出一款基于人工表面等离激元且工作于毫米波段的带阻滤波器[8],验证了人工表面等离激元设计滤波器的可行性,这种结构虽然采用了类似平面电路的结构,但是其尺寸比较大,也不利于与其他平面电路的集成。
综合上述,W波段微带带通滤波器的插入损耗较大、带外抑制低,而波导及腔体滤波器的尺寸、重量较大,不利于整个目标模拟系统的集成。因此本文提出一种通过低通原型滤波器结合四分之一波长微带短截线的微带带阻滤波器设计方法,解决滤波器插入损耗大、带外抑制低、体积大的问题,用于实现W波段目标模拟系统的低噪声前端设计和集成。
1 W波段目标模拟链路
W波段目标模拟系统链路通常需要通过上变频将微波信号变频到W波段,系统原理框图如图1所示。假设本振信号为cos(ω0t),微波目标模拟信号为cos(ωIFt),那么理想的变频效果是:得到上边带信号cos[(ω0+ωIF)t],或者下边带信号cos[(ω0-ωIF)t]。
但是实际变频过程中,上边带、下边带、本振泄漏信号会相互交调生成一系列的频谱组合信号,同时变频将产生许多寄生的高次分量,这些寄生响应会产生寄生的互调中频分量,如果寄生响应大,就会对本振和输出信号产生影响[9]。图2给出了微波宽带信号跟W波段本振信号混频后产生的输出信号频谱图。从图2可以看出,输出信号除了包含所需的信号外,还包含了大量的交调、寄生信号。

图2 W波段上变频信号频谱图Fig.2 Specrtrum after up-conversion at W-band
因此,W波段目标模拟系统的设计中,需要通过采用如图1所示的带外杂波抑制技术来抑制变频链路引入的本振泄露、镜像、寄生分量等信号,输出如图3所示的理想的变频信号。

图3 W波段上变频信号滤波后的频谱图Fig.3 Specrtrum after up-conversion and noise filtering at W-band
2 带外杂波抑制原理
对本振泄漏、混频镜像等带外杂波的抑制一般通过滤波器实现,集总元件低通滤波器原型是设计各种低通、高通、带通、带阻滤波器的基础。图4所示的是一个典型的低通原型滤波器:ZA表示输入阻抗;ZB表示负载阻抗;g1、g3、g5表示集总元件的电感;g2、g4、g6表示集总元件的电容[8,10]。

图4 低通原型滤波器结构图Fig.4 Structure of lowpass prototype filter
图4所示的低通原型滤波器采用的是集总元件,因此滤波器不具备周期性。如果将低通原型滤波器的集总元件转化为微带短截线,利用微带线的周期性,就可以变换为带阻滤波器。
假设图4所示的低通滤波器中g1、g3、g5的电感为L,那么对应的阻抗为
ZL=jΩL
(1)
式中,Ω为电感的角频率变量。
四分之一波长短路微带短截线的输入阻抗可表示为[7]
(2)
式中:ω是工作角频率;ω0是微带的特征角频率;Z0是微带的特征阻抗。
采用微带短截线替代集总电感,那么就要使集总电感和短截线等价,则有
(3)
式(3)可以转化为
(4)
式中,k=L/Z0,可以通过调整微带线的特性阻抗调节参数的取值。
同理可证集总电容到分布开路短截线的频率变换式,根据式(3)~(4)可知,微带短截线滤波器具备以2ω0为周期的周期性,因此可以将集总低通滤波器变换为带阻滤波器。图4中的电感和电容变换为微带短截线滤波器后,其框图如图5所示。图中:Z1、Z2、Z3是电感的等效短截线;Y1、Y2、Y3是电容的等效短截线;Z0A、Z0B是单位元件,即一段特性阻抗等于终端阻抗的无耗传输线,Z0A的特性阻抗匹配输入阻抗ZA,Z0B的特性阻抗匹配源阻抗ZB,单位元件的增加并不会影响系统的频响性能。

图5 采用微带短截线的带阻滤波器Fig.5 Band-stop filterincluding microstrip
实际应用过程中,难以实现图5中的串联微带短路短截线,因此需要通过黑田规则(Kuroda’s identities)将微带短路短截线变换为开路枝节,短截线变换的等效关系如图6所示,具体的转化如式(5)所示[8,11]。
(5)
式中,Z0、Z′0、Zs、Ys分别是单位元件的特性阻抗或导纳。

图6 黑田规则变换示意图Fig.6 Equivalent circuits for Kuroda identities
通过多次黑田变换,图5所示的带阻滤波器可转化成如图7所示的基于开路枝节短截线及单位元件的分布参数的带阻滤波器结构[7]。其中:ZA、ZB为输入端和输出端的终端阻抗;Zn是四分之一波长的微带传输线的特性阻抗;Yn为并联开路短截线的特性阻抗。
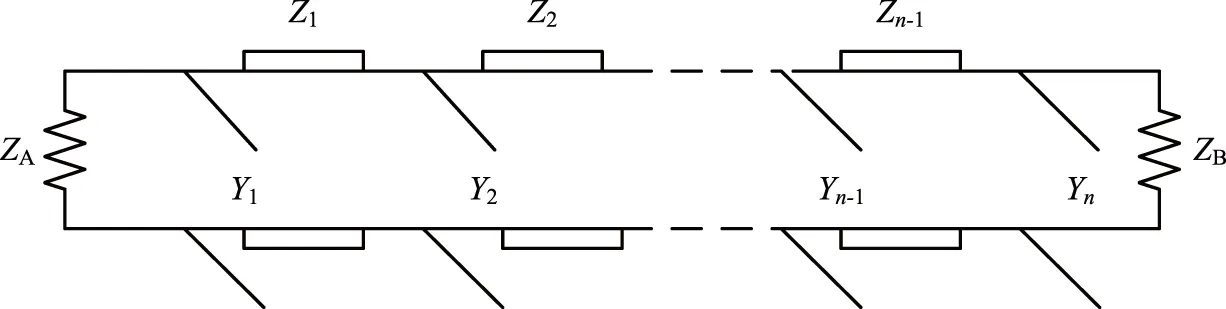
图7 微带带阻滤波器结构Fig.7 Band-stop microstrip filtertopology
图7给出了采用微带短截线将集总低通滤波器变换为带阻滤波器的原理框图。滤波器频率响应如图8所示,其中:(a)图表示采用集总元件的低通滤波器频率响应;(b)图表示采用微带短截线的带阻滤波器响应。

图8 滤波器频率响应Fig.8 Frequency response of filters
3 仿真与测试
为了验证上述基本原理及分析的有效性,对W波段微带带阻滤波器进行设计和仿真。假设微带带阻滤波器的阻带为84~89 GHz,抑制效果不小于30 dB,通带为96~104 GHz,带内插入损耗不大于2 dB。滤波器阶数的增加有利于带外杂波的抑制,但是会影响带内的插入损耗,因此兼顾考虑这两个因素,本文采用五阶带阻滤波器。低通滤波器的原型参数可查表得到[8,12],然后根据实际的工作频率结合微带特性转化为带阻滤波器结构,如图9所示。滤波器的输入和输出负载的阻抗特性一般都是标准的50 Ω接口,因此滤波器是一个左右对称的结构。图9中:W0是连接线的宽度;Wab、Wbc的是低阻串联微带线的宽度;Wa、Wb、Wc的是高阻并联微带线的宽度;L0是连接线的长度;Lab、Lbc的是低阻串联微带线的长度;La、La2、Lb、Lb2、Lc、Lc2的是高阻并联微带线的长。并联微带线与串联微带线的连接存在一个T型接口,如图10所示,因此需在仿真软件中建立的串并联连接模型,并使用deembed对端口的尺寸进行微调、校准。

图9 微带带阻滤波器布局图Fig.9 Layout of microstrip band-stop filter

图10 微带串并联连接布局图Fig.10 Layout of microstrip and open-circuited stub
滤波器使用石英基片,相对介电常数为3.78,基片厚度为0.1 mm,微带线导体厚度为2 μm,根据以上条件以及如图9所示的滤波器结构,带阻滤波器的各部分尺寸如表1所示,对应的S参数仿真结果如图11所示。由图11可以看出,工作频率在84 GHz和89 GHz时,带阻滤波器的抑制度均优于-37 dB;滤波器在84 GHz和89 GHz处存在带外传输零点,其中在89 GHz处的带外抑制度更是高达50 dB。这说明该带阻滤波器具有非常陡峭的过渡带。由图11还可以看出,该带阻滤波器在96~104 GHz处有良好的通带特性,插入损耗小于2 dB。

表1 微带带阻滤波器布局参数表Tab.1 Parameters of microstrip band-stop filter layout

图11 带阻滤波器S参数仿真结果Fig.11 Simulated S-parameters of band-stop filter
所设计的微带带阻滤波器实物如图12所示,其中,(a)图为滤波器在W波段目标模拟系统中应用的链路,(b)图为滤波器的剖面示意。滤波器通过E面微带探针实现微带准横电磁波(transverse electromagnetic wave, TEM)模式与波导横电波(transverse electric wave,TE10)模式的有效转换。微带带阻滤波器的测试结果如图13所示,从测试结果可以看出,宽带带阻滤波器的阻带抑制大于36 dB,2个带外传输零点分别位于84.25 GHz和89.5 GHz处,滤波器的回波损耗小于-14 dB,带内(96~104 GHz)插入损耗小于2 dB(减去夹具损耗2 dB),性能优于同频段的微带带通滤波器。采用此带阻滤波器可以有效地抑制本振泄漏、混频镜像等杂散信号,提高系统的性能。另外,为了评估石英基片表面导体镀层厚度对性能的影响,进行了不同镀层厚度下的滤波器性能仿真,图13给出了不同镀层厚度t下S参数实测与仿真数据的对比,可以看出,微带线导体厚度对滤波器的性能影响较小。

(a) 含带阻滤波器的W波段目标模拟链路

(b) 带阻滤波器剖面图

图13 带阻滤波器S参数实测与仿真数据Fig.13 Measured and simulated S-parameters of band-stop filter
4 结束语
本文通过对W波段目标模拟系统由变频链路所引起的带外杂波信号进行分析,提出一种从低通原型滤波器结合四分之一波长微带短截线的W波段微带带阻滤波器设计方法,并且分析了四分之一波长串并联微带线的开路高阻线等效变化。利用ADS仿真软件,对滤波器的原理电路进行了验证,成功设计了一款尺寸1.3 mm×8.5 mm×0.1 mm的基于石英基片工艺的五阶带阻滤波器,相对于基于波导机构的滤波器,尺寸大幅缩减。该滤波器通带覆盖96~104 GHz,通带的带内插入损耗小于2 dB,带外杂波抑制大于30 dB,分别优于常规微带带通滤波器2 dB和5 dB。测试结果表明,所设计的带阻滤波器具有较好的通带损耗和带外抑制性能,可用于抑制W波段目标模拟系统的带外杂波信号。
