地海杂波统计特性研究概述

陈 岩，李艳艳，杨立波，倪兴虎，杨柏胜，王亚辉

(1. 北京航天自动控制研究所，北京 100854； 2. 宇航智能控制技术国家级重点实验室，北京 100854)

0 引 言

精确制导技术中，雷达是最重要的探测设备之一，它对目标的检测、识别与跟踪关乎精确制导的精度和性能。然而对于地面目标，由于目标周围场景存在较强的回波，目标与背景的对比度不高，导致雷达对目标的检测、识别性能严重降低，给精确制导武器的探测制导系统带来了巨大的挑战。

与探测设备本身带来的噪声不同，杂波是指雷达接收信号中由地面地物、海面、云雨雾等引起的回波分量。噪声可以通过电子设备的优化设计进行改善，而由目标周围区域场景引起的杂波只能从信号处理的角度对其进行区分，加以抑制或者滤除。因此，研究杂波特性并以此指导雷达信号处理算法设计，优化雷达检测性能，是一项极其重要的工作。

从信号处理的角度，人们主要关心的是如何对杂波回波进行建模[1]。本质上，杂波是大量散射体回波叠加的结果，如果散射体稳定，其回波也是稳定的；但是由于杂波内部的相对运动，比如海面运动、草木随风飘动等，都会使得各散射体回波相位发生变化，而回波对于相位变化是极其敏感的，这最终导致了回波的起伏，即杂波。因此，杂波具有类似热噪声的特性，单个分辨单元的回波具有随机的幅度和相位，但是杂波与热噪声也有较大的区别。单个分辨单元的回波在时间上具有相关性，因而其功率谱不是白的。从这一点看，利用统计学手段研究杂波是合理的，杂波的统计模型主要包括杂波起伏特性概率密度分布模型、杂波相关特性功率谱模型和平均单位后向散射系数模型[2]。

当前，对地杂波统计建模的研究热度有所降低。首先，利用统计学手段研究杂波这种纯数学的研究方法，所得到的杂波模型不包含任何电磁散射机理和雷达探测机理，其数学过程相对简单。其次，杂波统计建模需要对大量的测量数据进行统计和拟合，目前能够使用的地海杂波公开测量数据仍局限于几个经典的数据库以及乌拉比等[3-6]开展的杂波测量实验，数据已经被挖掘到了极限，而开展新的地海杂波测量的成本极高，技术难度也较大。第三，受限于实验条件，杂波测量无法覆盖全频段、全使用条件，因此杂波统计模型需具备一定的频率外推和使用条件外推能力，但是当前所建立的杂波统计模型在外推方面实际应用效果欠佳。第四，杂波统计模型较多，适用范围和应用条件各不同，不同模型之间结果也不一致，这使得设计人员在应用这些模型时抱有很大的怀疑态度。最后，随着当前雷达技术的不断发展，频段、分辨率等不断提高，尤其是弹载雷达高空高速的使用条件导致很多雷达信号处理技术发生变化，使得之前的杂波统计模型适用性大大降低，雷达统计建模渐渐失去了应用价值。

即便如此，杂波统计建模仍然具有非常重要的工程意义，这主要是由地杂波的复杂性所决定的。简单来说，雷达地杂波特性主要受雷达参数、地面环境参数的影响。雷达参数是比较明确的，但是对于地面环境的描述则远远达不到“明确”和“定量”，只能定性地描述，如山地、丘陵、沙漠、草地、湖面等，再细致也仅能实现粗糙度、微起伏等微观结构的描述，以及平均介电常数、平均电导率等半定量描述。因此，即便对于电磁散射机理和雷达探测机理的建模完全准确，由于地面环境的复杂性带来的输入误差也会产生极大的偏差。

因此，为了弥补杂波统计建模研究与新型雷达探测以及弹载雷达应用之间的差距，亟需开展更多的工作。主要包括：①持续开展杂波测量工作，覆盖更宽的频带、更高的分辨率、更多的工作模式，以及更加严酷的工作条件；②针对弹载应用的特点开展新的杂波统计建模方法研究，建立适用于弹载高频高分辨多功能雷达的杂波统计模型；③在杂波统计模型中引入电磁散射机理和雷达探测机理，提高杂波统计模型的外推能力；④完善并简化杂波统计模型的适用条件，建立定量的模型置信度评价体系和方法，便于设计人员对其所使用的杂波统计模型进行完整系统的评价。

1 杂波统计建模常用的描述手段

雷达波束照射范围内的地海面是由大量的散射体构成的，由于地面地形、植被的多样性和海面波浪的多变性，雷达波束照射区域内的散射体会发生随机的运动和变化，从而引起回波在时间和空间上的起伏。因此，地海杂波是一种随机信号，对地海杂波特性的描述通常采用统计方法。

首先，对于地海杂波散射强度，通常用地海面散射系数的均值来表示。由于面目标的扩展性，习惯的做法是将散射系数归一化到单位面积上，又称为单位后向散射系数，用σ0来表示，无量纲。

其次，对地海杂波起伏特性，可用幅度统计分布表示。幅度分布给出了杂波幅值的相对分布关系，即杂波振幅的概率密度函数或分布函数。

第三，对地海杂波的自相关性，可用频谱表示。频谱又分为时间频谱和空间频谱，时间频谱表征了杂波以时间为自变量的序列的自相关性，空间频谱表征了杂波以位置为自变量的序列的自相关性。

地海面环境特性的多样性决定了地海杂波是多参变量，地海杂波统计特性的主要研究内容包括杂波的单位后向散射系数、幅度分布、时间相关性、空间相关性的函数表达式及其参数与雷达参数、地海面环境参数之间的定量和非定量关系，以及根据杂波特性反过来模拟生成杂波，这些过程也被称为杂波统计特性建模。

2 单位后向散射系数(均值特性)

单位后向散射系数又被称为归一化雷达散射截面(normalized radar cross section, NRCS)，定义为单位照射面积的雷达散射截面[7]，即

式中：S为被雷达照射的地面面积；σ为相应地面的雷达散射截面(RCS)；而σ0即相应地面的NRCS，无量纲。

研究表明，σ0与擦地角、频率、极化方式、地形地貌、覆被、含水量、海情海况、海冰、温度、含盐度等都有关系，通常我们将与场景相关的变量统归为一个名词描述，即场景类型，从而给出σ0与擦地角、频率、极化方式和环境类型的关系为

σ0=σ(φ,f,p,l)

式中：φ为擦地角；f为频率；p为极化方式；l为环境类型。

针对小范围局部均匀的地面或者某种海况的海面建立的上述函数关系，并确定相应参数，便被称为散射系数模型。

2.1 散射系数的一般规律

在不同擦地角下，对于同一地海面起决定作用的散射机制是不同的。一般而言，散射系数随擦地角的变化可分为3个独立的区间，即准镜面反射区、平坦区和近掠射区，如图1所示。

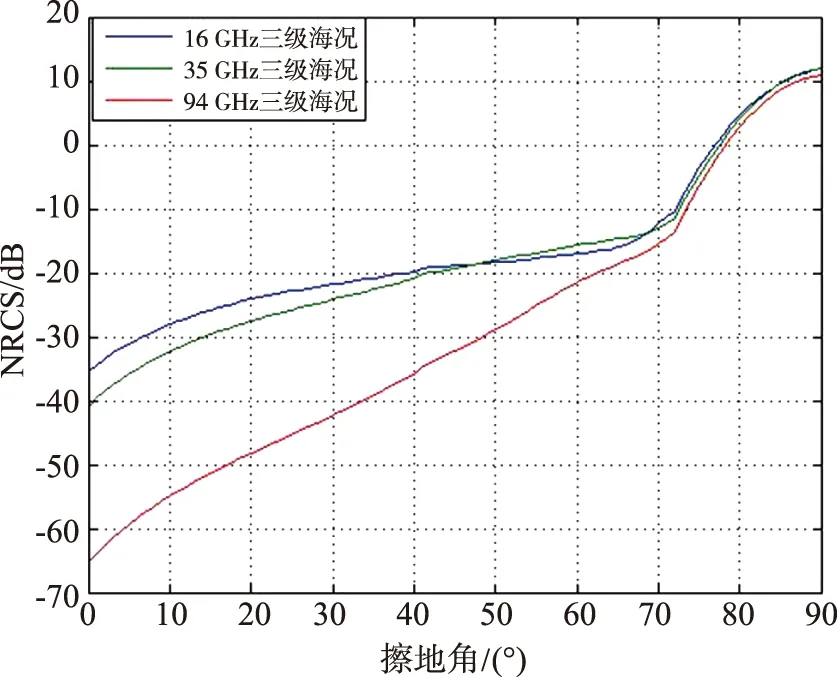
图1 散射系数与擦地角的一般规律Fig.1 General relationship between scattering coefficient and ground-rubbing angle

在每个区，散射系数与擦地角的关系可以用一定的散射机制解释。在准镜面反射区，电磁波接近垂直入射，散射能力以相干镜面反射为主，散射系数随擦地角减小而迅速下降，该区的宽度和斜率主要取决于地海面的大尺度特性。在平坦区，粗糙面的非相干散射机制占据主导，散射系数随擦地角的变化较为平缓。在近掠射区，擦地角小，由于遮挡效应和多路径干涉效应，散射系数随擦地角变化情况复杂，整体表现为快速下降趋势。

3个区的界限划分并不十分明确，可能会出现一定程度的交叉，特殊情况下还需要考虑全反射和布鲁斯特效应。

2.2 几个典型后向散射系数模型

地面散射系数模型的建立，通常是在开展地面散射特性测量的基础上，对大量测量数据进行统计分析才能完成。由于这些模型来源于大量测量结果的积累，通常又称之为地面散射系数经验模型。

目前，国内外不同学者和机构在大量测量数据的基础上建立了一些典型的模型，主要包括修正的等r模型[8]、r-f模型[8]、Morchin模型[9-10]、Kulemin模型[11]、GIT (georgia institutes of technology)模型[12]、Ulaby模型[4]等。

2.2.1 Morchin模型

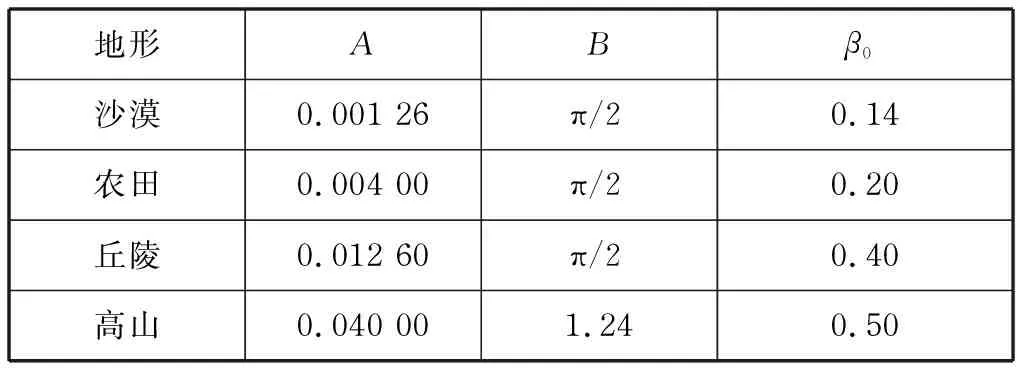
表1 Morchin模型不同地形类参数Tab.1 Different terrain class parameters of Morchin Model

2.2.2 Kulemin经验模型

式中：f为频率，单位为GHz；φ为擦地角，单位为°；系数A、B、C随地面目标不同而不同。通常也采用最小二乘拟合方法对Kulemin经验模型中的参数进行确定，将A、B、C作为待定系数，输入测量的入射角和后向散射系数，得到一个超定方程组，利用最小二乘法求解该超定方程组，便可以获得A、B、C的解。

该模型适用于频率在3～100 GHz范围内、擦地角小于30°、各种地面粗糙度的情况，其局限性在于只适用于掠入射情况。

2.2.3 Ulaby经验模型

σ0=A+Be-C θ+Dcos(Eθ+F)

式中：θ为入射角，单位为rad；A、B、C、D、E、F需通过拟合实验数据确定，其求解方法同2.2.2所述。

Ulaby经验模型涵盖了9种常见的地物类型(包括树木、草地、灌木、矮小植被、路面、城市、裸土、干雪、湿雪等)，涵盖L、S、C、X、Ku、Ka、W七个频段，其入射角适用范围为0°～80°。其局限性主要在于，对于每种地物需要用大量的测量数据进行非线性拟合才能获得较为准确的散射系数模型，同时对于我国西北地区广漠的沙漠、戈壁、冻土等地物类型适应性较差。

因此，后续需根据模型中不同类型地物中缺失的频段、擦地角(如对于树木，只有X和Ku频段数据)开展大量补充实验，完善模型的适用范围。同时开展高分辨、大动态条件下的杂波测量，提高模型适用的工作条件。

2.2.4 GIT模型

式中：δ是表面标准差，单位是cm，与地形种类等因素有关；A、B、C、D是根据经验获得的常数，与雷达频率、地形种类有关；θ为擦地角，单位是rad。其中，常数C的引入是为了更精确地模拟实验数据并防止在擦地角接近0°时用分贝表示的σ0急剧变为-∞。

该模型适用于频率3～95 GHz、擦地角在5°～70°范围内散射系数的建模，其局限性在于只适用于干燥地面，对于潮湿地面，所给出的散射系数偏低，且没有考虑极化的影响。

上述4种模型的适用范围广泛，且经过较多的实验验证，可信度相对较高。但是目前还没有关于其模型置信度评价的相关研究，后期需建立一套完备的散射系数置信度评价模型，对于各类输入参数、各类使用条件都给出定量的置信度描述，更好地指导雷达探测系统的设计。

3 杂波概率密度函数分布

有关描述杂波后向散射系数的概率密度函数的分布模型，比较公认的幅度概率密度函数分布模型为Rayleigh分布、LogNormal、Weibull分布、K分布[1,13]等。

3.1 Rayleigh分布

式中：x为杂波幅度；σ为瑞利参数。该模型适于描述一个杂波分辨单元内有许多互相独立、无强散射源情况下的杂波，主要用于描述箔条干扰、气象杂波和低分辨率的雷达地杂波等。

3.2 LogNormal分布

式中：x为杂波幅度；σc为形状参数，一般取值σc=0.355～1.147；μc为尺度参数，一般取值σc=0.5～1.2，两者分别用于描述分布的偏斜度和中位数。该模型适于描述高分辨率情况下平坦地形或低入射角情况下复杂地形的雷达杂波。

3.3 Weibull分布

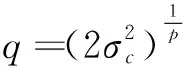
3.4 K分布

式中：x为杂波幅度；a为标度参数，只与杂波均值相关；v为形状参数，取值范围v>0.1。当v→0.1时，K分布具有显著峰值，意味着尖峰杂波；当v→+∞时，K分布趋于瑞利分布；v取值在0.1～3之间时，该模型适于描述低擦地角、高分辨率情况下的海杂波。Kv-1是修正的v-1阶贝塞尔函数，Γ(v)为伽马函数。K分布适于描述高分辨率雷达非均匀杂波，常用于海杂波模拟。

4 杂波功率谱

4.1 常用杂波功率谱模型

雷达杂波幅度的概率密度分布模型描述了杂波信号在时域的一维表示，通常要更好地描述杂波的分布特性，还要描述杂波频域的二维分布特性，这就是杂波的频谱分布模型。雷达杂波的频谱常用以下3种模型表示。

1) Gaussian谱模型

式中，σf为杂波谱的标准差。

2) Cauchy谱模型

式中，fc为截止频率，在该频率处信号幅度下降3dB。

3) AllPole谱模型

其中：fc为截止频率；n的典型值为2～5。

4.2 满足特定功率谱的杂波仿真计算

根据上述统计模型，首先给出了几种地形的后向散射系数及杂波序列的仿真结果，然后仿真生成满足特性功率谱的杂波相关随机序列。

4.2.1 归一化后向散射系数

以Morchin模型对沙漠、农田、丘陵和高山等典型地形进行计算，获得其归一化后向散射系数随频率和入射角的变化关系，如图2所示。

图2 不同地形的NRCS与入射角和频率的关系Fig.2 Relationship between NRCS of different terrain and incidence angle and frequency

由图2可以看出：①随着入射角增加(擦地角减小)，沙漠、农田和丘陵地形的归一化平均后向散射系数均降低，高山的归一化平均后向散射系数先略微升高再降低，这主要是由于高山本身存在一定的角度；②在低入射角时，沙漠和农田后向散射系数高于丘陵和高山后向散射系数，这主要是由于沙漠和农田相对平缓，接近垂直入射，而丘陵和高山存在一定的角度，偏离垂直入射；③高入射角时，高山的后向散射系数最高；④后向散射系数在20°～80°入射角范围内变化相对平缓，这一区域通常被称为过渡区。

4.2.2 相关杂波序列仿真

当雷达照射地面场景时，观测某个距离单元的回波在慢时间上的变化情况，即便雷达与地面观测关系不变，所得的回波也是随时间起伏的。这是由于单个杂波距离单元内部含有大量散射体且散射体之间存在相对运动，导致其后向散射系数起伏。

事实上场景的后向散射系数时刻在变化，为了简化，我们借鉴雷达中的“停-跳”模型，认为在单个脉冲重复周期内场景后向散射系数保持恒定。到下一个脉冲发生时刻，场景后向散射系数突变。场景后向散射系数的相关起伏导致杂波的相关起伏。

目前，仿真生成相关随机序列的方法主要有两种：零记忆非线性变换(zero memory nonlinear, ZMNL)和球不变随机过程(spherically invariant random process, SIRP)[13]。这两种方法较为成熟，此处不做展开。本文给出以ZMNL法生成具有高斯谱的相关LogNormal分布杂波序列。

设雷达脉冲重复周期fr=1 000 Hz，共发射2 000个脉冲，杂波服从LogNormal分布，具有高斯谱相关性。仿真所得的杂波序列如图3所示。

图3 具有高斯谱的相关LogNormal分布杂波序列Fig.3 The coherent LogNormal distribution clutter sequence with Gaussian spectrum

从图3中可以看出，仿真所得杂波序列的概率密度函数和功率谱与理论情况吻合较好。

5 对地海杂波统计建模发展的一些思考

国内外学者和研究机构对地海杂波统计特性开展了大量的研究工作，研究成果推动着雷达性能的持续提高。当前，地海杂波特性研究方面还存在以下问题。

1) 模型研究得多，置信度研究得少，模型适应性差，使用盲目

现有模型主要依赖于测量数据，而测量数据受限于实验条件存在数据不足、针对性强、普适性差的问题，适用于小擦地角多、大擦地角少，低海情多、高海情少，低频段多、高频段少的场景。模型输入参数多，参数取值标准不统一，取值范围大，由此造成使用的盲目性。研究模型种类多，置信度低，模型适用性情况复杂，造成对模型的选择困难。

地面基本元素构成复杂，地形地物类型繁多，人造散射体和人为地表活动日渐增加，同时描述地表环境特性的参数极多，即便是同种类型的地表其含水量、含盐度、温度等等都完全不一样。而海面状态随气象条件千变万化，描述海面的环境参数也较多，且影响海杂波强度的雷达系统参数与海洋环境参数之间存在着复杂的非线性依赖关系。测量系统方面，船载、车载测量系统很难实现大擦地角的测量，而高海况的机载、船载测量危险性较大。因此，想要完备地获得所有地表类型、海情海况、频段、擦地角和极化的测量数据是一个不可能完成的任务，想要通过测量手段准确建立地海面散射系数模型难度很大。

测量数据不足导致模型的建立往往仅采用部分波段下的数据，模型在其他波段下的适用情况存在不确定性，对模型的正确性校验也不可能面面俱到，因此必须持续开展杂波测量工作以及高置信度的杂波仿真建模工作。同时，需开展杂波统计模型置信度评价方法研究，对所输出的结果进行定量的置信度评价。

模型中的输入参数较多，且标准不统一，输入条件可变范围大，这将导致模型使用者的盲目性，造成人为的失误。该问题可通过基于人工智能的杂波参数自适应调整来实现，根据实际测量的环境参数、拍摄的环境照片，由深度神经网络确定杂波统计模型的输入参数。

随着人们对雷达技术应用的不断认识，发现双基探测在某些方面具有比单基探测更大的优势，而双基探测需要对杂波的双站特性进行研究，目前还未开展相关工作。

2) 表达式研究得多，分布参数研究得少

当前，对于地杂波散射系数、幅度分布的研究多集中于其分布的函数形式上，而对于每种概率密度函数(probability density function, PDF)分布参数的确定方法研究较少。目前主要的研究内容都是根据实测地海杂波数据并采用最大似然估计或矩估计的方法拟合分布参数，而对于分布参数与地表类型、海情海况、地海面环境参数、雷达参数的关系研究较少。因此，通常难以从地海面环境特性和雷达参数直接推算得到全部的PDF信息，必须加强分布参数建模研究。

3) 时间相关性研究得多，空间相关性研究得少

合成孔径雷达(synthetic aperture radar, SAR)成像体制更关注空间相关性；缺乏对海杂波空间相关性的了解，将导致雷达目标恒虚警率(constant false-alarm rate, CFAR)检测时单元平均数选取盲目，从而无法获取最优化的CFAR增益，使目标检测性能下降。因此，必须加强空间相关性及时空二维相关性建模研究。

4) 传统参数拟合方法难以适应大数据

杂波模型参数拟合需要大量的实测数据，这样所获取的模型才具备更广泛的适用性。但是采用传统的最小二乘方法对模型参数进行拟合时，若需要确定的参数与输入的测量数据过多，会出现拟合失败的情况。这主要是由地杂波的复杂性导致的。通常进行参数拟合时，需要按照频段、地物类型等区分大类(如X频段的草地)，然后针对此种条件下的测量数据进行参数拟合，因此在使用时也局限于X频段的草地，外推能力不足。随着人工智能技术的不断发展与测量数据的不断积累，将深度神经网络用于地杂波建模具备可实施性。将各种地物、频段、测量条件下的数据进行标注后，输入深度神经网络进行训练学习，可以得到适用范围更加广泛的杂波统计模型，同时可以实现杂波模型置信度的定量评价。

6 结束语

本文在总结常用的3类描述地海杂波的经典统计模型的基础上，给出了常见地形、不同频率、不同入射角的平均后向散射系数，并给出了满足特定概率密度函数和功率谱的杂波仿真方法和结果。并且，针对当前地海杂波特性研究的现状，给出了若干关于地海杂波统计建模研究方面的思考，指出地海杂波建模在置信度评价、适应性提升、分布参数建模和大量实测数据分析方面需要开展进一步的工作。